施工中对预应力张拉伸长量计算的分析

林 汛

(广东冠粤路桥有限公司，广东 广州 511400)

0 引 言

预应力钢束的出现显著提升了梁体结构刚度进而突破了钢筋混凝土桥梁的跨度瓶颈,因而被广泛应用在高速发展的铁路、高速公路工程中[1]。合理的施工张拉工艺可以保证预应力混凝土梁良好的结构性能和可靠的耐久性。为了减少预应力损失带来的施工误差,预应力张拉目前主要采用“以张拉力为主,伸长值为辅”的双控方法,且规范明确要求实际伸长值与理论伸长值误差不得超过6%,准确计算张拉理论伸长值是预应力筋张拉施工前最重要的步骤[2-6]。

高速公路桥梁中预应力钢束应用已是非常普遍,本人根据多年高速公路桥梁施工经验,以及实际施工生产中碰到的问题,结合现场施工案例,通过对预应力钢绞线非对称性张拉及弯桥内外侧张拉两端伸长值的计算实例,剖析了既有设计方法的计算缺陷,并给出考虑最小平衡力分界面的伸长值计算方法,以期对现场施工有所帮助。

1 理论伸长量计算机制

后张法预应力钢绞线的理论伸长值ΔL的计算公式为[7-9]:

式中:ΔL为各分段预应力筋的理论伸长值,mm;Pp为各分段预应力的平均张拉力,N;L为预应力筋的分段长度,mm;AP为预应力筋的截面面积,mm2;Ep为预应力筋的弹性模量,N/mm2。

其中：

式中:P为预应力筋张拉端的张拉力,将钢绞线分段计算后,为每分段的起点张拉力,即为前段的终点张拉力,N;x为从张拉端至计算截面的孔道长度;θ为从张拉端至计算截面曲线孔道部分切线的夹角之和,分段后为每分段中每段曲线段的切线夹角,rad;k为孔道每米局部偏差对摩擦的影响系数;μ为预应力筋与孔道壁之间的摩擦系数,只在弯曲管道部分考虑该系数的影响。

2 纵桥向预应力钢束非对称性两端张拉情况

桥梁设计中经常遇到因桥梁跨径结构非对称性以及梁板结构未对称性,产生的非对称张拉。为了简化计算,一般在结构中间截面取分界点,分段计算伸长量,计算出两端不同伸长量。然而非对称钢绞线的受力平衡点通常不在中心,理论上应分析两个方向拉力的最小平衡界面,并以此分界面为基准,分别计算两端分非对称伸长量。两个方向拉力的平衡截面分析计算时,先根据经验假定钢绞线某一点为受力平衡分界点,建立平衡方程,并经过多次试算找出最终平衡点。笔者在实际施工中就碰到了多个纵桥向预应力非对称性张拉案例，如云湛高速TJ28合同段樟檬枢纽互通C匝道桥第三联现浇箱梁25m+2×30m+27m组合结构预应力混凝土连续箱梁，清云高速TJ2合同段40m T型梁,对施工过程中产生的问题进行复核、协调解决。下面以40m T型梁实例进行阐述。

清云高速公路TJ2合同段,三坑河大桥采用40m T型梁+25m小箱梁组合结构,40m T型梁为先简支后连续结构,预应力筋弹性模量为Ep=1.95×105MPa,松弛系数0.3,锚具变形、钢筋回缩按6 mm(一端)计算,金属波纹管摩阻系数为0.25,偏差系数为0.001 5。以边跨钢束N1为例,钢束构造如图1所示,借助Excel分别从伸缩缝端和连续端计算各钢束段始末张拉力、平均张拉力及伸长值,将上一节段的终点张拉力作为下一节段的初始张拉力,依次计算并寻求最小应力平衡点,其预应力张拉计算见表1。

图1 钢束布置图

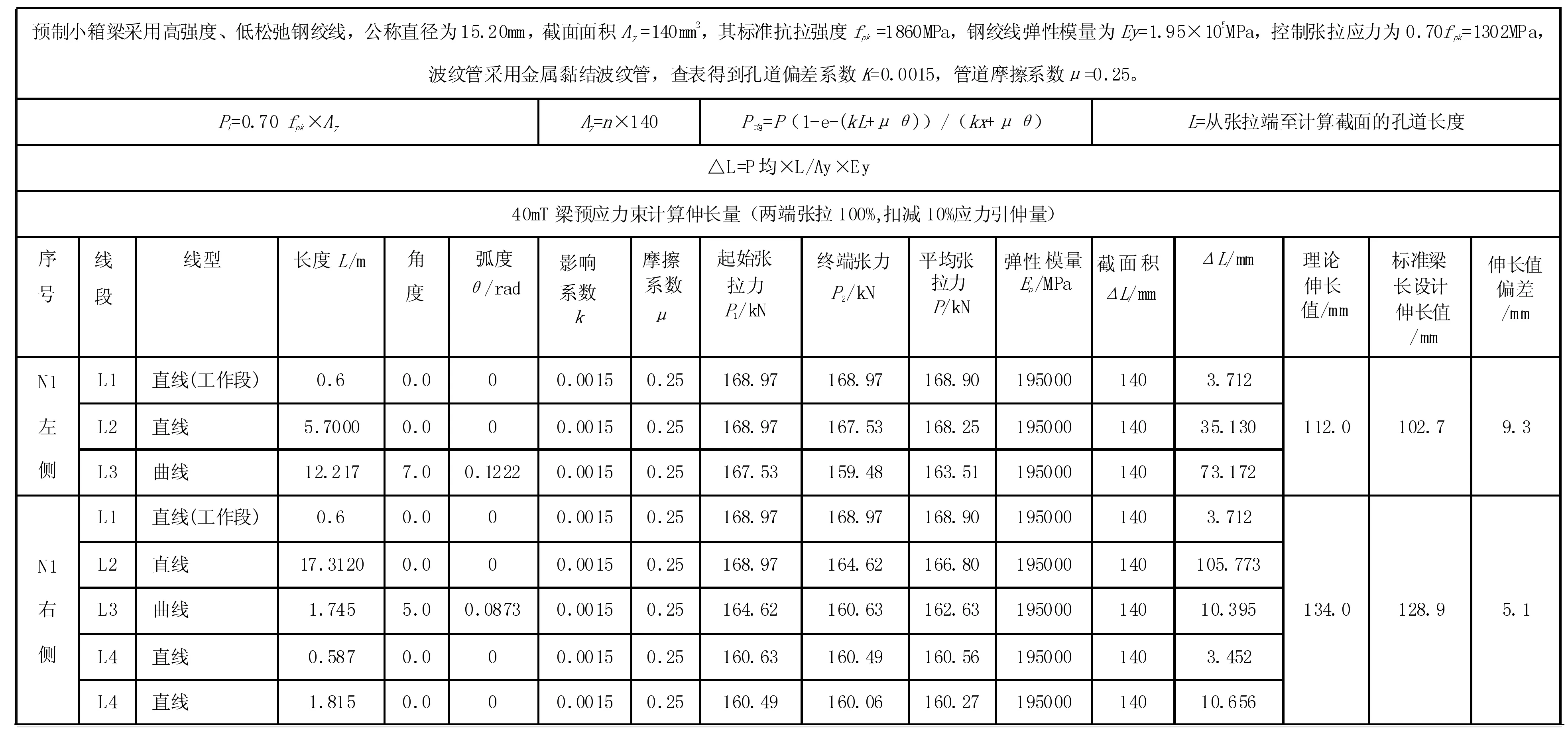
表1 非对称张拉预应力伸长量计算表

计算过程如下:将既有钢束分为8段,并拟定其最小平衡力截面位于L1.815左处。若L12.217右和L1.815左最大值在终点力最小值段的初始和终点张拉力范围内,则可确定最小平衡力位置位于该段范围内,进而基于黄金分割法确定其具体最小平衡力位置;反之,则需要调整拟定最小平衡力位置,并重新进行判断直至找到最终最小平衡力位置。

根据表1可知,L12.217右=159.48 kN,L1.815左=160.06 kN,相对偏差仅为0.4%,偏差率较小并不影响伸长量计算,因此可以确定拟定截面即为最小平衡力截面。

将理论值和设计值对比发现,非对称张拉两端伸长量理论值较设计值偏大,伸缩端伸长值偏差为9.3mm,偏差率为9.1%,已经超出桥梁施工规范要求的6%,而连续端伸长值偏差5.4,偏差率为4.2%。相比于管道摩阻系数、锚垫板预埋位置、千斤顶配套等其他问题引起的累积误差,未考虑对称张拉所带来的误差更加容易解决,进而提高伸长量的校核精准度。

3 平面横桥方向预应力钢束非对称性张拉情况

平弯出现在匝道现浇箱梁居多,匝道桥现浇箱梁一般位于平曲线上,内外半径差异较大,其内外侧钢束平弯必然有一定的区别[10],设计时为简化工作一般以桥梁设计中心线钢绞线提供平均伸长量,而忽略考虑平曲线内外差异带来的影响。

笔者接触过匝道桥梁较多,在云湛高速TJ28合同段樟檬枢纽互通C匝道桥第三联现浇箱梁中,发现由于道路平曲线的存在,其内外侧伸长量存在约5mm的差值,这对小半径大跨度桥梁影响尤其明显。同时笔者也发现,由于平弯带来的横桥向非对称张拉的影响与桥梁半径和桥梁宽度有着密切的关系,桥梁平弯半径越小,桥梁越宽,其非对称张拉效应越明显,设计时更应该给出内外侧相应的伸长量以便于更好地校核张拉力,而不是仅仅给出结构中线对应的伸长量。

4 结束语

在纵向预应力钢绞线伸长值的计算中,建议设计时结合预应力钢束的实际线型特征和张拉方式,基于分段计算原则判断最小平衡力位置。进而计算出相应段预应力钢绞线的始终点截面拉力、各分段长度的平均拉力,这样计算出更为精确的理论伸长值,以期更好地指导预应力张拉工序。

针对平弯半径带来的内外侧钢束伸长值的差异亦不能忽视,尤其对于小半径大跨度桥梁,设计时应给出同号钢束内外侧的不同伸长量值。既可以避免由于半径带来的张拉误差,又可以方便施工时对设计值进行二次复核。

伸长值的准确计算既能校核张拉施工的可靠性,也能针对实际施工时的偏差及时纠偏,从源头上保证预应力张拉施工的质量。