基于速度标准差系数的城市地下互通合流区交通安全评价研究

王 红, 田 龙, 陈 勇

(武汉理工大学，湖北 武汉 430063)

0 引 言

随着城市交通的快速发展，地面交通已经渐渐饱和，为了满足日益增长的交通需求，在城市核心区建设地下道路是缓解城市交通拥堵的有效措施[1]。其中地下互通合流区是地下互通立交的重要组成部分，改善合流区交通安全状况，能有效提高地下互通立交的通行能力，保障地下互通立交综合功能。

目前，地下道路交通研究主要集中于道路交通设计及场景模拟实验[2,3]。对于地下道路交通设计，主要针对道路、桥梁、隧道等安全设计和施工方法的安全评价，通过建立指标体系，采用安全检查表(SCL)法、危险度评价法、影响性分析(FMEZ)等定性评价和事故树分析(FTA)、模糊数学综合评价和层次分析法等评价方法优化道路安全设计[4,5]，较少涉及城市地下道路相关研究。随着城市地下道路的建设与发展，研究者对城市地下快速路出入口布置及地下道路合流区驾驶员视认行为展开研究[6,7]。吴义虎等[8]通过考虑车辆平均车速、车速标准差对路段事故率的影响机制，发现路段事故率与车速离散性的相关系数最大，影响路段交通安全的主要因素是车速分散性。裴玉龙等[9]建立的亿车公里事故率与速度标准差的关系模型。这些都说明地下道路交通是研究热点，但现阶段关于城市地下道路关键节点，如地下互通，研究却较少。而地下互通合流区作为关键节点的重要组成部分，对其进行安全性评价具有重要意义。因此，本文在获取厦门万石山地下互通立交的隧道内主线出入口、分合流点监控视频、近5年事故数以及实验车实测数据所构建得地下互通立交合流区仿真模型的前提下，选定速度标准差系数作为合流区安全评价的指标，对地下互通合流区安全性进行分级，通过对合流区不同区段进行安全评价，提升地下道路合流区安全水平。研究结果可为地下道路工程设计提供参考。

1 速度标准差系数与影响因素关系模型

速度标准差系数又称速度均方差系数，是反映速度变动程度的相对指标，其计算公式为:

(1)

一般情况下，对于不同水平的总体不宜直接用速度标准差指标进行对比，速度标准差系数能更好地反映不同水平总体的速度变动度。

1.1 影响因素的相关性分析

1.1.1 加速车道点位百分比

对于合流区，一般设置加速车道，不同交通条件下加速车道长度不同。为研究加速车道区域不同点位的速度分布情况，将整个加速车道长度分为5等份，相对合流鼻端位置构成5点位。定义点位百分比，即点位距离合流鼻端长度占加速车道总长度的百分比。点位百分比可以更好地分区域来研究合流区交通流特性，体现出各断面间的差异性，所以建立速度标准差系数与点位百分比的关系，分区域评价合流区的安全性，每个点位占比分布为0.2、0.4、0.6、0.8、1。通过分析，各点位百分比与速度标准差系统关系如图1所示。

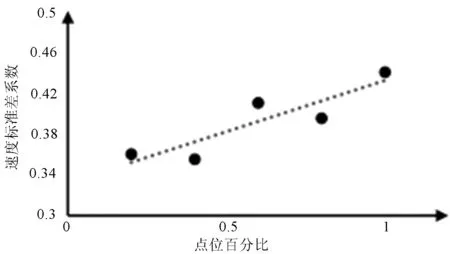
图1 速度标准差系数与点位百分比关系

由图1可知，随着点位百分比的增大，即与合流鼻端的距离越大，速度标准差系数越大，这说明，合流区后半部分的车速离散性大，合流行为使主线和加速车道的车速都产生很大变化，而且数据都分布在趋势线附近，点位百分比与速度标准差系数相关性较强。

1.1.2 主线交通量

速度标准差系数与主线交通量关系如图2所示。

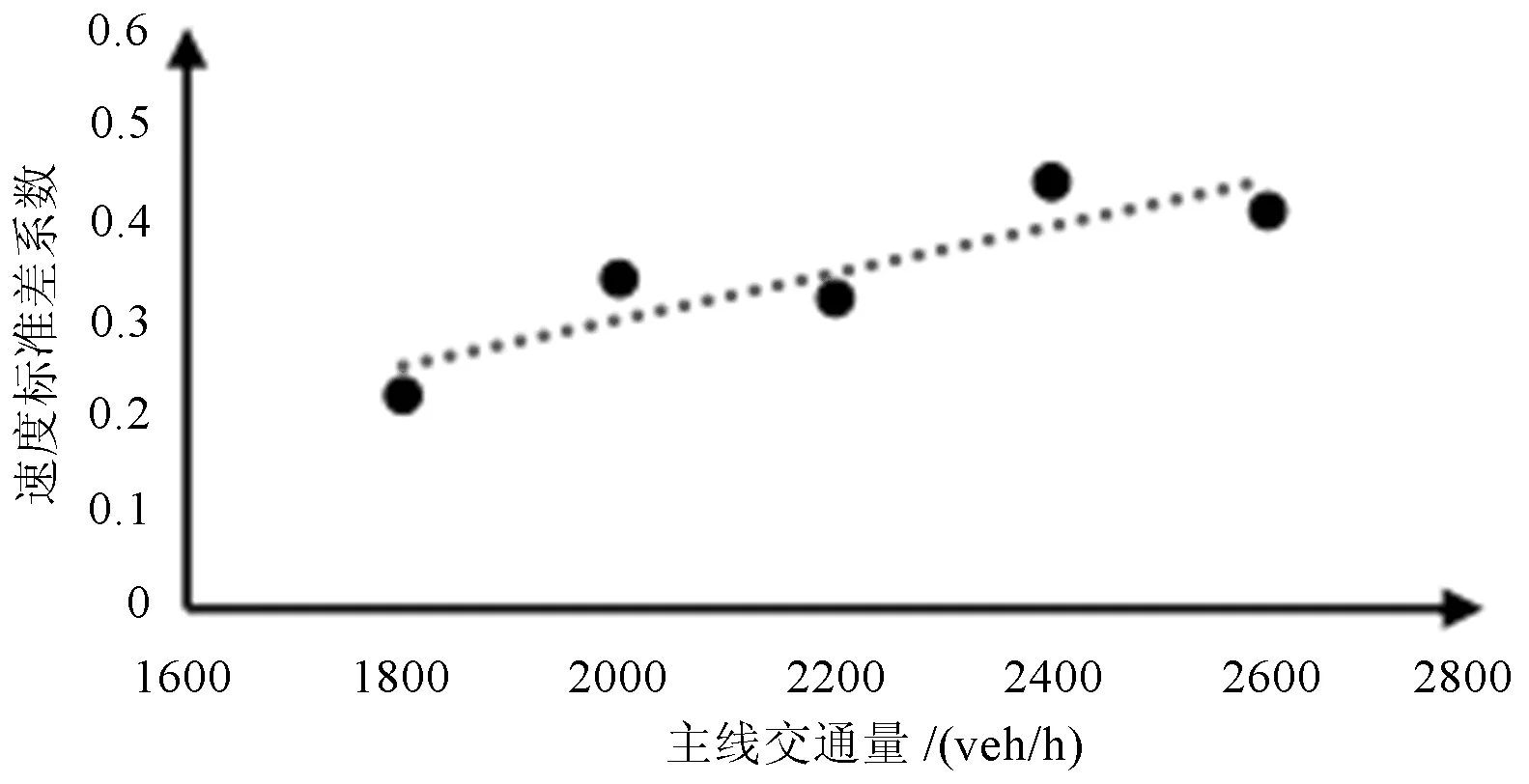
图2 速度标准差系数与主线交通量关系

由图2可知，主线交通量增加，速度标准差系数也增大。因为主线交通量较小时，加速车道车辆可以自由汇入主路，不用过多考虑合流对主线车辆造成的影响，两者的速度都比较稳定。当主线交通量增大时，最外侧车道不断高速驶过的车辆会干扰到想要合流的车辆，使速度标准差系数都变大。而且数据都分布在趋势线附近，主线交通量与速度标准差系数相关性较强。

1.1.3 大车混入率

速度标准差系数与大车混入率关系如图3所示。

图3 速度标准差系数与大车混入率关系

从图3可知，随着大车混入率的增大，速度标准差系数显著提升，这是因为大型车的加减速性能较差，质量较大，在合流区这个交通复杂的位置难以即时改变自身的速度以适应速度不同的各方向车流，速度标准差系数增大，从整体来看，实验点分布紧密，相关性较强。

1.1.4 匝道交通量

速度标准差系数与匝道交通量关系如图4所示。

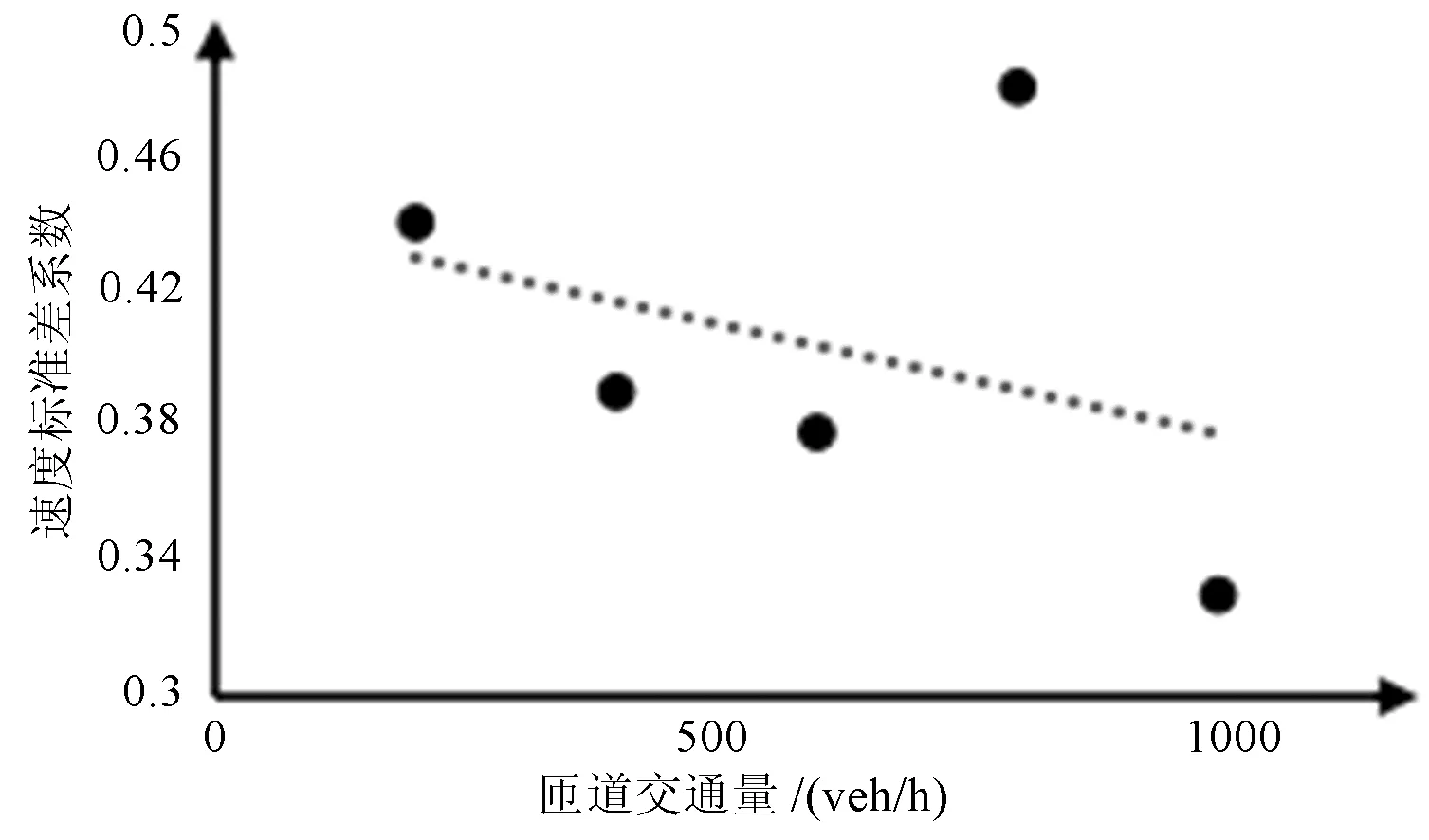
图4 速度标准差系数与匝道交通量关系

由图4可知，匝道交通量增大，速度标准差系数总体上是减小的，原因之一是随着匝道交通量的增大，需要汇入主路的车辆也逐渐变多，会导致主线最外侧车道以及加速车道上的车流发生阻塞甚至暂时停滞，断面间速度差异反而减小，并且有两组数据距离趋势线很远，整体分布离散，两者相关性很弱。

1.1.5 匝道设计车速

速度标准差系数与匝道设计车速关系如图5所示。

图5 速度标准差系数与匝道交通量关系

由图5可知，匝道设计车速增大，速度标准差系数会减小。这个现象是因为匝道设计车速越高，从匝道驶出的车辆行驶速度也越高，加速到与主线车速相同的速度只需要较短的距离，没有充分加速就强行汇入主路的车辆会变少，降低了车速的差异程度。而且图中数据分布较为离散，初步认定两者相关性不强。

以上初步分析了加速车道点位百分比、主线交通量、大车混入率、匝道交通量、匝道设计车速5个影响因素与速度标准差系数间的关系。并得出结论：加速车道点位百分比、主线交通量和大车混入率与速度标准差系数关系显著，匝道交通量和匝道设计车速与速度标准差系数关系不显著。利用SPSS 24.0软件相关性分析方法中的双变量命令，确定速度标准差系数与各道路条件和交通条件因素是否具有统计学层面的意义，验证以速度标准差系数为因变量，加速车道点位百分比、主线交通量、大车混入率、匝道交通量和匝道设计车速为自变量构建模型可行性，分析结果见表1。

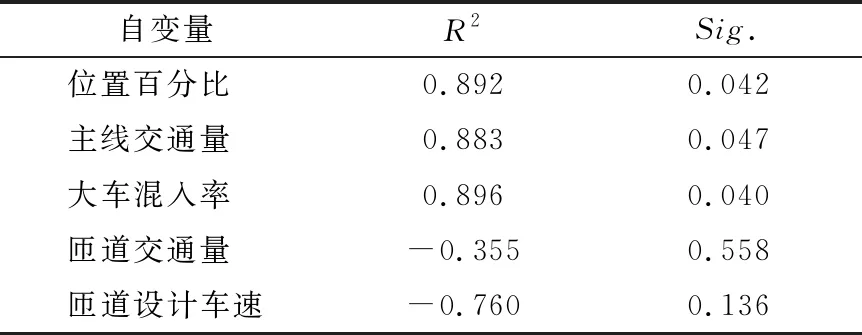
表1 标准差系数与影响因素相关性分析

在相关性分析理论中，在置信度为95%的前提下，如果可以得出两组数据的显著性Sig.小于0.05，同时相关系数R2大于0.8，说明这两组数据相关性极强。据此，分析表1中数据可知，只有匝道交通量和匝道设计车速的Sig.大于0.05，且R2小于0.8，而位置百分比、主线交通量、大车混入率均符合评判是否相关的要求，所以，有充分理由选取位置百分比、主线交通量、大车混入率作为交通安全评价模型中的自变量。

1.2 速度标准差系数模型构建

在模型仿真结果中，整理出自变量位置百分比、主线交通量、大车混入率变化时对应的速度标准差系数，输入SPSS 24.0，调用回归命令，将自变量和因变量正确对应，运行后得出如下交通流影响因素与安全评价指标速度标准差系数的模型。

Cv=0.06+0.31P+0.0000003Qz+0.624PHV

(2)

式中：Cv为合流区某区域的速度标准差系数；P为合流区某区域的位置百分比；Qz为合流区主线交通流量,veh/h；PHV为大车比例。

构建出了地下互通立交合流区速度标准差系数模型之后，还需要对模型的有效性进行检验。

(1)显著性检验。利用SPSS 24.0在置信度为95%的前提下对仿真模型进行检验，结果见表2。

表2 显著性检验结果

分析表2中数据得出，在F检验和t检验下的显著性水平Sig.均小于0.05，说明在位置百分比、主线交通量、大车混入率等共同作用下，速度标准差系数受到的影响是显著的，三个自变量分别单独作用于速度标准差系数的影响也是显著的，这充分说明构建的模型具有统计学意义。

(2)有效性验证。将实测数据(点位百分比、主线交通量及大车混入率),代入构建出的模型(2)中，计算出相应的速度标准差系数并与通过实际调查获取的速度标准差系数进行对比，结果统计见表3、表4。

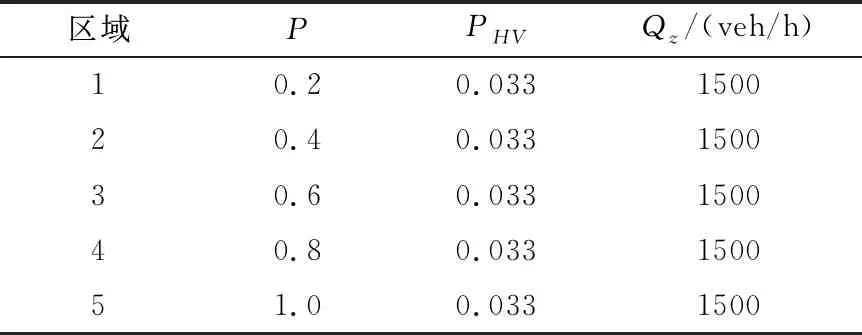
表3 模型自变量取值

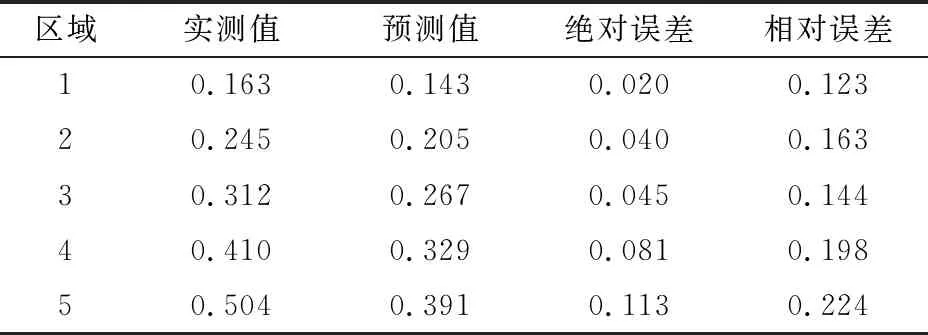
表4 速度标准差系数预测值与实测值对比

分析表4中数据，只有第五组数据的预测值与实测值间的相对误差稍大，为0.224，准确性低于80%，其余4组数据相对误差很小，准确性几乎都在80%以上，预测值总体上符合实测值的变化趋势。因此本章以速度标准差系数为因变量，加速车道长度、主线交通量和大车混入率为自变量构建的模型是有效的。

2 交通安全等级划分

2.1 速度标准差系数与交通安全

体现交通安全性最直观、最准确的指标是事故率，此次收集了厦门万石山地下互通立交近5年的事故资料，记录了事故类型、事故发生时间以及大致的事故发生地点，但无法获取事故发生时本身的车速以及合流区域的车速情况，无法分析事故与速度标准差系数的关系，所以借鉴已有的相关研究。裴玉龙等[9]通过收集我国部分高速公路的交通流和事故数据，建立了亿车公里事故率与速度标准差的关系模型。借助于其研究得到的数据，先将某个事故率对应的速度标准差转化为速度标准差系数，绘制出两者的散点图,如图6所示。

图6 速度标准差系数与亿车公里事故率关系

采用回归分析方法，得到如下亿车公里事故率与速度标准差系数关系模型。

AR=6.2424e10.231Cv

(3)

式中：AR为亿车公里事故率；Cv为速度标准差系数。

2.2 地下互通立交合流区交通安全的等级划分

上节已经建立了事故率与表征交通流安全性的指标速度标准差系数的关系模型，本节将对地下互通立交合流区进行交通安全评价。区分合流区不同区域交通安全性大小的核心问题是分界点的确定。确定分界点常用的方法是以15%和85%位值来区分，如限速方案的制定也是以行驶速度累计频率的15%和85%位值为划分标准[10]，本文采用相同方法确定事故率的分界阈值。

陈晓冬等[11]收集了长平高速公路上大量的交通流数据和事故数据，借鉴文中的事故数据，绘制了事故率累计频率曲线，如图7所示。

图7 事故率累积频率曲线

根据曲线走势，当累计频率为15%时，对应的事故率是32(次/亿车公里)，当累计频率为85%时，对应的事故率是61(次/亿车公里)。将上述两个事故率的值代入关系模型(2)，得到对应的速度标准差系数阈值分别为0.160与0.223，以此为依据将合流区划分为三个安全等级，具体划分见表5。

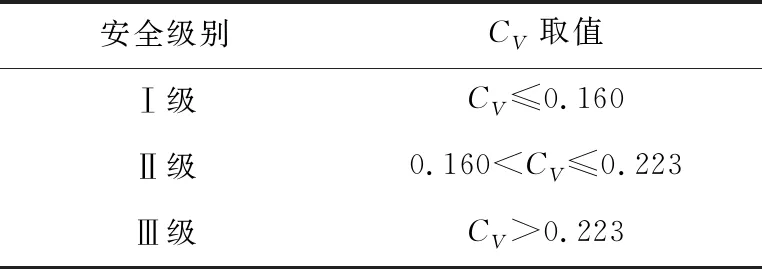
表5 基于CV值的合流区安全评价等级

Ⅰ级：速度标准差系数值很小，速度分布离散性很小，交通流运行稳定，发生事故的概率很小，安全水平较高。

Ⅱ级：速度标准差系数值较大，速度分布离散性也随之增大，车辆间的相互干扰现象增多，交通流的稳定性下降，发生事故的概率上升，安全水平下降。

Ⅲ级：速度标准差系数值过大，速度分布离散性太大，不同速度的车辆相互干扰严重，交通流运行混乱，容易发生事故，安全水平很低。

城市地下互通合流区区段安全性可以体现地下互通合流区交通安全性，在安全性较低的区段，应当采取措施，降低车辆的速度离散程度，提高合流区安全性。

3 结束语

本文采用速度标准差系数对合流区交通安全进行评价分析，通过分析速度标准差系数与加速车道点位百分比、主线交通量、大车混入率、匝道交通量、匝道设计车速的相关性，以点位百分比、主线交通量、大车混入率为自变量，速度标准差系数为因变量进行回归分析，建立对应模型。借鉴已有研究，建立速度标准差系数与事故率的函数关系，并以事故率累计频率15%和85%位值为分界阈值，计算出了速度标准差系数的分界阈值为0.160和0.223，得出如下标准：当Cv≤0.160时，安全等级为Ⅰ级；当0.1600.223时，合流区安全等级为Ⅲ级。本文将地下互通立交合流区分为三个安全等级，对其进行安全评价，研究结论可为相关工程建设和设计提供参考。