基于GPR的PC连续梁桥体系可靠度分析

黎恩华, 陈忠宇, 毛 林

(武汉理工大学 交通学院，湖北 武汉 430063)

0 引 言

桥梁可靠度分析是桥梁工程领域中的重要研究方向。桥梁与其他结构形式相比,其复杂的结构形式伴随着多失效模式导致其功能函数往往呈高度非线性并且没有确切的解析表达式。隐式的功能函数使得常用于求解可靠度的一次二阶矩法无法对其求导从而难以解决问题。如何将隐式功能函数显式化是解决问题的关键,响应面方法(RSM)的出现促进了问题的解决,但是响应面方法在处理非线性较强隐式功能函数时,响应面函数难以精确拟合真实功能函数,计算误差较大。蒙特卡罗模拟法(MCS)求解此类可靠度问题计算精度较高,但由于其计算所需的抽样次数较大导致效率较差。随着机器学习理论的发展,结构可靠度领域开始将人工神经网络(ANN)、支持向量机(SVM)[1]等方法引入并取得了不错的研究成果。但上述响应面方法尚存在着不足之处，如ANN在小样本条件下学习预测能力差以及容易出现过拟合,而SVR则存在损失函数和超参数难以确定的理论问题。

与ANN、SVR等回归模型相比,高斯过程回归(GPR)具有超参数自适应、泛化能力强、预测结果具有相应的置信度结果等优点。本文提出一种将高度非线性函数回归的GPR方法与JC法相结合的体系可靠度计算方法，并将其应用于PC连续梁桥体系可靠度的求解。

1 基于GPR的可靠度计算方法

1.1 GPR基本理论

高斯过程最终的决策函数完全由均值函数和协方差函数确定[2]。

f(x)～GP(m(x),k(x,x′))

(1)

为了方便起见,通常在分析过程中将高斯过程的均值函数设为零。本文通过有限元模型分析得出响应值从而算出相应的功能函数值，属于计算机模拟试验,属于高斯过程中观察目标值无噪声的情况。假设训练样本为D=(X,y),其中X为训练样本个数和输入变量维数组成的m×n输入矩阵,y为结构真实响应值,则关于y的高斯先验分布为:

y～N(0,K(X,X))

(2)

式中，K(X,X)为m×m阶对称正定协方差矩阵,根据高斯分布先验概率可推得训练输出的联合分布为:

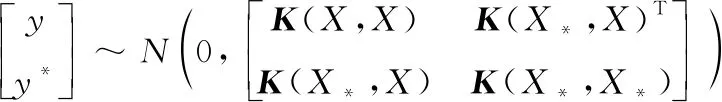
(3)

协方差函数选取为平方指数协方差函数,在不考虑噪声影响的情况下,其表达式为:

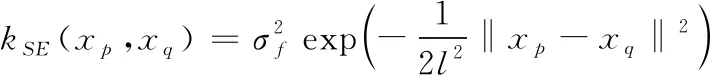
(4)

式中:σf为局部相关性的控制量;l为距离尺度。

通过学习样本数据得到的GPR模型的超参数对模型的精度而言至关重要,通常运用对数极大似然法和共轭梯度法相结合寻找最优超参数。对数似然函数具体形式如下:

(5)

根据贝叶斯原理,可推断出y*的预测后验分布均值为

(6)

式中:αi为α向量的元素;α=K-1y,k(xj,x*)为协方差矩阵K的列向量。

1.2 可靠指标高斯过程表达式

假设桥梁结构的极限状态方程为：

Z=g(x)=0

(7)

当选取桥梁随机变量x中存在非正态分布变量时,可通过一次二阶矩中的JC法将其转化为正态分布变量。采用GPR模型拟合该功能函数时,即：

(8)

(9)

桥梁可靠指标为：

(10)

1.3 可靠度计算流程

(1)采用拉丁超立方抽样(LHS)在样本区域(μi-3σi,μi+3σi)中抽取70组样本数据,其中50组为训练样本,20组为测试样本。

(2)将得到的样本数据作为GPR模型的输入,通过有限元分析软件得到对应的响应值,再根据失效限值求得功能函数值Z并将此作为GPR模型输出。

(3)采用高斯过程回归方法对训练样本数据进行学习。

(4)根据式(8)构建GPR模型将各个失效模式下的隐式极限状态方程显式化。

(5)采用JC法求解可靠指标。在式(10)的基础上,假定一个迭代点x*,重复迭代计算相应可靠度指标值直到最近两次的‖x*‖的差值小于允许误差,从而得到某个失效模式下的可靠指标。

基于上述可靠度计算流程编写相应的Matlab程序。

2 基于GPR桥梁体系可靠度计算

2.1 工程实例

长湖特大桥是位于湖北省荆州市跨越长湖的一座特大型桥梁工程,该桥主桥为四跨变截面预应力混凝土箱梁(30 m+2×50 m+30 m)。通过MIDAS Civil建立长湖特大桥有限元模型如图1所示。

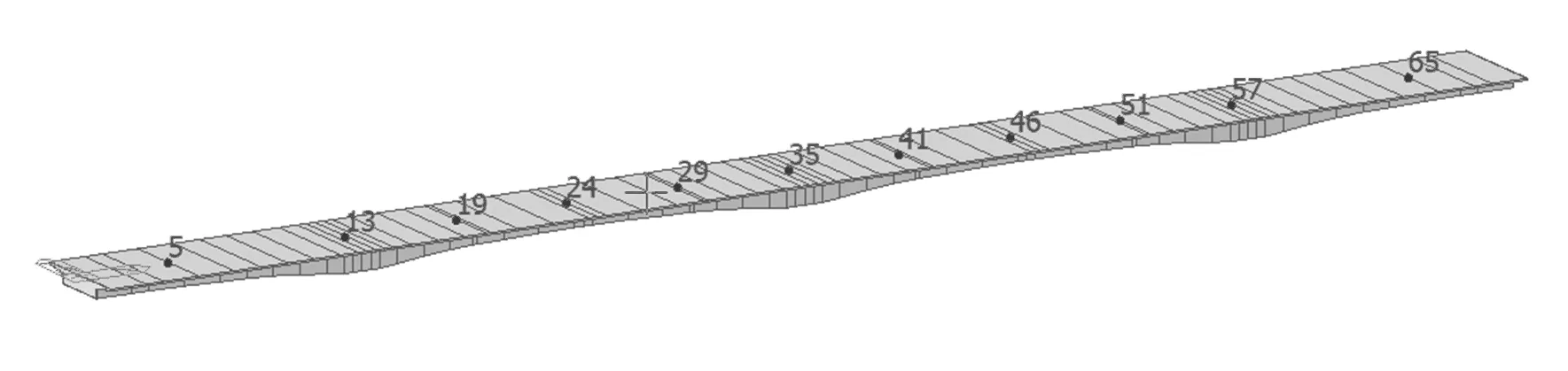
图1 桥梁结构有限元模型

2.2 随机变量统计参数

处于运营期的PC连续梁桥的性能会在众多因素的影响下发生一定的变化,在阅读及参考相关文献的研究基础上[2],选用对连续梁桥可靠度相关系数较大的几个变量作为本文的研究目标(表1)。

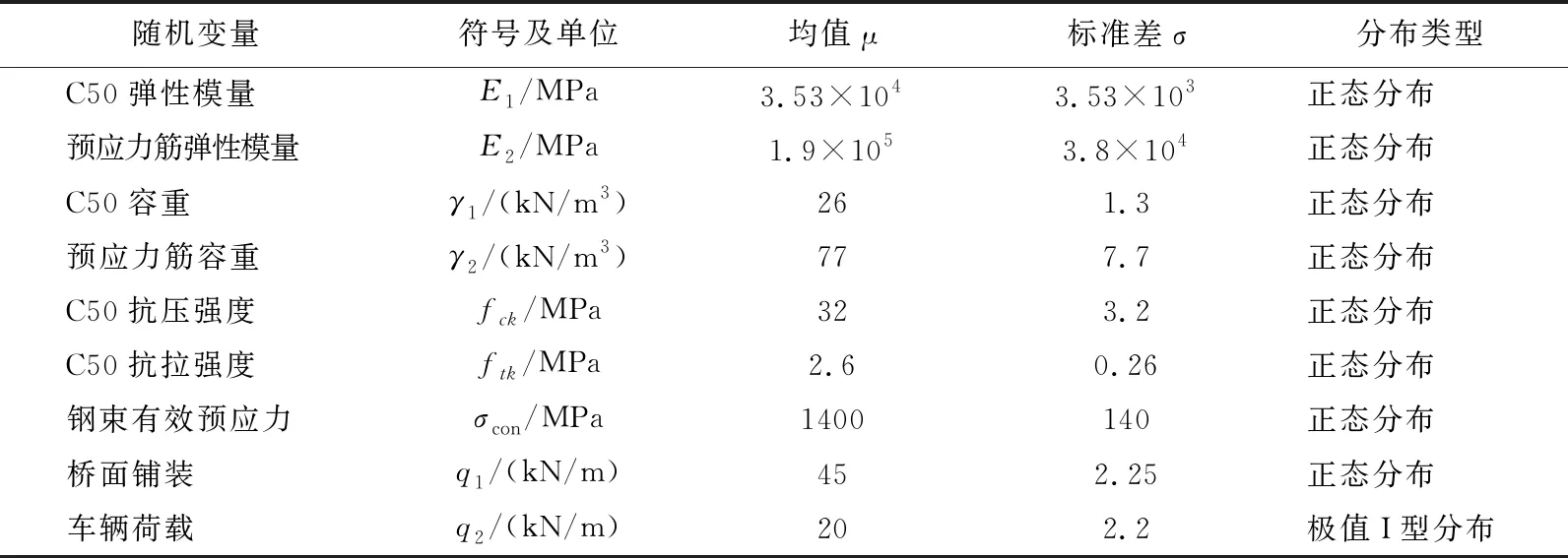
表1 随机变量统计参数表

2.3 失效模式分析

对于构造相对复杂的PC连续梁桥而言,全面地寻找到所有可能的失效模式并计算相应的可靠指标是极其困难的。因此,在查阅相关文献[3,4]并结合该桥实际情况后,本文将桥梁在正常使用极限状态下基于应力限值控制和挠度限制控制的可靠度作为研究的重点,即极限状态函数可表示为:

(11)

式中：σc c为桥梁运营阶段可能失效截面混凝土压应力值;σc t表示相应阶段的拉应力值；桥梁采用的混凝土等级为C50,轴心抗压强度标准值为fc k=32.4 MPa,抗拉强度标准值ft k=2.64 MPa;δ表示桥梁运营阶段可能失效截面挠度值；L表示桥梁的计算跨径。

根据桥梁监控原则、相应荷载试验数据以及参考相关文献[1],选取有限元模型中应力和挠度接近相应失效限值的截面作为可能失效的关键截面。

(1)有限元模型13、35和57号节点对应1#、2#、3#块根部截面将可能出现上缘拉应力失效。

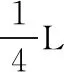
(3)有限元模型24、46号节点对应第二跨和第三跨跨中截面将可能出现下缘拉应力和挠度失效。

各个失效模式下GPR模型评价指标平方相关系数(r2)、平方绝对百分比误差(MAPE)和均方误差根(RMSE)见表2,各个失效模式对应的可靠度指标和失效概率见表3。

表2 各失效模式下GPR模型评价指标

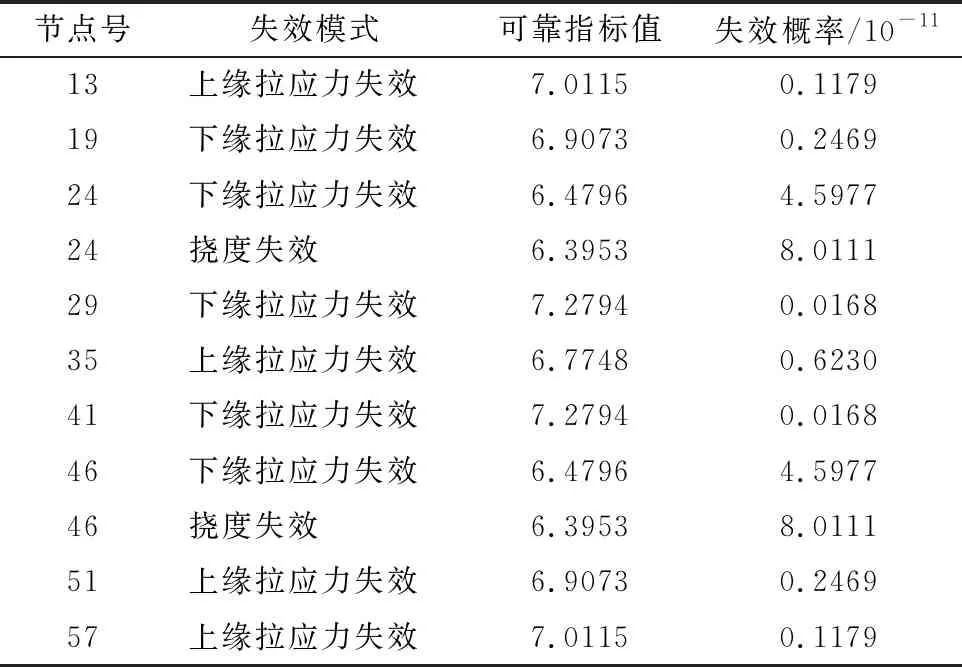
表3 关键截面各失效模式的可靠度指标值

各个失效模式下的GPR模型测试样本的r2值均接近1,说明随机变量和功能函数之间存在很强的相关性。结合相关文献数据,分析测试样本MAPE和RMSE可以知道6个GPR模型预测精度均较高,足以满足工程精度要求。

2.4 计算结果分析

对于正常使用阶段的PC连续梁桥来说,表3中任意一种失效模式的发生都将导致桥梁体系失效,因此本文将仅材料强度失效和挠度失效的桥梁体系视为各个失效模式构成的串联系统。由于该桥梁结构对称,对称截面处功能函数值和可靠指标值对应相等。因此在采用可靠指标矢量法求解体系可靠度时,桥梁结构将被看作是第一跨和第二跨中关键截面的各个失效模式构成的串联系统。可靠指标矢量法失效概率公式为:

(12)

结合表3和式(12)可得,该桥在运营期体系可靠指标为6.313 8,失效概率为1.36×10-10,长湖特大桥的安全等级为一级,查阅相关文献和规范可知,正常使用极限状态下的公路桥梁可靠指标应大于4.7,因此该桥设计符合规范可靠性要求。

3 结束语

本文中将基于统计学习的GPR模型、JC法和可靠指标矢量法相结合,提出了基于高斯过程回归理论的桥梁体系可靠度计算方法。该方法既利用了JC法将非正态分布的随机变量转化成对应正态分布,又充分利用了GPR模型在处理高维度、小样本、非线性回归问题上的优势。通过PC连续梁桥应用实例可以知道,本文采用的方法具有很强的理论基础和实用性,并为解决桥梁结构具有高度非线性隐式极限状态函数的问题提供了一条新的途径。

不过，本文中仅限于对材料强度失效模式和挠度失效模式两种连续梁桥最可能发生的失效模式进行体系可靠度问题的探究,关于该桥型的其他失效模式还有待进一步研究。