钢筋混凝土牛腿受力性能与计算方法研究综述

吴 稳 （同济大学，上海 200092）

1 引言

为了支撑梁等其它上部结构而伸出的短悬臂构件，被称作牛腿。由于构造简单，制作方便，牛腿在建筑、水利、桥梁等工程中应用广泛。

牛腿承受的荷载较大，且多为动载，是结构的关键节点。牛腿与柱交接位置截面高度显著变化，呈现为典型凹角形状，受力状态与连续结构有较大差异；同时，牛腿剪跨比小，剪切变形在牛腿总变形中不可忽略，集中荷载和边界条件对牛腿应力场有显著影响。因此，不能采用传统梁理论分析牛腿力学性能。《混凝土结构设计规范》（GB50010-2010）[1]规定了牛腿构造要求，将使用阶段不出现斜裂缝作为牛腿尺寸限制条件，基于三角桁架模型提出牛腿配筋计算方法，但是该方法偏于保守，与国外《ACI318-11》[2]等规范相比，存在一定差异。本文总结了国内外牛腿试验成果，结合现有研究理论，探讨牛腿计算方法的适用性。

2 牛腿破坏形态和力学性能研究

根据剪跨比（λ）大小，可将牛腿分为λ＞1的长牛腿和λ≤1的短牛腿[3]。长牛腿受力与悬臂梁接近，可按悬臂梁计算理论分析；短牛腿（以下简称牛腿）是工程中更为常见的构造形式。牛腿与悬臂梁受力存在一定差异，主要体现在以下两个方面。①对于悬臂梁，从固定端至加载点，顶缘纵向钢筋应力和底缘混凝土压应力逐渐减小。牛腿试验则表明：从固定端至加载点，牛腿纵向钢筋应力基本保持不变，与桁架中的拉杆类似；加载点与固定端下缘形成斜向受压区，分布比较均匀，与桁架中的压杆类似。②牛腿顶缘1/3高度区域内，纵向钢筋均能在极限状态下发生较大形变而作为受力钢筋。因此，荷载和支承条件对牛腿应力场和受力性能有显著影响，不能将牛腿等效为悬臂梁，而应充分考虑牛腿的局部效应。

2.1 破坏形态

二十世纪七十年代，原冶金部建筑研究院牛腿试验组[3-6]开展了大量有关钢筋混凝土牛腿的试验和研究。对于仅承受竖向荷载的混凝土牛腿，根据剪跨比大小，破坏形态分为以下3类：①λ＞0.75时，斜裂缝随着荷载增加，逐渐向受压区延伸，但几乎不出现分支，直至发生压弯破坏，破坏时刻，钢筋屈服，受压区混凝土压碎；②0.1≤λ≤0.75时，在第一条斜裂缝出现后，随着荷载逐步增加，牛腿内产生大量短小的斜裂缝，并逐渐贯通，导致混凝土剥落，发生斜压破坏。部分牛腿试件在斜裂缝出现后，不产生短小斜裂缝，而是随着荷载增大，斜裂缝出现分支，试件因此破坏，破坏时刻，斜裂缝间混凝土达到棱柱体抗压强度；③λ＜0.1时，加载点与柱交接面上产生多条短斜裂缝，最终牛腿沿该交接面剪切破坏。

图1 牛腿基本破坏形态

王有为等[7]研究了水平荷载对牛腿破坏形态的影响。研究指出，混凝土徐变收缩及温度作用引起的水平荷载较小，不会导致牛腿破坏形态的改变；但是，当地震作用引起的水平荷载大于竖向荷载时，牛腿可能发生斜拉破坏。

2.2 牛腿力学性能研究

丁彦斌[3-6]研究了配筋方式对牛腿力学性能的影响，结果表明：纵向钢筋及斜向钢筋对牛腿斜裂缝的出现基本无影响；增加纵向钢筋和斜向钢筋用量可以在一定程度上限制斜裂缝开展，提高牛腿承载力，随着牛腿剪跨比减小，斜向钢筋对牛腿承载力影响逐渐降低。

为研究牛腿抗震性能，王有为[7]制作了28个牛腿试件，指出反复水平荷载将导致牛腿强度、刚度和变形能力下降。苏三庆[8]建议在纵向钢筋下布置水平箍筋，防止牛腿出现斜拉破坏，增加牛腿承载力和延性，从而改善改善牛腿抗震性能。2002年，袁保禄[9、10]通过 50多个牛腿试验数据，得到牛腿滞回曲线。研究表明，随着纵向钢筋配筋率减小，牛腿刚度和强度略微降低，但滞回曲线稳定，滞回环所包围的面积逐渐增大，耗能增大。合适的配筋率对牛腿抗震性能有重要意义。

鉴于实际工程中牛腿剪跨比较小，李建华[11]基于9个小剪跨比（λ≤0.3）牛腿试验数据，指出牛腿的抗剪强度对小剪跨比牛腿承载能力起控制作用。牛腿的抗剪强度由钢筋的销栓作用、裂缝界面混凝土的咬合作用、裂缝下端剪压区混凝土传递的剪力等三部分组成。随着纵向钢筋配筋率增大，钢筋销栓作用显著，牛腿有一定程度提高。

为了进一步研究钢筋配筋率和斜向钢筋对小剪跨比牛腿（λ≤0.3）受力性能的影响，张思洲等[12]制作了56个钢筋混凝土牛腿试件。试验结果表明，小剪跨比牛腿的裂缝几乎为正裂缝，小剪跨比牛腿破坏时纵向钢筋屈服，斜向钢筋应变仅为纵向钢筋应变的45%～51%，不能充分发挥作用。为充分利用钢筋强度，防止牛腿发生脆性破坏，该研究限制了最大最小配筋率。陈礼和等[13、14]对22个小剪跨比钢筋混凝土牛腿进行了试验研究，结果表明牛腿承载力随混凝土强度等级线性增大；相同荷载下，随着剪跨比增大，纵向钢筋的应变增大；牛腿承载力与剪跨比负相关。

3 牛腿承载力计算方法

将混凝土和钢筋等效为桁架的压杆和拉杆的桁架理论，是早期混凝土牛腿力学模型。随着计算理论的发展，剪摩擦理论[15]、拉压杆模型[16、17]、内力求解法[18]、塑性理论[19]等被用于牛腿力学性能和承载力分析。剪摩擦理论可以较好解释剪力传递机理，拉压杆模型与牛腿试验现象吻合，应用最为广泛。

3.1 桁架理论

1965年，Kriz,L.B.[20]建立了牛腿内钢筋和混凝土压杆组成的三角桁架力学模型，初步确定了混凝土牛腿承载力分析方法。原冶金部建筑研究院基于试验结果，提出实用计算方法，成为《混凝土结构设计规范》牛腿设计依据。

《混凝土结构设计规范》指出，竖向荷载和水平荷载在牛腿顶缘的拉力完全由纵向钢筋承担，为了充分发挥混凝土力学性能，纵向钢筋面积不宜过小，可按式（1）计算：

牛腿是结构重要传力构件，往往需要承担动力荷载。原冶金部建筑研究院指出牛腿使用阶段不宜出现斜裂缝，提出牛腿截面尺寸控制条件，此时，不需要验算混凝土压应力。经过系数调整并考虑水平荷载的影响，《混凝土结构设计规范》采用式（2）限制牛腿截面尺寸：

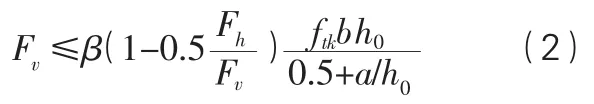
式中，Fv、Fh分别为牛腿上作用的竖向荷载、水平荷载；ftk为纵向钢筋面积；β为钢筋抗拉设计强度；h0为混凝土轴心抗拉强度标准值；β为牛腿裂缝控制系数，吊车梁牛腿取0.65，其他形式牛腿取0.8；h0为截面有效高度；a为竖向荷载与下柱边缘的水平距离，不应小于0.3h0。

3.2 剪摩擦理论

剪摩擦理论[2、15]认为，随着荷载增加，牛腿产生沿下柱端面的竖向主裂缝。极限状态下，穿过裂缝的钢筋屈服，并提供夹合力，即裂缝间正应力，假定剪力通过裂缝间骨料咬合作用产生的摩擦力传递，忽略钢筋消栓作用对抗剪承载力的贡献，裂缝极限摩擦力即为牛腿极限承载力，如式（3）所示。

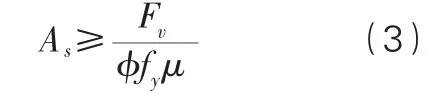
牛腿截面尺寸由抗剪承载力上限值控制，如式（4）所示。

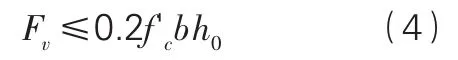
式中，φ为钢筋强度折减系数，可取为0.75；μ为裂缝界面摩擦系数，取为1.4；f'c为混凝土圆柱体抗压强度。

为防止牛腿弯曲破坏，采用剪摩擦理论确定牛腿极限承载力时，需补充计算牛腿根部抗弯承载力，弯矩M按式（5）计算。

3.3 拉压杆模型

《ACI318-11规范》等规范建议通过建立拉压杆模型确定牛腿极限承载力。拉压杆模型是一种塑性力学下限分析方法，由承受拉应力的普通钢筋及预应力钢筋组成的拉杆、承受压应力的混凝土压杆及连接拉杆和压杆的节点组成。根据式（6）-（8）分别计算拉杆 PT、压杆Pc和节点Pn强度，即可得到拉压杆模型的承载力估计。

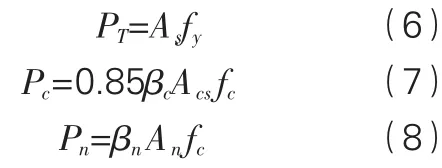
式中，fc为混凝土轴心抗压强度设计值；βc是与混凝土强度有关的系数，对C25～C50取 1.30，C55～C80取 1.35；βn为节点界面混凝土强度软化系数，仅连接压杆的节点取0.85βc，同时连接拉杆和压杆的节点取0.75βc，仅连接拉杆的节点取 0.65βc；Acs、An分别为混凝土压杆和节点界面的截面面积。

对同一牛腿，可建立多种的拉压杆模型，如图2所示。实际结构在极限状态下能否产生足够塑性变形，使荷载按选用的拉压杆模型传递，将直接决定拉压杆模型计算方法的准确性和安全度。Russo G.[19]建立的拉压杆模型计算方便，符合牛腿试验结果。

3.4 计算方法比较

本节选取Yong and Balaguru[21]和Foster[22]部分牛腿试件试验结果，对比《混凝土结构设计规范》采用的桁架理论（方法 1）、剪摩擦理论（方法 2）、Russo G.建议的拉压杆模型（方法3）的适用性，见下表。

方法1裂缝控制条件较严苛，安全系数较大，但也导致了较大的变异系数。方法3安全系数较小，变异系数最小。因此，拉压杆模型最能反映牛腿力学特点和破坏形态。

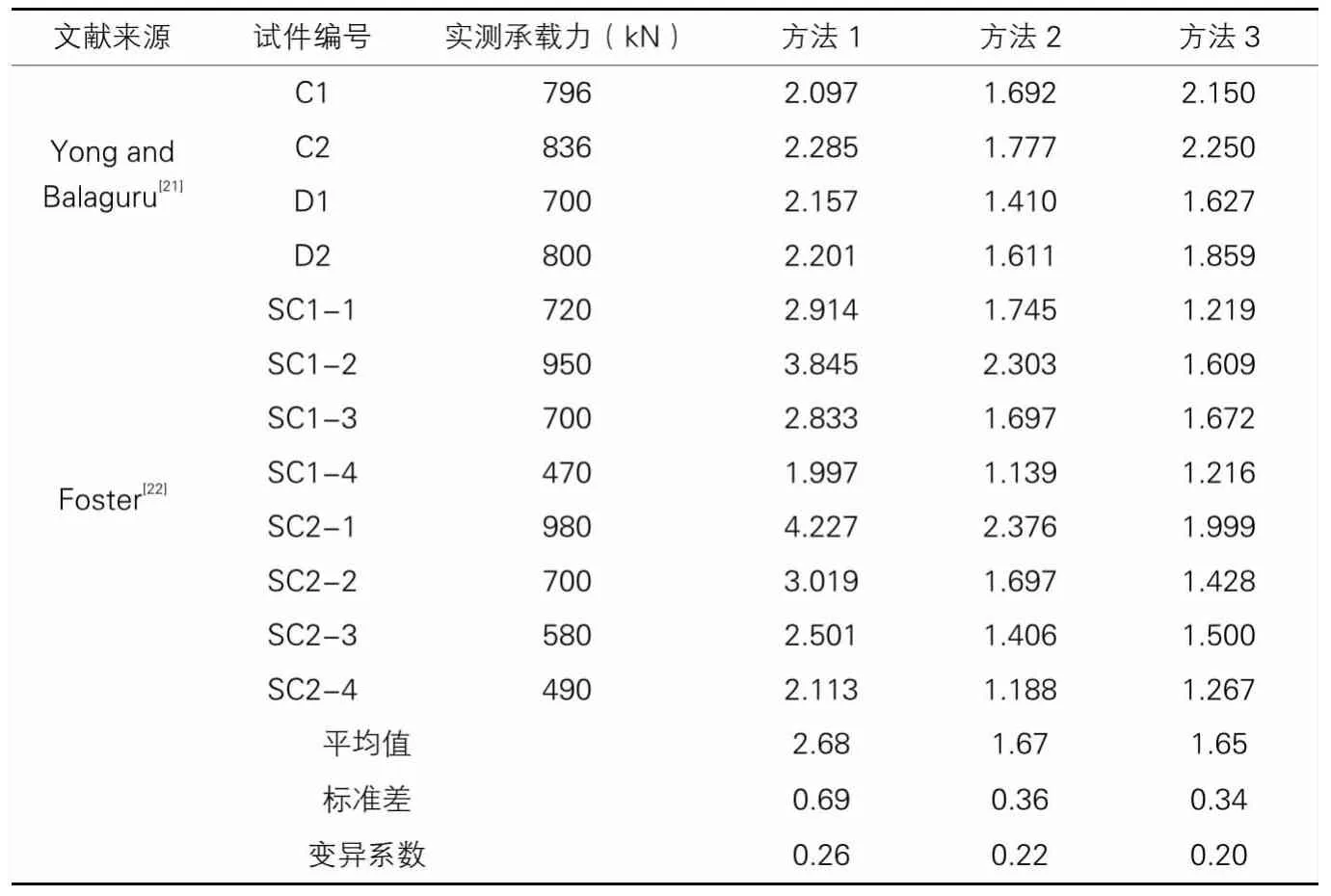
牛腿承载力实测值与计算值比值

4 总结

本文总结了国内外牛腿研究成果，牛腿力学性能与剪跨比、纵向钢筋、混凝土强度、牛腿高度等多种因素有关。通过牛腿试验结果对比国内外主要牛腿承载力计算方法的适用性。结果表明，《混凝土结构设计规范》建议的计算方法具有较高的安全系数，拉压杆模型则与试验结果最接近。