基于EEMD-JADE的桥梁挠度监测中温度效应的分离

谭冬梅，刘晓飞，姚欢，聂顺，吴浩

(1.武汉理工大学 道路桥梁与结构工程湖北省重点实验室，武汉 430070；2. 武汉地铁运营有限公司，武汉 430017； 3.华中师范大学 城市与环境科学学院，武汉 430079)

挠度是桥梁结构损伤诊断和安全评估的关键参数之一，能够直观、有效地反映桥梁结构的整体综合性能。运营期通过传感器监测得到的桥梁结构挠度是车辆荷载、温度荷载以及混凝土的收缩徐变等因素共同作用下的综合响应。将温度效应分离出来后，能清楚地得到仅由车辆动荷载作用得到的高频振动信号，剔除掉环境、温度的影响后，能更加方便地达到损伤识别等目的。因此，准确分离出桥梁在各个因素作用下的挠度特性有助于正确诊断桥梁结构病害，为桥梁的工作性能与安全评估提供可靠的依据。

目前，已有学者对桥梁挠度分离进行研究。分离的方法主要分为有限元法以及信号处理。从建立精确的模型出发，袁俊桃等[1]采用“时间-温度-变形”同步测量的方法，将实测结果与MIDAS仿真结果进行对比分析，证明箱梁温度场对桥梁挠度影响较大。赵晓健等[2]以顺德支流特大桥为背景，基于温度实测值对本桥进行温度效应仿真分析，主要分析了温度变化对桥梁挠度和应力的影响，并且将温度变化引起的挠度值与实测值进行对比。然而，在实际工程中，桥梁所处的环境因素较为复杂，且各环境因素之间存在相互耦合作用的现象，因此，通过数值仿真分析来准确计算实际桥梁工程挠度中的各挠度组分并不能得到准确的结果。随着信号处理技术的发展，学者们开始从信号处理的角度进行桥梁各挠度组分的分离研究。梁宗保[3]以小波多尺度分析为手段提取活荷载挠度信号，对大量温度与挠度数据进行统计分析，精确地模拟出二者之间的函数关系并得到回归方程，在已知实测温度的情况下，利用回归方程计算并剔除温度效应。刘纲等[4]利用各挠度组分之间在时间尺度上不耦合的特点，结合粒子群优化算法和滤波算法自适应改变日温差效应时间尺度的频率带宽，通过回归统计分析分离出监测信号中的温度效应。粒子群优化算法对于频率接近的信号分离效果通常较差，计算过程中的收敛速度较慢。刘夏平等[5]提出基于最小二乘支持向量机来进行挠度温度效应分离的方法，将温度看作变量，温度效应视为函数，应用最小二乘支持向量机的逼近能力，建立温度和温度效应的函数关系。杨红等[6]在刘夏平研究的模型基础上，提出一种基于多最小二乘支持向量机建模方法，该模型在拟合逼近温度与挠度的映射关系上更为精确，因此，通过多最小二乘支持向量机模型分离所得到的结果也更为准确。但随着所采集数据量的增大，该算法计算所需时间也越长，并且其计算过程也比较复杂，不能完全保证训练过程的收敛性，在实际工程中运用较少。Tang等[7]、杨红等[8]、唐春会[9]通过传统的经验模态分解对信号进行升维，然后进行独立分量分析。该方法在经验模态分解过程中容易出现模态混叠的问题，使分离结果产生较大误差。同时，分解过程中不可避免地会出现虚假的IMF分量，在实际应用中区别特征信号与虚假IMF分量存在一定难度。

针对上述方法存在的弊端，笔者提出一种基于EEMD-JADE的分离算法。首先，利用EEMD将单通道的混合挠度信号进行分解；然后，采用基于能量熵增量的判别法识别并剔除虚假的IMF分量；最后，采用JADE对所得信号进行分离。相比于传统的EMD，EEMD在其分解步骤上进行了改进，能够较好地抑制模态混叠,而虚假的IMF分量也能迅速地被基于能量熵增量的判别法识别。

1 理论框架

1.1 EEMD算法

经验模态分解(Empirical Mode Decomposition，EMD)的主要思想是把一个时间序列的信号分解为频率由高到低的不同尺度的IMF分量[10]。模态混叠是其主要的缺点，信号时频分布会因模态混叠产生严重偏移，同一个IMF分量上会出现不同的物理成分，同时，后续的IMF蕴含的物理意义也会遭到破坏，以致严重影响分解效果[11]。

针对模态混叠问题，Huang等[12]在传统的EMD方法上进行了改进，提出了一种基于白噪声的集合经验模态分解法(Ensemble Empirical Mode Decomposition，EEMD)。模态混叠本质上是由于信号的IMF不连续造成的。白噪声的计入可以为分析信号提供一个相对一致的参照尺度分布，保证每个IMF分量时域的连续性以抑制模态混叠。EEMD算法具有良好的适应性和较高的时频分辨率，非常适合非线性、非平稳信号的分析[13]。

1.2 基于能量熵增量的EEMD虚假IMF分量识别

1.2.1 信息量的定义 信息量是信息多少的量度，其大小可以用熵来衡量，美国数学家Shannon以概率论为基础得出了信息量的计算公式

I=-plog2(p)

(1)

式中：I为信息量；p为事件发生的概率。

1.2.2 IMF能量熵增量函数 在EEMD分解得到的IMF分量中，每个IMF分量包含不同的频率成分，具有不同的能量，由于插值误差、端点效应等原因，在EEMD分解过程中，常常会产生虚假IMF分量。有效的IMF分量所占能量较大，而虚假IMF分量所占能量较小[14]。为了刻画出这种能量之间的差别，将信息量的概念引入IMF能量分析中。通过构建能量熵增量函数来表示各个IMF分量在整个系统中所占能量的大小。该算法的过程如下：

1)计算每个IMF分量的能量

(2)

2)对所有IMF分量的能量进行归一化处理

(3)

式中：M为IMF分量的个数。

3)IMF分量能量熵增量的计算

ΔQi=-p(i)log2(p(i))

(4)

有效IMF分量的能量熵增量较大，而虚假IMF分量的能量熵增量小，二者一般存在数量级的差别。对于能量熵增量较小的虚假IMF分量，予以剔除。

1.3 JADE分离算法

JADE算法是由Cardoso等[15]提出的一种建立在“四阶累积量矩阵对角化”概念基础上的独立分解改进算法。该方法主要是利用独立信号间互累积量为零的特点[16]，引入多变量数据的四阶累积量矩阵，通过对这些矩阵进行联合对角化来求解分离矩阵，既简化了算法，又提高了结果的稳健性。相比于传统独立成分分析，JADE算法对高斯噪声不敏感，可以反映高阶相关的非线性关系[17]。

JADE算法流程如下：

1)观测信号的球化处理

假定观测信号X(t)是由N个相互独立的源信S(t)=[S1(t),S2(t),…,SM(t)]T与一个M×N的混合矩阵A相乘得到，即

X(t)=AX(t)=[X1(t),X2(t),…,XM(t)]T

(5)

对于球化矩阵W，由观测信号的自相关矩阵特征值分解求得[18]，因此，球化后的信号为

z(t)=WX(t)=WAS(t)=US(t)

(6)

式中：U为酉矩阵。

2)四阶累积量的计算

z(t)的四阶累积量矩阵

(7)

式中：1≤i,j≤N,mkl是矩阵M的第k行，l列所对应的元素。

3)酉矩阵U的确定

累积量矩阵集合

(9)

在计算过程中，通过使式(9)所示函数的最大化来实现累积量矩阵集合的联合近似对角化，从而确定酉矩阵U。

4)源信号的估计

确定酉矩阵U后,混合矩阵的估计值

(10)

最终源信号的估计值

(11)

1.4 EEMD-JADE算法

受端点效应的影响，EEMD在对频率接近的低频信号进行分离时，往往无法得到精确的结果。而盲源分离能够较好地实现频率接近的低频信号的分离，但在进行盲源分离时有一个重要的前提条件，即观测信号数必须大于振源数，当这个条件无法满足时，就会造成分离的失败。先通过EEMD将挠度信号转换成为一系列IMF，将单通道信号转换成多通道信号，再将剔除虚假模态分量后的IMF求取能量熵增量，选取能量熵增量较大的IMF作为JADE算法的输入信号，这样就做到EEMD与JADE算法相结合，JADE改进了EEMD模态混叠和端点效应的弊端，而EEMD又达到了JADE所要求的观测信号大于源信号数目的先决条件。从而利用两种算法优势互补来分离桥梁挠度信号中的低频成分。

2 桥梁仿真挠度信号分离

2.1 挠度模拟信号

以图1所示的某斜拉桥为背景桥梁模型，截面形式、材料参数等见表1。建立模型所用材料参数：主梁弹性模量为2.059 4×108kN/m2，泊松比0.3，采用梁单元，索塔混凝土弹性模量为3.432 3×107kN/m2，泊松比为0.17，采用梁单元；斜拉索弹性模量为1.912 3×108kN/m2，泊松比为0.3，采用索单元。线膨胀系数为1.21×10-5℃-1。边界条件：6个辅助墩以及2个桥塔与地面均采用固支；6个辅助墩与梁之间均采用两节点刚性连接，桥塔结合处也采用刚性连接；梁与梁之间均采用弹性连接。应用Midas对其进行结构变形仿真分析，获取其变形值。

图1 斜拉桥的模型图Fig.1 Model diagram of cable stayed bridge

弹性模量/MPa截面积/m2一期恒载换算密度/(kg·m-3)二期恒载换算密度/(kg·m-3)2.1×1051.9113.04×1033.14×103

注：截面积为标准钢箱梁断面；一期恒载换算密度不包括桥墩处压重的质量。

假设截面温差沿截面高度线性变化。整体每升温1 ℃，主跨跨中下挠1.44 mm；截面线性升高温差1 ℃，主跨跨中下挠0.23 mm。假设日温差和年温差均为按正弦变化的周期性函数，取每天的整体日温差12 ℃，截面日温差6 ℃以及年温差35 ℃。由此可得整体日温差T11=6×sin(πt/12)，截面日温差T12=3×sin(πt/12)，年温差T2=17.5×sin(πt/4 380)。

假定温度与桥梁结构变形呈线性关系，则整体日温差效应f11=-8.64×sin(πt/12)，截面日温差效应f12=-0.69×sin(πt/12)，日温差效应f1=f11+f12，年温差效应f2=-25.2×sin(πt/4 380)。

假设长期挠度由预应力损失、混凝土收缩徐变以及结构损伤等因素引起，采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD 62—2004)计算该桥梁长期挠度变形f3，并用指数型函数进行拟合，得到长期挠度变形[4]。

根据挠度加法模型，跨中总挠度由日温差效应、年温差效应及长期挠度构成[19]，即f=f1+f2+f3，式中挠度的单位为mm;t为时间，单位为h，各挠度信号的时域曲线与频谱图如图2所示。

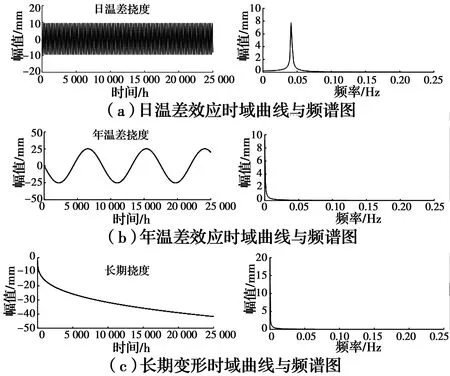
图2 各挠度效应的时域和频谱Fig.2 Time domain and frequency spectrum of the deflection

2.2 模拟挠度信号的分离

跨中总挠度时程曲线如图3所示。

图3 总挠度的时程曲线Fig.3 Time history curve of the total deflection

对跨中总挠度信号进行EEMD分解，得到13个IMF分量与一个趋势项。仿真信号中只包含3个频率成分，由此可见，在分解的过程中产生了较多的虚假IMF分量。各阶IMF分量的能量熵增量函数曲线如图4所示。由图4可知，IMF4、IMF11以及IMF14对应的能量熵增量较大，可作为IMF主分量；其余阶次所对应的能量熵增量几乎为0，可以认为是虚假的IMF分量，予以剔除。

图5是时域相关系数与能量熵增量函数的比较图，运用时域相关系数所识别得到的主分量是IMF3、IMF4、IMF10、IMF11、IMF12、IMF13和IMF14。并且其中几项IMF分量的相关系数之间的差别较小，难以进一步区分虚假的IMF分量，故利用基于能量熵增量函数识别虚假IMF分量成分相比传统时域相关系数识别度更高。选取第4阶、11阶以及14阶IMF分量组成多通道的混合信号，其中，IMF4、IMF11、IMF14信号图以及各自的频谱图分别如图6、图7所示。从频谱图中可以清楚的看出IMF4对应了日温差效应；IMF11对应年温差效应；IMF14趋势向对应长期挠度。再利用JADE盲源分离算法估计出源信号。

图4 仿真信号能量熵增量曲线Fig.4 Energy entropy increment curve of simulation signal

图5 时域相关系数与能量熵增量函数的比较Fig.5 Comparison of time-domain correlation coefficient and energy entropy increment function

图6 EEMD分解后IMF主分量Fig.6 IMF principal component after EEMD decomposition

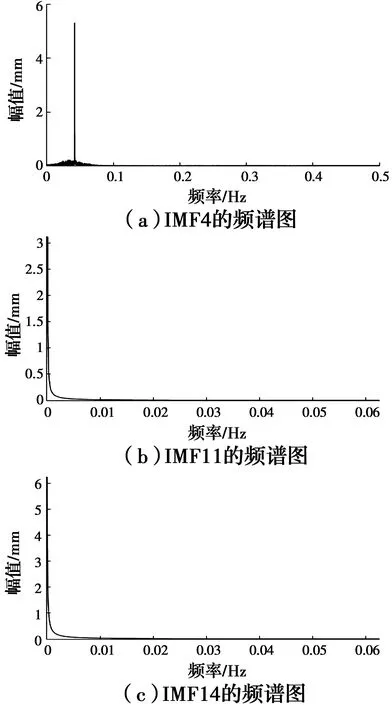
图7 主分量频谱图Fig.7 Principal component spectrogram

为克服分离结果幅值的不确定性，对分离结果和原选取的IMF进行傅里叶变换，然后进行幅值对比，将其比值作为系数与分离结果相乘[9]，得到最终的结果，如图8所示。与图2比较可以看出，分离得到日温差效应与年温差效应与对应的原始信号时域曲线基本相同，分离效果较好。分离出的长期挠度在整体上存在一定的波动性，这是由于受到了频率接近的年温差效应的干扰[9]，但是整体上仍然保留着与原始信号相一致的变化趋势。

图8 分离后的挠度时域曲线图 Fig.8 Time domain curve of deflection after separation

2.3 分离效果评价

(12)

式中：cov(•)为协方差运算。|ρi|的值越接近于1，分离效果越好，相关系数与二次残差见表2。

表2 模拟信号分离前后的信号相关系数Table 2 Correlation coefficients of analog signals before and after separation

由表2中相关系数可知，日温差效应与年温差分离较为精确，而长期挠度在分离过程中受到年温差效应的干扰，相关系数小一些。总体上各相关系数均接近于1，说明分离效果较好。

3 实测桥梁挠度信号分离

3.1 实测桥梁挠度信号分离

某桥梁是双塔双索面混合型斜拉桥。主桥为双塔双索面钢箱梁与预应力混凝土箱梁组合型斜拉桥结构，主墩基础为自浮式吊箱围堰高桩承台基础。桥型布置如图9所示。

图9 桥型布置图Fig.9 Layout of the bridge

该桥梁安全监测项目主要针对大桥桥体，采用北斗卫星导航定位技术，在桥梁关键部位设计布设北斗桥梁监测站，监测桥梁日常运行状态。北斗卫星导航定位技术作为一种全新的现代空间定位技术，能实时自动提供连续的观测值，具有全天候、高精度、点间不需相互通视等特点[22]。利用北斗导航定位技术的高精度实时差分定位和事后差后定位[23]，可以随时掌握桥梁的结构变形，为桥梁的运营管理、安全评估以及科学研究提供可靠的依据。项目所采用的北斗监测站如图10所示。

图10 北斗监测站Fig.10 The Beidou monitoring station

提取主跨跨中下游和上游测点的挠度数据，时间段为2017年10月13日02：00到2017年10月15日02:00，采样频率为10 min。各测点的挠度时程曲线如图11所示，从整体上看，主跨跨中竖向挠度的日变化曲线整体呈现三角函数变化特征。温度与主梁的竖向挠度之间存在较强的相关性[24]，并且温度作用的变化决定了挠度的变化趋势[25]。

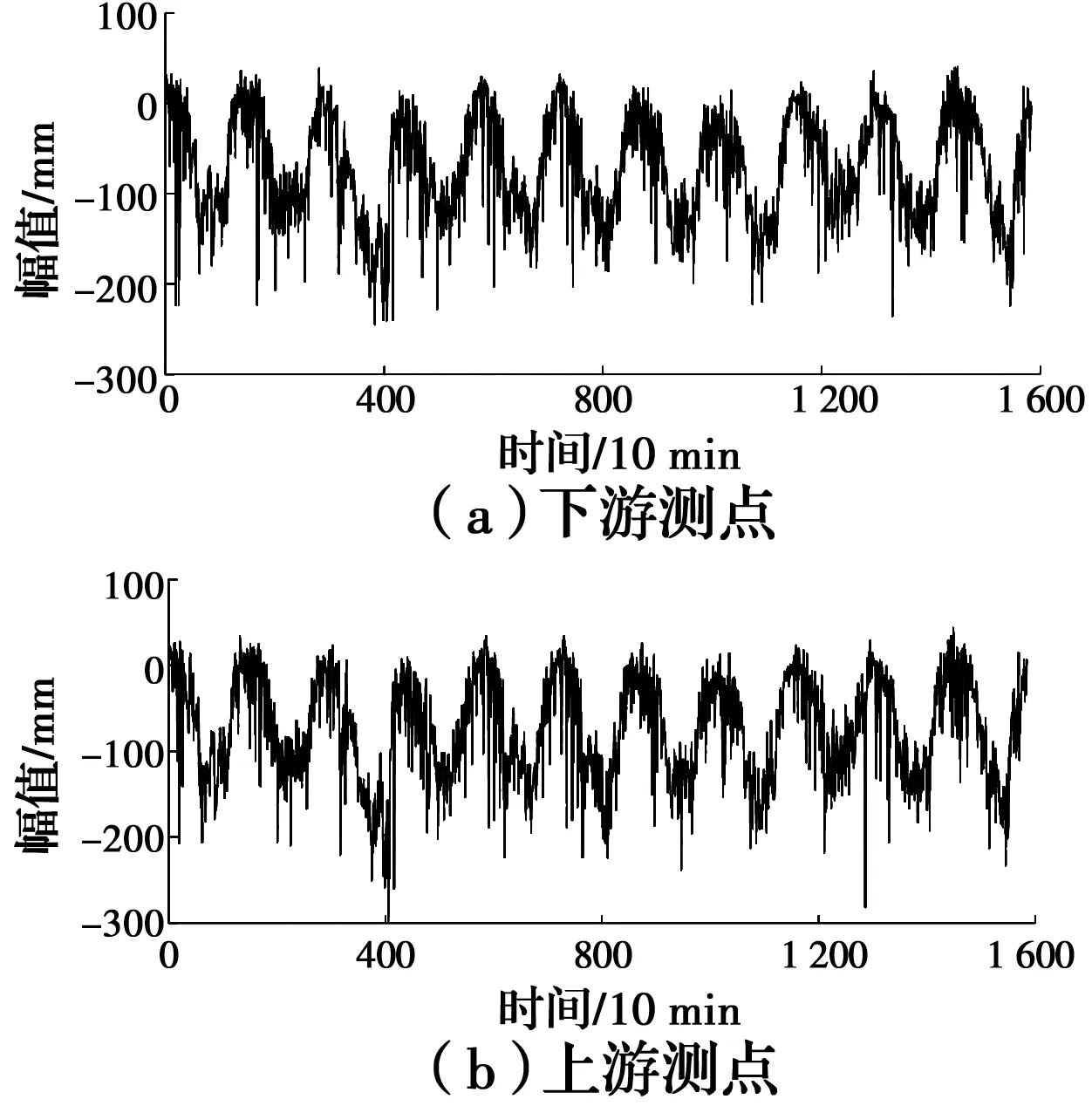
图11 实测挠度时程曲线Fig.11 Actual deflection history

3.2 实测挠度数据的处理

挠度监测信号可以认为主要是由环境噪声与车辆荷载产生的挠度、日温差效应、年温差效应以及长期挠度所组成的。环境噪声与车辆荷载产生的挠度分布在信号的高频部分，与其他信号的频率差别较大，可以借助低通滤波方法剔除高频信号。由于移动平均滤波算法简单，计算效率高[26]，故采用移动平均滤波算法对实测挠度信号进行低通滤波。滤波后的挠度时程曲线如图12所示。

图12 滤波后的挠度时程曲线Fig.12 Actual deflection history after filtering

通过滤波算法剔除车辆荷载效应以及环境噪声等高频信号后，剩余变形可以认为是由日温差效应、年温差效应和长期挠度变形所组成的。由于取样的时间跨度远小于其年温差效应以及长期挠度的周期，采集的信号无法表示出年温差效应以及长期挠度完整的变化规律，故只考虑日温差效应的分离。

3.3 实测信号分离及结果评价

现对滤波后的挠度信号用EEMD-JADE方法进行分离。首先对滤波后的挠度信号进行EEMD分解，得到一系列的IMF分量，然后利用能量熵增量识别虚假的IMF分量。时域相关系数与能量熵增量函数的比较如图13所示。采用相关系数进行识别得到的主分量是IMF4、IMF5、IMF6和IMF7，而其中部分IMF分量之间数值差别较小，难以识别。而采用能量熵增量识别得到的主分量为IMF5与IMF9，且二者与其他阶次的IMF所对应的数值相差较大，故可将IMF5与IMF9作为主分量。

图13 实测信号时域相关系数与能量熵增量函数的比较Fig.13 Comparison of time-domain correlation coefficient and energy entropy increment function of the measured signal

将选取的主分量与滤波后的信号作为JADE盲源分离的模型输入信号，再通过JADE算法分析与处理，最终估计出源信号。由于两测点处于对称位置上，理论上两测点的日温差效应相同。现将两测点处分离出的日温差效应进行对比，其结果如图14所示。由图14可知，两测点处分离出的日温差效应的重合度较高，相关系数达到了0.996 9，与理论分析一致，说明该方法能够较好地分离出日温差效应。

图14 日温差效应对比Fig.14 Comparison of daily temperature difference effect

由于年温差效应的周期远大于日温差效应的周期，采集11 d的挠度信号当中不足以呈现出年温差效应的周期性变化特征。现采集时间跨度为一年的主跨跨中挠度数据，采用基于EEMD-JADE分离法分离出日温差效应与年温差效应。采样频率为每小时一次，采集到的挠度信号如图15所示。

图15 实测一年挠度时程曲线Fig.15 Actual deflection history of one year

首先对实测挠度信号进行滤波处理，滤除掉属于高频成分中的车辆荷载效应和环境噪声，然后采用EEMD-JADE方法分离出日温差效应与年温差效应，具体的分离过程这里不再赘述，最终分离所得到的结果如图16与图17所示。

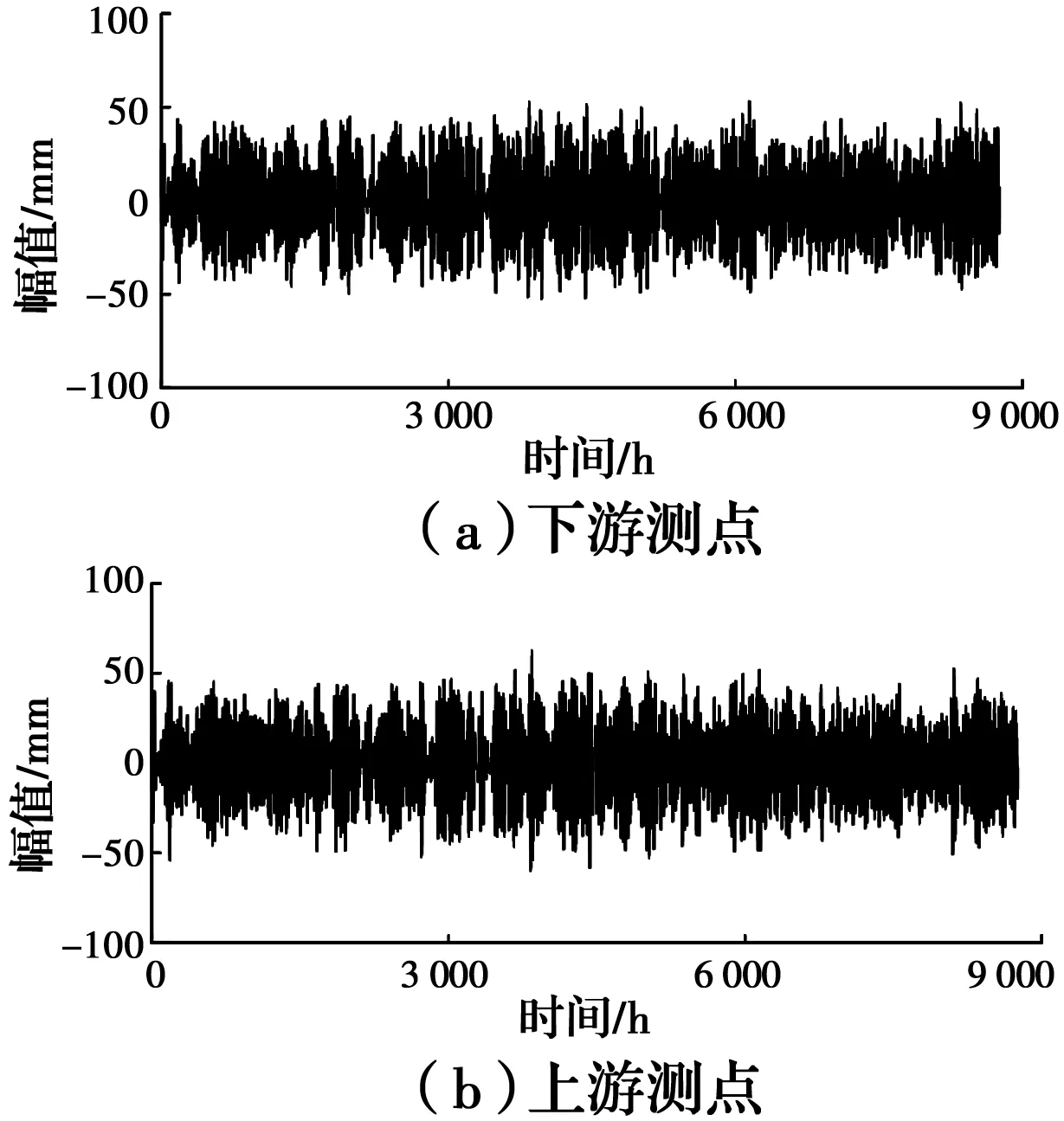
图16 分离后信号日温差效应Fig.16 Daily temperature difference effect after separation

由于年温差时间跨度比较长，年温变化比较简单，而且年温变化主要引起结构轴线方向的长度变化，只有当这种纵向变形受到约束时，才会引起附加的温度应力，并且由于变化缓慢，会受到混凝土徐变等影响而削弱，因此使得年温差效应幅值小于日温差效应。同时，考虑实际长期挠度受多种复杂因素影响，故针对实际信号，只给出日温差效应与年温差效应。

图17 分离后信号年温差效应Fig.17 Yearly temperature difference effect after separation

采用相关系数对分离结果进行评价，其结果见表3。

表3 对称位置分离的温度效应相关系数Table 3 Temperature effect correlation coefficients of symmetric position separation

由表3可知，处于对称位置测点处分离出的日温差效应与年温差效应的相关系数均在0.9以上，说明温度效应得到了较好的分离。

4 结论

1)利用EEMD把单通道混合信号按不同尺度特征分解到不同的子空间中，构建出虚拟多通道，信号由一维转化至高维，解决了单通道信号的欠定问题。同样地，盲源分离算法解决了EEMD分解过程中产生的IMF分量的模态混叠以及端点效应，两种算法可以优势互补。

2)通过能量熵增量法识别并剔除虚假IMF，突出了有用的特征信息，有效地改善了EEMD分解中的模态混叠现象。

3)模拟信号与实测信号的分离结果表明，分离值与实际值的相关系数接近理想值，说明该算法是一种较为精确的算法。

4)建立桥梁挠度信号分离模型时，并没有考虑风荷载、骤降温差的影响，而这些影响因素都客观存在。因此，在以后的研究中可将风荷载以及骤降温差效应纳入到总挠度成分中。传感器会随温度的变化而产生变化，如何从挠度监测数据中分离出这一部分数据，还需要做进一步的研究。