竖向及水平地震作用下PSRC空腹桁架转换结构抗震性能分析

陈勇，简斌，龚春玉

(1. 东莞市大业施工图审查有限公司，广东 东莞 523000；2.重庆大学 山地城镇建设与 新技术教育部重点实验室；土木工程学院，重庆400045)

梁式转换结构形式简单、传力明确，是实际工程应用中最常用的转换结构方案。但随着跨度增大，转换梁截面尺寸也急剧增大，导致建筑空间和使用功能受到极大影响，抗震设计中也将面临“刚度突变”、“强梁弱柱”等突出问题[1-2]。预应力型钢混凝土(简称PSRC)空腹桁架转换层结构，是现代预应力、型钢混凝土组合结构与空腹桁架转换层的优化组合，具有转换跨度大，转换层构件截面尺寸远小于梁式转换的优点，可很好地满足建筑使用功能需求。

空腹桁架转换层结构属于典型的竖向不规则形式，其抗震设计是其结构设计的关键[3-4]。傅传国等[5]、戴国亮等[6]完成了PSRC空腹桁架转换结构拟动力地震反应试验研究，结果表明，该类结构更容易实现多道防线设防的抗震设计。张誉等[7]完成了梁式和空腹桁架式转换层结构竖向荷载和水平低周反复荷载试验研究，结果表明，后者具有更理想的破坏形态及抗震性能。简斌等[8]依据“强化转换层及下层、相对弱化上部结构”的基本原则，完成了一榀1/4缩尺PSRC空腹桁架转换层结构低周反复荷载试验，实现了预设的延性破坏模式。但该类结构研究目前存在一些不足：试验研究难度大，其子结构模型边界条件、地震作用与实际差异大，实验构件转换层为单跨结构等；大多已有研究未明确说明其试验模型设计的具体原则方法，导致设计依据不明确，对工程设计的指导意义降低；缺少精细化的有限元弹塑性时程分析，且对于大跨度结构，模拟分析未考虑竖向地震作用的影响。

笔者针对8度(0.2g)设防地区，在OpenSEES软件平台上建立PSRC空腹桁架转换层结构精细化有限元模型，考虑竖向及水平地震动共同作用，在罕遇、极罕遇水准下完成弹塑性时程分析，对大震下的破坏模式、抗倒塌性能和竖向地震作用的影响进行研究。

1 算例设计

1.1 设计基本原则

依据现行相关规范[2]和研究成果，确定PSRC空腹桁架转换层框架结构设计的基本原则：

1)“强转换”原则。即“对转换层及其下部结构进行强化，而相对弱化转换层的上抬框架”。

2)多道防线抗震设防原则。首道防线为转换层上抬框架梁柱(不包括与桁架上弦梁紧邻的上层柱)，其次为空腹桁架中腹杆、上弦梁和与其紧邻的上层框架柱，而桁架下弦梁和转换柱则作为最后一道防线。

3)上抬框架部分应满足现行规范有关普通RC框架“强柱弱梁”的设计原则。

1.2 算例基本信息

以两跨PSRC空腹桁架转换层平面框架结构为研究对象，算例基本信息见表1，KJ1和KJ3为转换跨度不同的基本算例，研究该类结构的基本抗震性能；算例KJ2、KJ3及KJ4竖向地震作用强度不同，研究竖向地震下的结构反应。

表1 算例基本信息Table 1 Information of examples

注：H/V为竖向与水平向地震作用加速度峰值比。

除表1所列基本信息外，各算例均为9层，底层层高6 m、2层(转换层)层高4.5 m、3～9层层高3.3 m。上抬框架跨度：KJ1为6 m，KJ2～KJ4为8 m。板厚：屋面板厚120 mm，转换桁架上下层楼板厚180 mm，其他楼面板厚100 mm。转换桁架沿纵向布置，横向每隔2 m设置一道次梁。此外，地震分组为第一组、Ⅱ类场地。

1.3 算例设计

算例均为大跨度转换，故在空腹桁架下弦采用PSRC梁，转换柱(1～2层柱)采用型钢混凝土柱，其他构件均为普通钢筋混凝土。

由于下弦PSRC梁为主要转换构件，其截面尺寸相对较大，为避免出现 “肥梁瘦柱”和方便施工，设计时给出转换柱截面宽度不小于下弦梁宽度等限制。经多次试设计后，各算例构件截面尺寸如图1所示，轴压比和层间位移角等均满足相关限值要求。

表2给出了转换层等效剪切刚度比和最大轴压比，计算结果表明，空腹桁架转换层刚度明显大于上下相邻楼层。在实际工程中，此项指标可以通过增设型钢构件、提高型钢含钢量或调整上下弦梁等构件的相对刚度进行改善。之所以仍允许较大刚度变化，是为了研究在规范限值范围内，较大刚度变化可能的不利影响。

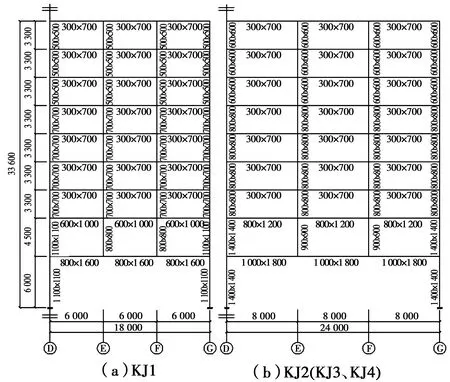
图1 构件截面尺寸Fig.1 Dimension of component section

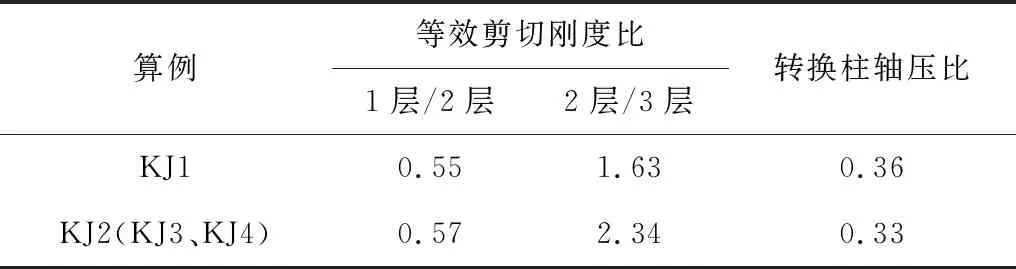
算例等效剪切刚度比1层/2层2层/3层转换柱轴压比KJ10.551.630.36KJ2(KJ3、KJ4)0.572.340.33

算例设计过程中，荷载按现行规范要求取值，竖向地震采用重力荷载代表值的10%，不考虑风荷载作用。根据中国现行规范[2，9]、多道防线抗震设防思想以及前期初步研究结果[10]，对构件的内力标准值进行了调整，相关调整系数见表3。其中，考虑到桁架下弦采用PSRC构件，其配筋多为抗裂、预应力度或型钢配置等构造要求控制，使其实际抗弯承载力远高于抗震计算需求。若按下弦实际配筋调整，将导致与下弦相连的转换柱端配筋量大增而难以实现。因此，在考虑“强柱弱梁”时，对1～2层转换柱上下端及3层框架柱底均按内力组合值进行调整，并根据前期研究结果初步取1.7的弯矩放大系数进行研究。同时，为了使空腹转换桁架上、下弦跨中节点不早于腹杆发生破坏，腹杆仅考虑“强剪弱弯”，不考虑“强柱弱梁”[8]，地震下腹杆可以出铰，但不破坏。

各算例构件纵向钢筋配筋结果如图2所示，其中，桁架下弦PSRC梁参考现行规范[11]进行配筋计算。梁上部纵筋截断位置为1/3处，图中不再标出；柱对称配筋，图中仅显示单侧值；转换桁架下弦PSRC梁和转换柱中型钢为实腹H型钢，含钢率约为5%，居中布置，其截面尺寸见图2。桁架下弦PSRC梁每跨预应力线型采用4段抛物线，材料选用1 860级钢绞线，张拉控制应力为0.75fptk，预应力损失取25%。

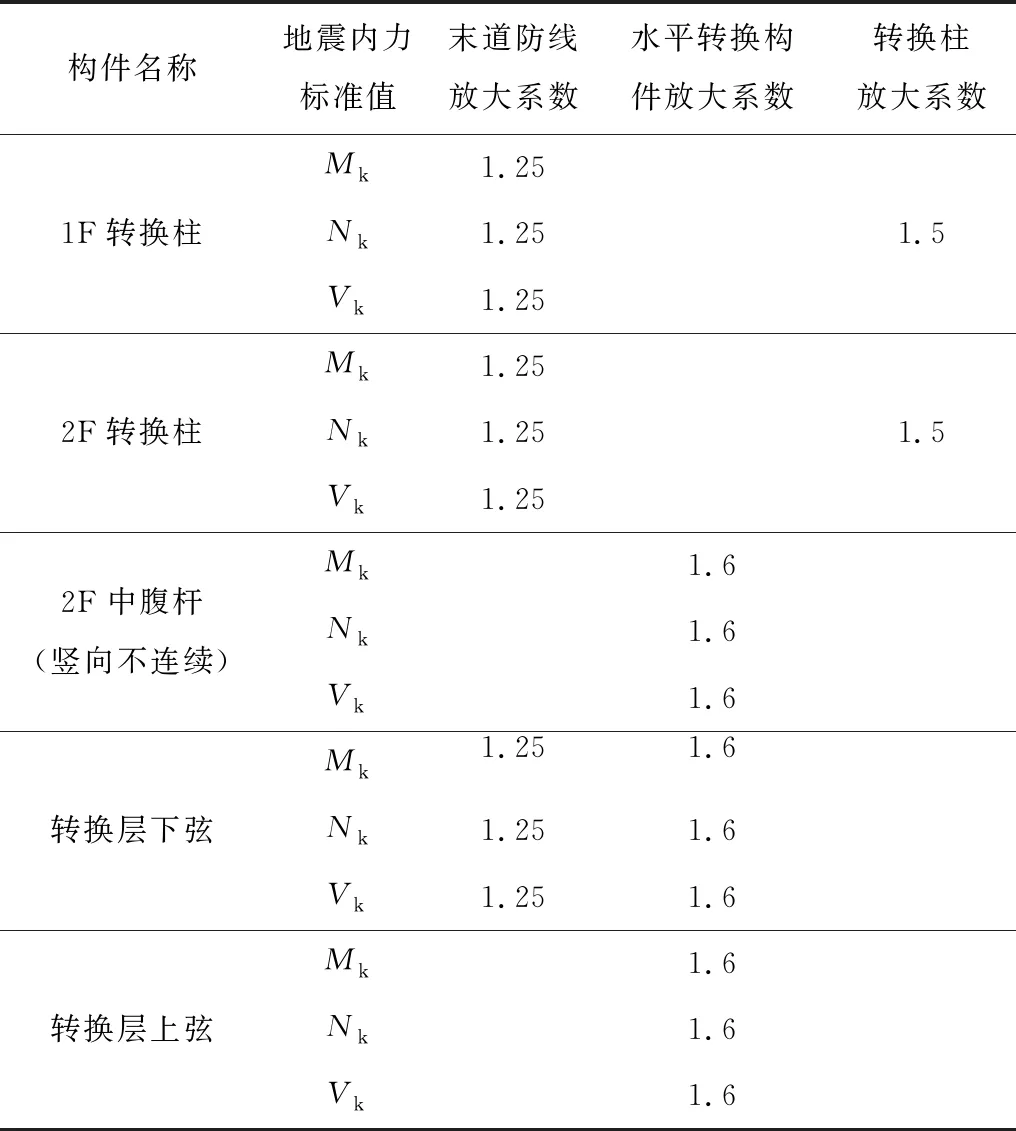
表3 转换层各构件及首层柱内力调整系数Table 3 Regulation factor for the internal force of transfer story

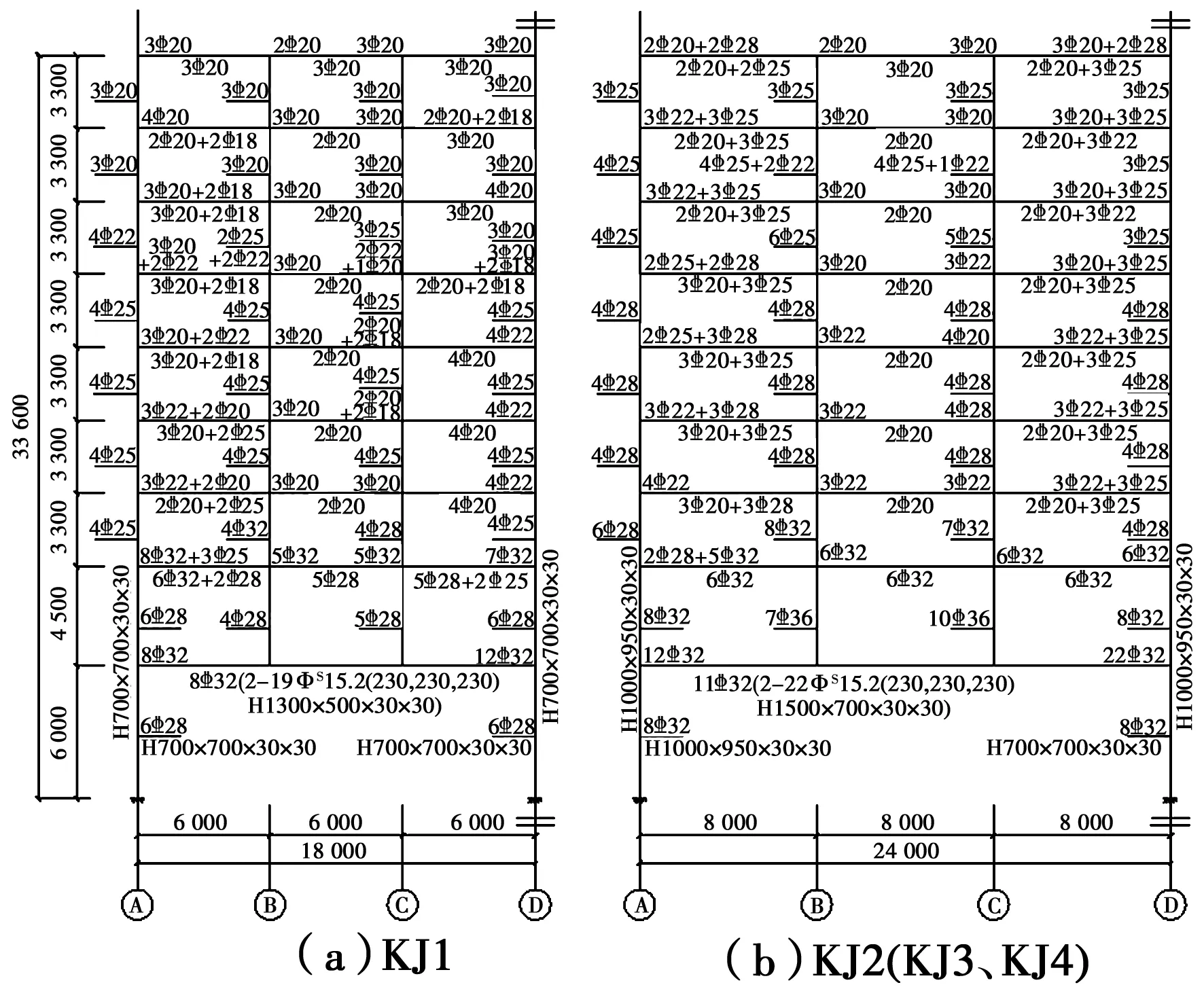
图2 结构配筋图Fig.2 Reinforcement of KJ1 and KJ2(KJ3、KJ4)

因受剪破坏不是研究重点，故当构件截面尺寸满足规范剪压比要求，且在按规范考虑“强剪弱弯”后箍筋配置合理时，即认为满足抗剪要求。

2 模型建立及地震波选取

2.1 模型建立

基于OpenSEES有限元分析平台，对竖向、水平地震共同作用下的平面模型进行弹塑性时程分析。模型建立中，梁、柱采用了纤维杆系模型，考虑楼板翼缘作用和柱脚钢筋粘结滑移。混凝土采用concrete02本构模型，滞回关系采用Berkeley两折线模型；非预应力钢筋及型钢采用steel02本构模型，预应力筋采用Hysteretic本构模型；采用Bond_SP01滑移模型考虑柱脚位置处钢筋与混凝土间的粘结滑移[12-13]。

在模拟分析中，预应力筋采用“两阶段工作原理”考虑[14-15]：第1阶段为张拉施工阶段，预应力作用相当于“荷载”，即预应力筋的有效预应力σpe提供等效荷载；第2阶段为张拉灌浆后的使用阶段，预应力筋相当于普通钢筋，只是其抗拉强度设计值取fpy-σpe。因而，预应力混凝土结构构件就可以视为一个承担外荷载和预应力等效荷载的“普通钢筋混凝土结构构件”，其中，预应力筋材料强度为fpy-σpe。

2.2 地震波选取

弹塑性时程分析地震波选自PEER地震波数据库，同时，考虑水平及竖向地震作用，对各算例分别选取7对实际地震波记录。

首先，对PEER数据库水平分量地震波进行初筛，然后采用双频段控制选波，双频区段为[0.1 s,Tg]及[T1-0.15 s,T1+0.15 s]，控制其加速度与规范反应谱值的误差不超过15%。在选取水平分量地震波的同时，取对应的竖向地震波记录。在对竖向地震波进行加速度峰值调幅时，分别取竖向与水平地震加速度峰值比V/H=0、0.65、1.2，如表4所示。

3 结果分析

3.1 破坏准则

3.1.1 整体失效的判定

1)在结构的任何一层中，所有竖向构件上下端均出现塑性铰，即所谓的层侧移机制，且层间位移角大于2%。

2)任何一层的层间位移角超过3%。

3.1.2 局部失效的判定 构件塑性铰转动需求大于其转动能力，具体表现为塑性铰截面混凝土最大压应变小于极限压应变。

3.2 KJ1和KJ3罕遇地震分析

算例KJ1、KJ3为跨度不同的基本算例，H/V均为0.65，旨在研究PSRC空腹桁架转换层框架结构的基本抗震性能和结构响应特征。对算例KJ1、KJ3进行8度罕遇地震下的弹塑性时程分析，KJ1输入地震波w1～w7、KJ3输入地震波w8～w14。

3.2.1 侧向位移 图3和图4分别列出了算例KJ1、KJ3在各自7对地震波下层侧向位移的最大值和最大值的平均值(简称平均值，下同)。

由图3、图4可见，算例KJ1、KJ3侧向位移曲线整体均未呈现出普通框架的剪切型，而是在转换层处出现明显改变。与剪切型侧移曲线相比，KJ1、KJ3的转换层及其下部楼层侧向位移明显减小，这源于设计时对结构转换层及下部楼层的抗侧刚度的加强。

图4 KJ3层侧向位移最大值Fig.4 Maximum lateral displacement of KJ3

3.2.2 层间位移角 图5和图6分别列出了算例KJ1、KJ3在各自7对地震波下层间位移角的最大值和最大值的平均值。

计算结果表明，KJ1与KJ3的层间位移角最大值分别为1/79和1/71，平均值分别为1/87和1/98，未见整体失效，且有较大富余。由图5、图6可见，转换层及其下部楼层的层间位移角远小于上抬框架各层，且未出现明显的塑性变形，这与层侧向位移的变化是一致的。此外，两算例层间位移角最大值的平均值均出现在第7层，这与第7层柱截面尺寸减小相关。

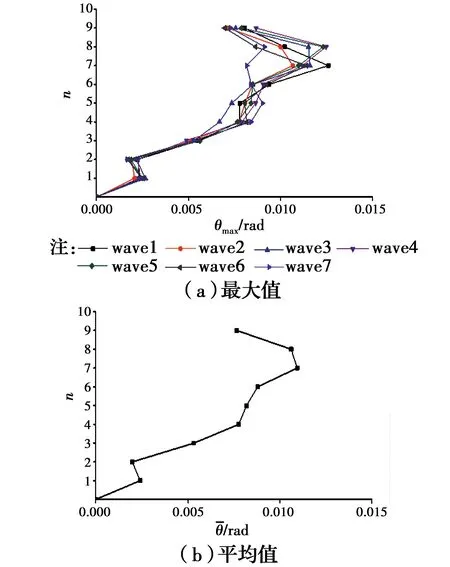
图5 KJ1层间位移角最大值Fig.5 Maximum story drift of KJ1

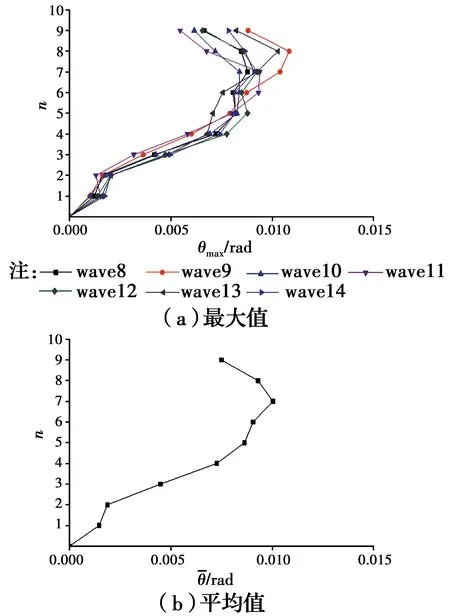
图6 KJ3层间位移角最大值Fig.6 Maximum story drift of KJ3

3.2.3 转换层竖向位移 PSRC空腹桁架转换层结构转换跨度大，对竖向地震作用更为敏感。如果桁架转换层出现较大竖向位移，将对转换层及其上部构件受力产生影响。在预应力、竖向荷载以及水平与竖向地震共同作用下，算例KJ1、KJ3转换层下弦梁跨中竖向位移最大值计算结果见表5。转换层下弦梁如图7所示，位移向下为正。

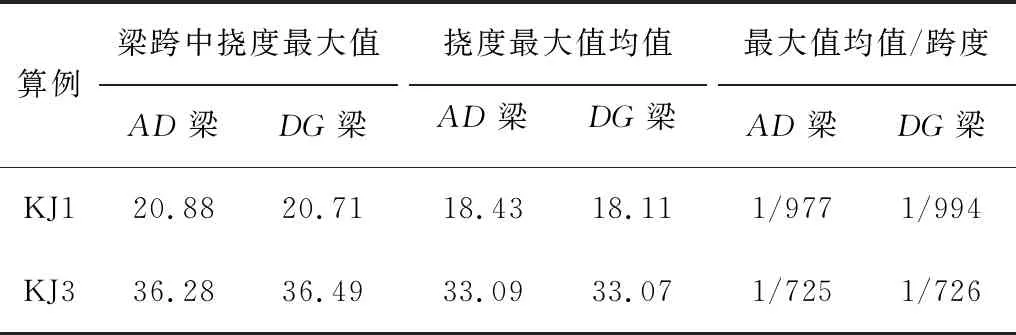
表5 桁架下弦梁跨中挠度Table 5 Deflection of the lower chord of transfer truss mm

图7 桁架下弦梁节点号Fig.7 Node number of the lower chord of transfer truss

参照《组合结构规范》(JGJ 138—2016)[16]，在正常使用极限状态，转换梁下弦挠度与计算跨度之比限值为l0/300(KJ1、KJ3对应为60、80 mm)，且不宜超过l0/400(KJ1、KJ3对应为45、60 mm)。由表4可见，梁跨AD与DG的数值基本相等，且与规范JGJ 138—2016的要求相比有明显富余。

3.2.4 塑性铰分布 考虑算例KJ3与KJ1计算结果类似，故仅给出算例KJ1在7对地震波下的塑性铰分布图，见图8，空心圆代表截面上下部单向出铰，实心圆代表双向出铰。

根据计算分析结果，总结KJ1和KJ3塑性铰分布特点为：

1)转换柱。转换层及其下部楼层的转换柱多在转换桁架下弦梁相连的边节点处首先出铰，转换柱虽难以避免出现塑性铰，且少数地震波下出铰数较多，但塑性铰转动需求远小于上抬框架梁。

2)桁架上、下弦梁和腹杆。下弦梁未见出铰、上弦梁仅个别出铰，中腹杆部分出铰，塑性铰转动需求远小于上抬框架梁。

3)上抬框架柱。与转换层上弦梁相连的3层柱底有部分出铰，塑性铰转动需求远小于上抬框架梁；其他上抬框架柱部分出铰，转动需求明显小于上抬框架梁。

4)上抬框架梁。上抬框架梁出铰明显最多，且转动需求明显最大。除顶层外其他各层普遍出铰，4～7层塑性铰转动需求明显更大。上述特点表明，上抬框架符合“强柱弱梁”设计原则，实现了以梁铰为主的混合出铰耗能机制。

图8 KJ1塑性铰分布Fig.8 Plastic hinge distribution of KJ1

综上所述，转换柱、空腹桁架下弦梁是作为最后一道防线的关键构件，虽然不能避免转换柱出铰，但塑性铰转动需求小，得到较好地保护；桁架上弦及其相连的上抬框架柱，以及桁架的中腹杆作为中间过渡防线虽有部分出铰，但转动需求小，未见明显损伤；结构塑性铰主要集中在上抬框架梁，并以此耗散地震能量。由此可见，两算例均可以满足“强转换”、“多道防线抗震设防”和上抬框架“强柱弱梁”等设计基本原则，具有较好抗震性能。

3.2.5 关键杆件塑性铰转动需求 表6列出了算例KJ1、KJ3(H/V=0.65)各类构件塑性铰的转角延性需求，其延性需求均在合理范围内；同时，计算结果表明罕遇地震下各出铰截面混凝土受压应变均未达到极限压应变值，即不出现局部破坏。

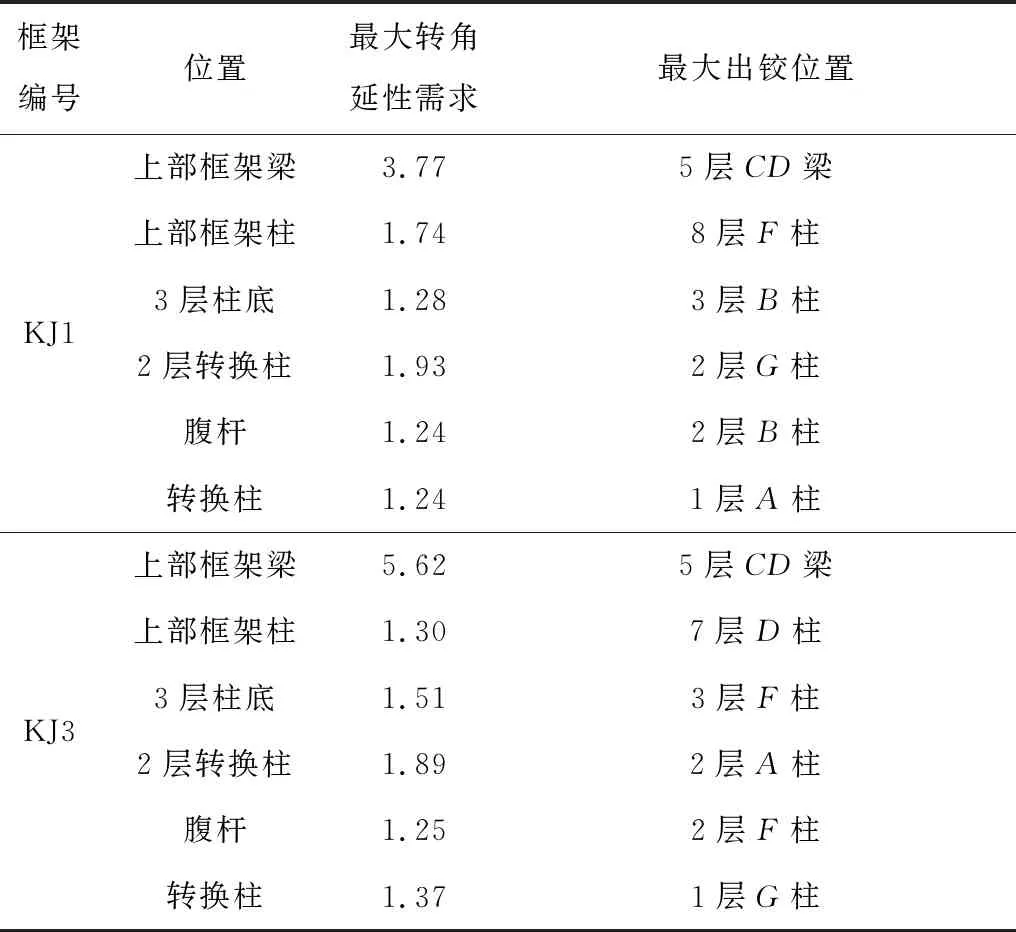
表6 构件最大转角延性需求Table 6 Maximal rotational ductility requirement of elements

3.3 KJ3极罕遇地震分析

结构有可能遭遇超越罕遇地震水准的地震作用，在此种情况下，若PSRC空腹桁架转换结构在最后一道防线出现破坏，其结果将是灾难性的，危害程度远大于普通框架结构。为确保该类结构在超越罕遇地震水准后的安全储备，以及为进一步研究可能出现的破坏模式，现以算例KJ3为对象，进行8度极罕遇地震水准下的弹塑性时程分析。

按照《中国地震动参数区划图》(GB 18306—2015)的定义，极罕遇地震相应于年超越概率为10-4的地震动，其PGA取基本地震动时的2.7～3.2倍。8度设防基本地震动峰值加速度为200 cm/s2，对应的极罕遇地震动水准下则为640 cm/s2。故算例KJ3在极罕遇地震下的弹塑性时程分析时，需将w8～w14地震动水平分量峰值加速度调整到极罕遇地震动水准，竖向分量仍按V/H=0.65的比例确定。

3.3.1 层间位移角 计算结果表明，KJ3最大层间位移角值在1/76～1/40之间，最大层间位移角值平均值为1/54，位于上抬框架上部的6～8层。其中，在地震波w11下层间位移角在上抬框架中达到最大值1/40，对应的底层和转换层层间位移角分别为1/298和1/333，数值明显较小。

综上所述，在极罕遇地震下，最大层间位移角虽然接近3%的限值，但没有形成层侧移破坏机制，未出现整体破坏，且转换层及其下部楼层层间位移角小，得到了较好的保护。

3.3.2 塑性铰分布 算例KJ3在w11作用下层间位移角反应最为显著，在图9中给出其塑性铰分布，通过与罕遇水准下塑性铰分布图的对比，总结PSRC空腹桁架转换层框架结构在极罕遇地震作用下的塑性铰分布的特点。

1)转换柱。边转换柱的底端新增出铰，所有塑性铰转角需求仍较小。

2)上弦梁、下弦梁和中腹杆。上弦梁端和中腹杆底端出铰更为普遍，但转动需求小；下弦梁不出铰。

3)上抬框架柱。上抬框架柱塑性铰数量增加，塑性铰转动需求增大趋势也较为明显。其中，转换桁架上弦梁紧邻的3层柱下端普遍出铰，且部分塑性铰转动需求相对较大。

4)上抬框架梁。除顶层外，上抬框架梁端截面几乎全部出铰，且转动需求明显大于其他构件。

综上所述，KJ3在极罕遇地震作用下临近破坏时，转换层及其下部楼层塑性铰转动仍较小，后续防线得到较好保护。上抬框架混合出铰明显，地震能量的耗散仍主要依靠上抬框架梁进行，多道防线抗震设防的设计思想得以实现。需说明的是，为解决个别地震波下转换柱出铰数略多的问题，必要时可适当提高转换柱的承载能力。

4 地震动竖向分量影响分析

4.1 侧向位移

算例KJ2、KJ3和KJ4水平与竖向地震动加速度峰值比V/H分别为0、0.65和1.2，其在各自7对地震波作用下侧向位移最大值的平均值分布如图10所示。由图10可见，不同V/H水平下，侧向位移曲线几乎重合，这说明地震动竖向分量的改变几乎未对该类结构的侧向位移产生影响。

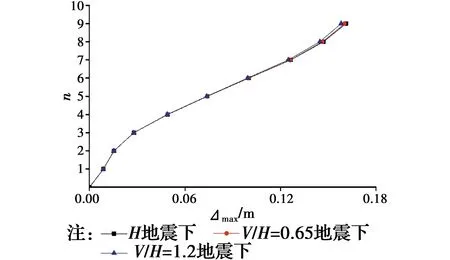
图10 结构侧向位移曲线Fig.10 maximum lateral displacement of KJ2-KJ4

4.2 中腹杆下端节点位移

在算例各自7对地震波下，空腹桁架下弦各控制点(图7)竖向位移最大值见表7。由表7可见，随着地震动竖向分量的增加，转换桁架下弦各控制点(B、C、E、F点)竖向位移最大值也随之增大，其中，靠近边转换柱的B、F节点竖向位移增大尤为显著。以C节点处竖向位移最大值平均值为例，KJ4与KJ3相比，增大25.6%；KJ4与KJ2相比，增大60.4%。KJ4在个别地震波作用下C节点竖向位移已达到44.9 mm。随着V/H的增加，各控制节点的竖向位移不均匀性加大，导致类似支座不均匀沉降效应，这将对上部构件造成相应的影响，如内力重分布更为显著、构件提前开裂等问题，应予以重视。

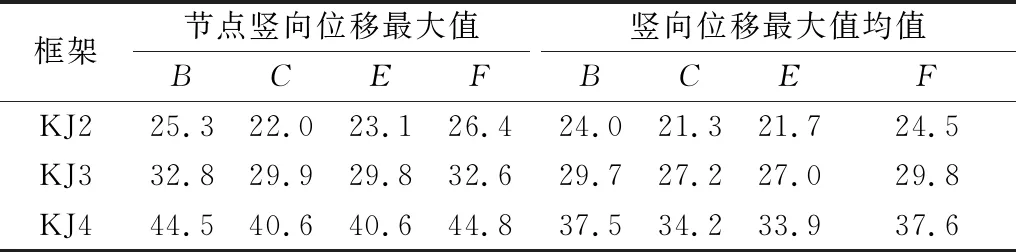
表7 转换层下弦梁竖向位移Table 7 Vertical displacement of the lower chord of transfer truss mm

4.3 塑性铰分布

算例KJ2～KJ4在w8地震波下塑性铰分布具有代表性，见图11。总结塑性铰分布随竖向地震动增大的发展规律如下：

1)转换柱。随着V/H数值的增大，转换柱塑性铰数量增多，由边转换柱与空腹桁架下弦梁相交节点处下柱端出铰，逐步向边转换柱与空腹桁架下弦梁相交节点处上下柱端出铰、底层边转换柱下端出铰扩展；同时，塑性铰转动需求呈现增大趋势，但转动需求仍很小。

2)上弦梁、下弦梁及中腹杆。随V/H的增大，空腹桁架下弦仍未出铰；上弦梁出铰数量增多，且呈现由梁端向中部发展的趋势，当V/H=1.2时，上弦梁出铰数量已较为普遍。

3)上抬框架塑性铰。转换桁架上抬框架梁充分出铰，随着竖向分量占比增加，部分梁塑性铰由单向铰变化为双向铰，且转动需求也有一定增加。而上部框架柱受竖向分量影响相对较小。

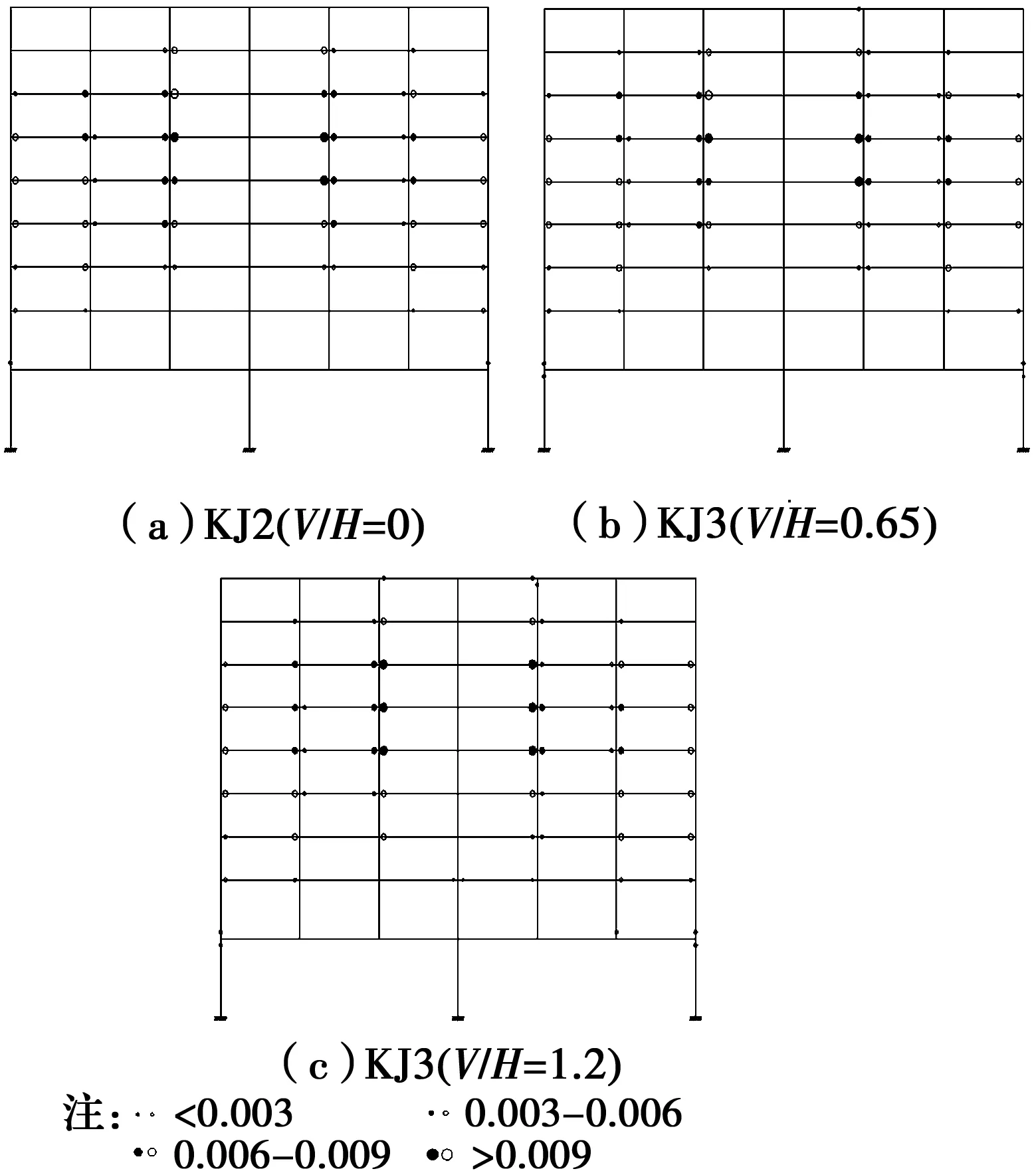
图11 KJ2～KJ4塑性铰分布(w8)Fig.11 Plastic hinge distribution of KJ2～KJ4

5 结论

1)在“强转换”设计原则基础上，提出了多道防线划分和内力调整的具体方法。多道防线包括：首道防线为转换层上抬框架梁柱(不包括与桁架上弦梁紧邻的上层框架柱)；其次为空腹桁架中腹杆、上弦梁和与其紧邻的上层框架柱；桁架下弦梁和转换柱则作为最后一道防线。

2)罕遇地震水准下，考虑竖向与水平地震共同作用，按多道防线设防思想设计的PSRC空腹桁架转换层框架结构不出现整体和局部破坏，形成以首道防线上抬框架梁铰为主的混合出铰耗能机制，结构多道防线设防思想总体得以实现。

3)极罕遇地震水准下结构层间位移角明显增大，但不出现整体破坏，仍形成以上抬框架梁铰为主的混合出铰耗能机制，表现出较好的抗震性能。

4)随着竖向地震动的增大，其影响主要表现在桁架下弦挠度显著增加，当竖向地震动较大时，其对上抬构件内力的附加影响应予以考虑。

需要说明的是，底部增设落地剪力墙将明显改善PSRC空腹桁架转换框架结构底部的抗侧刚度比和大震下的抗震能力，提高该类结构的可靠性。本文采用平面模型进行抗震性能研究，后续将进一步补充空间模型的研究，包括增设剪力墙的影响。