中间包钢液流动行为的数值模拟及控流装置优化

常庆明，吕 言，许芳宇

(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081)

中间包作为连铸生产的重要环节，是连接钢包和结晶器的过渡型反应器，是由间歇式操作转向连续式操作的衔接点。随着连铸技术的发展，其作用除了储存和分配钢包钢液外，还可以通过控流装置来调整中间包内钢液的流动状态，以达到维持钢液温度稳定和净化钢液的目的。由此可见，中间包控流装置如挡墙、堰坝、湍流控制器等的合理设计，是提升中间包冶金效果(例如改善中间包内钢液流动状态、延长钢液在中间包内停留时间、增加夹杂物上浮率及减少钢液卷渣等)的关键所在[1-3]。

目前，冶金工作者通常采用物理模拟实验、现场采样及数值模拟等方法来研究中间包内钢液的流动行为。物理模拟手段主要是通过建立等比例中间包水模型并随后加入示踪剂的方法测定流体平均停留时间分布(RTD)曲线[2-4]，以此来优化控流装置，但该方法具有局限性，实验结果不可避免地受到仪器精度及人为扰动等因素的影响。而中间包冶金过程涉及工厂高温作业，采用现场直接测量方法难度大、危险系数高，测定数据反而不理想。数值模拟则是基于计算流体力学方法，利用有限元模拟软件如FLUENT、CFX、PHOENICS等对中间包内钢液的流动行为进行仿真分析，近些年，随着模拟计算精度的不断提高，该方法在冶金领域已得到广泛应用[5]。

某钢厂T形四流方坯连铸机自投产以来，铸坯夹杂物含量一直处于较高水平，观察发现，非稳态浇注时铸坯质量明显低于稳态浇注的情况，这会影响到后序钢坯在结晶器中连铸生产的洁净度。钢包更换钢液时，中间包在长水口没有持续钢液补充但生产不能停止的情况下，还要保证拉坯速度恒定且不影响铸坯质量。而换钢包时熔池液面下降，钢-渣界面波动会导致中间包内钢液的流动状态发生变化，进而影响拉坯质量。该过程多次出现在完整浇注进程时，必然会对铸坯质量控制造成不利影响。基于实践经验，研究者已对该中间包控流装置进行了改进，铸坯中夹杂物含量有所降低，但仍存在各流一致性差、铸坯质量不稳定等问题。为此，本文采用数值模拟方法对该中间包流场进行计算，并对控流装置进行了进一步优化，在此基础上提出了相应的改进方案。

1 数学模型

1.1 几何模型

本研究以某钢厂的T形四流大方坯连铸机中间包为原型，该中间包容量为50 t，浇注时间周期为30 min，工作液面为800 mm，浇注钢种以20MnSi为主，主要参数见表1。中间包内腔结构示意图如图1所示，考虑到结构对称性，为缩短计算时间，特取其一半作为研究对象。图1(a)中，1#和2#分别表示一流出流口和二流出流口，半径均为25 mm，图1(b)为湍流控制器的结构示意图。对应中间包的三维几何模型及网格划分如图2所示。为在保证模型精度的同时缩短计算时间，本文采用非均匀结构化网格对模型进行划分，即入口、出口和湍流抑制器采用较密的网格划分，其他区域则采用较稀疏的网格划分，网格总数约为280 000。

表1 中间包工艺参数

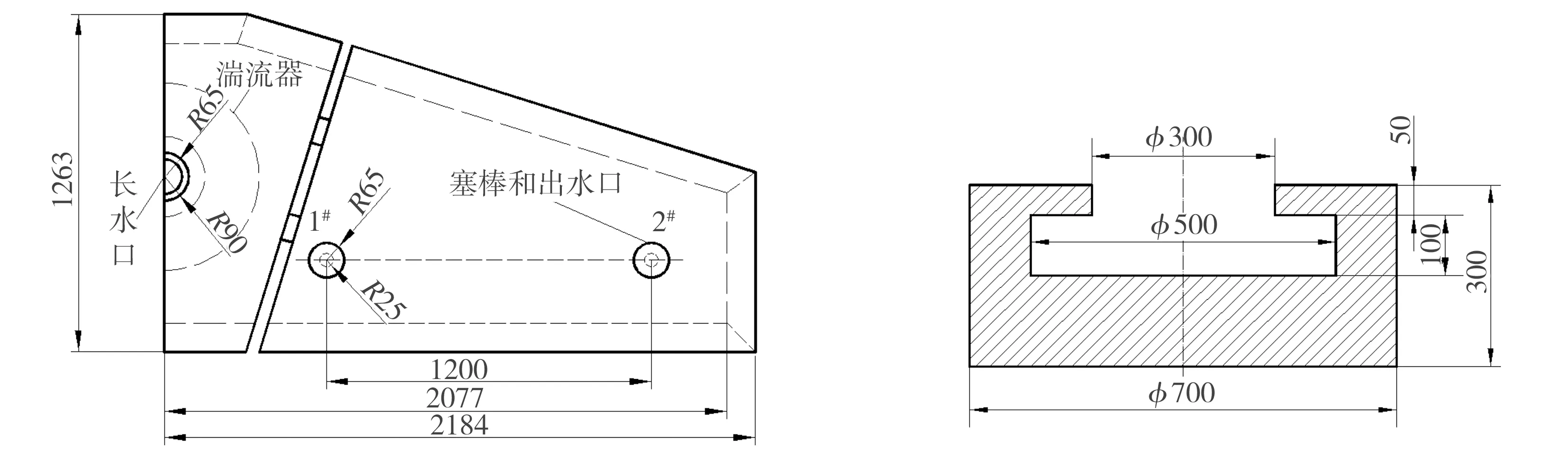
(a)原型中间包

(b)湍流控制器

图1 原型中间包及湍流控制器尺寸

Fig.1 Prototype tundish and turbulence controller dimensions

(a)几何模型

(b)网格划分

图2 原型中间包的几何模型和网格模型

Fig.2 Geometric model and grid partition of prototype tundish

1.2 基本假设

本文对钢液在中间包内的流动行为作如下假设：①中间包内流体流动为三维不可压缩稳态湍流流动；②中间包液面为自由表面，不考虑中间包覆盖渣和液面波动，不考虑温度场的影响，并假设自由表面为自由滑移壁面；③夹杂物含量低，不考虑其对流场的影响；④示踪剂传输为非稳态传质过程；⑤钢液的密度、黏度、比热容等物理参数为常数。

1.3 控制方程

描述中间包内气-液两相流动基本方程为[6]：

连续性方程

(1)

动量方程(Navier-Stokes方程)

(2)

湍动能方程(κ方程)

(3)

湍动能耗散方程(ε方程)

(4)

示踪剂在中间包传质方程

(5)

式中：ρ为流体密度，kg/m3；ui和uj分别为湍流时均速度和脉动速度，m/s；μeff为湍流有效黏性系数，kg/(m·s)；p为压力，Pa；gi为重力加速度，m·s-2；μt为湍流黏性系数，kg/(m·s)；κ为湍动能，m2/s2；Gκ为由平均速度梯度产生的湍动能，m2/s2；ε为湍动能耗散率，m2/s3；cs为示踪剂浓度，kg/m3；Ds为示踪剂扩散系数，m2/s；C1、C2、Cμ、σκ、σε为经验常数，本文采用Launder和Spalding推荐数据，C1=1.44，C2=1.92，Cμ=0.99，σκ=1.3，σε=1.0。

1.4 边界条件

结合中间包实际流动情况，四流大方坯连铸中间包模型的边界条件设置如下：

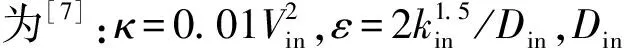
(2)钢液出口设置为速度出口，体积流率均为0.5。

(3)中间包液面为自由表面，剪应力为零；在示踪剂模型中，示踪剂物理性质与钢液相同，所有壁面均采用零浓度梯度。

(4)示踪剂质量分数入口边界条件为：当t≤1 s时，示踪剂摩尔浓度设为1；t>1 s时，示踪剂摩尔浓度设置为0；出口边界设置监视面，监视各时刻示踪剂的摩尔质量浓度。

1.5 钢液流动特性分析

为了绘制RTD曲线，需在钢液入口处加入示踪剂。首先对中间包流场进行计算，当稳态流场收敛后，在钢液入口加入示踪剂瞬态计算1 s，然后停止示踪剂加入，继续瞬态计算2500 s后，求解三维湍流传质方程，即算出各流出口的示踪剂浓度随时间的分布(RTD)曲线。中间包流场一般认为由活塞区、死区和混流区三部分组成。浇注过程中，死区过大会造成钢液流动性降低，有效体积减少，而活塞区过小则不利于中间包温度的均匀分布。结合实际生产情况，本文特选取Sahai等[8]提出的模型对模拟计算所得RTD曲线进行分析：

稳态流场钢液的理论平均停留时间τ

τ=V/Q

(6)

(7)

t′c—

(9)

(10)

式中：V表示中间包正常工作的钢液体积，m3；i为时间步；j为出流口编号，j=1表示第一出流口，j=2表示第二出流口；ti为取样时刻，s；Δt为测量时间间隔，s；ci为ti时刻对应示踪剂的浓度，kmol/m3。

死区体积分数Vd

(11)

活塞区体积分数Vp

Vp=(tmin+tmax)/2τ

(12)

全混区体积分数Vm

Vm=1-Vd-Vp

(13)

式中：tmin表示最小滞留时间(示踪剂响应时间)，亦即活塞区中示踪剂流过最短路程所需时间，检测时示踪剂浓度值达到1%的时间定义为tmin，s；tmax表示出流口处示踪剂浓度达到最大值所需时间，也就是示踪剂在活塞区流过最大路程所需时间，s。

2 设计方案

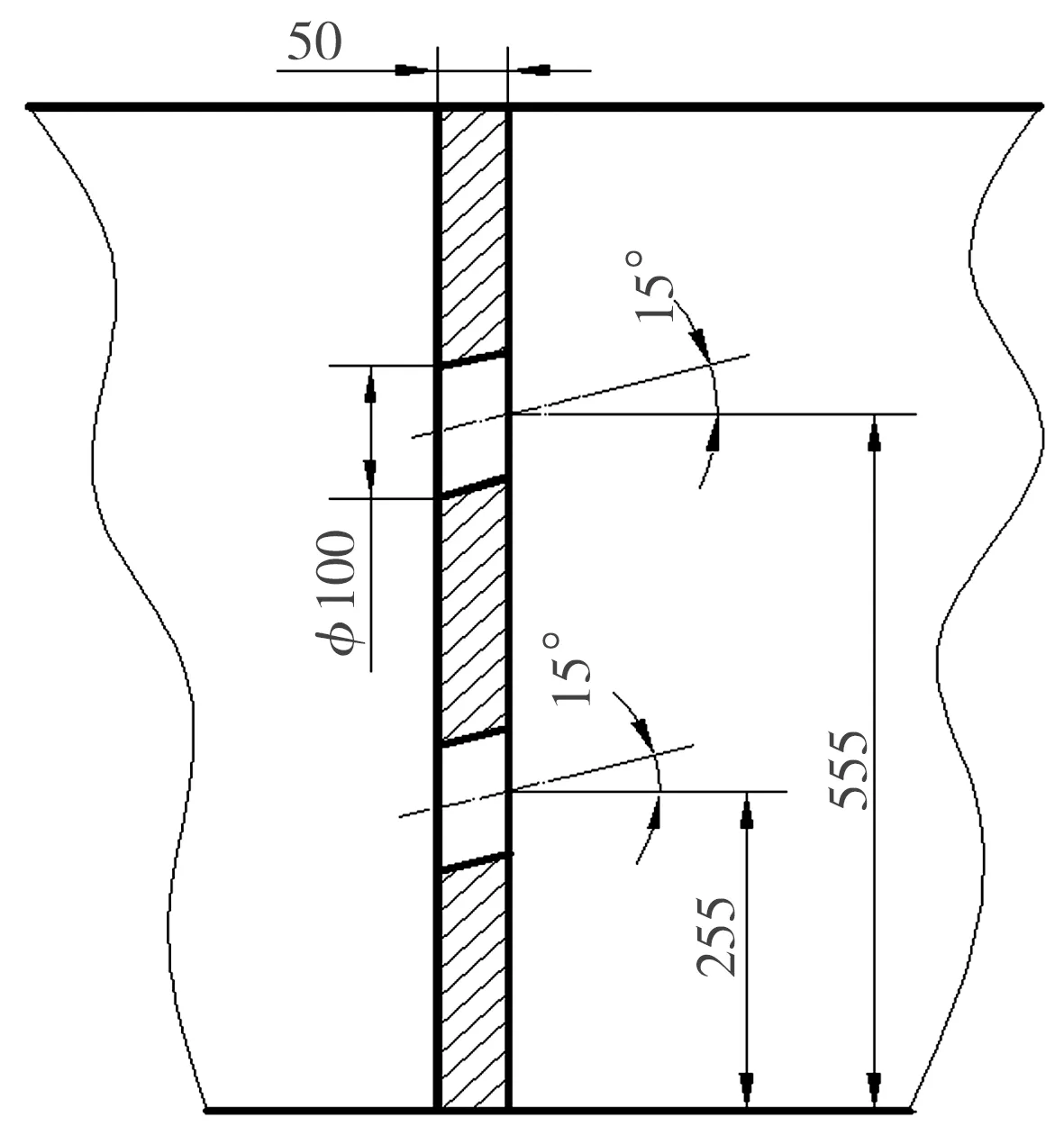
图3 原型导流孔的尺寸图

表2 中间包导流孔结构与尺寸的设计方案

Table 2 Design for the structure and dimensions of tundish diversion hole

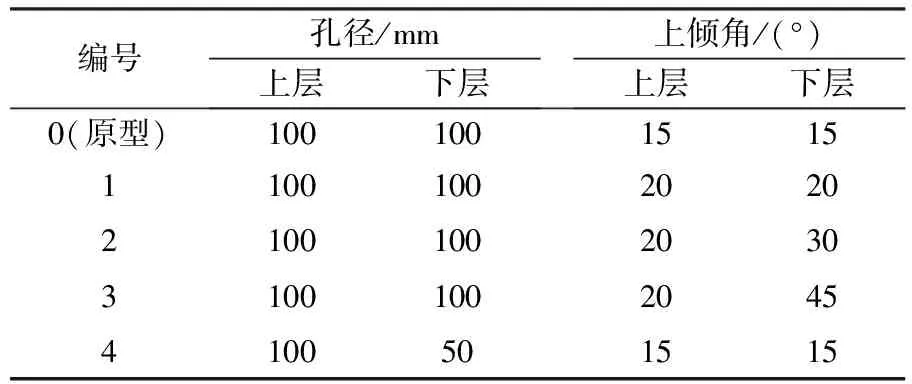
编号孔径/mm上层 下层上倾角/(°)上层下层0(原型)10010015151100100202021001002030310010020454100501515

3 模拟结果与分析

3.1 原型中间包流场分析

原型中间包服役过程中钢液流动行为的数值模拟结果如图4所示。图4(a)和图4(b)为原型中间包内通过塞棒和出流口中心截面处钢液的速度矢量分布和流线分布图，可以看出，钢液在长水口、导流孔及出流口速度非常快，整个中间包流线简单，钢液流线分布较不均匀。挡墙左侧流线较为密集，表明钢液流速快、湍动能高，为强湍流区，并且长水口周围形成向上环流，直接流向渣液层。这一强环流一方面可以将钢液中的渣滴带向渣层并且很可能被渣层捕获，从而起到除渣效果；另一方面，强湍动能的环流对中间包表面渣层的冲击可能将渣层冲开，使钢液裸露，与空气接触造成钢液二次氧化。挡墙右侧流线相对稀疏，钢液流速较缓和，湍流强度较低。同时还可以观察到，由强湍流区经导流孔流出的钢液一部分向上流动，与渣层接触可能起到捕渣效果，然后经由2#出流口流向结晶器；另一部分钢液尤其是下层导流孔流出的部分钢液，则直接或者经过很短的路径流向1#出流口进入结晶器，这部分钢液携带的渣滴在中间包停留时间很短，来不及上浮而直接进入结晶器，在连铸坯中形成夹渣，严重影响了连铸坯质量。另外，在中间包几个角落部位，流线非常稀疏甚至没有流线经过，表明这几处形成了死区，死区内钢液几乎无法流动，不利于夹渣的上浮，中间包有效体积减小。

这一现象也可由如图4(c)所示的RTD曲线来验证，由图4(c)可以看出，原型中间包中一流的响应时间、达到峰值浓度时间及平均停留时间均非常短，并且示踪剂浓度值远高于二流的峰值浓度，这势必会造成钢液夹杂物没有充分的时间上浮。另外，两组RTD曲线的重合性差，一流和二流的峰值时间及峰值浓度差别较大，其中峰值浓度差达到0.29，表明中间包各流的流动一致性差，整个中间包流动特性不佳。原型中间包死区和活塞区的体积分数依次为18.6%、26.1%，死区体积分数较大，而活塞区体积分数较小，这不利于发挥中间包的冶金功效。由此可见，一流是限制中间包冶金功效发挥的短板，若能延长一流的响应时间及平均停留时间，则可以较大地改善该中间包的冶金功效。

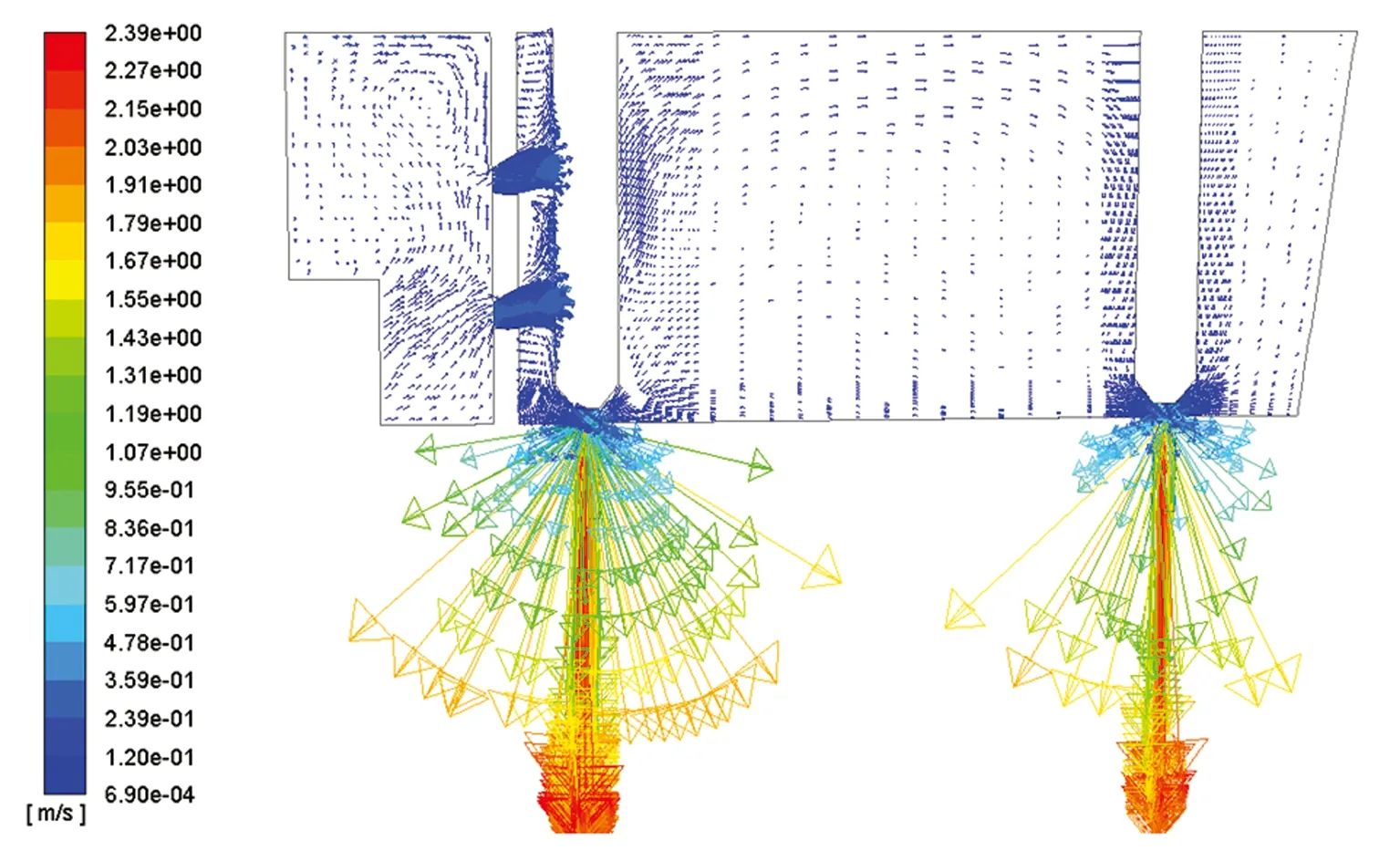
(a) 速度矢量图

(b) 速度流线图

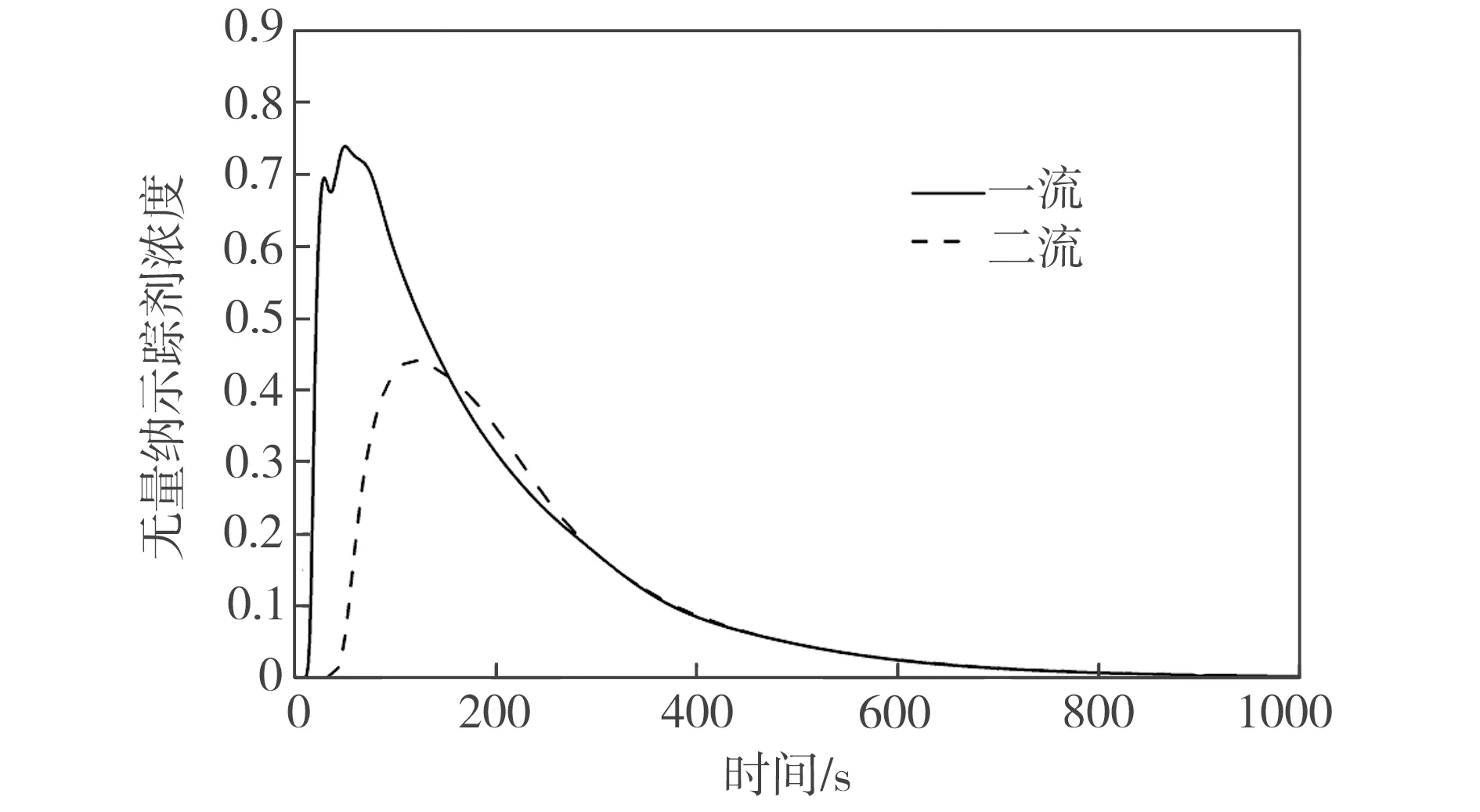
(c) RTD曲线

Fig.4 Numerical simulation results of flow behavior of molten-steel in prototype tundish

3.2 不同方案的流场分析结果比较

为改善原型中间包钢液流动特性不佳的问题，本研究采用了改变挡墙上导流孔结构以及增设坝结构的设计方法，并按照坝高、导流孔直径和上倾角的不同，设计了A0～A4、B0～B4共10种方案，方案编号中的字母代表两种不同的坝高(A对应坝高为200 mm，B对应坝高为300 mm)，数字代表5种不同的导流孔结构(与表2对应)。对10种方案条件下中间包内钢液的流动行为进行数值模拟，并绘制出对应的RTD曲线，结果如图5所示，对RTD曲线分析后得到各方案下钢液的流动特性数据列于表3中。

结合图5和表3可知，与原型中间包相比，改变导流孔倾角和增设坝结构能有效改善中间包内钢液的流动特性，大部分方案下中间包内各流响应时间有所延长，并且所有方案下一流响应时间长于原型中间包(均超过15.0 s)。除了B0方案外，其他9种方案下中间包内钢液的总平均停留时间均有所延长，特别是A1方案，其平均停留时间可达216.0 s，这有效降低了中间包短路流，有利于解决一流短路造成的夹渣物来不及上浮所引起的钢坯夹杂物含量超标问题；另外，各方案下活塞区体积相应增加了1.5%～38.3%，中间包死区体积降低了9.7%～29.0%，两流的峰值时间和峰值浓度差别均有所减小，表明各流的流动差异减小，中间包内钢液分配趋于合理，有利于各流之间钢液成分和温度的均衡。

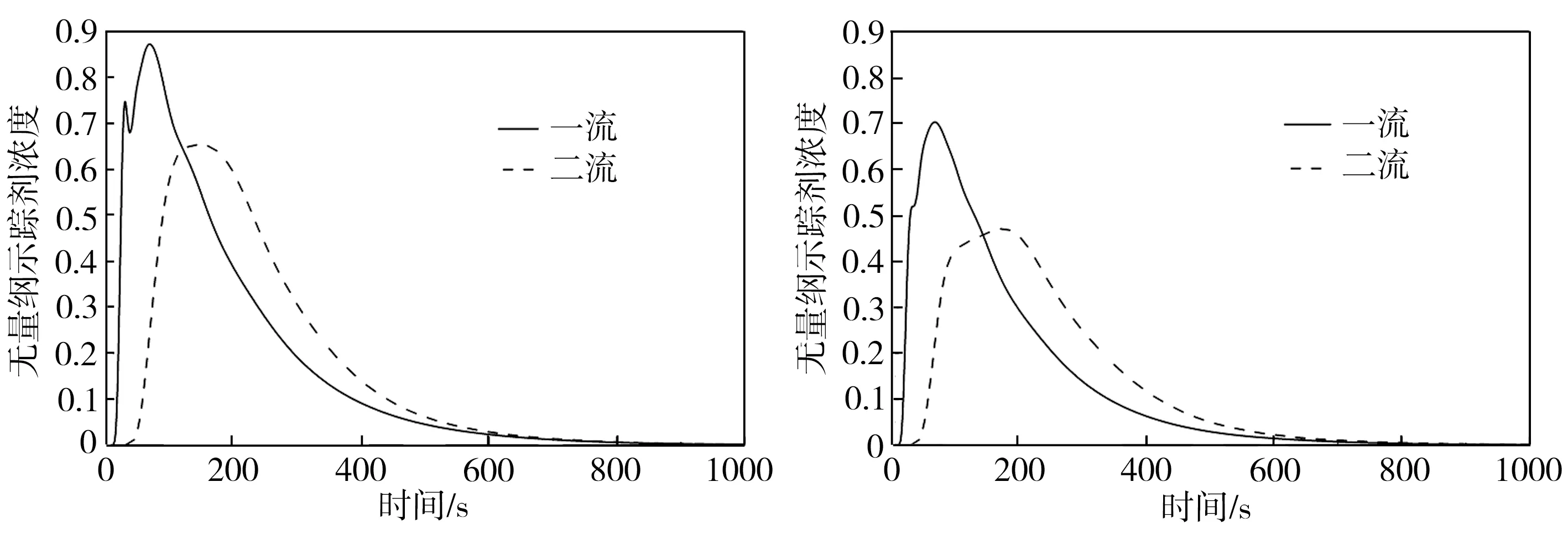
(a) A0方案

(b) B0方案

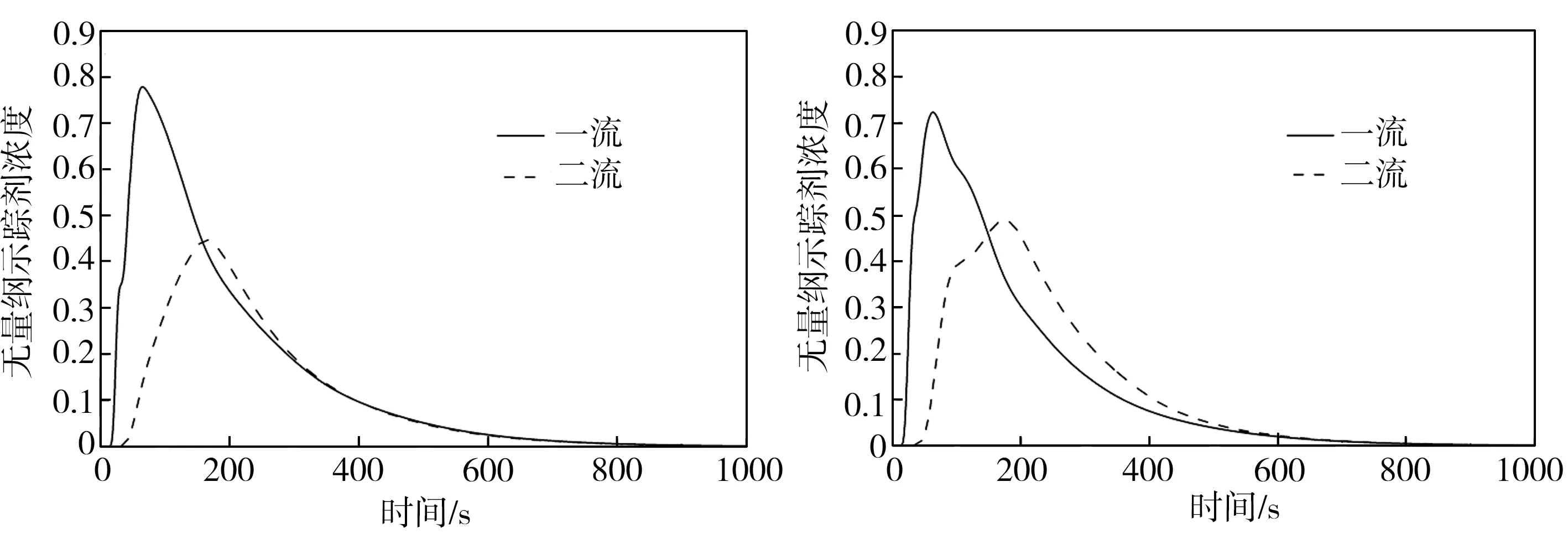
(c) A1方案

(d) B1方案

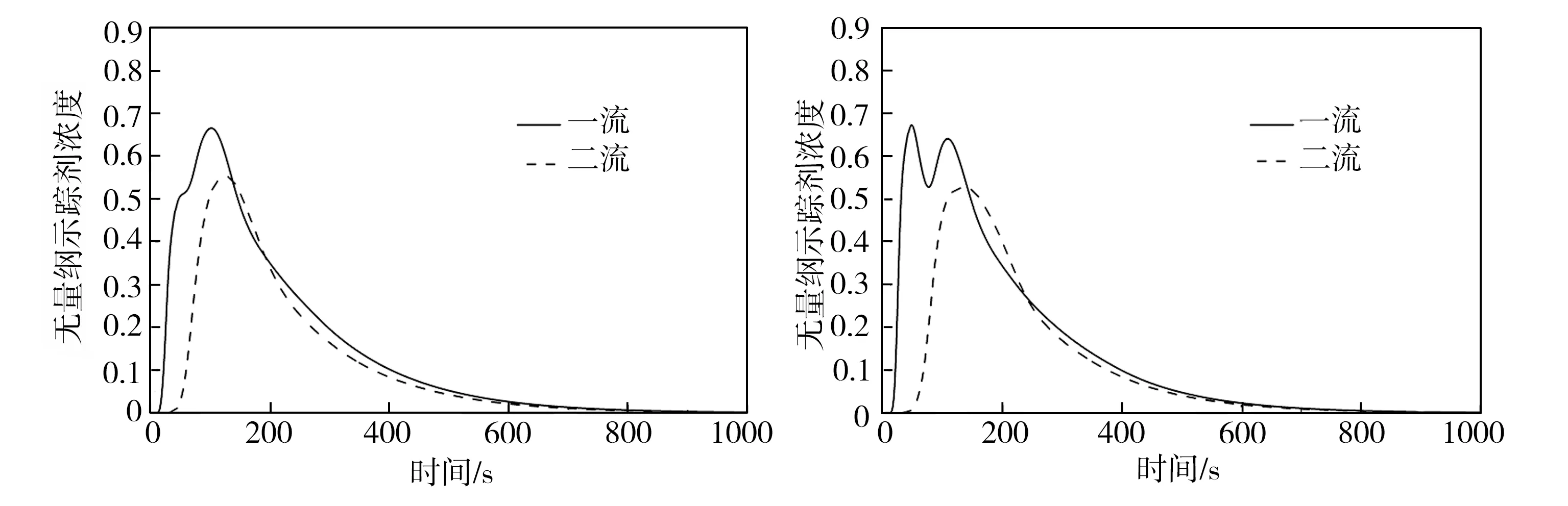
(e) A2方案

(f) B2方案

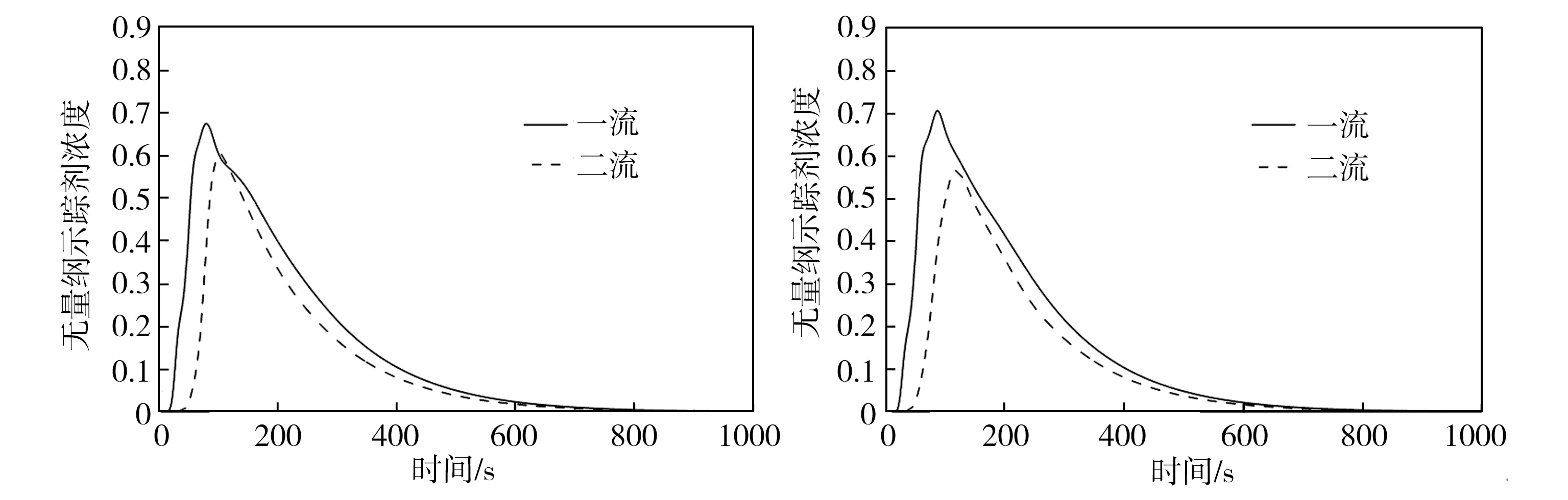
(g) A3方案

(h) B3方案

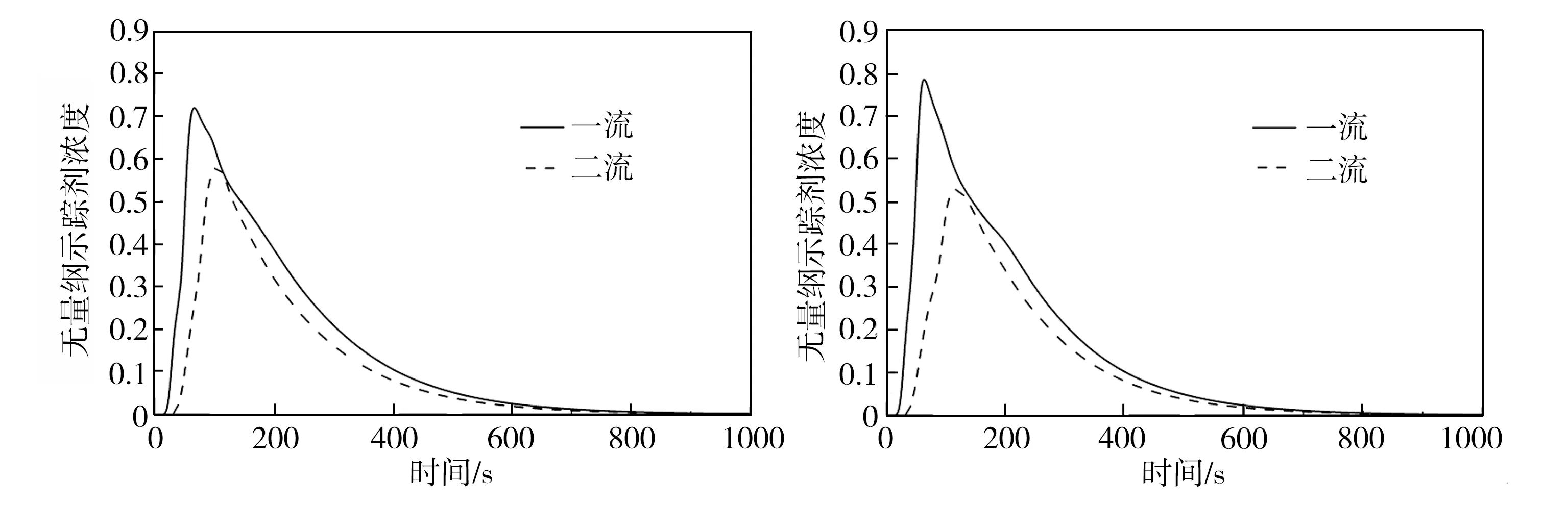
(i) A4方案

(j) B4方案

为探讨坝高对中间包内钢液流动特性的影响，将A0、B0方案的模拟结果与原型中间包进行比较(见图4、图5(a)和图5(b))，可以看出，在原型中间包结构基础上仅增设坝结构时，一流响应时间、停留时间及总体停留时间只有轻微变化，死区体积明显减小而活塞区体积显著增加，表明只设置坝高不能有效改善一流短路流问题。另外，将方案A1～A4的模拟结果与对应方案B1～B4的模拟结果比较后可知，在保持挡墙结构不变的情况下增加坝高，一流响应时间均略有缩短，二流响应时间有所延长，总停留时间稍有缩短，而死区体积分数降幅较大，混合区体积分数明显增加，这是因为坝设置在1#和2#出流口之间，故对处于坝前的1#出流口处的流场影响较小，对坝后区域的流场影响较大，增加坝高可使流向坝的钢液有更多部分向上流动，从而在中间包右侧形成较大的回旋流动，中间包右端角部死区体积减少。由此可见，增加坝高在一定程度上有利于提高中间包的冶金功能。

为分析下层导流孔上倾角对中间包内钢液流动行为的影响，将方案A1～A3与B1～B3依次进行对比后可知，在其他控流装置不变的情况下，当下层导流孔上倾角为30°时(与其为20°、45°时相比)，一流响应时间、平均停留时间、总平均停留时间最短，死区体积分数最大，活塞区体积分数最小，表明下层导流孔上倾角为30°的方案下中间包短路流现象最严重，不利于夹渣物上浮以及在中间包内形成良好的流场，不利于中间包冶金功能的提高。相较而言，当下层导流孔上倾角增至45°时，对应的各项指标最佳，最利于提高中间包的冶金功能。另一方面，随着下层导流孔直径的减少，一流响应时间及平均停留时间均有延长，总体平均停留时间也略有延长，且RTD曲线重合度更高，各流之间的流动状态更一致；但同时，减小下层导流孔直径后，中间包死区体积增加，活塞区体积减小，中间包冶金功效降低，这可能是因为下层导流孔直径和坝结构的协同作用反而导致中间包冶金效果变差。

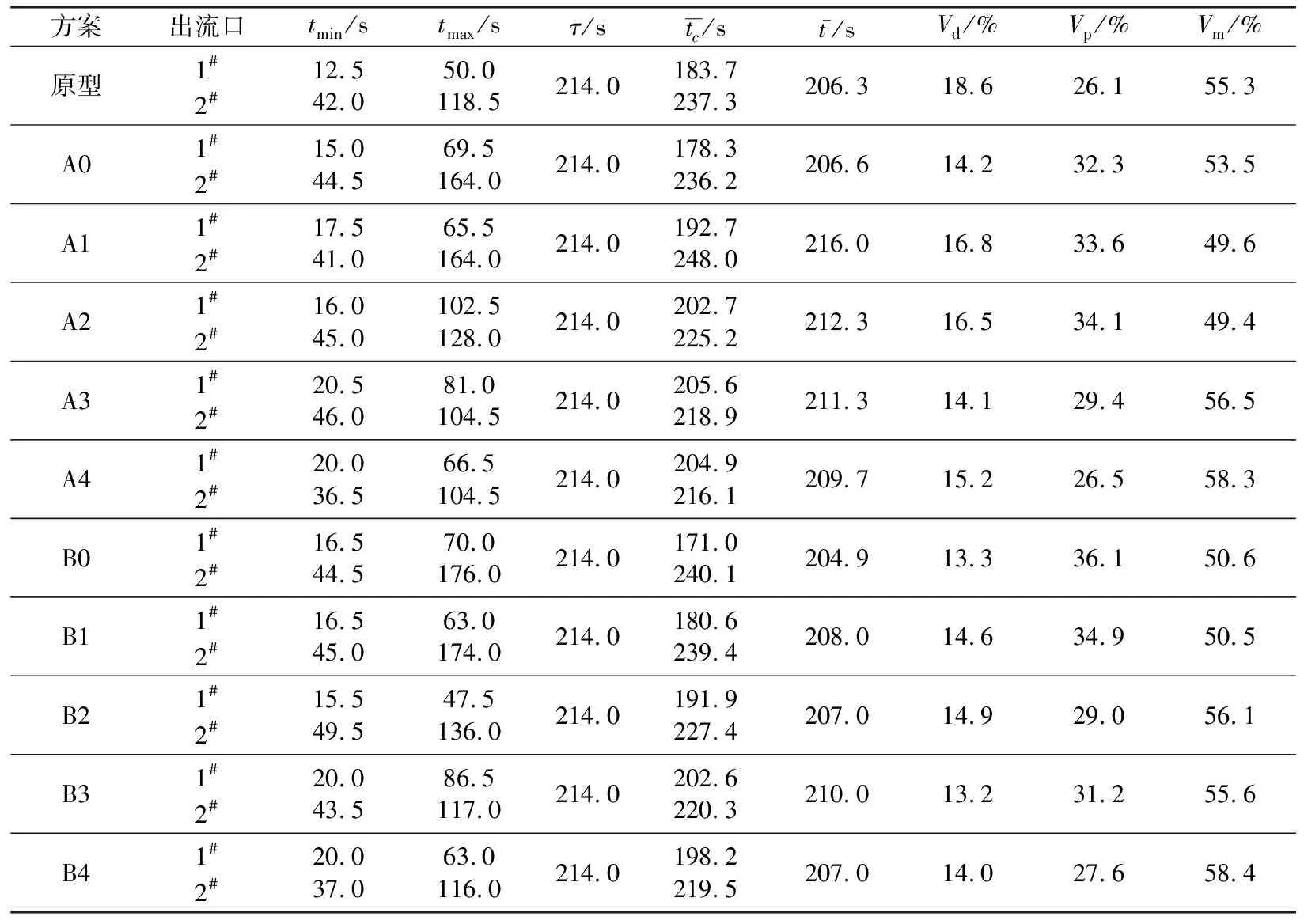
对10种改进方案综合分析后发现，A3、B3和B4方案均可使中间包内钢液获得较为理想的流动状态，且所有方案中B3方案相对最佳，相较于原型方案，中间包内钢液的平均停留时间增至210.0 s，死区体积下降了29%，活塞区体积增加了19.5%，一流和二流响应时间分别延长至20、43.5 s，改善了1#出流口附近的短路流现象；而A1方案的改善效果则相对最差。为此，对A1、B3方案条件下中间包内钢液的速度矢量分布和流线图进行分析，如图6所示。

由图6可见，一方面A1方案下层导流孔上倾角较小，有更多流体形成短路,直接从1#出流口流出，体现在RTD曲线上(见图5(c))则表现为一流浓度响应时间、峰值时间及平均停留时间较短；同时，由于坝高较低，经过坝结构的流体很难形成较大的多重循环流动。更为明显的是，与图6(d)相比，图6(c)右下角有较大区域无流线经过，表明该区域为死区，结合表4可知，采用A1方案模拟计算后中间包死区体积分数远大于采用B3方案的情况。综合分析，采用300 mm坝高、配合45°下层导流孔上倾角的导流系统，中间包内钢液流动特性最有利于钢液中渣质的去除，能充分体现中间包的冶金效果。

(a) A1方案，速度矢量分布

(b) B3方案，速度矢量分布

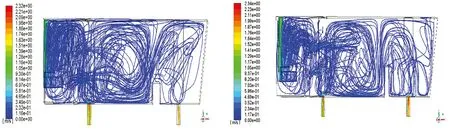
(c) A1方案，速度流线图

(d) B3方案，速度流线图

图6 不同方案对应的中间包内钢液速度分布云图

Fig.6 Velocity distribution diagrams of molten-steel in tundish under different schemes

4 结论

(1)原型中间包钢液流动易形成短路流，造成钢液中夹杂物来不及上浮，且各流流动状态差异较大、RTD曲线重合度较差，中间包流动特性不佳；此外，该中间包死区体积分数较大，活塞区体积分数较小，不利于中间包冶金功效的发挥。

(2)在中间包内增设坝结构，可以改善中间包内钢液的流动特性，且随着坝高增至300 nm，中间包右侧形成较大的回旋流动，死区体积分数减小，活塞区体积分数增大，有利于中间包冶金功效的提升。

(3)适当增大下层导流孔上倾角，在一定程度上可以延长一流出流响应时间，减弱中间包短路现象。另外，随着下层导流孔直径的减小，一流响应时间及停留时间延长，各流RTD曲线重合度及两流一致性有所改善，但中间包死区体积分数增大，活塞区体积减小。

(4)对于该T形四流大方坯连铸机中间包，最佳优化方案为坝高300 mm、上层及下层导流孔上倾角分别为20°和45°的B3方案，其对应的一流响应时间、中间包平均停留时间最长，各流的RTD曲线重合度高，死区体积分数相对最小。