胶结层含石英砂的黏钢加固混凝土界面黏结滑移本构关系研究

程海根，刘宇根，胡 晨，姜 勇，胡钧剑

(1.华东交通大学土木建筑学院，江西 南昌，330013；2.华东交通大学土木工程国家实验教学示范中心，江西 南昌，330013)

利用钢板加固钢筋混凝土结构时，常选用建筑结构胶或环氧树脂胶将钢板与混凝土粘贴，结构经加固后，其承载力主要取决于钢板-混凝土界面的黏结性能[1]。目前，针对钢板-混凝土界面黏结性能的研究大多基于黏结强度和黏结滑移这2种模型[2]，但根据黏结强度模型仅能确定结构的极限破坏承载力[3]，不能反映局部黏结界面的剥离破坏过程，而利用黏结滑移模型则能推导出整个界面剥离过程中的黏结应力与滑移量[4-8]。因此，黏结滑移本构关系不仅是有关钢板-混凝土界面研究的核心问题，也是建立相应有限元模型的基础。

石英砂是一种重要的工业矿物原料，作为矿物掺和料掺入后能在一定程度上提高基体材料的性能[9-12]。有鉴于此，本文将石英砂掺入结构胶中制备黏钢加固混凝土试件，借助双面剪切试验研究了钢板-混凝土界面的黏结滑移本构关系，并根据试验数据对已有黏结滑移模型进行修正。

1 试验

1.1 试验材料

混凝土设计强度等级为C40，实测其抗压强度为42.3 MPa；钢板为Q235热轧钢板，其抗拉强度为210 MPa、弹性模量为206 GPa、泊松比为0.25；黏结剂为杭州固安科技有限公司生产的JGN型建筑结构胶，其力学性能参数见表1；石英砂由新沂市宏润石英硅微粉有限公司提供，其粒度为45 μm、密度为2.65 g/cm3，主要化学成分见表2。

表1 JGN结构胶力学性能参数

表2 石英砂的化学成分(wB/%)

1.2 试验设计

设计7组钢板加固混凝土结构的试件，每组试件均包含2块150 mm×150 mm×300 mm的混凝土和2块900 mm×80 mm×4 mm的钢板，钢板、混凝土间的胶结层由JGN型建筑结构胶掺入不同量的石英砂均匀混合而成，7组试件胶结层的厚度以及其中石英砂与结构胶的体积比α列于表3。利用液压千斤顶及变形传感装置对试件的钢板-混凝土界面进行双剪切试验[13-14]，试件加载装置示意图及测试现场照片如图1所示。由图1可见，1组钢板加固混凝土结构试件中存在4个黏结面即剪切面，借助变形传感器测量2块混凝土间的相对滑移，以钢板加载端为起始位置，在中线沿加载方向距加载端5、25、45、75、115、165 mm处依次使用3 mm×2 mm规格的纸基电阻式应变片(电阻值为120±0.1 Ω)布置测点以记录黏结界面上钢板的应变分布，测点布置方案见图2。

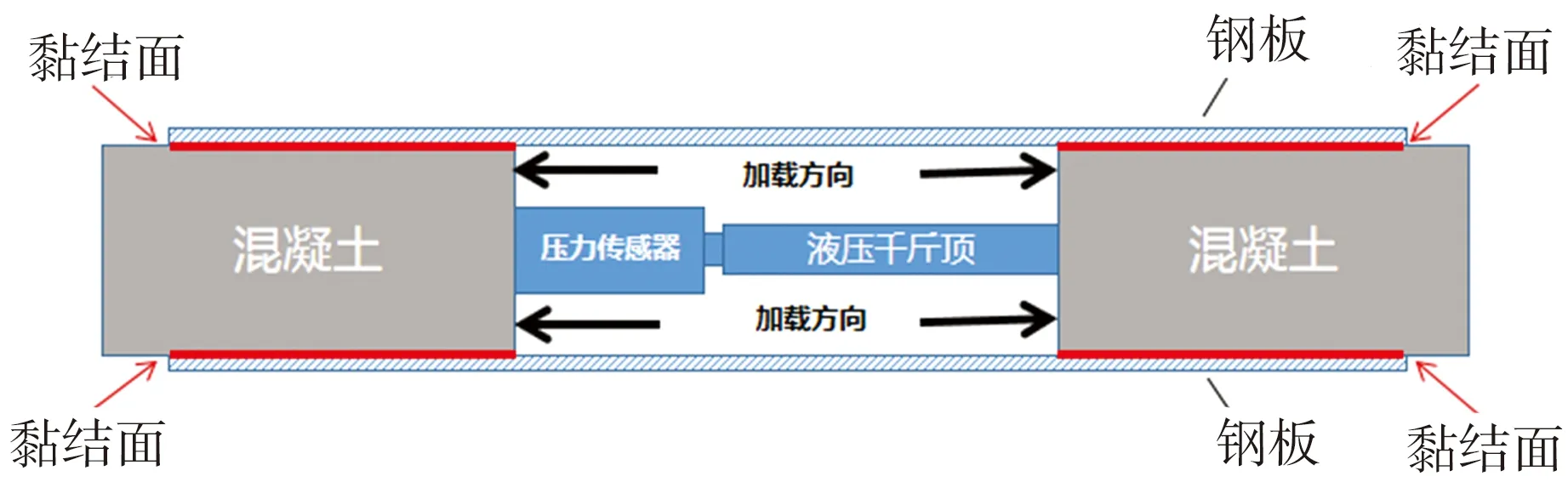
(a)试件加载装置示意图

(b)现场照片

Fig.1 Schematic diagram of specimen loading device and test site photo

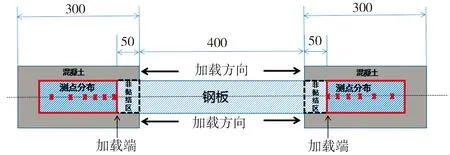
图2 测点布置方案(单位:mm)

2 试验结果

2.1 试件的破坏形式

经双剪切试验后，各组试件破坏情况及其破坏极限荷载见表4，部分试件遭破坏后发生完全剥离的黏结面照片如图3所示。从图3(a)可见，SJ1试件中发生完全剥离的黏结面表现为钢板与胶结层剥离破坏，钢板剥离后胶结层仍然完整地黏贴在混凝土表面上，而SJ4试件是因混凝土从内部剥离而形成完全剥离的黏结面(图3(b))，至于SJ5试件发生完全剥离的黏结面，胶结层与钢板、混凝土间均发生剥离，部分与混凝土剥离但仍黏贴钢板的胶结层上还残留一些被其带离的表层混凝土(图3(c))。分析所有试件的破坏形式表明，大部分试件主要发生了钢板与胶结层的剥离，并且破坏部位表现为脆性破坏，这应归因于钢板表面过于光滑，对钢板进行凿毛处理后再黏贴混凝土即可避免这种脆性破坏；同时，少部分试件还存在混凝土内部剥离破坏。

2.2 钢板表面应变分布分析

基于双剪切试验所测数据，获取各试件在不同荷载作用下其黏结面处钢板表面的应变分布情况。因为同一组试件的4个黏结面在发生剥离破坏前钢板表面应变分布趋势相似，故仅需考察试件发生完全剥离的黏结面，在此以胶结层中石英砂与结构胶体积比α分别为0.17、0.33的SJ2试件和SJ4试件为例进行分析，其中SJ2试件完全剥离黏结面上胶结层与钢板、混凝土间均发生剥离，而SJ4试件相应位置上则为胶结层与混凝土之间发生剥离，SJ2、SJ4试件黏结面处钢板应变分布曲线如图4所示。从图4(a)中可见，当荷载达到19.0 kN时，在SJ2试件钢板上距加载端25 mm处的应变值已超过距加载端5 mm处的相应值，表明该试件黏结面在此位置附近开始发生剥离；当荷载增至21.0 kN时，剥离位置转移到距加载端45 mm处；当荷载为24.0 kN时，黏结面已经剥离到距加载端75 mm处，而此时钢板加载端附近的应变也明显增大，这是因为钢板与胶结层几乎完全剥离，荷载主要由钢板承受所致；当荷载增至28.0 kN时，黏结面发生完全剥离破坏。对比不含石英砂的 SJ1试件(极限荷载为31.0 kN)，石英砂的少量掺入虽降低了SJ2试件中黏结面剥离的极限荷载，但同时也增大了钢板与胶结层之间的摩擦，有效延长了黏结面剥离的趋势，避免了黏结面在剥离开始初期就迅速发生完全剥离破坏。由图4(b)可知，SJ4试件黏结面在荷载为22.0 kN时开始发生剥离，此时钢板上距加载端25 mm处的应变值明显高于距加载端5 mm处的相应值，并且后者相较低荷载时急剧下降且为负值，此外，当荷载增大到24.0 kN时，钢板上距加载端45 mm处的应变也为负值，这可能是因为钢板本身有部分弯曲，弯曲部位与混凝土粘贴后存在初始应变，当黏结面发生剥离时该应变得到释放，从而导致钢板相关位置应变值突降为负值；随着荷载的不断增大，钢板上不同测点处的应变呈现阶段性突变趋势，表明试件黏结面沿着加载方向从加载端向自由端持续剥离。7组试件中，SJ4试件的极限荷载值最高，其黏结面的剥离形态为胶结层与混凝土间的剥离破坏且剥离持续过程较长，表明该试件胶结层掺入的石英砂含量适中，能明显增强钢板-混凝土界面的抗破坏能力。

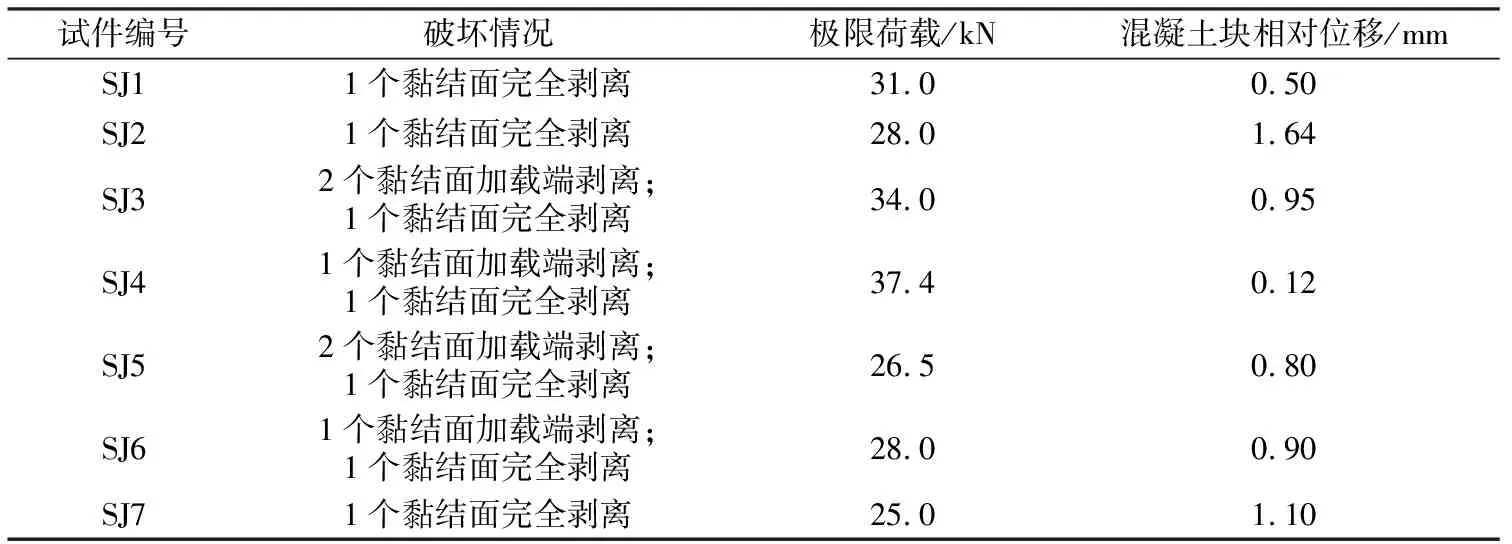
表4 试验结果

(a) SJ1 (b) SJ4

(c) SJ5

图3 部分试件破坏图

Fig.3 Failure of some specimens

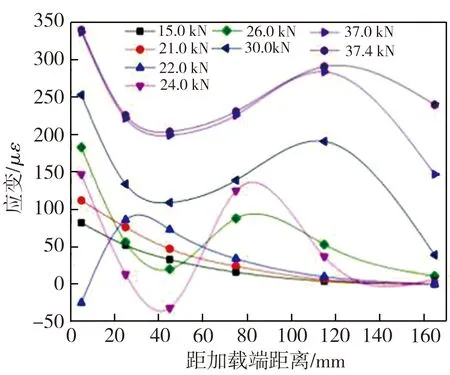
(b)SJ4

3 钢板-混凝土界面黏结滑移本构关系

3.1 剪应力与滑移量

在钢板-混凝土界面黏结滑移本构关系中，黏结界面上任意一点的剪应力及对应的滑移量是两个重要参数。基于差分法原理，剪应力与相应剪应变的关系式为

(1)

式中，τ为微段平均剪应力，MPa；tb为钢板的厚度，mm；dσ为微段应力差，MPa；dx为微段长度，mm；Eb为钢板的弹性模量，MPa；dε为微段应变差。假设钢板自由端处不产生滑移，则相应的局部滑移量表达式为

(2)

式中，s为测点所对应的滑移量，mm；xi为测点与自由端处水平距离，mm；εf表示测点与自由端之间任意位置的应变值。

3.2 界面黏结滑移曲线分析与模型修正

根据双剪切试验所测数据，利用公式(1)、(2)分别计算出在一定荷载作用下试件黏结面附近任意一点的剪应力及滑移量，进而绘制该点的黏结滑移曲线。以SJ4试件中加载端发生剥离的黏结面为例，该处钢板上靠近加载端附近的3个测点的黏结滑移曲线如图5所示。从图5中可以看出，3个测点的黏结滑移曲线具有类抛物线特征，在加载初期，测点剪应力随滑移量增大而近似线性增加；随着荷载的不断增大，这种增加趋势变缓直至剪应力达到最大值τmax，此时对应的滑移量为s0；当剪应力达到最大值τmax时黏结界面将出现损伤，之后剪应力开始下降而滑移量持续增大直至黏结界面发生剥离，此时滑移量达到极限值su。此外，通过比较3个测点的黏结滑移曲线可以看出，距离钢板加载端最近处(5 mm)测点的黏结滑移曲线能够更精确地反映整个加载过程中钢板-混凝土黏结界面的剥离过程，同时，该曲线与图6所示Nakaba模型[15]的黏结滑移曲线形式相似，且均以剪应力峰值τmax、剪应力峰值所对应的滑移量s0以及极限滑移量su作为界面黏结滑移关系的关键控制参数，因此可采用此处测量数据来分析相关界面的黏结滑移本构关系。

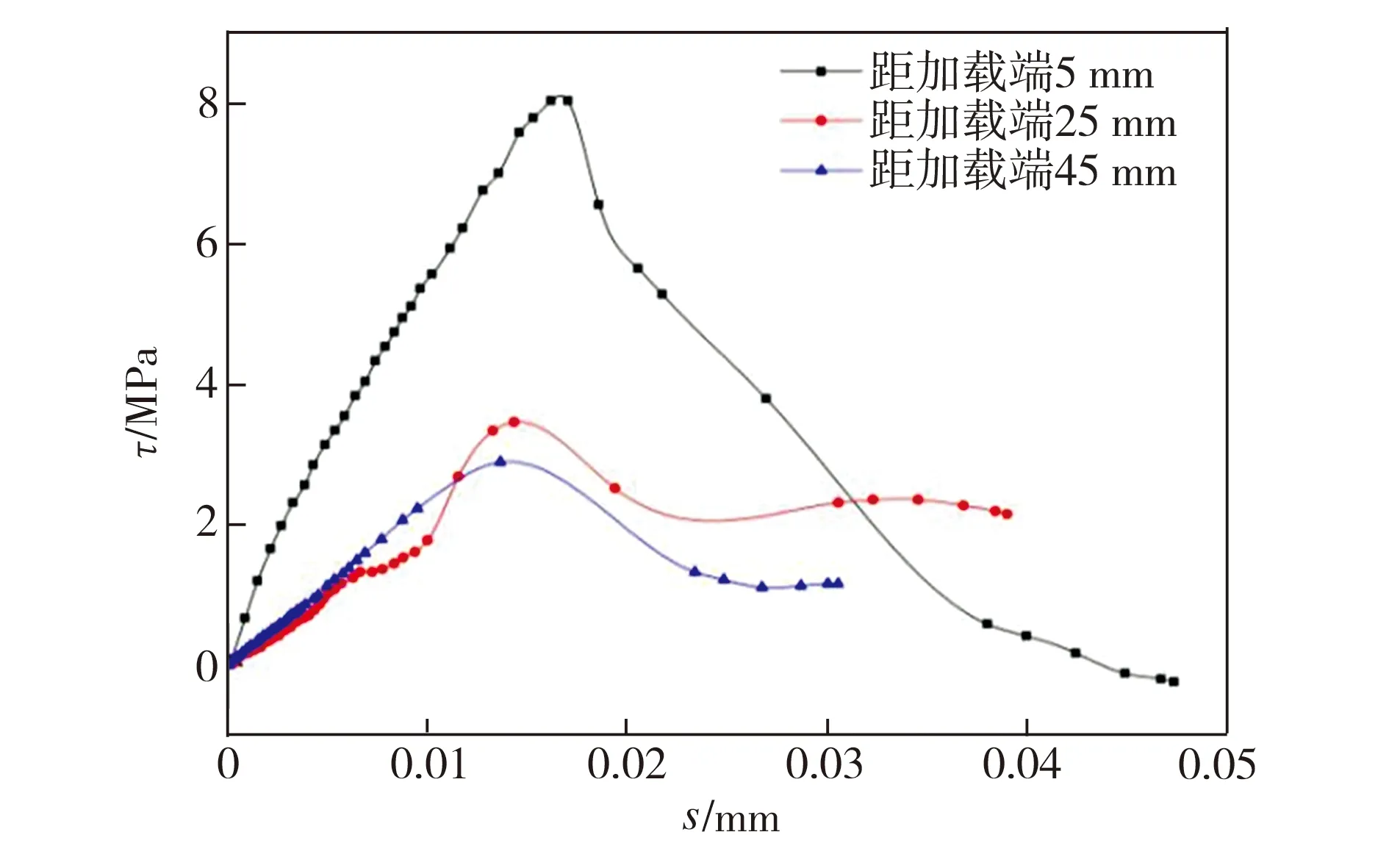
图5 SJ4试件的黏结滑移曲线

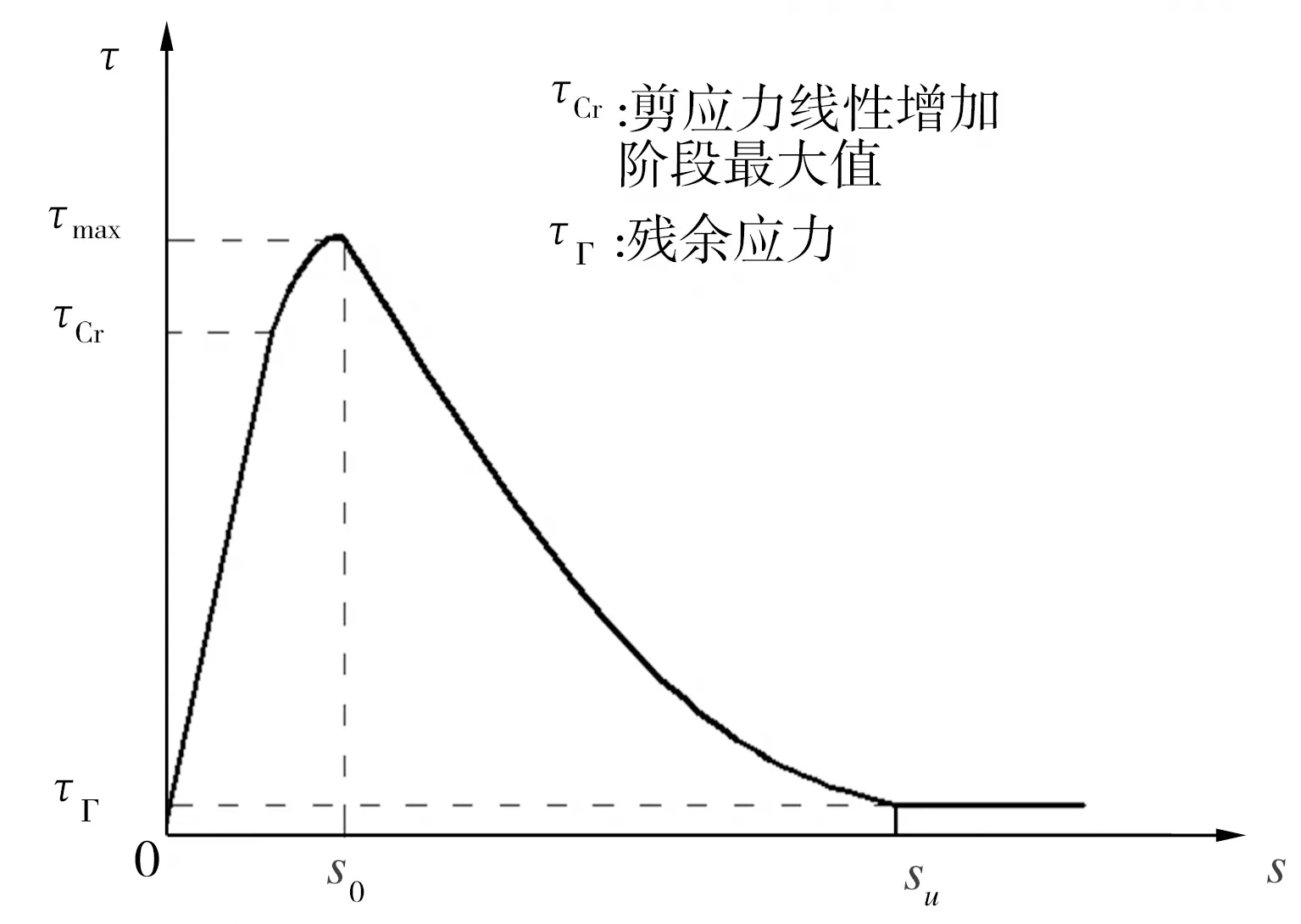
图6 Nakaba模型的黏结滑移曲线

为了使Nakaba黏结滑移模型更适合胶结层含石英砂的钢板-混凝土界面，利用试验数据对该模型参数进行检验和修正，Nakaba模型方程为

(3)

式中n为回归系数。在Nakaba模型中，τmax与混凝土抗拉强度有关，s0取为固定值，而在Neubauer模型[16]、Monti模型[17]及陆新征等提出的模型[18]中，τmax不仅与混凝土抗压强度有关，还与外贴板材、混凝土构件宽度比有关。再则，混合黏结胶层在混凝土层表面固化产生的化学胶结力以及二者之间的摩擦力都有助于增强界面黏结性能，而这些因素又受胶结层中石英砂含量影响，故修正模型时需综合考虑上述因素。另外需要指出的是，虽然7组试件大多为胶结层剥离破坏，黏结面极限承载力和极限滑移量su偏小，但试件加载前期的最大剪应力τmax及其对应的滑移量s0与之关系不大，所以不会对修正模型造成明显影响。对Nakaba模型进行修正的过程为：首先，由试件中钢板与混凝土块的宽度bp和bc求得宽度影响系数βw，计算公式为

(4)

其次，根据试件双剪切试验结果，结合Nakaba模型，在引入βw、混凝土抗拉强度ft、常数因子θ(θ值为1，mm·MPa-1)的基础上获得τmax、s0等黏结滑移参数与α的关系式

τmax=βwft(-740.01α5+1678α4-1365α3+

456.79α2-49.543α+1.9354)

(5)

s0=βwftθ(-3.2418α5+6.9731α4-5.3369α3+

1.6693α2-0.1678α+0.0049)

(6)

相应关系曲线如图7所示。由图7可见，在考虑βw、ft等因素后，随α的不断增加，τmax、s0均呈现出先减小再增大最后又减小的趋势。最后，获得胶结层含石英砂的钢板-混凝土界面黏结滑移修正模型：界面剪切力与相应滑移量的关系仍采用Nakaba模型(式(3))，但其中τmax、s0的计算方程

(a)τmax

(b) s0

Fig.7 Curves of relationship between bond-slip parameters andα

分别采用式(5)和式(6)，回归系数n取试验拟合平均值6.1005。

根据试验结果对修正模型进行验证，以胶结层中石英砂含量不同的SJ4、SJ5试件为例，其双剪切试验结果与相应的黏结滑移修正模型拟合曲线如图8所示。从图8中可以看出，在黏结界面切应力达到最大值以前的阶段，试验结果与修正模型吻合度较高；在界面切应力达到最大值后又开始下降的阶段，发生混凝土剥离破坏的SJ4试件试验值与修正模型依然吻合，但发生胶层剥离破坏的SJ5试件试验值与修正模型拟合度较差，不过二者整体变化趋势基本一致。总体来说，本研究在Nakaba模型基础上进行修正所得模型能较好地反映胶结层含石英砂的黏钢-混凝土界面黏结滑移本构关系。

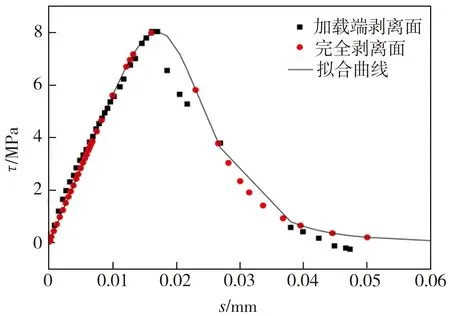
(a)SJ4试件

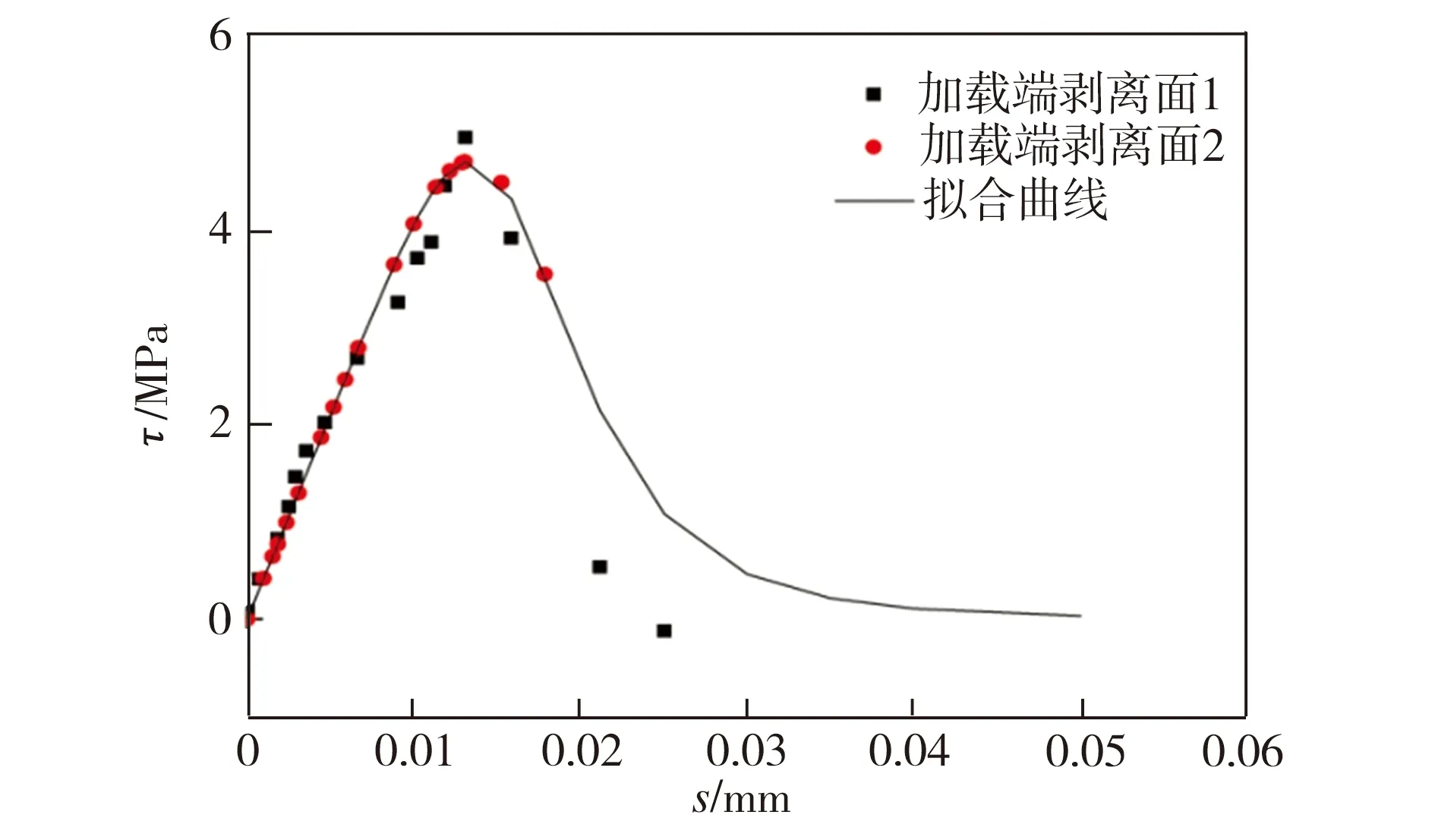
(b)SJ5试件

4 结语

本文设计了不同石英砂掺入量的黏钢加固混凝土结构件进行钢板-混凝土黏结界面双剪切试验，结果表明，在钢板黏结施工质量良好的前提下，钢板-混凝土界面的破坏形式主要为钢板与胶结层的剥离破坏，故实际工程中对钢板表面进行凿毛或锚固处理很有必要。当荷载较小未造成黏结面剥离时，随着与加载端距离的不断增加，钢板表面应变明显降低直至接近于零。当荷载较大造成黏结面发生剥离时，钢板表面应变峰值位置从加载端处沿加载方向往自由端转移，表明加载端处界面发生了剥离并导致附近区域应变下降，同时远离加载端处应变增大，这种剥离趋势逐渐向自由端发展。试件黏结滑移曲线主要由上升段与下降段组成，最大黏结剪应力τmax和其所对应的滑移量s0均随着胶结层中石英砂含量的增加而呈现出先减小后增大再减小的趋势，在本研究试验条件下，当石英砂与结构胶的体积比为1∶3时，黏结加固效果最好。考虑钢板、混凝土构件宽度比以及混凝土抗拉强度等因素，对Nakaba黏结滑移模型进行修正后所得模型与试验结果吻合度较高，更适用于胶结层含石英砂的钢板-混凝土界面黏结滑移本构关系分析。