谈初中数学教学中的变式教学
广西梧州岑溪市马路中学 广西 岑溪 543201
一、概念教学的变式
在概念教学中,变式教学是常用的方法.通过图形变式、语言变式、符号变式、公式变式等方面,使学生对概念的本质产生深刻认识。在马路中学185 数学课堂上,大致运用以下三种方式:
1、用直观的图形引入概念.
数学最初的概念都是基于直觉和学生已有的知识基础。例如:学习垂线的时候,我们可以借助于教室里的直观图形帮助学生理解什么是垂直,黑板,墙角的两条线之间的关系让学生从直观的图形中感受到垂线,建立起垂直的模型再抽象出它的特征,概括出它的定义。
2、类比的方法引入概念.
类比是根据两种或两类对象在某些方面的相似,得出它们在其他方面也有可能相似的结论。它是一种创造性的数学思想方法。如:类比一元一次方程得到一元一次不等式、二元一次方程、一元二次方程、一次函数等概念。在对比之下,既掌握了概念,又可以减少概念的混淆。
3、动手操作感受概念的形成.
在引入轴对称性质的时候,我们采取的就是动手操作方法,这样能够让学生留下深刻的印象,让学生准备几个方形纸片,让学生把它对折,在对折的纸片上用针刺一个三角开的图案再展开,让学生去观察,分析,归纳,探索先研究出对称点,再研究对称线段、对称三角形,这样就能更清楚地揭示轴对称的性质。通过上述的实验的演示、操作和讨论,使学生对轴对称的性质知其然又能知其所以然,让学生感受到学习的乐趣。这样学生容易理解也能留下深刻的印象。
二、例题教学的变式
1、已知条件不变,变换角度设计变式题,探索不同的结论.
例如:16 的算术平方根是_______________。
变式1:16 的平方根是_________。
变式3:已知a 的算术方根是2,则a=__________。
本题在条件不变下继续探索其它结论,使不同层次的学生得到不同得到发展,使学生经历获得通过猜想到验证的解决问题方法,培养学生探究能力与解决问题的能力。
2、改变或添加条件,从多个角度设计变式图探索结论。
例题:如图1,在平行四边形ABCD 中,E、F 分别是OB、OD 的中点,四边形AECF 是平行四边形吗?请说明理由。

图1
变式训练:变式1:若将例题中的已知条件E、F 分别是OB、OD的中点改为点E、F 三等分对角线BD,其它条件不变,问上述结论成立吗?为什么?
变式2:若将例题中的已知条件E、F 分别是OB、OD 的中点改为BE=DF,其它条件不变,结论成立吗?为什么?
变式3:若将例题中的已知条件E、F 分别是OB、OD 的中点改为E、F 为直线BD 上两点且BE=DF,结论成立吗?为什么?
一道题涉及到这么多的知识点,以及解决问题的方法和数学思想,让学生在熟悉的图形上发挥,扩大学生的知识面,使知识达到融会贯通。
三、思维方式方法的变式
1、一题多变.即改变题目的条件、改变结论、改变数据、改变图形、条件的引申或结论的拓展等等。把所学的各个方面的知识联系起来,加深对所学知识的理解,认识和体会到数学知识的整体性。在教学中应积极地引导学生从各种途径出发,用多种方法思考问题。
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b 的图象和反比例函数y=m/x 的图象的两个交点.求反比例函数和一次函数的解析式;

变式一、求直线AB 与X 轴的交点的坐标及△AOB 的面积;
变式二、求方程kx+b=m/x 的解(请直接写出答案);
变式三、求不等式kx+b-m/x<0 的解集(请直接写出案).
通过一题多变,让学生从不同角度思考问题、解决问题,可以引起学生强烈的求异欲望,培养学生思维的灵活性。
2、方法变式.一题多解,从多角度、多层次、全方位地去思考问题,找出一道题目的多种解决方法和途径,寻求最优化解决方案。
例如,如何复原一个被墨迹浸渍的等腰三角形?(只剩一个底角和一条底边)
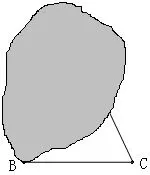
学生给出的三种“补出”方法:
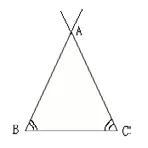
①量出∠C度数,画出∠B=∠C,∠B与∠C的边相交得到顶点A;
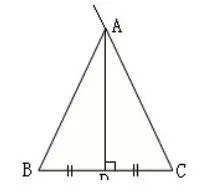
②作BC 边上的中垂线,与∠C 的一边相交得到顶点A;
③“对折”。
看画出的三角形是否为等腰三角形,由此引发全等三角形判定定理的证明。这道题从不同的角度进行多向思维,把三角形全等的知识点有机地联系起来,发展了学生的多向思维能力。
3、联想变式.
充分利用知识间的联系,将方程问题转化函数问题,将代数问题转化为几何图形问题,使学生举一反三、融会贯通。例如:在复习求一元二次方程:
x2-3x-4=0 的根时,可以进行以下变式:
变式1:你能结合二次函数图像求出x2-3x-4>0 的x 取值范围吗?
变式2:你能结合二次函数图像求出x2-3x-4 坐标轴的交点吗?
这样不仅培养了学生数形结合的思想,还开阔了学生的思维,进一步加深了对二次函数图像的认识和理解。
设计数学变式问题要内涵丰富,境界开阔,给学生留下足够的思维空间。因此,所选范例必须具有典型性。一要注意知识之间的横向联系;二要具有延伸性,可进行一题多变;三要注意思维的创造性和深刻性。在教学中,我们既要有强烈的变式意识,娴熟的变式方法,更要遵循变式教学的规律,合理安排变式教学的内容。如果我们能够把握变式教学和变式训练的正确方法和尺度,在数学教学中恰当使用变式教学和变式训练,希望帮助马路中学185 班全体学生从“题海战役”中解放出来,还对培养学生创造性思维,激发学生学习数学的兴趣,将起到比较积极的作用。相信同学们一定可以取得理想的学习效果。
变式教学是中国基础教育中的精华,值得我们去传承;变式教学是一种十分重要的教学思想,值得我们去钻研;变式教学是经实践证明的有效教学模式,值得我们去实践。

