“梯形的面积”探究性学习的实践与思考

长沙市雨花区砂子塘新世界小学

《新课程标准（2011 版）》指出：“数学知识的教学，应注重学生对所学知识的理解，体会数学知识之间的关联”。同时新课标也指出：“不同的人在数学上得到不同的发展。”“梯形的面积”的学习是建立在平行四边形和三角形面积计算的基础之上，梯形面积计算公式的探究和应用，学生自然会想到把梯形转化为学过的图形来研究，具体怎样转化？是割补？还是拼摆？是转化为平行四边形?还是转化为三角形？都可以让学生自主探索。教学中我设计了用“等拼法”求梯形内部的平行线段的和；用“等拼法”求梯形的面积；用“倒着算”求梯形的高等，用“等差数列的和”求梯形的面积；又用梯形的面积公式探究“高斯求和定理”。使教学方法和教学指导同步进行，注重对学生探究能力的培养，体现“方法比知识重要”的价值观，实现学习的“再创造”，提升学生学习的综合素质。

[探究一]有些梯形问题往往不能直接解决。可以根据题意用“等拼法”完成。即取两个或多个与所求图形完全相同的图形拼起来，构成一个整体，然后利用所求图形与这个整体之间的关系进行求解。

[题目］：如图1，梯形ABCD 中，AB＝1O 厘米，CD＝2O 厘米，斜边AD 被等分成5 等份，过各分点引AB 的平行线相交于斜边BC。求梯形内部4 条线段的总长是多少厘米？

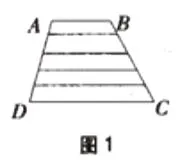
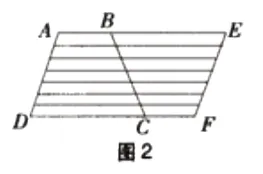
［探究与解析］取与梯形ABCD 完全相同的梯形CFEB，将这两个同样的梯形拼成平行四边形AEFD，如图2，梯形ABCD 与梯形CFEB 内部的4 条线段对应相等，并且被拼成4 条长度等于：1O＋2O＝3O（厘米）的线段，所以梯形ABCD 内部4 条线段的总长是30×4÷2＝60（厘米）。

[探究二]在不知道梯形上底、下底和高的条件下，知道它们之间的一些间接条件，灵活运用梯形的面积和“等拼法”方法求梯形的面积。

[题目］：梯形的上底乘高是36 平方厘米，梯形的下底乘高是56 平方厘米，求梯形的面积是多少平方厘米？

［探究与解析］：（1）梯形的面积公式s=（a+b）×h÷2 变形得：s=（ah+bh）÷2=（36+56）÷2=46（平方厘米）（2）由题意可知：36 和56 的最大公约数是4 也就是梯形的高，那么梯形的上底就是9 厘米，梯形的下底就是14 厘米。梯形的面积s=（a+b）×h÷2=（9+14）×4÷2=46（平方厘米）（3）如图：用“等拼法”将梯形面积变成一个大长方形与一个小长方形面积的差的一半再加上小长方形面积来求。

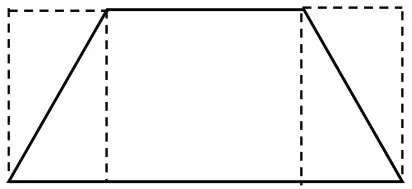
梯形的面积s=（56—36）÷2+36=46（平方厘米）

探究这类问题各种方法的时候，不必马上让学生统一到梯形的面积计算的规则公式中来，那样有套用模式之嫌。可以让学生观察、思考，把各种方法进行沟通，理解，统一。

[探究三]在梯形的有关学习中，有时遇到求梯形的高、下底或上底是多少的问题，引导学生探究梯形的面积公式的特点，灵活进行变形，用“倒着算”来解决会迎韧而解。

[题目]梯形的面积为120 平方厘米，高为20 厘米，上底为3 厘米，下底为多少厘米？

［探究与解析］：用画图帮助学生理解、解决这道题后，还可以采用“倒着算”来解决。根据（上底+下底）×高÷2=梯形的面积，倒着来从答案出发，除以2 变成乘2，乘高变成除以高，加上底变成减上底，就变成了梯形的面积×2÷高—上底=下底。同样道理，也可以用“倒着算”来求梯形的高和上底，也可以求三角形的底和高。这样，学生利用倒着算的知识可以很容易地记住梯形的上底、下底、高怎么求，三角形的底和高怎么求。

[探究四]五年级有许多学生都学过等差数列，可以把梯形的面积计算公式和等差数列结合起来：求梯形的面积可以通过把梯形中长的底剪掉，并到短的底中，使上下底相等，就是移多补少的数学思想，再求出梯形的面积。求等差数列的和，也是把大的数移给小的数，使每个数的大小相等，再求和，也是利用了移多补少的数学思想，所以，我们可以把求等差数列的和看成求梯形的面积，也可以把求梯形的面积看成求等差数列的和。

[题目]一堆钢管，最上层3 根，最下层15 根，每一层比上一层多一根，13 层。这堆钢管一共有几根？

［探究与解析］：这堆钢管的截面就是一个梯形，这道题我们可以利用梯形的面积计算公式，把上层3 根看成上底，下层15 根看成下底，13 层看成高，一共有几根钢管看成求面积。就是（上层根数+下层根数）×层数÷2 即（3+15）×13÷2=117（根）。其实这一题也可以看成是一个等差数列：3+4+5+……+15，这样，就可以变成等差数列公式：（首项+末项）×项数÷2=等差数列的和，即（3+15）×13÷2=117（根）。数学知识之间存在着一定的关联，梯形面积的计算与看似毫不相干的“倒着算”，“等差数列的和”竟有如此密切的联系。让学生在探究知识的同时感受类比和转化的思想，提高分析问题和解决问题的能力。

[探究五]在上述第四个问题中，进一步深入探究，“梯形的面积看成求等差数列的和”中的“求等差数列的和”是不是和著名的“高斯求和定理”有联系呢？数学家高斯就是从小就爱动脑筋，爱问为什么的孩子。他10 岁那年，数学教师布特纳要求学生求出1 到100 这一百个自然数的和。不一会儿，高斯就把算出了准确答案的石板交给了老师。在这之前，老师从未教过学生计算等差数列方面的知识，这就是著名的“高斯问题”。

［探究与解析］：如果我们今天也来解答那个著名的“高斯问题”：1＋2＋3……＋98＋99＋100＝？大家不会真的把一百个自然数连续相加求和的办法。可以用高斯的方法解决：求1 至100 这一百个自然数的和，采取头尾两数相加的办法：1＋100、2＋99、3＋98、4＋97……这样能得到50 个101，用101×50 便能迅速地求出它们的和是5050。当然还有其它的解法，如果我们用凑整百数的办法：1＋99、2＋98、3＋97、4＋96……便能得到49 个100，再用100×49的积加上中间的数50 与最后的数100，也能求出这一百个自然数的和。如果我们再展开想象的翅膀，把这一百个连续的自然数视为一个梯形，它的上底是1，下底是100，高是100。根据求梯形面积的公式：S＝（a＋b）×h÷2，这一百个自然数的和＝（1＋100）×100÷2＝5050。这个算法太奇妙了！假若数学家高斯还活在世上的话，他一定会坚起大拇指说：“中国的小学生真棒！”

学生在自主探究的学习过程中不一定都是一帆风顺的，方法也各异，有猜疑、矛盾、困惑、也有惊喜。但学生独立探究的过程，不单单获得了新的数学知识，更学会了科学的研究方法，增强了克服困难的信心，获得了成功的喜悦。作为数学教师自身要加强专业知识的学习，才能引导学生更好的进行自主探究的学习，并对数学知识进行融会贯通。