基于模型预测控制算法的轻型长航程AUV航控系统研究
黄 琰 ,胡 峰 ,俞建成 *,乔佳楠 ,王振宇,谢宗伯
(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;2.中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110016;3.中国科学院大学,北京 100049)
自主式水下航行器(Autonomous Underwater Vehicle,AUV)作为目前主要的海洋自主移动平台已经获得广泛的应用[1-3],而有限的续航能力是影响AUV技术在海洋观测领域中拓展应用的主要制约因素之一。区别于常规AUV,面向海洋时变中小尺度过程长期精细观测需求而研制的轻型长航程AUV具备类似于水下滑翔机的浮力调节和重心调节机构[4-5],使得这种AUV在定深直航过程中可以根据海水密度自适应调节载体净浮力和航行姿态,具备长时间高效巡航能力,大幅提升了AUV的巡航范围。
目前,国内外在浮力可变的AUV的航行控制算法领域研究较少。美国Tethys长航程AUV利用PID深度控制方法,采用并行PID外环读取深度误差和深度变化率,并产生俯仰和浮力命令,控制内部浮力调节机构、水平舵调节机构和质量块调节机构3种执行器[6-7];张勋等[8]在设计了AUV均衡系统的基础上,构建了深度控制、纵倾控制和浮态控制模型,并基于PID和均衡系统设计了深度控制、纵倾控制和浮态控制方法;姜志斌等[9]针对具备均衡系统的定点观测型AUV设计了基于级联控制和跟踪微分器的AUV下潜控制方法。上述研究在AUV技术实现时均采用PID控制或分段PID进行航行运动控制,当在海洋环境突然发生变化(如海水密度减小)时,采用基于PID的控制算法调整浮力和重心可能造成俯仰角震荡、浮力超调等问题,使得执行机构在产生多余不必要的能耗的同时,系统无法得到令人满意的动态响应,进而也影响了AUV续航指标的提升。
采用模型预测控制算法可以很好地解决AUV系统时滞而产生的动态响应和轨迹跟踪等问题。Geng等[10]将带执行机构约束条件的模型预测控制应用于AUV的深度控制中,并在试验中表现出较好的控制性能。杜亮等[11]研究了近水面航行的AUV模型预测控制方法,该方法提高了AUV在波浪干扰下的系统动态响应。本文针对轻型长航程AUV实现零攻角高效定深航行的要求,开展轻型长航程AUV航行控制技术研究。在轻型长航程AUV系统组成及其航行控制系统设计基础上,基于模型预测算法设计了AUV深度控制器。最后,通过仿真验证了控制算法的有效性。
1 轻型长航程AUV的系统组成
本文讨论的轻型长航程AUV采用模块化设计思想,兼顾系统的功能性、可靠性和可扩展性,分为艏部传感器舱段、能源舱段、姿态调节舯段、浮力调节和航向控制舱段和推进舱段5个舱段。AUV载体外观如图1所示,内部关键机构布置结构如图2所示。

图1 轻型长航程AUV载体外观图

图2 轻型长航程AUV内部机构布置示意图
AUV的艏部舱段主要安装避碰声呐、多普勒测速仪(DVL)、温盐深传感器(CTD)以及其他科学载荷;能源舱段主要安装有固定电池组和浮力调节装置;姿态调节舱段安装有重心调节装置、包括电子罗盘在内的航行控制系统、通信系统以及应急抛载装置等;航向控制舱段安装有垂直舵组件和水平舵组件;推进舱段安装有2叶低速螺旋桨推进装置。
经系统优化设计,轻型长航程AUV在空气中自重约200 kg,最大航行速度2 kn,最大不间断巡航距离可达2 000 km。
2 AUV航行控制系统设计
AUV的航行控制系统由航行控制器、执行机构、状态观测器以及各传感器构成,控制系统的结构如图3所示。
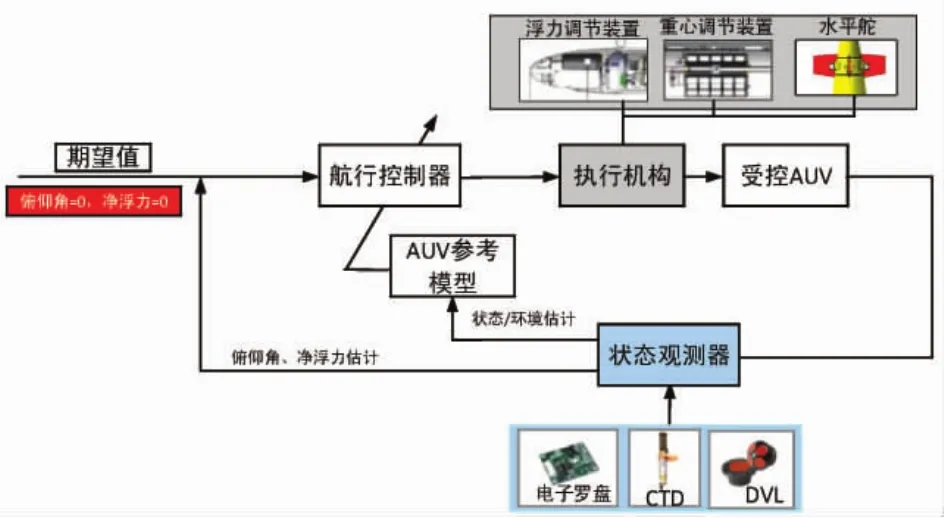
图3 AUV的航行控制系统的组成示意图
在航行过程中,系统通过获取电子罗盘的三轴姿态数据、温盐深传感器(CTD)换算获得的海水密度和深度数据、以及多普勒测速仪(DVL)的三向速度数据,估计AUV的航行状态和环境参数。通过状态估计和航行目标期望值相比较,计算AUV的航行状态偏差,并通过控制器算法输出控制量给各执行机构。在本研究中,执行机构主要包括浮力平衡机构、重心调节机构和水平舵。
AUV在水下长时间大范围巡航时,可能会跨越多个不同密度的水团,而不同海水密度的变化会带来浮力的改变,常规AUV不得不通过调整航行姿态以克服浮力变化的影响,导致自身航行效率降低。轻型长航程AUV由于其浮力量和重心位置的可调性,可以通过浮力和重心调节始终保持零攻角的航行状态,最大限度地减少海洋环境变化带来的航行效率损失。
另一方面,由于轻型长航程AUV的重心调节和浮力调节成为AUV航行控制的新增输入量,控制输入量间的非线性耦合无法被忽略,直接通过PID等传统控制方法无法得到令人满意的系统动态响应,因此需采用模型预测控制算法实现AUV的高效定深航行性能。
3 模型预测控制器设计
3.1 深度控制目标转化
轻型长航程AUV不具备侧向推进能力,只能采用水平舵、重心调节机构控制俯仰角进行航行深度的调节,具有一定的欠驱动特性。采用简化视线导航法(Line-of-Sight,LOS)[12]将 AUV 垂直面深度控制转化成俯仰角控制问题,如图4所示。图中,H0为目标深度线,当前AUV质心Pt(ht)距目标深度线的垂直距离(航迹偏差)为ek,且ek需要收敛到0。以当前位置点作一个半径为R的圆(R足够大),则所作的圆与目标深度线的交点中位于AUV前方的交点定为当前视线导引点Plos,进而可求出当前目标俯仰角为:

式中:Θlos为目标俯仰角;Θmax为AUV允许的最大俯仰角。

图4 AUV深度控制视线导航法示意图
由于AUV航行深度的变化是通过俯仰角的改变实现的,而在使AUV产生俯仰力矩的同时,必然会在垂直载体轴线方向上产生一个与AUV目标深度变化方向相反的垂向速度。如图5所示,当AUV目标深度线位于载体下方时,需要使AUV保持向下的俯仰角。此时,AUV具有载体轴向方向上的速度u以及垂直载体向上的垂向速度w,两者在深度方向上投影的差值使AUV趋向目标深度线运动,且w的影响在大部分时间可以忽略不计。但是当AUV接近目标深度线时,其目标俯仰角θ较小。当usinθ=wcosθ时,深度方向上的绝对速度分量为0,AUV会保持当前的俯仰状态向前航行,即不能达到目标深度又不能保持零攻角高效航行状态。为解决这一问题,在长航程AUV深度控制中,引入俯仰角修正项,对目标俯仰角进行修正。当θ较小时,sinθ=θ,cosθ=1,因此目标俯仰角修正项可以表示为:

则修正后的长航程AUV深度控制目标俯仰角为:


图5 AUV速度分解示意图
3.2 面向控制的垂直面系统建模
3.2.1 浮力和重心可调的AUV垂直面动力学建模参考潜艇标准六自由度运动方程以及平面运动假设[13],并考虑AUV浮力和重心调节机构对剩余浮力和重心的改变,得到轻型长航程AUV在垂直面内的动力学模型为:
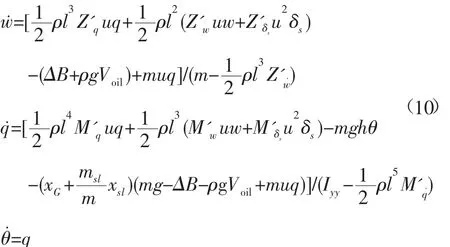
式中:m为AUV质量;ρ为环境海水密度;l为AUV艇长;g为重力加速度;xG为AUV重心坐标;h为 AUV 稳心高;u,w,q为 AUV 速度;u˙,w˙,q˙为 AUV加速度;θ为AUV俯仰角;ΔB为AUV剩余浮力;δs为水平舵舵角;Iyy为AUV绕y轴转动惯量;Voil为排油量(向外油囊排油为正);msl为滑块质量;xsl为滑块移动位移(向艏部移动为正);Z'q˙,M'q˙等为 AUV所受的无因次化水动力系数项。
由式(10)可知,由于在系统模型中重心调节和浮力控制量存在耦合,同时控制会造成系统的动态响应较差。因此,为了设计符合AUV航行需求的模型预测控制器,首先需建立两个独立的状态空间方程来实现系统的解耦。即在实际AUV巡航过程中,采用浮力调节机构和重心调节机构分时执行的策略,水平舵始终参与控制保证AUV的航行姿态稳定。
3.2.2 浮力调节过程的AUV状态空间方程 轻型长航程AUV浮力调节机构工作时,AUV剩余浮力状态的改变会导致系统状态方程产生偏差。为了反映出浮力调节对系统状态的影响,以及便于后续设计观测器对剩余浮力进行辨识,对系统状态变量进行扩展,加入剩余浮力ΔB项。将x=(w,q,θ,ΔB)T代入式(10)并重新整理,得到:

将其在时间域上进行离散,得到扩展后的轻型长航程AUV空间状态方程:
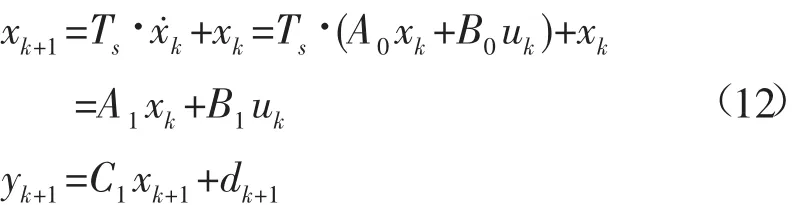
式中:x=(w,q,θ,ΔB)T表示系统状态矢量;u=(δS,Voil)T表示控制输入量为水平舵舵角和浮力油囊调节量;yk=(Θ,ΔB)T为系统输出;Ts为采样时间;A1,B1,C1分别表示维数为 4×4,4×2 和 2×4 的状态系数矩阵;dk为系统扰动。
3.2.3 重心调节过程的AUV状态空间方程 将AUV重心坐标xG扩展加入到系统状态变量中。将x=(w,q,θ,xG)T代入到AUV状态方程中,并在时间域上进行离散,得到扩展后的基于水平舵和重心调节的状态空间方程:
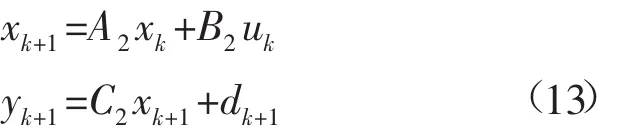
式中:x=(w,q,θ,xG)T表示系统状态矢量;u=(δS,xslide)rT表示控制输入量为水平舵舵角和浮仰滑块调节量;yk=(Θ,ω)T为系统输出;A2,B2,C2分别表示维数为4×4,4×2和2×4的状态系数矩阵。
3.3 双模型切换的模型预测定深控制器设计
在AUV长期水下定深直航过程中,浮力调节过程的AUV状态空间方程(3.2.2节所述)和重心调节过程的AUV状态空间方程(3.2.3节所述)的建立基于双模型切换的模型预测定深航行控制器,实现AUV在海洋环境变化(如密度变化、上升流等)时的快速调整响应。基于双模型切换的模型预测定深航行控制器主要由模型切换规划器、浮力调节模型预测控制器、重心调节模型预测控制器3部分组成,如图6所示。
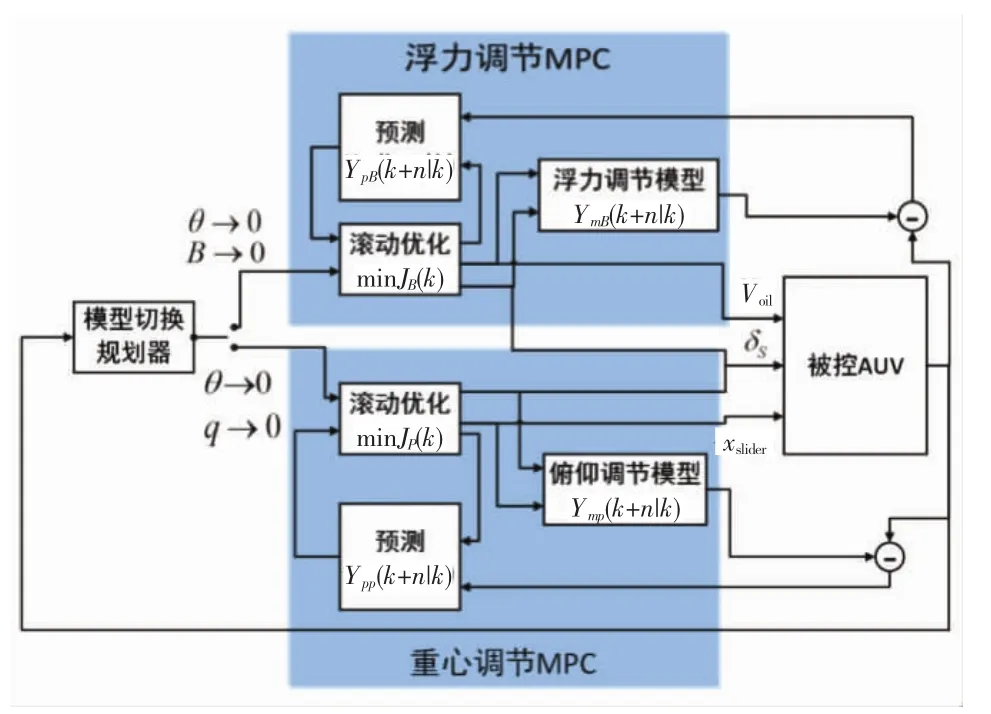
图6 AUV双模型切换定深控制器
由式(12)和式(13)可知,AUV 基于浮力调节过程的空间状态方程和基于重心调节过程的空间状态方程具有相同的表现形式:

因此,可以统一描述两种模型预测控制器的设计过程。将状态方程(14)进行迭代、整理即可得到系统的输出预测方程为:

其中:yk+n|k表示在k时刻预测k+n时刻的系统输出值;xk表示当前状态量;uk-1表示前一步输入控制量;Δuk+n|k表示预测k+n时刻控制输入增量;Hu表示控制时域;Hp表示预测时域。
考虑AUV控制过程中的控制量极限约束和控制增量约束[14]。控制量约束和控制量增量约束的表达形式为:

由于在控制时域内需要求解的是控制量的增量,因此约束条件中也只能以控制增量形式出现,需要对控制量约束式(16)进行转换:

式中:Umin和Umax分别表示根据控制量约束计算得到的控制量增量上下限。
为保证AUV能够快速平稳地追踪期望轨迹,目标函数需要加入系统输出量的偏差和控制量的优化。同时,为解决有约束条件下可能出现的无法得到最优解的情况,有必要在目标函数中加入松弛因子[15]。目标函数如下:
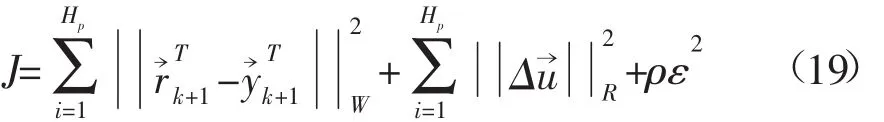
式中:r→k+1表示目标轨迹;W和R分别表示输出量权重系数和控制量增量权重系数;ρ为权重系数;ε为松弛因子。
综合目标函数和约束条件,基于空间状态方程的预测控制器在每个控制周期内要解决如下的优化问题:
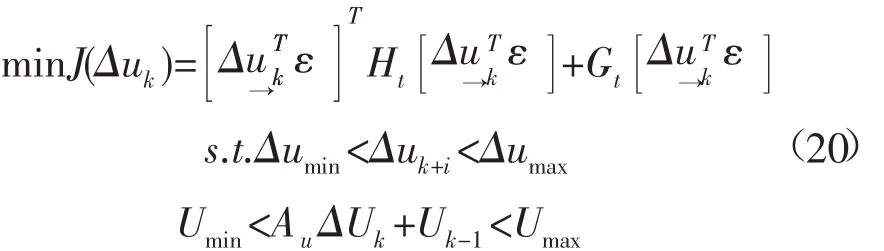
式中:
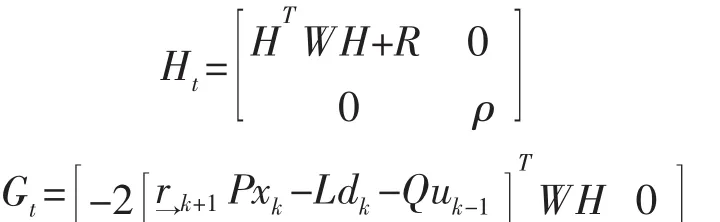
采用内点法[16]进行最优控制量的计算。在每个控制周期内完成上述优化问题的求解后,得到控制时域内的一系列控制输入增量和松弛因子:

将该控制序列中第一个元素作为实际控制输入增量作用于系统,即:

进入下一个控制周期后,重复上述过程,如此循环实现对AUV期望轨迹的控制。
4 仿真试验与分析
通过仿真对AUV深度控制策略进行验证。假设AUV在水中10 m深处进行定深航行,航速为0.5 m/s。AUV水平水平舵舵角最大为±20 deg,最大转动速度4 deg/s;浮力调节最大排油量为±0.2 L,最大排油速度为0.04 L/s;滑块最大移动量为±0.1 m,最大移动速度0.02 m/s。同时假设AUV在1 000 s时由于外界环境因素(海水密度)的变化导致自身浮力值减少1.5 N,并通过3.3节设计的双模型切换MPC控制AUV定深航行。仿真结果如图7~图9所示。

图7 AUV深度和俯仰角输出曲线

图8 AUV输入控制量曲线
由仿真结果曲线可知,初始时AUV在水下10 m处进行零攻角定深航行。在1 000 s时,由于AUV自身浮力的改变,导致AUV偏离预定航行轨迹,触发系统观测器辨识出自身剩余浮力差值。假设在1 250 s时,系统启动水平舵加浮力调节控制器对浮力进行调节,对AUV轨迹进行修正,并在1 400 s处使AUV重新进入无剩余浮力稳定运行状态(历时150 s)。可以发现,此时AUV定深航行的深度有偏差(9.8 m),航行纵倾角也不能保持零攻角状态(-2 deg)。为了使自身恢复零攻角直航状态,在1 500 s时AUV切换为水平舵加重心调节控制器,进行纵倾角和轨迹的修正,在1 800 s时各机构调节完成(历时300 s),最后AUV在惯性作用下于2 000 s处恢复零攻角定深直航(10 m,0 deg)。仿真结果表明,通过水平舵加浮力调节控制器和水平舵加重心调节控制器的联合控制,可以均衡AUV自身浮力变化对AUV航行性能的影响,实现AUV高效的定深航行能力。同时,系统输出曲线较为光滑,执行机构的调节频率较低,基本上无超调现象。两种控制器进行深度控制时均具有良好的姿态保持和定深性能。
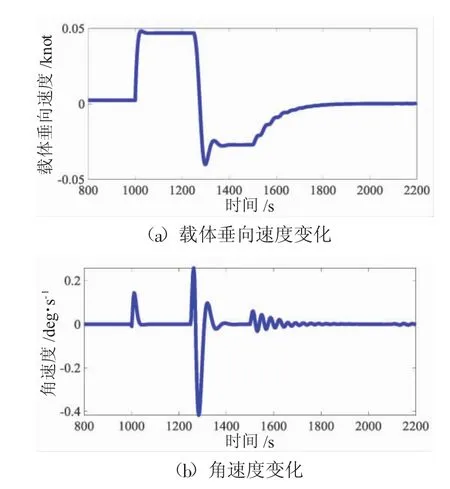
图9 AUV垂向速度和俯仰角速度曲线
5 结论
与常规AUV主要依靠水平舵或垂直槽道桨抵消净浮力进行定深航行的方式不同,轻型长航程AUV具备了浮力调节和重心调节能力,可实现中性零攻角的长时间高效定深航行。针对新的控制输入量带来的控制耦合问题,文中设计了一种基于双模型切换的模型预测深度控制器,通过分别建立基于浮力调节和基于重心调节的扩展空间状态方程,实现了对浮力和重心控制输入量在控制模型上的解耦。通过仿真验证,基于模型切换的模型预测深度控制器能够有效对AUV浮力变化进行均衡响应和姿态调整,使AUV恢复零攻角直航状态。控制过程中浮力、俯仰和水平舵的调节频率较低,可以有效降低执行机构的磨损以及能量的消耗。该控制器设计方法对其他可变浮力的长航程AUV控制器设计具有参考借鉴作用。

