抛锚贯入深度计算方法比较研究

冯士伦 ，朱晓宇 ，李 焱*，唐友刚 ，赵志娟

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350；2.天津大学 天津市港口与海洋工程重点实验室，天津 300350；3.天津大学 建筑工程学院，天津 300350）

随着世界经济的发展，我国的航运业得到了充分的发展，商船进行抛锚作业的频次大幅增加，同时，海底输油管道等海底设施也不断增多，商船抛锚引发海底管线事故时有发生。锚贯入海底过程中恰好击中海底油气管道等海底设施，可能导致海底管道发生泄露或设施损伤，从而对原油输送和油田作业带来巨大损失。为避免船舶抛锚造成海底管道等海底设施的破坏，通常的做法是将海底管线或海底设施埋入土中一定深度。因此，船舶抛锚后贯入海底土深度计算，便成为了决定海底管线等海底设施埋设深度的关键因素。

陈峰等[1]基于能量法计算了黏土与砂土土质下大抓力锚的贯入深度，并进行了现场试验，证实了能量法可以较好地拟合试验的实测落深，揭示了船锚的质量和下落高度对锚的贯入深度的影响规律。庄元等[2]提出了一种较为简单的物理模型，分析并预测了船锚在海底土中的贯入深度。李晓松等[3]分析了船舶抛锚时锚的运动全程的受力，建立了船锚触底速度的求解模型，而后使用微分方程法计算了锚最终的贯入深度。雷震名等[4]将能量法与正交试验法结合，研究了海底管道对不同的影响因素的敏感性，得出了管道的最小推荐设计埋深。李庆等[5]采用DNV的相关方法，计算船锚在下落过程中的有效冲击能量和落锚的最终贯穿深度，并用微分方程法计算了抛锚-拖锚-停滞的最终深度，为穿越航道的海底管道的保护提供了一定的理论指导。

Y H Kim等[6]对鱼雷锚的动态贯入深度进行了深入研究，研究表明：锚的贯入深度是冲击速度、剪切强度对应变率的依赖性、剪切过程中的重塑程度以及土壤敏感性的函数。Wenkai Wang等[7]在实验室用9种不同的鱼雷锚进行了128组试验，根据能量守恒原理和试验测量结果，提出了不考虑土壤分离工况下锚杆贯入深度的计算公式。结果表明，能量法计算的侵彻深度与实验室和现场实测的侵彻深度吻合较好。Haixiao Liu等[8]通过研究粘土和砂土的参数，研究了承载力系数、粘滞系数、不排水抗剪强度、内摩擦角、侧土压力系数等因素的影响，推导了在粘土与砂土中计算锚极限埋深的公式，结果表明，在给定合适的参数值的情况下，可以合理地预测粘性土中锚杆的极限承载力。其中，参数的选择是影响计算精度的最重要的因素。

船舶抛锚贯入海底的深度的影响因素十分复杂，已知的主要有锚型、锚重、触底速度、海底土物理特性等。目前，世界上各个国家对锚贯入深度的计算方法尚未形成统一的认识，还没有明确提出贯入深度的通用计算公式。现有的船锚贯入深度研究方法主要有基于DNV规范的能量法与基于牛顿第二定律的微分方程法。锚的触底速度大小直接影响锚贯入海底时的冲击能量，它也是公式法计算时的重要影响因素。因此，无论哪种计算方法，触底速度的精确计算都十分有必要。本文以不同重量的霍尔锚为例，基于CFD方法计算抛锚下落过程的速度及触底速度，使用正交试验原理分析船锚贯入深度对不同影响因素的敏感性，为海底管线等海底设施的埋设深度提供依据。

1 抛锚贯入深度计算方法

目前计算抛锚贯入深度使用较多的是DNV规范中的能量法与利用牛顿第二定律推导出的微分方程法。

1.1 能量法

DNV-RP-F107给出了采用能量法计算船锚的落深的方法[9]，认为船锚的冲击能量完全被土体吸收，基于能量守恒原理，土体对船锚所做的功等于船锚在下落过程中的冲击总能量，由此可以计算出船锚的贯入深度。

锚对海底土的冲击能量，与结构自身质量和附连水质量有关，包括附连水在内锚体的冲击总能量为：

式中：EE为锚触底时的冲击总能量，kJ；Ep为锚触底时的动能，kJ；EA为附加水动力能量，kJ；m为锚的质量，kg；ρw为海水的密度，kg/m3；V为附加水的体积，m3；Ca为附加质量系数，该值取决于物体的几何形状，根据工程经验，本次研究中对于掉落的锚取Ca=1.5。

海底土质吸收船锚的冲击能量，可以用式（2）计算[6]：

式中：Ek为海底土质吸收的能量，kJ；h为船锚贯入深度，m；γ'为土的有效单位重量，kN/m3；Sr为锚的形状系数，与锚冠水平投影面积有关，依据规范要求，霍尔锚的形状系数取值为0.6，其余锚的形状系数可同样参考该规范取值；Nr为与内摩擦角有关的土承载力系数。根据API RP 2GEO规范中的推荐方法，如下式所示：

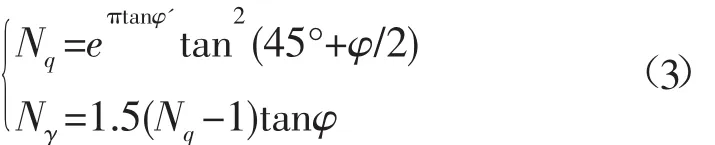
式中：φ 为土的内摩擦角，(°)；Nq与Nγ为 φ 的无量纲函数，Nq=(exp[πtanφ＇])(tan2(45°+φ/2))；Nγ=1.5(Nq-1)tanφ

1.2 微分方程法

锚在贯入海底土质的运动过程中会受到重力、土端阻力、土摩擦阻力、拖曳力等的作用，从而使锚做减速运动并最终停止。贯入深度的影响因素很多，以下方程式主要反映了锚的触底速度、锚型、锚重、海底土特性等的影响。

锚贯入海底土的运动可以使用牛顿第二定律表示：

式中：M*为锚在土中的有效质量，kg；W为锚的水下重，等于锚的重力减去浮力，N；y为锚在土中的贯入深度，m；FBP为土底部承载力，N；FAD为土侧向承载力，N；FH为拖曳力，N。具体计算见式（5）～式（10）：

式中：Su为土的不排水抗剪强度，N/m2；Nc为土极限承载力系数；Nγ，Nq为土承载力系数，与上节中相同；δ为土的侧向承载力系数；St为黏土的灵敏度；AF为锚的前端面面积，m2；As为锚的侧面面积，m2；CD为拖曳力系数；ν为锚的速度，m/s；P0为深度为y的有效覆压，N/m2；γ为土在水下的单位重量，N/m3；C为锚面短边的长度，m；α为土和锚之间的摩擦角，（°）；q0为平均有效覆压，N/m2；Kp为被动土压力系数；φ为土的内摩擦角，（°）。

本文开发了计算机程序，基于微分法计算锚体下落过程的轨迹和贯入深度。当锚的速度减小到0时，对应锚贯入海底的最终深度。

2 参数选择

2.1 海底土质参数

当船锚接触到海底土以后，会对海底土产生一个竖直向下的作用力，由于相互作用力的影响，海底土很容易出现变形，并给船锚一个向上的反作用力。在该力的作用下，船锚会不断减速，直到速度减为0。贯入深度与海底土质密切相关，海底土一般有淤泥、石子、黏土、砂土等，因此需对分析海底土质的参数对于贯入深度的影响。本文以3种典型黏土与1种典型砂土为例，分别计算船锚的贯入深度，其主要物理参数如表1所示。

表1 海底土的主要物理性质参数

根据文献[10]，黏土的侧向承载力系数取值为0.23～0.40，本文取为 0.40。粘土的灵敏度[11]St：一般介于1.5～5，计算中取St=3；无量纲Nc为土的极限承载系数[12]，在锚贯入计算中取为9.0。

2.2 锚参数

使用以上两种方法计算船锚贯入量的过程中，除了锚的触底速度ν，锚的质量M、锚的水平投影面积Af和侧投影面积As同样是非常重要的参数。

霍尔锚是商船抛锚常用的锚型，小型、中型、大型商船抛锚需要分别使用相对应重量的霍尔锚。以下计算分别选取重量为2 t，5 t，8 t和10 t的霍尔锚，同时使用其对应的投影面积。

当计算锚的投影面积时，参照富志禹等[13]提出的船用锚水平投影面积估算公式，计算得到霍尔锚在不同锚重下锚冠水平投影面积，使用2016年发布的国标《霍尔锚》（GB/T 546-2016）中霍尔锚的数据，计算锚的侧投影面积。

表2 霍尔锚锚冠投影面积

根据DNV-RP F107规范规定，物体从球形到更复杂形式的拖曳阻力系数范围为0.6～2.0。根据文献[14]，霍尔锚的拖曳力系数Cd取1.0时，其极限速度偏小，受到的阻力偏大。本文保守假定霍尔锚的拖曳力系数Cd=0.7。

3 贯入深度计算

3.1 抛锚触底速度分析

船舶抛锚时，将锚从锚链孔处释放，直至锚接触海底土的过程中，锚分别经历了锚穴-水面、水面到泥线两个不同的运动过程，触底速度与锚在空气中运动和水中运动过程有关。忽略锚链的作用，锚在空气中运动时仅受重力作用；锚在水中运动时受重力、水阻力的作用。

采用ICEM软件对霍尔锚进行建模和流场、网格划分，编写锚自由下落的UDF文件，导入FLUENT软件中，利用CFD原理对锚下落20 m以及25 m后的下落速度进行计算。使用ICEM软件建立的简化模型如图1所示。计算取15 m×15 m×40 m的矩形流体域，并进行动网格划分，如图2所示。

流域顶部设置为压力出口，四周设置为对称边界，以模拟无限范围的流域。使用VOF方法模拟液体和空气的两相流动，采用动网格中的自动更新网格方法控制结构下落时的网格质量，使用PISO方法进行数值离散，初始时刻，设置抛锚的位置处于水面以上5 m。计算时间步长取0.002 s，总计算时间为8 s。

图1 霍尔锚的简化模型

图2 计算域及网格划分

根据上一节的计算设置，得到结构下落8 s后的速度历程和距离历程，从而得到结构在水中运动20 m以及25 m处的下落速度，纵坐标0点为水面，水面以上设为正值，如图3所示。

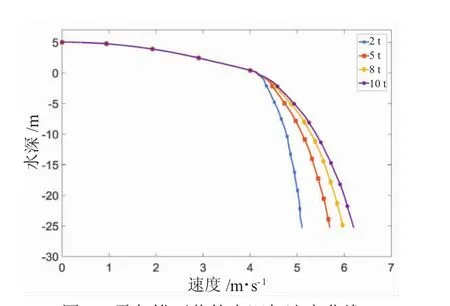
图3 霍尔锚下落的水深与速度曲线

从图3中可以得到如下结论：（1）霍尔锚在水中运动20 m和25 m后，触底速度主要集中在5～7 m/s之间；（2）触底速度随水深的增大而增大；（3）结合文献[15]中公式4.9,霍尔锚投影面积增加的速度小于质量增加的速度，因此，触底速度随锚质量的增大而增大。

3.2 锚贯入深度分析

3.2.1 能量法 分别选取锚重为 2 t，5 t，8 t，10 t的霍尔锚，根据计算得到的触底速度，计算霍尔锚下落过程中具有的冲击总能量，如表3所示。

表3 不同锚重抛锚触底速度与冲击总能量

针对4种不同土质，使用能量法的式（1）～式（2），开展船锚贯入深度计算，分别得到不同锚重的霍尔锚在水中下落20 m与25 m的相关计算结果，如图4～图5所示。

由图4～图5可见，不同土质对应的霍尔锚贯入深度由大到小依次为淤泥、软黏土、一般黏土、砂土，这表明霍尔锚贯入海底土的深度与土质有关，随土质的变化而发生变化。同时，不同锚重下的贯入深度不同，10 t重的霍尔锚在水中下落25 m后贯入淤泥的深度最大，为3.89 m；2 t重的霍尔锚在水中下落20 m后贯入砂土的深度最小，为0.86 m，这表明霍尔锚贯入海底土的深度与锚重有关，随锚重的变化而发生变化。

3.2.2 微分方程法 针对黏土和砂土这两种海底土质，基于式（4）～式（10）使用微分方程法，开展船锚贯入深度计算，分别得到不同锚重下霍尔锚在水中下落20 m与25 m的相关计算结果，如图6所示。

由图6可知，霍尔锚贯入海底土的深度受锚重、海底土质、水深等的共同影响。霍尔锚贯入海底土的深度随锚重的增加而增大；霍尔锚贯入黏土层的深度明显比砂土层更大；水深增大，霍尔锚的贯入深度也随之增大，但是对黏土层的影响比砂土层更大。

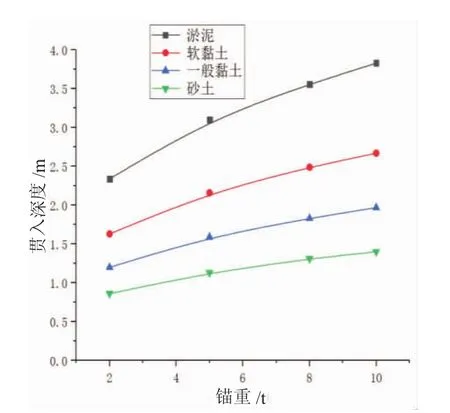
图4 霍尔锚下落20 m的贯入深度

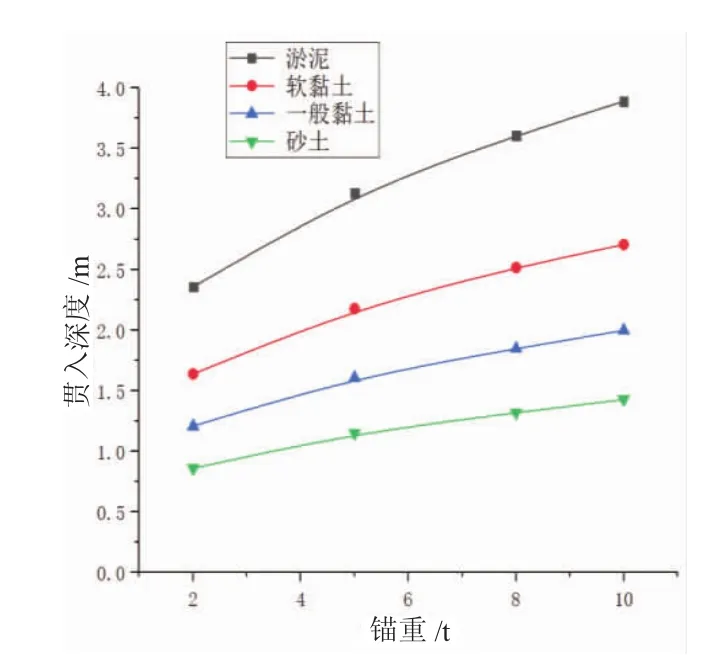
图5 霍尔锚下落25 m的贯入深度

图6 霍尔锚不同锚重的贯入深度

4 正交试验分析

抛锚贯入深度明显受到多个因素的控制和影响。通过正交试验分析，对两种计算方法进行参数敏感性分析，明确两种方法影响因素的主次顺序，这可为实际工程计算提供指导。

4.1 能量法

使用能量法计算抛锚贯入深度过程中，锚重、触底速度、土的有效重度、内摩擦角是其主要影响因素。根据文献[16],黏土的有效重度最大约为17 kN/m3，砂土的内摩擦角最大为35°，因此下面取合理有效重度范围、合理内摩擦角范围的黏土为例，将这些影响因素作为正交试验的试验因子，计算出实验所需参数，将其用于下面的正交表中，如表4所示。

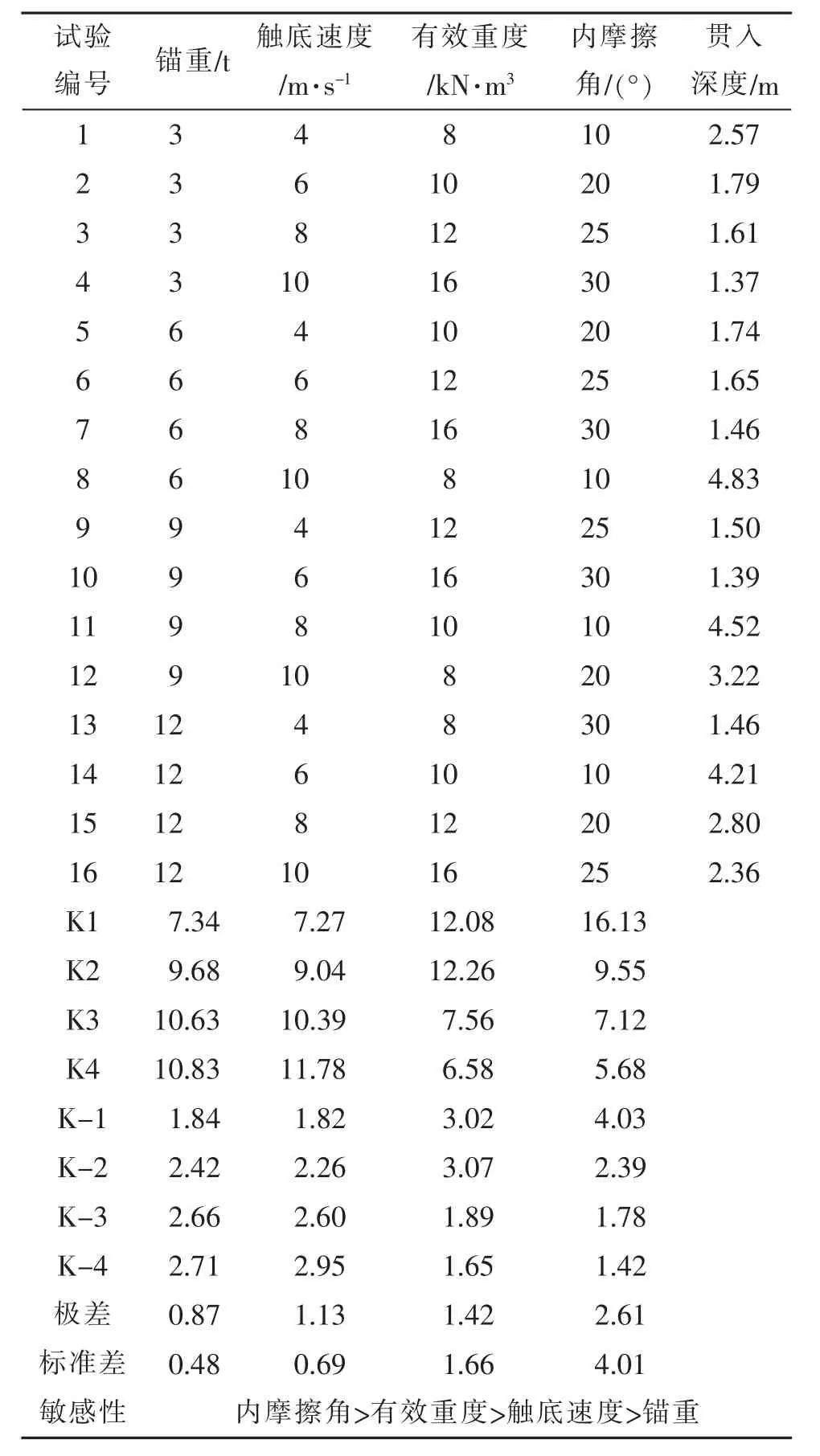
表4 正交试验表

由表4可知，最大极差值为2.61，最小极差值为0.87，分别对应内摩擦角和锚重，这表明对于贯入深度影响最大的因素为内摩擦角。从表4中标准差也可以得到相同的结论。

4.2 微分方程法

对微分方程法进行综合分析研究，可知，使用微分方程法计算贯入深度过程中，需要将海底底质分为黏土和砂土两种不同底质状况。底质为黏土时，锚重、触底速度、土的有效重度、不排水抗剪强度是影响贯入深度的主要因素；底质为砂土时，锚重、触底速度、土的有效重度、内摩擦角是其主要影响因素。下面以海底底质为黏土时为例，计算出实验所需参数，将其用于下面的正交表中，如表5所示。

表5 正交试验表

由表5可知，最大极差值为1.39，最小极差值为1.16，分别对应有效重度和锚重，这表明对于贯入深度影响最大的因素为有效重度。从表5中标准差也可以得到相同的结论。

5 结论

本文采用能量法与微分方程法计算了船舶抛锚贯入海底土的深度，得到如下结论：

（1）文中采用能量法计算出的贯入深度值总体来看比微分方程法要大，这是因为使用能量法计算没有考虑能量耗散，所以计算结果较大。

（2）使用能量法与微分方程法计算出的结果曲线变化趋势一致，表明两种计算结果都具有合理性，能量法计算的贯入深度较大，以此为基准铺设海底管线较为安全。

（3）通过正交试验可知，两种计算方法均遵循以下规律：随着土的有效重度增大，锚受到的阻力增大，其贯入海底的深度随之减小；土的内摩擦角增大，土体之间的摩擦力增大，土更加难以贯入其中，因此锚贯入海底的深度随之减小。

（4）船舶抛锚贯入海底的深度大小受到锚的重量、锚的触底速度、土的有效重度、土的内摩擦角、土的不排水抗剪强度等因素的影响，使用能量法计算过程中，参数敏感性依次为：内摩擦角＞有效重度＞触底速度＞锚重；使用微分方程法计算过程中，参数敏感性依次为：土的有效重度＞触底速度＞不排水抗剪强度＞锚重。

（5）使用微分方程法计算过程中，最大极差值1.39与最小极差值1.16相差0.23，差距不大，说明敏感性差距不大。

因此，对于使用能量法计算贯入深度时，内摩擦角的选取尽量合理准确；而在使用微分方程法计算贯入深度时，4个主要影响参数均应尽量合理选取，全面考虑。