基于IRI的卫星高度计电离层Keras神经网络模型研究

薛文文，苗洪利，苗翔鹰

（中国海洋大学 信息科学与工程学院，山东 青岛 266100）

电离层对微波的延迟是影响微波遥感对地面及海洋观测的重要因素。特别是对于卫星高度计对海表面高度的厘米级测量精度，电离层延迟会带来较大的测高误差。电离层延迟主要取决于电离层中的电子密度及总电子含量（Total Electron Content，TEC）。国际参考电离层（International Reference Ionosphere，IRI）构建了分层模型，用以预报平静电离层的平均状态，能够准确预测80%以上的微波路径上的电子含量[1-2]。但是，IRI模型构造复杂、参数较多，不利于模型的推广使用[3]。近年来，国外学者通过IRI与高度计实测数据进行分析，认为IRI表示在电离层变化情况上具有较高的精确度。但是，用户一般在其官网上通过输入必要的时间、位置及高度参量而获取总电子含量[4]，为在单频卫星高度计上应用该模型带来困难。基于大数据的深度学习可以通过网站获取大量数据，建立基于IRI的神经网络模型[5]。

Keras是基于Tensorflow后端，由Python语言编写的一种高层神经网络结构。Tensorflow是Google的开源框架，是当今大数据、人工智能、图像识别及深度学习等领域的强大工具。Keras由于具备高效可扩展的序贯模型和函数式模型，其性能优于传统BP算法。

本文基于IRI电离层预测值，通过Keras网络框架构建一个神经网络模型，利用Jason-2卫星高度计双频法测得的总电子含量值对神经网络模型进行检验，旨在将该模型应用于单频高度计的电离层延迟校正。

1 数据及方法

1.1 IRI-2016模型数据获取

IRI官网（http://irimodel.org/）给出 IRI-2016 在线运行界面，可以输入时间及位置等信息获取所需电离层电子含量。但是这种交互式操作，对于几十万甚至上千万的数据量来说难以操作。本文采用Python编写程序，通过程序获取所需数据原理示意图如图1所示。

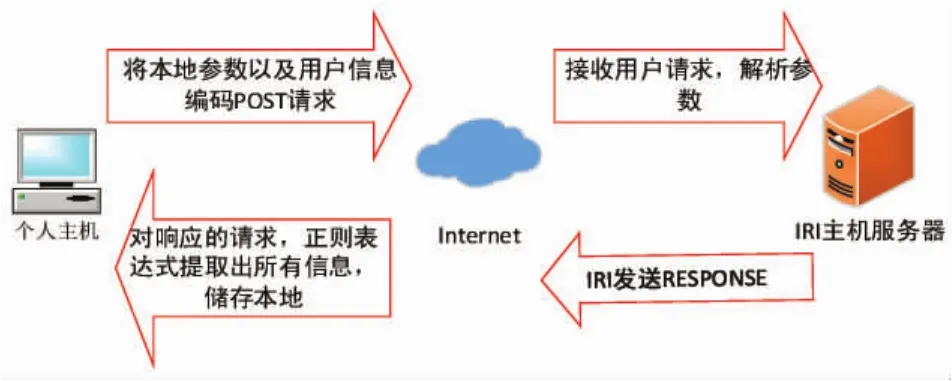
图1 IRI数据获取原理图

在客户端将所需要的请求数据进行POST编码后发送请求到服务器，服务器会根据POST请求发送response响应给客户端。客户端收到服务器发来的数据后，使用Python解析库将需要的信息提取并且保存在本地计算机。本文使用的爬虫信息与IRI官网上信息一致，包括时间信息（year，month，day，time），位置信息（latitude，longitude，height），还有可选信息F10.7 radio flux（10.7 cm的太阳辐射通量是太阳活动的极好指标[6]。它通常被称为F10.7指数，是太阳活动中运行时间最长的记录之一）等，这样得到的总电子含量TEC，记为TECIRI[7]。

1.2 Jason-2轨道匹配及数据提取

选 取 Jason-2的 GDR（Geophysical Data Records）中2016年Cycle281数据，每个Cycle由近10 d、254个 Pas（s升降轨）、127圈构成。

提取其中Ku波段的时间、经度、纬度及对应的用双频法测得的电离层延迟值Δ，Δ与总电子含量TEC的关系如式（1）[8-9]所示:

根据式（1）可以算出总电子含量：

f为Ku波段的频率，其值为13.575 GHz；总电子含量TEC的单位为TECU，1 TECU=1016el/m2。

1.3 IRI-2016与Jason-2观测电子含量对比

在Jason-2的Cycle281中提取Pass11-Pass30(10圈，接近1 d)的时间、经纬度、高度及Ku波段电离层延迟等信息，利用式（2）将电离层延迟换算为TEC值，记为TECJason-2。

对比Jason-2与IRI-2016的TEC值，必须首先进行时间和空间信息的匹配。将Jason-2数据中的时间，经度、纬度、高度信息依次输入到网络获取软件的POST请求当中，这样就可以得到时间和位置完全匹配的两列TEC数据。按时间排序的两列TEC数值分布见图2所示。

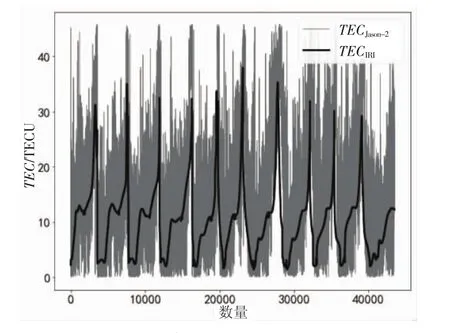
图2 电离层总电子含量分布

从图2可以看出，Jason-2绕地球每一圈，其观测到的与地面之间的总电子总量具有周期性，反映了地面固定位置电离层分布的日周期性，而IRI-2016模型值表现出与Jason-2观测值较强的分布一致性。

Jason-2利用双频观测法进行每秒一次的实时观测，受实时环境因素影响，会产生较大波动，而IRI-2016模型值是由多层公式积分而得，其结果必为连续可微函数值，其分布为平滑曲线。

由于IRI-2016模型值与双频法测量值分布及量值基本一致，因此，基于IRI-2016模型值深度学习的Keras神经网络模型可以用于卫星高度计的电离层延迟校正。

2 Keras神经网络模型的建立

深度学习的数据集来自IRI-2016模型中2016年将近300万组数据，经纬度的精度为0.01°，时间的精度为36 s。70%用于训练模型，30%用于测试模型。深度学习对计算机性能要求极大，本文选取IRI模型适当的时间及空间精度，同时兼顾学习时间和模型结果准确率[10]。

Keras神经网络模型的时间输入分为两个部分：一部分为年积日，即从每年的1月1日起开始累计的天数，另一部分为日积时，即每天的时刻数（以0.01小时单位）。同时输入的参数还有空间位置信息，包括经度（longitude）、纬度（latitude）、高度（height）及 F10.7信息。

图3为Keras神经网络模型结构示意图，将前述输入参量作为输入层，选择合适的激活函数以及模型的优化器将各层数据输入训练。模型的层数以及各层的节点数需要不断地训练调整，直到损失达到最小及梯度不再下降，进而固定各层参数，完成模型的建立。

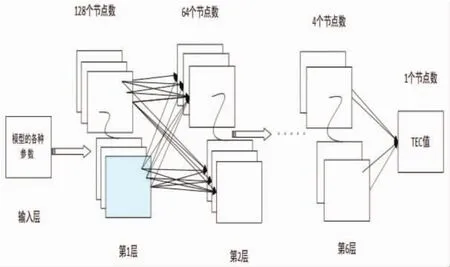
图3 Keras神经网络模型结构

本文全链接采用6层网络，前5层的激活函数均为“relu”，最后一层采用“linear”。在隐含层选用“relu”是因为它具有如下优点：克服梯度消失的问题与加快训练速度。最后选用“linear”线性激活函数，为了补偿网络输出结果的线性偏置[11]。

对所建立的Keras网络模型，只要将待测日期和时间分解为年积日和日积时，连同待测位置的经纬度及高度输入模型，即可输出总电子含量TEC值，记为TECKeras。当然，本文所建模型固定高度为Jason-2的轨道高度（1 336 km），模型只针对于特定的高度计[9-10]。

3 模型测试

神经网络模型的建立均需要测试，一般采用数据集的20%用于模型测试[12]。图4为模型输出值TECKeras和数据集中的目标值TECIRI的拟合散点图。

图4 TECKeras和TECIRI拟合散点图

由图4可以看出，Keras模型输出值与IRI-2016的模型值具有很好的一致性。统计结果表明，二者的均方根误差为0.72 TECU，相关系数高达0.99。这说明Keras模型具有较高的有效性和可靠性。

4 模型应用与结果分析

将所建模型应用到Jason-2的Cycle281-290中的数据，从结果中选用两个PASS做出细节描述。图5为Pass17和pass18一圈的TEC分布。

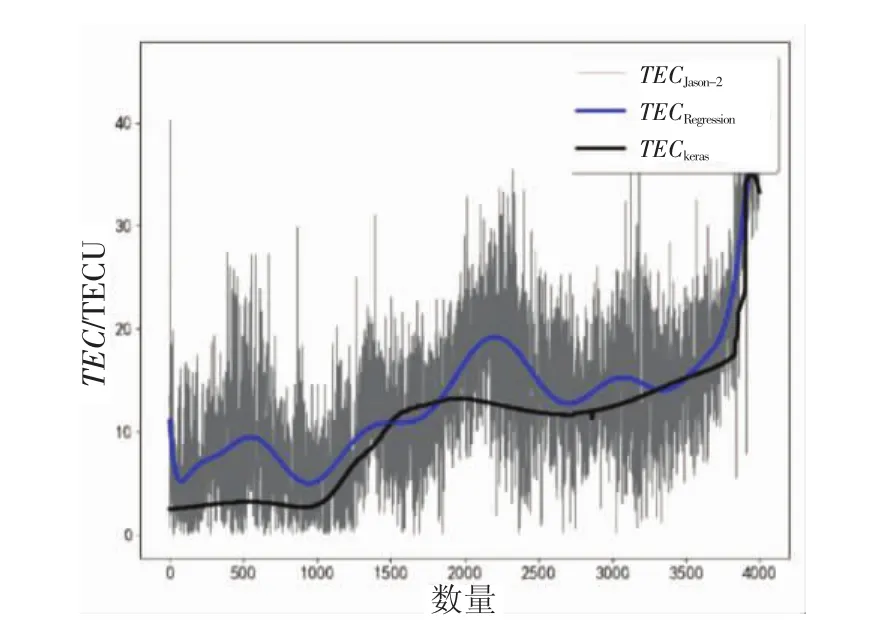
图5 单圈双频观测值和Keras模型值分布

图中，灰色线为Jason-2双频测量的TEC值，为了与Keras模型值（黑色线）进行有效对比，将其进行多项式拟合，其拟合线见图5中的蓝色线。从中可以看出，拟合后的TEC值分布整体与Keras模型值分布较为接近。但是也可以看出，在部分地区Jason-2的测量值与网络模型输出值存在偏差。图6为单圈情况下两者的误差分布直方图。

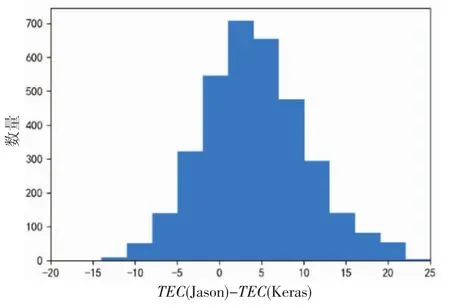
图6 Jason-2与模型输出值TEC误差分布直方图

如图6所示，Jason-2与模型值两者的偏差一般在-15～20 TECU之间，且分布集中区域为-5～10之间，这样的误差分布表现出两者的一个系统性偏差，大约为 4～5 TECU。

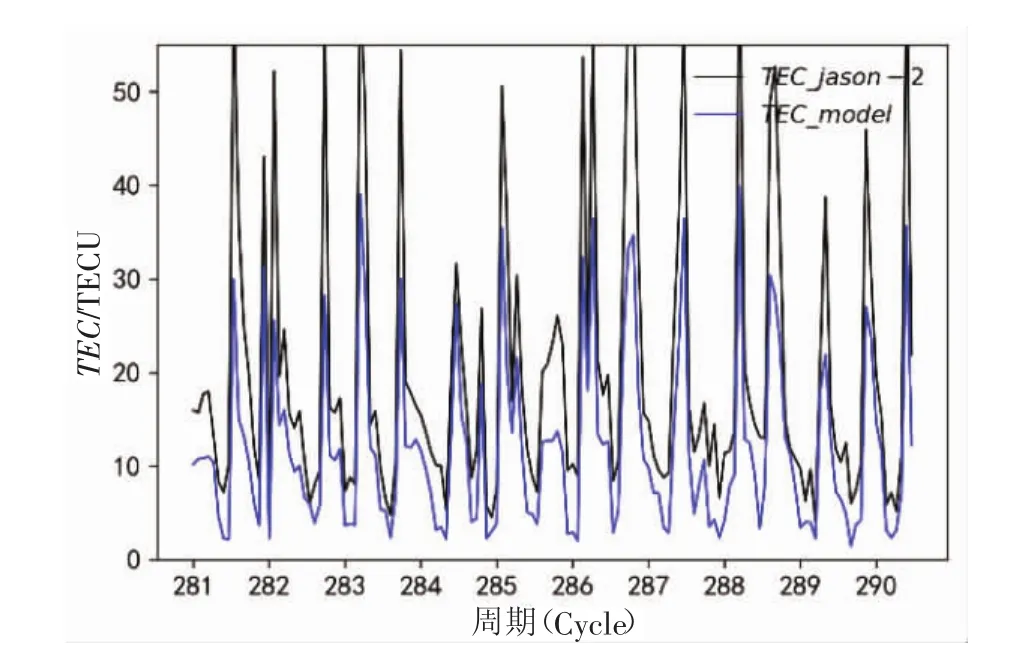
图7 Jason-2与Keras模型值对比

如图7所示，选用Cycle281-290的高度计数据，TECJason-2为双频观测数据，TECmodel为Keras模型输出数据，模型输出值在各Cycle的Jason-2数据上表现出良好的一致性，对于范围更广的测量区域做出两者的数据分布图[13]。统计10个Cycle的各自均方根差（RMSE）和相关系数及平均值，结果见表1所示。

从表1可以看出，二者在各个Cycle内的均方根误差比较稳定，均值为4.46 TECU，换算为Ku波段的电离层延迟为8.5 mm，对于测高精度为厘米的卫星高度计有良好的提升，毫米的电离层延迟误差可以接受[14-15]。二者的相关系数均值为0.75，此结果为原始双频观测数据与模型对比得到，而原始双频观测数据相邻点存在测量误差，其值波动较大，如图5所示，如果进行平滑处理，会提升其相关系数。尽管两者的相对误差达到0.25左右，但是TEC值当TECU达到较大值30 TECU时候，两者的误差也就为6 TECU左右，符合之前对模型的误差分析。从图7得到，在模型推广到其他Cycle的时候，模型输出值精度和各Cycle数据相同，具有较高的准确率。

表1 Jason-2双频观测值与Keras模型值对比

5 总结

本文采用python编程在IRI网站获取了与Jason-2卫星高度计Cycle281-290同轨道信息的IRI-2016模型电离层总电子含量数据。通过将该数据与Jason-2利用双频法测得的总电子含量比较，二者均具有明显一致性。

基于IRI-2016数据，通过深度学习建立了Keras神经网络模型。经测试，模型输出值与测试数据集中的目标值之间的相关系数高达0.99，均方根误差为0.72 TECU，说明模型有效。

将所建Keras神经网络模型应用于Jason-2卫星高度计，对比模型值与双频观测值。结果表明，二者在10个cycle的平均电子含量均方根误差为4.46 TECU，平均相关系数为0.75，对应的Ku波段传输延迟值为8.5 mm。

本文所建立的Keras神经网络模型只适用于Jason-2及与其同轨道高度的高度计，这是由于建模时选用Jason-2的轨道高度。IRI模型是从电离层以不同高度分层的数据获得的经验模型，只要选取不同轨道高度的IRI数据建模，就可将模型应用于任意高度单频高度计的电离层延迟误差校正。