合成孔径雷达高度计与传统高度计精度比对分析与机载试验验证

刘 鹏 许 可 王 磊 史灵卫 于秀芬



合成孔径雷达高度计与传统高度计精度比对分析与机载试验验证

刘 鹏①②③许 可*①②王 磊①②史灵卫①②于秀芬①②

①(中国科学院微波遥感技术重点实验室 北京 100190)②(中国科学院国家空间科学中心 北京 100190)③(中国科学院大学 北京 100049)

合成孔径雷达高度计是目前测高精度最高的新一代卫星海洋雷达高度计，它将孔径合成的思想引入到传统高度计中来，测高精度比传统高度计提高了1倍。该文在对合成孔径雷达高度计与传统雷达高度计的测量精度进行比对研究的基础上，提出了机载试验数据比对处理方法，首次通过机载试验的方法验证了合成孔径高度计比传统高度计测量精度提高约1倍的结论。

合成孔径雷达高度计；精度比对；航空校飞

1 引言

雷达高度计是观测海洋的重要仪器，它能获得高精度的海面高度、有效波高和后向散射系数。它于上世纪60年代被首次提出[1,2]，在这几十年里得到了飞速的发展，其测高精度从米级逐渐提高到了厘米量级。在国际上，美国和欧洲先后发射了Seasat-A, Geosat, Topex/Posiden, ERS-1/2, Envista, Geosat, Jason-1/2/3等系列测高卫星；我国也于2011年发射了HY-2A海洋动力环境卫星，其主载荷之一双频雷达高度计的测量精度约为2~4 cm[6]。

上述星载雷达高度计都工作于传统的脉冲有限体制，受工作体制所限，其测量精度已很难再进一步提高；同时其观测的空间分辨率较低，在海岸线、近海、海冰等区域的应用有一定的局限，因此国内外的学者又提出了合成孔径雷达高度计的概念并对其进行了深入的研究[7,8]。与传统雷达高度计相比，合成孔径雷达高度计能获得更高的顺轨向分辨率和更多的有效观测视数，进而提高海面高度的测量精度[9,10]。于2010年发射的Cryosat-2卫星上的雷达高度计系统是第1台具有合成孔径试验模式的星载雷达高度计，其测量精度及分辨率明显优于传统模式；欧空局研制的Sentinel-3A卫星已于2016年2月16日发射，它的主载荷是一台真正意义上的合成孔径雷达高度计，并设计有两种工作模式：低分辨率的传统模式和高分辨率的SAR模式[14]。我国也在积极研究合成孔径雷达高度计技术[15]。

本文对星载合成孔径高度计与传统高度计的测量原理、测量精度进行了详细的比对分析和仿真，理论分析和仿真结果表明，合成孔径雷达高度计的仪器测量精度比传统雷达高度计提高大约1倍。在合成孔径雷达高度计机载试验数据的处理中，本文提出了机载试验数据比对处理方法，首次通过机载试验的方法验证了合成孔径高度计比传统高度计测量精度提高约1倍的结论，与理论分析一致，同时也验证了合成孔径高度计的数据处理算法。

2 测量机理及系统参数

雷达高度计测高的基本思想是：高度计向天底点海面发射大时带积线性调频信号，然后接收海面的回波信号，通过对回波的跟踪处理，从回波波形以及回波脉冲的精确定时中提取发射和接收信号的时间间隔，测量卫星到海面的高度值[16]。

如图1(a)，图1(b)所示，传统高度计工作在脉冲有限方式：高度计向海面发射一个窄脉冲，这个窄脉冲的海面后向散射回波被高度计接收，经过平均处理后得到一个均值为如图1(c)所示的回波波形，布朗指出该回波可以用3项卷积模型表示[16]。高度计通过测量发射脉冲到回波波形上升沿半功率点的时间延迟获得测量高度。该测量高度精度与参与平均的独立样本数有关，独立样本数越多测量精度越高。但是，单位时间内能够获得的独立脉冲数是有限的，因此传统高度计的测量精度存在一个理论的上限值[17]。

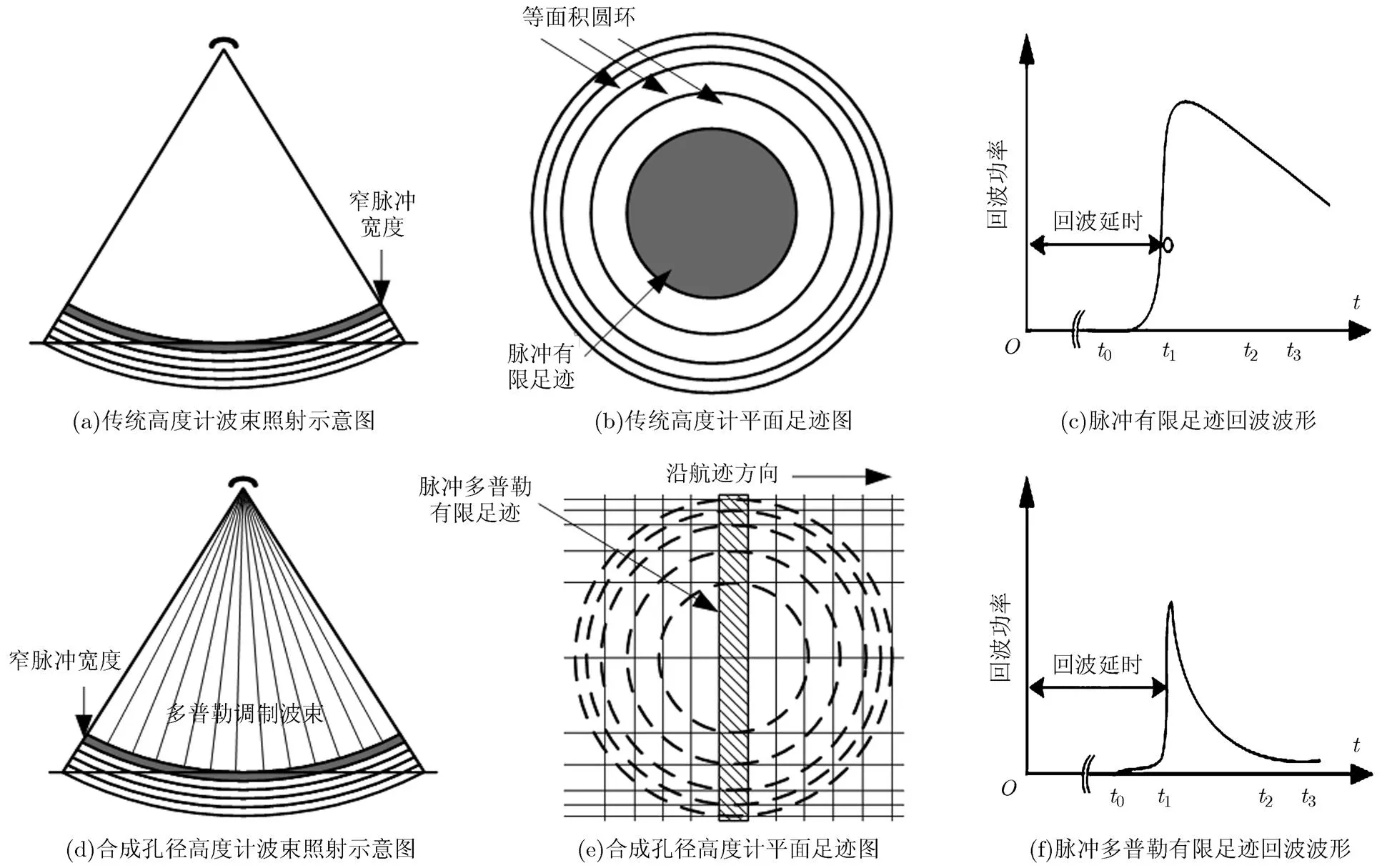
图1传统高度计与合成孔径高度计测量机理比较示意图

如图1(d)，图1(e)所示，合成孔径高度计工作在脉冲多普勒有限方式：高度计向海面发射一系列脉冲簇，脉冲簇回波经过顺轨向合成孔径处理和延迟校正[8,18]后，获得均值为如图1(f)所示的平均回波波形，该回波可以采用新的3项卷积模型表示[19,20]。合成孔径高度计同样通过测量发射脉冲到回波波形上升沿半功率点的时间延迟获得测量高度，其先进之处在于：传统雷达高度计只利用了脉冲有限足迹内的回波能量，除此之外的波束内的能量都浪费掉了；合成孔径雷达高度计在顺轨向引入了合成孔径处理，通过延迟补偿技术利用了天线波束内的全部能量，提高了有效观测次数，进而提高了测量精度。

雷达高度计测量得到的卫星到海面的高度h，还要经过精密定轨、大气、潮汐和地球物理参数的校正后才能得到海面高(Sea Surface Height, SSH)，校正过程如(1)式所示[21]。

(),h,h,h,h,SSB,SET,GOT,PT以及IB分别为：精密定轨高度、卫星到海面的高度(高度计直接测量结果)、干对流层校正、湿对流层校正、电离层校正、海况偏差校正、固体潮校正、弹性海洋潮校正、极潮校正以及逆气压校正。此时，SSH()即为海面高，其物理意义为海洋表面到大地椭球面之间的高度，它是海洋动力环境测量的重要要素。

本文所研究的是高度计仪器测量精度，即h的精度及机载试验验证结果。其中双频星载雷达高度计(Ku波段和C波段)主要系统参数如表1所示。

系统参数合成孔径雷达高度计传统雷达高度计 轨道高度(km)800800 工作频率(GHz)13.58(Ku)/5.41(C)13.58(Ku)/5.41(C) 发射脉冲峰值功率(W)10(Ku)/20(C)10(Ku)/20(C) 脉冲宽度()51.2102.4 线性调频信号带宽(kHz)320320 脉冲重复频率(MHz)182 脉冲簇重复周期(ms)11.7- 簇内脉冲数目64- 天线波束宽度1.3(Ku)/3.2(C)1.3(Ku)/3.2(C)

3 高度计仪器精度比对分析

高度计的仪器误差可分为固定偏差和随机误差，其中固定偏差可以修正，随机误差决定高度计仪器的测量精度。在分析高度计仪器精度的时候，只进行随机误差的分析。

高度计的随机误差分配到仪器的相关部件当中，由于这些误差相互独立，总的均方根误差满足：

表2传统高度计误差分配表(4 m有效波高，1s平均)

由表2可知，雷达高度计仪器精度主要由跟踪误差决定。对于传统高度计和合成孔径高度计而言，表2中的前4项误差源的大小基本一致，主要区别在于跟踪误差不同。所以在对两种体制高度计进行精度比对分析的时候，主要进行跟踪误差的精度比对分析。

3.1跟踪精度对比分析

分析合成孔径高度计与传统高度计的跟踪精度，着重于对回波模型和重跟踪算法精度的分析。

3.1.1回波的模型分析 根据文献[16]的研究，传统雷达高度计得到的海面回波模型可以表示为3项函数的卷积：

合成孔径雷达高度计对接收到的回波信号进行多谱勒延迟校正处理后[20]，每个多谱勒条带对应回波仍然满足3项卷积的形式如式(4)：

经过多视平均处理后总的回波信号形式如式(5)：

3.1.2回波重跟踪处理精度比对 雷达高度计最常用的重跟踪算法是加权最小二乘算法，根据基本原理，估计量的标准差为[21]：

式中未知量xj代表待估的雷达高度、有效波高或者后向散射系数，是协方差矩阵的元素，其中是高度计回波模型的偏导数矩阵，为加权矩阵。将雷达高度计的回波模型，以及回波噪声特性代入式(6)，即可计算得到单个回波波形重跟踪精度。

高度计重跟踪处理后，还要通过平均处理来进一步提高测量精度，一般采用1 s平均。根据式(6)，1 s平均的测量精度为

式中，a代表1 s内回波波形的独立样本数。设传统雷达高度计的脉冲重复频率为PRF，则其1 s内的独立样本数为

合成孔径雷达高度计1 s内的独立样本数为

根据上述方法，结合式(2)，计算出的传统高度计和合成孔径高度计仪器精度比对如表3所示。从表中可以看出，合成孔径高度计测高精度比传统高度计精度提高了约1倍。

表3传统高度计和合成孔径高度计理论测高精度对比(星载平台下)

3.2仿真验证

为了验证上述精度分析结果，本文对测量精度进行了计算机仿真。仿真包含3个方面的内容：第一是观测场景仿真，第二是轨道参数仿真，第三是高度计数据处理仿真。根据参考文献[22]的方法，采用海浪谱反演的方法进行了观测场景的仿真，其中风速20 m，涌浪波长600 m，涌浪波高2 m，有效波高4 m，海面网格分辨率1 m1 m；轨道和高度计仪器的仿真采用了表1中所列参数。

仿真得到的海面场景如图2(a)所示。以仿真得到的海面作为观测目标，模拟雷达高度计信号的收发过程，并分别根据传统雷达高度计和合成孔径雷达高度计的数据处理方法进行处理，最后得到仿真测量精度。图2 (b)是仿真获得的合成孔径高度计距离多普勒域延迟校正以后的回波；图3 (a)、图3 (b)分别是传统雷达高度计的平均回波和合成孔径高度计多视处理后的回波及重跟踪结果。

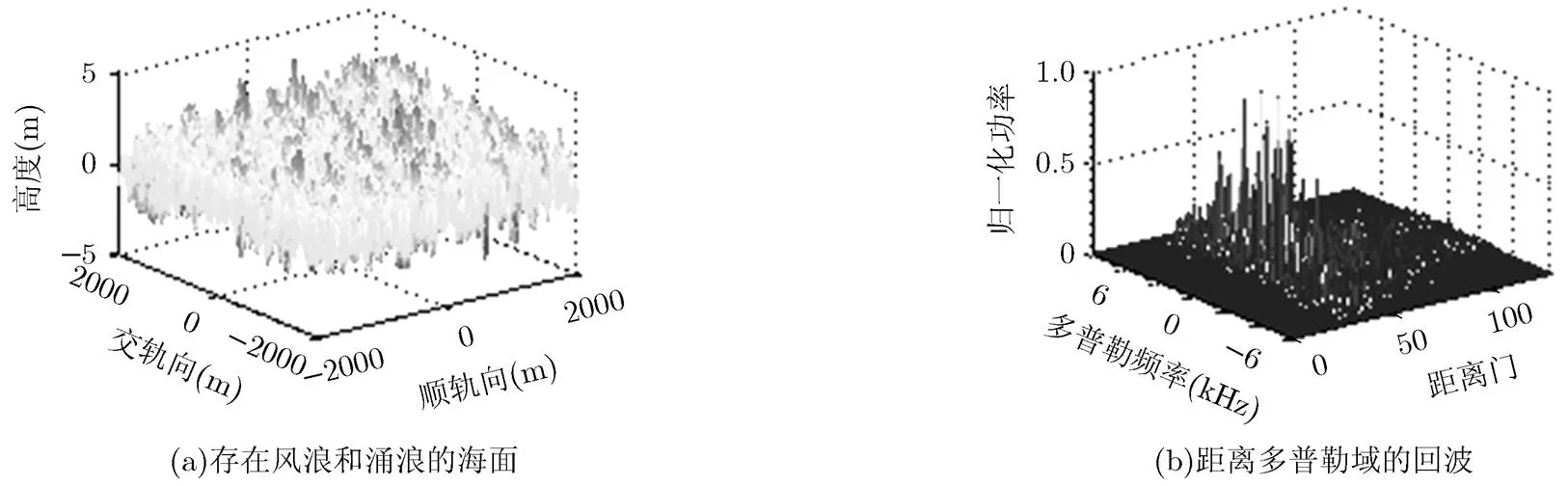
图2 仿真过程数据

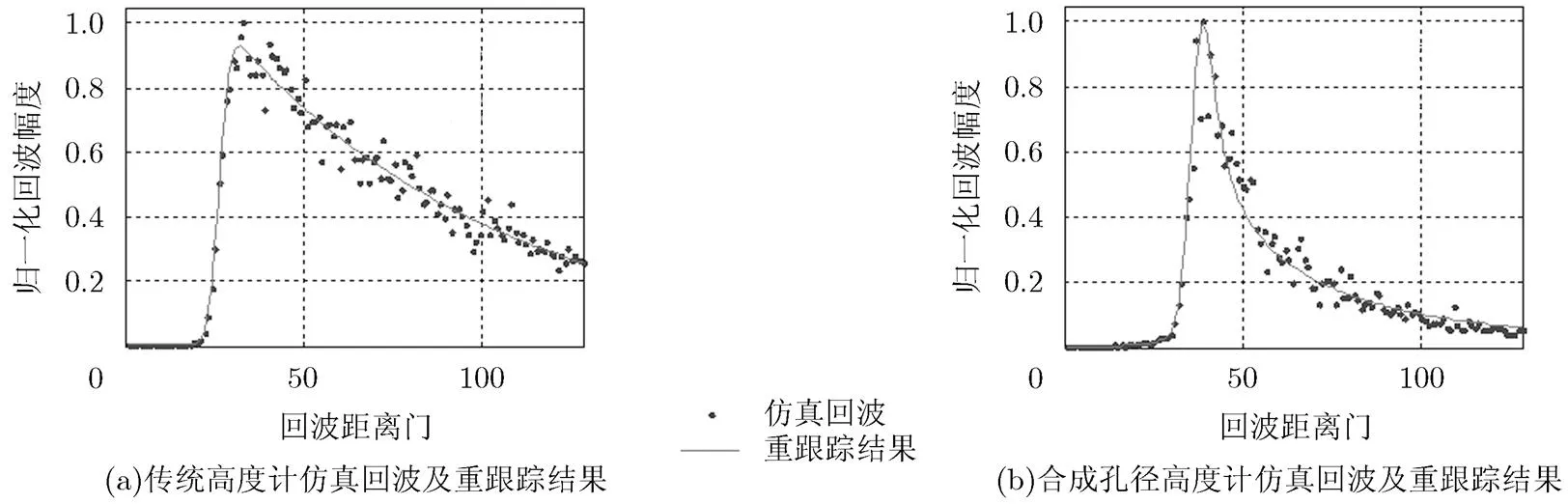
图3 高度计系统仿真回波波形及重跟踪拟合结果

表4是2 m和4 m有效波高下传统高度计和合成孔径高度计的测高精度仿真计算结果，与表3比较可知仿真结果与理论分析是基本一致的。

表4传统高度计和合成孔径高度计仿真计算测高精度对比(1s)

4 机载试验验证

在机载飞行试验中，由于飞机平台抖动很大，无法对高度计仪器直接测量结果进行精度比对。在本文中提出了通过对机载飞行试验中获得的SSH值进行精度比对，从而间接验证仪器测量精度的方法。

从式(1)可以看出，在SSH测量过程中除了高度计仪器自身误差外，还包含了其他多种误差项。在机载飞行试验中，由于飞行区域相对较小且飞行高度较低，在飞行试验区域中的干对流层校正、湿对流层校正、电离层校正、海况偏差校正、固体潮校正、弹性海洋潮校正、极潮校正以及逆气压校正都可以视为常数，所以机载模式下的SSH精度可直接表述为

4.1 机载试验仪器参数与SSH值理论测量精度估计

因机载试验的飞行高度较低，只有3600 m左右，因此机载试验的雷达高度计系统参数需要在星载参数的基础上进行调整。综合考虑机载平台高度、观测区域、多普勒频率等因素，机载设备相对于星载设备调整的主要参数见表5。

表5机载雷达高度计系统适应性调整主要参数

在机载试验中，仪器设备按表所示的合成孔径高度计参数工作，其脉冲重复频率为5 kHz。而传统高度计的有效PRF较低，在机载情况下约为500 Hz，因此可以在地面将合成孔径高度计的原始数据以1:10的比例抽取处理，进而获得传统高度计的回波数据。这样就获得了传统高度计和合成孔径高度计同一时刻对同一场景的观测数据。

根据第3节所述的精度计算方法，计算出了机载设备仪器的理论精度(对应式(14)中的)如表6所示：

表6 传统模式和合成孔径模式机载条件下仪器理论测高精度对比

在机载试验中，飞机上搭载了差分GPS来测量飞行高度(对应式(10)中的)，经过事后处理，其测量精度约为2~4 cm。根据公式(10)和表的结果，可获得机载试验中SSH的理论精度以及两种模式的精度比值，如表6所示。在机载数据处理中，如果获得的SSH的精度在表7所列的范围之内且两种模式精度之比在1.12~1.38之间，即可间接验证合成孔径高度计仪器的精度相比传统高度计提高了1倍左右。

表7传统模式和合成孔径模式机载条件下的SSH值理论精度比对

4.2 试验数据处理及结果

机载试验数据的处理分别按照传统模式和合成孔径模式的数据处理方法进行，在此不做详细介绍，只给出处理结果。图4(a)是传统模式平均回波的重跟踪结果，图4 (b)是合成孔径模式的多视回波的重跟踪结果。

图4合成孔径模式与传统模式回波的重跟踪结果

图5所示一组传统模式(SSH-CRA)、合成孔径模式(SSH-SARA)的SSH值连续测量结果，并与海洋模型计算得到的SSH值(SSH-Model)进行了对比。通过与模型的相关度分析表明，合成孔径模式的测量结果与模型的复合度更好。

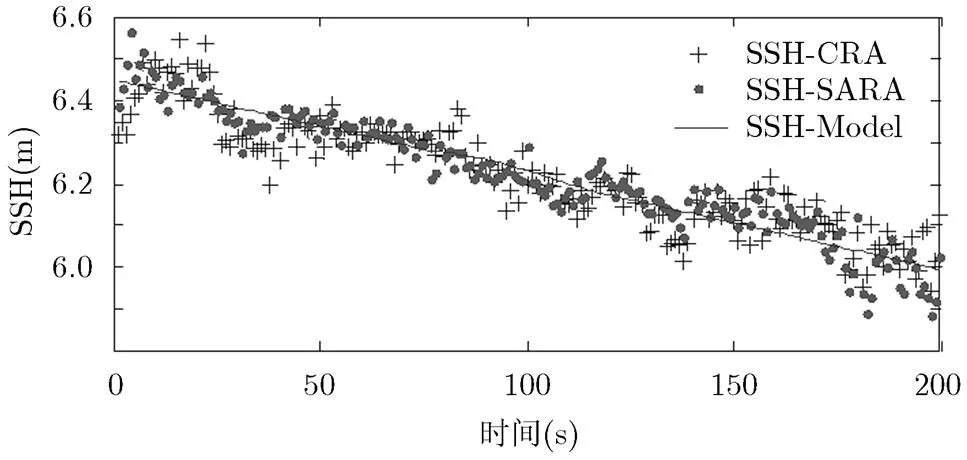
图5 合成孔径模式(SSH-SARA)、传统模式(SSH-CRA)获得的SSH值与模型(SSH-Model) 比对

表8给出了几次飞行试验中传统模式与合成孔径模式测量获得的SSH值统计精度以及两者比值。与表7的理论估计结果比较可知，试验数据处理结果在理论估计范围之内，两者之比也符合理论预计，由此可以间接验证合成孔径雷达高度计的测量精度比传统雷达高度计提高大约1倍。

表8飞行试验海面高测量精度对比

5 结论

传统雷达高度计工作于脉冲有限体制，受体制所限，其测量精度已很难进一步提高。合成孔径雷达高度计是新一代的雷达高度计，它在传统雷达高度计的基础上，在顺轨向增加了合成孔径处理，从而提高了测量的分辨率和精度。

本文对合成孔径雷达高度计与传统雷达高度计的测量精度进行比对研究，并进行了计算机仿真。提出了机载试验数据比对处理方法，首次通过机载试验的方法验证了合成孔径高度计比传统高度计测量精度提高约1倍的结论，也验证了合成孔径高度计的数据处理算法。

参考文献

[1] PIERSON WJ and MEHR E. Average return pulse form and bias for the S193 radar altimeter on Skylab as a function of wave conditions[J]., 1972,15:217-226.

[2] TOWNSEND W. An initial assessment of the performance achieved by the Seasat-1 radar altimeter[J]., 1980, 5(2): 80-92. doi: 10.1109/JOE.1980.1145459.

[3] MCGOOGAN J T, MILLER L S. BROWM G S,. The S-193 radar altimeter experiment[J]., 1974, 62(6): 793-803. doi: 10.1109/PROC.1974.9519.

[4] KOLENKIEWICZ R and MARTIN CF. Seasat altimeter height calibration[J].:(1978–2012), 1982, 87(C5): 3189-3197. doi: 10.1029/JC087iC05p03189.

[5] WATSON C, COLEMAN R, White N,. Absolute calibration of TOPEX/Poseidon and Jason-1 using GPS buoys in Bass Strait, Australia special issue: Jason-1 calibration/validation[J]., 2003, 26(3/4): 285-304. doi: 10.1080/714044522.

[6] BAO Lifeng, GAO Peng, PENG Hailong,. First accuracy assessment of the HY-2A altimeter sea surface height observations: cross-calibration results[J]., 2015, 55(1):90-105. doi: 10.1016/j.asr.2014.09.034.

[7] RANEY RK. A delay/Doppler radar altimeter for ice sheet monitoring[C].Proceedings of the International Geoscience and Remote Sensing Symposium, Italy, 1995, 2: 862-864. doi:10.1109/IGARSS.1995.521080.

[8] RANEY R K. The delay/Doppler radar altimeter[J]., 1998, 36(5): 1578-1588.doi: 10.1109/36.718861.

[9] HALIMI A, MAILHES C, TOURNERET J Y,. Cramér-Rao bounds and estimation algorithms for delay/Doppler and conventional altimetry[C]. Signal Processing Conference (EUSIPCO), 2013 Proceedings of the 21st European, Marrakech, 2013: 1-5.

[10] JENSEN J R and RANEY R K. Delay/Doppler radar altimeter: better measurement precision[C]. International Geoscience and Remote Sensing Symposium, Washington,America,1998, 1998,4: 2011-2013.doi: 10.1109/IGARSS.1998.703724.

[11] SCAGLIOLA M, FORNARI M , TAGLIANI N,. Pitch estimation for CryoSat by analysis of stacks of single-look echoes[J].,2015, 12(7): 1561-1565.doi: 10.1109/LGRS.2015.2413135.

[12] JAIN M, MARTIN-PUIG C, ANDERSEN O B,. Evaluation of SAMOSA3 adapted retracker using Cryosat-2 SAR altimetry data over the Arctic ocean[C]. Proceedings of the International Geoscience and Remote Sensing Symposium, Quebec, Canada,2014: 5115-5118. doi: 10.1109/IGARSS.2014.6947648.

[13] GALIN N, WINGHAM D J, CULLEN R,. Measuring the pitch of CryoSat-2 using the SAR mode of the SIRAL altimeter[J]., 2014, 11(8):1399-1403. doi: 10.1109/LGRS.2013.2293960.

[14] DONLON C, BERRUTI B, MECKLENBURG S,. The copernicus Sentinel-3 mission and oceanography: overview and current status[C].Egu General Assembly Conference Abstracts, Vienna,Austria,2014,16:1869.

[15] XU Ke, LIU Peng, SHI Lingwei,. The altimeter precision comparison between SAR mode and conventional mode through airborne experiment[C]. Proceedings of the International Geoscience and Remote Sensing Symposium, Milan, Italy, 2015: 3638-3641.doi: 10.1109/IGARSS.2015.7326610.

[16] BROWN G S. The average impulse response of a rough surface and its applications[J]., 1977, 25(1): 67-74.doi: 10.1109/TAP.1977.1141536.

[17] 许可. 高分辨率星载雷达高度计系统研究[D].[博士论文]，中国科学院研究生院(空间科学与应用研究中心), 2001.

XU Ke. Study on high resolution spaceborne radar altimeter [D]. [Ph.D. dissertation], Graduate University of the Chinese Academy of Sciences(Center for Space Science and Applied Research), 2001.

[18] RAY C, MARTIN-PUIG C, CLARIZIA M P,. SAR altimeter backscattered waveform model[J]., 2015, 53(2): 911-919.doi: 10.1109/TGRS.2014.2330423.

[19] HALIMI A, MAILHES C, TOURNERET J Y,. A semi-analytical model for delay/Doppler altimetry andits estimation algorithm[J]., 2014, 52(7): 4248-4258.doi: 10.1109/TGRS.2013.2280595.

[20] 杨双宝. 基于合成孔径技术的高精度雷达高度计技术研究 [D].[博士论文], 中国科学院研究生院(空间科学与应用研究中心), 2007.

YANG Shuanbao. Study on high precision synthetic aperture radar altimeter technology[D]. [Ph.D. dissertation], Graduate University of the Chinese Academy of Sciences(Center for Space Science and Applied Research), 2007.

[21] 徐曦煜. 星载雷达高度计误差分析和定标技术研究[D].[博士论文]，中国科学院研究生院(空间科学与应用研究中心), 2007.

XU Xiyu. Study on spaceborne radar altimeter error analysis and calibration technology[D]. [Ph.D. dissertation], Graduate University of the Chinese Academy of Sciences(Center for Space Science and Applied Research), 2008.

[22] 王磊. 高精度卫星雷达高度计数据处理技术研究 [D].[博士论文]，中国科学院研究生院(空间科学与应用研究中心), 2015.

WANG Lei. Study on the data processing for high precision satellite radar altimeter[D]. [Ph.D. dissertation], Graduate University of the Chinese Academy of Sciences (National Space Science Center), 2015.

Precision Comparison and Airborne Experiment Validation between SAR Altimeter and Conventional Altimeter

LIU Peng①②③XU Ke①②WANG Lei①②SHI Lingwei①②YU Xiufen①②

①(,,100190,)②(,,100190,)③(,100049,)

Synthetic Aperture Radar ALtimeter (SARAL) is a new generation radar altimeter and has the best height precision now. As using synthetic aperture technique, the height precision of SARAL is improved by one fold. Based on studying the height precision of Conventional Radar Altimeter (CRA) and SARAL, a novel comparison method is developed to process the airborne flight experiment data. And the precision comparison result shows that the height precision of SARAL is increased by one fold.

Synthetic Aperture Radar ALtimeter (SARAL); Precision comparison; Airborne flight experiment

TN953

A

1009-5896(2016)10-2495-07

10.11999/JEIT151354

2015-12-01；改回日期：2016-06-08；网络出版：2016-07-19

许可 xuke@mirslab.cn

刘 鹏： 男，1983 年生，博士生，研究方向为雷达高度计系统技术、数字信号处理.

许 可： 男，1967 年生，博士，研究员，博士生导师，主要研究方向为星载雷达高度计系统技术、合成孔径雷达高度计系统技术、信号处理技术、电路和软件技术.

王 磊： 男，1986 年生，博士，研究方向为雷达高度计信号处理.

史灵卫： 男，1980 年生，博士，研究方向为雷达高度计数据处理.

于秀芬： 女，1980 年生，硕士，研究方向为数字信号处理.