动中寓静，寻求突破—例说中考数学压轴题中求面积最值问题的解法分析

江苏省徐州市第十三中学 王 宁

中考数学试卷中的压轴题一直备受关注，压轴题在中考试卷中凸显选拔功能，位于试卷的最后部分，属于跨领域问题，思维层次较高，区分度大，综合运用多方面知识解决，对考生的数学素养提出了较高的要求，需要考生抓住变化中的不变量，注重对考生动手能力和自主探索能力的考查。而考生要想达到此能力状态，不仅需要平时的积累，更需要能看透出题人设置的启发引导、逐层递进的问题串，极大地考查了考生的考场学习力。压轴题一般由三问组成，第一问容易上手，得分率在0.8 以上，第二问稍难，得分率在0.6～0.7 之间，第三问难度较大，得分率在0.3～0.4 之间。要想多得分，必须要有科学的分析问题的方法，善于总结压轴题中蕴含的思想方法，比如数形结合思想、分类讨论思想、方程思想、转化思想等等，寻求解题思路时切忌套用机械的模式，而应从不同的角度识别题目中的条件和隐含信息、图形的几何特征，发现数量之间的关系，计算时要有耐心，不能急于求成，调整好心态去争取更多的得分。常见的压轴题类型很多，有动态几何问题、多种函数交叉问题、几何图形归纳猜想问题、阅读理解问题、最值问题、定值问题、存在性问题等等。下面笔者选取了一道求面积最值的压轴题，结合教学中学生的多种思路进行分析，希望可以给学生在解这类题型时提供一些帮助。

【题目】如图，矩形ABCD的边AB=3cm，AD=4cm， 点E从点A出发，沿射线AD移动。以CE为直径作⊙O，点F为⊙O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与⊙O相交于点G，连接CG。

（1）试说明四边形EFCG是矩形。

（2）①当⊙O与射线BD相切时，点E停止移动。在点E的移动过程中，矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由。

② 求点G移动路线的长。

【分析】这道压轴题考查了矩形背景下动圆的运动变化，需要运用函数思想解决面积的最值问题。本题有效考查了学生对圆的有关性质、矩形的性质与判定、相似三角形的性质与判定、锐角三角函数的概念、勾股定理、垂线段最短等知识的掌握情况，同时也关注到了初高中知识的有效衔接。

【第一问解析】∵CE是⊙O的直径，点F、G在⊙O上，

∴∠EFG=∠EGC=90°。

又∵EG⊥EF，即∠FEG=90°，

∴四边形EFCG是矩形。

【分析】第一问比较简单，要求证明在已知一个直角且以圆的直径为一条对角线的四边形是矩形，也为第二问探索矩形面积的最值问题作了铺垫。需要用到“直径所对的圆周角是直角”“有三个角是直角的四边形是矩形”这两个定理，多数学生可以顺利完成。

【第二问解析】①∵四边形ABCD是矩形，∴∠BAD=90°，∴∠BAD=∠FEG=90°。

又∵∠ADB=∠FCE，∴△ABD∽△FEC，∴EF∶CF∶CE=3∶4∶5。

当点F与点B重合时，CF=BC=4；

当⊙O与射线BD相切时，点F与点D重合，CF=CD=3；

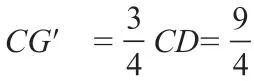
【分析】第二问难度较大，分为两个小问。第一小问是在变化的过程中求面积的最值问题。题目设置了由一个动点E引起了线段CE的变化，导致以CE为直径的圆的面积变化，从而带动了圆的内接矩形面积的变化。问题的设置引导学生探究隐藏在“伸缩的圆”和“变化的矩形”中“不变”的数学结论和“变化”的数学规律，让学生在探究的过程中充分感受数学是研究数量关系和空间形式的一门科学。因此，解决这个问题要运用函数的思想，先设置一个自变量，然后用这个自变量表示矩形的面积，根据函数关系式观察有没有最值，这里要先求出自变量的取值范围，再求出最值。而实际上，许多学生都能判断出矩形面积的最大值和最小值在什么位置，并求出最值，但是他们没有说明出现最值的理由，只属于合情推理的范畴，没有上升到用函数来分析解决问题的层面，因此失分较多。由于题目没有像常规的动点题那样给出动点的运动时间和速度，导致学生不知道如何设置自变量，不过这也是命题者高明的地方，给学生自由发挥的空间，让他们自己去发现、去探索。

基于以上分析，第一步可设置的自变量有许多种，笔者在教学中发现学生的解法较多，整理下来可分为以下几类：①设AE=x或DE=x；②设EF=x，或CF=x；③设CE=x；④设BF=x。第二步用自变量表示矩形的面积，S矩形EFCG=EF·CF，这里需要用含x的式子表示EF 和CF，而发现EF 和CF 的关系是关键，也是突破口，需要用到△ABD ∽△FEC 或运用等角的三角函数比值相等，找到EF ∶CF ∶CE=3 ∶4 ∶5，然后用一个变量来表示矩形面积，。

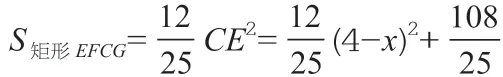
第二小问是求点G移动路线的长，只要知道点G的运动轨迹就可以了，由于∠CDG=∠CEG，而∠CEG是不变的，所以∠CDG也是固定的，当⊙O与射线BD相切时，点F与点D重合，此时∠DCG=90°，而此时的DG就是点G移动路线的长，利用勾股定理即可求出。

【教学反思】本题以“矩形EFCG的变化”为核心问题，以问题串的形式围绕核心问题进行设问，层次递进，环环相扣，在学生对核心问题步步深入的过程中，较好地体现了对基础知识、基本技能、基本思想、基本活动经验的考查，同时渗透了分类、数形结合、函数、转化和特殊化等数学思想和方法，在学生经历观察、实验、猜测、计算、推理、验证的过程中，突出考查了学生的数学思维品质和综合运用所学知识发现和提出问题、分析和解决问题的能力。另外，本题解决方法的多样性充分尊重了学生思维的个性差异，这样的设计充分体现了课标倡导的“不同的人在数学上得到不同的发展”这一基本理念，使得本题具有了良好的效度和区分度，毫无疑问，这道求面积最值的压轴题极具代表性，分析透彻这道题可以帮助学生掌握这一类题型的解法。