辩证思维视角下的高中数学教学

江苏省清浦中学 赵雪飞

辩证法是一种重要的思维方法，是高中生理解数学知识或解决数学问题中不可或缺的一种思维工具。如果离开了辩证法，那么学生就无法有效解决相关数学问题，更无法促使学生形成良好的数学核心素养，所以强化辩证思维在数学教学中的渗透与应用显得尤为重要。因此，为了提升高中生的数学解题能力，有必要对辩证思维的应用策略进行深入探讨。

一、深挖数学教材，揭示辩证数学关系

数学知识源于生产实践而又广泛应用于科学技术、生产生活等领域，其中包含着有关数量关系和空间形式等的知识。基于辩证唯物主义视角，结合数学的上述知识特性，可以深刻地把握与掌握数学知识当中包含的辩证关系，以此发展他们的辩证思维能力。因此，在数学教学期间，教师要注意深入地挖掘数学教材中有关辩证主义的数学概念等相关知识，以此促进学生辩证思维能力的发展。

例如，在数学学习期间，学生通过学习“负数”的概念，可以改变以往学生思想中存在的“小自然数无法减去大自然数”的思想；通过学习“分数”，可以改变以往学生存在的“整数之间无法整除”的思想；通过学习“无理数”，可以改变以往学生存在的“负数无法开偶次方”的思想，这些相关数学概念都是数学知识中辩证思维应用的具体体现。此外，在将数的概念扩充到实数域后，虽然可以确保数的连续性，解决数的基本四则运算，但是却失去了有理数的可数性特性等，挖掘数学教材中这些辩证思维的知识可以深化学生对数学知识的理解，同时也有利于促使学生更好地找到矛盾解决方法，促使他们形成正确的思维观念。

数学学习离不开辩证思维，教师在数学教学中要善于挖掘教材中的资源，培养学生的辩证思维，提升学生的数学思维品质。为此，教师要养成发现的慧眼，在点滴之中提升学生的数学能力。

二、基于化静为动，培养正确的运动观

动与静二者是一对具有辩证关系的矛盾概念，分别代表了某种事物的不同极端或相反状态。在这两种状态下，静是一种相对状态，动则是一种绝对状态。前者是指事物保持停止不动的状态，而后者则主要反映出事物的内在本质与特征。所以在高中生学习数学知识的过程中，要立足于相对静止的状态，不断探索数学问题中所包含事物的动态化运动轨迹。此外，在高中生对事物运动过程进行仔细观察期间，也必须要充分意识到运动与静止二者的相互转化关系，力求可以切实牢固地树立和应用“静中有动”“动中有静”和“动静结合”等一些辩证思维方法。

例1：已知某圆的方程为x2+y2-4x-8y+15=0，试求与该圆相切在A（3,6）点且经过B（5，6）点的圆的方程。

解析：针对该道数学问题，如果可以先假定待求圆的方程，之后采取变静为动的方式，通过动态的变化，找寻二者的切点，那么对提高解题效果会产生积极影响。

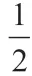
三、基于数形结合，渗透对立统一观念

数与形二者是构成数学知识的两种基本形式，共同实现了对不同事物的运动规律或特性进行客观展示。其中,数可以对相关事物或现象进行定量描述，而形则能够对客观事物或现象的形式进行展示，它们相互之间呈现联系而又对立的关系，并且可以在一定程度上实现相互转换的作用。在高中数学教学过程中，数学教师要善于利用数形结合、以形思数或以数想形等来深刻地把握和掌握有关问题的内在变化规律，最终可以在其中相应地渗透对立统一概念，这对提高学生的思辨思维产生积极影响。

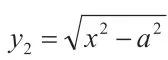
总之，辩证思维是提高高中生数学思维能力的一个重要数学方法，也是学生数学素养的重要标志。在高中数学教学中渗透辩证思维教学，可以深挖数学教材中的辩证思维知识，同时还要注意基于化静为动，培养正确的运动观;基于数形结合，渗透对立统一观念，力求以此提高学生的数学思维能力，真正实现提升学生数学素养的目的。