基于核心素养的高中数学创新思维培养对策

江苏省吴江高级中学 梁秋健

近年来，随着新课程改革理念的不断深入人心，核心素养逐渐得到教育界的广泛认可。核心素养以培养学生掌握适应终身学习和社会发展所需要的关键能力为目标，推动着新课程改革的不断完善。当前，我国正处于大众创新、万众创业的局面下，对人才的创新能力、团队协作能力有着越来越高的要求。因此，按照核心素养要求，对高中数学教学实施教学改革和创新，不断提高学生的数学创新思维能力有着非常重要的意义。

一、核心素养对高中数学创新思维的教学启示

核心素养对高中数学教学有着重要的启示，为教师的高中数学教学指明了方向。按照核心素养要求，对高中数学课堂教学的创新思维的启示主要包括：

1.要积极培养学生的创新能力

创新是人类社会不断进步的动力。数学是一门重要的基础学科，是对人们认识世界和改造世界的重要工具。当前，科技日新月异，经济社会快速发展，这都离不开数学的支持，更离不开高素质的创新型人才的支持。因此，按照核心素养要求，高中数学教学中务必要重视培养学生的创新能力，培养学生的创新性数学思维，鼓励学生在数学知识的海洋中不断创新。

2.要积极培养学生的自主学习能力

自主学习能力是指学生能根据自身的知识储备和学习习惯，合理安排时间，制订适合自身的学习计划。在高中数学教学中积极培养学生的学习自主性，给学生较大的学习空间，使学生具备自我管理、自我评价、自我调节和自我总结的能力，改变过去依靠老师或家长安排的局面。自主性不仅能帮助学生养成良好的学习习惯，还能使学生在自主学习中获得很多课本之外的知识。

3.要积极培养学生的实践能力

实践能力是指学生利用所学知识解决生活中实际问题的能力。学以致用是所有知识学习的最终目的，数学知识在日常生活中有较为广泛的应用，教师在教学中可以将生活中的很多案例引入课堂教学，使学生认识到数学知识的巨大应用价值和独特魅力，提高学生的实践能力，全面提升学生的综合素质。

在高中数学教学中贯彻核心素养理念，务必要培养学生较好的创新能力、自主学习能力和实践能力。

二、基于核心素养的高中数学创新思维培养策略

创新是一个民族进步的灵魂，是国家与民族的核心竞争力。严格按照核心素养要求培养学生的创新思维，并利用创新思维分析问题、解决问题，全面提高学生的综合素质。

1.创设问题教学情境，引导学生发散思维

问题教学情境能很好地吸引学生的注意力，促使学生对问题积极思考、发散思维，进而对问题的解决方法进行探究，引导学生发散思维空间。一名优秀的教师在教学中应根据教学内容精心设计教案，积极创设问题教学情境，引导学生发散思维，提高学生的创新思维能力。

通过创设问题教学情境，能够很好地吸引学生的注意力，拓展学生思维空间，发散学生思维，提高学生的创新思维意识。教师不仅要在课堂开始时创设问题情境，在下课时还可以为下一次课程教学内容创设情境，要求学生在课下进行思考并尝试解决，为下一堂课埋下伏笔。

2.应用数形结合思想，拓展学生思维空间

数形结合思想是中一种常见的数学思想，对拓展学生思维有着非常好的效果。在教学中，可以通过以数化形、以形变数或形数互换的方法来应用。在讲解一些较为抽象的知识时，通过图表可以很直观地将知识转化为图像，帮助学生很好地掌握知识。如在讲解函数极值计算时，可以根据函数表达式绘制出图形，从图形上观察出函数的极值分布，再通过数值求解的方式求解出极值。以形变数是几何教学中常见的方法，通过对图形的分析找出其中隐含的条件，并在此基础上进行求解。当两者都较为熟练后，形数互换可以综合上述两种优势，不仅可以将函数转化为直角坐标系中的图形进行分析，还可以将坐标系中的图形转变为函数进行求解。

例2：函数f（x）=2sinπx-x+1 的所有零点的和为——。

分析：零点数即为方程2sinπx-x+1=0 的解，直接求解较为困难。当f（x）=0 时，可得2sinπx=x-1，若能构造两个函数y1=2sinπx、y2=x-1，则本题的求解转化为曲线y1=2sinπx与y2=x-1 的交点的横坐标的和。

作图如右图所示，可以发现共有5 个交点，且关于点（1，0）对称，即函数f（x）的所有零点的和为5。

这种数形互换的方式能够有效拓展学生的思维空间，当学生熟练掌握数形结合思想后，学生可以在函数表达式与二维平面或三维空间中灵活切换，转换自如。

3.积极引导学生自行思考，构建适合自身的思维模式

“授人以鱼不如授人以渔”。在高中数学教学中，要积极引导学生自行思考，向学生传授自我学习、自我思考的方法。学生在掌握基本数学分析和数学思维能力的基础上，对数学问题自行思考，掌握独立分析数学问题、解决数学问题的能力。要将学生从传统的思维模式中解放出来，鼓励学生不断试错、不断反思和不断总结，充分提高学生的数学思维能力。在教学中，教师可以设置一些开放性的问题，让学生尝试自行思考，鼓励学生探索各种可能的结论，之后再与学生进行交流。

例如在讲解“黄金分割法”时，可以通过投影仪展示基于黄金分割原理设计的建筑、各类商品等图形，使学生认识到黄金分割的魅力，同时还可以要求学生举例自己生活中的黄金分割法的应用案例。在交流过程中要对学生独立思考的行为进行鼓励，即使出错也无需责怪，使学生逐渐形成适合自身的思维模式。学生如能构建适合自身的思维模式，对学生养成自我学习、终身学习的能力有着事半功倍的效果。

4.结合实践案例，训练创新思维

数学是一门实践性的课程，是各类理工类学科的基础。通过数学实践案例，可以使学生认识到数学在各个行业中的应用，可以有效训练学生的创新思维。

例3：某房地产开发商投入3240 万元拍得一块办公用地，计划在该地块上建造一栋至少10 层、每层为3000 平方米的写字楼。经测算，若该写字楼建造x层，每平方的平均建筑费用为（750+48x）元，为了使写字楼每平方米的总成本最低，则应该建设多少层？

分析：该题是一个极值问题。每平方的总费用应为建造费用和购买地价之和。令每平方米的总成本为y元，则有：

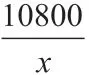
通过实践案例题，不仅可以训练学生的数学知识应用能力，还能使学生认识到数学在社会各行业中的广泛应用，使学生认识到数学的巨大魅力，拓展学生的视野，有效训练学生的创新思维。

在核心素养理念下指导高中数学教学，以提高学生的创新思维为目标，以此为基础充分发散学生的思维方式，拓展学生的数学思维空间，训练学生的数学思维能力，构建适合自身的数学思维方式。数学创新思维是现代科学思维的创新基础，培养学生良好的数学创新思维方式，激发学生强烈的求知欲望，赋予学生无限的潜力，为学生进入大学或社会后进一步应用数学知识打下良好的基础。高中数学教师应按照核心素养理念要求，不断更新教学理念，创新教学模式，全面提高学生的数学创新思维教学成效。