传感器网络分布式事件触发多目标估计

张玲玲,张 亚

(东南大学自动化学院,江苏南京 210096;复杂工程系统测量与控制教育部重点实验室,江苏南京 210096)

1 引言

无线传感器网络是由大量自组织的传感器节点所构成,每个传感器节点能够发送接收并对数据进行处理,并通过节点之间的相互协作完成诸如智能监测、无人机编队、目标跟踪等任务的复杂网络[1–3].基于无线传感器网络技术的目标跟踪问题是无线传感器网络在实际中的一项重要应用,通常需要对线性或非线性动力学的系统状态进行连续地估计.而能量消耗作为另外一个重要方面在设计算法时也应该被着重考虑.然而这两方面之间存在一定的矛盾:从一方面来说,能够测量到目标的节点越多,网络的跟踪误差越小(不考虑其他因素);但是驱动节点所消耗的能量也越多,这对于传感器网络来说是不利的.考虑到网络中节点的能量是有限的,总是希望传感器网络所消耗的能量越少越好,从而在一定程度上延长网络的生命周期保证网络的稳定性.

如果从监测区域中的目标个数来分的话,可以将目标跟踪问题分为单目标跟踪问题和多目标跟踪问题.在一般的多目标跟踪(multi-target tracking,MTT)系统中,不仅目标的状态随时间变化,而且由于目标的出现和消失导致目标的数目也在发生变化.即使在检测到所有目标且没有错误检测的特殊情况下,经典的滤波方法也不能直接应用,因为没有关于哪个目标生成了哪个测量值的信息.除了在动态过程和测量中的噪声带来的不确定性之外,需要亟待解决的问题就是数据关联问题即将节点接收到的多个目标的测量值和目标之间建立对应关系.目前分布式多目标跟踪方面的滤波算法已有不少[4–10],包括贝叶斯滤波[6]、蒙特卡洛数据关联法[7]、一致性随机集滤波[9]等.在分布式随机集滤波器解决传感网多目标跟踪问题中,近年来引起较多关注的有几何均值融合和算术均值融合算法可以应对节点间未知关联的融合模式[10].近年来,聚类算法已经有了进一步发展并应用于解决MTT中的数据关联问题[11–18].文献[11–13]研究了分布式网络的数据聚类问题,以克服集中式聚类方法由于隐私和安全问题或者技术限制在大型动态分布式对等网络中进行数据聚类时存在的局限性.通过在每个节点上协同进行分布式聚类来逼近集中式聚类最优解.一方面通过采用约剪技术来减少运行时间,另一方面通过属性加权技术提高聚类效果.Wang等人[14]针对无线传感器网络中基于距离的多目标跟踪问题,提出了一种新的进化核聚类算法将每个时刻的传感器测量数据和对应的目标关联起来.通过对比实验的跟踪结果表明,该算法对较大的定位误差具有较强的鲁棒性.He 等人[15–16]则将DBCAN聚类算法和JPDAF算法相结合提出了一种基于传感器网络的新型联合多目标跟踪保持算法.Li等人[17–18]设计多传感器协作聚类方法实现分布式目标探测或者去除杂波、漏检等.Kamal等人[19]研究了计算机视觉领域中分布式摄像头网络的多目标跟踪问题,提出了一种信息加权的一致性分布式多目标跟踪算法(multi-target information consensus,MTIC)来解决数据关联问题.尽管多目标跟踪方面已经有了很多有效的算法,但上述算法在设计时都没有考虑节点能耗的问题.

最近,基于事件触发的估计方法在减少网络能量消耗方面有巨大的潜力,打破了传统周期性采样的弊端[20–26].Weimer和Araújo等人[20]为状态估计问题提出了全局事件触发的通信策略,能够在满足估计器性能的条件下来最小化网络能量消耗和通信传输次数的加权函数.针对所提出的的全局最小化问题引入分布式1步贪心启发算法求解从而使得传感器仅使用自身和邻居节点的信息来确定它们各自的通信触发策略.尽管该方法是分布式的且考虑到传感器网络能量和带宽是有限的,然而没有考虑到节点的感知能量受限这一事实且仅针对单个线性过程有效.Trimpe和D’Andrea[21]研究了一种基于事件的状态估计方法,其中多个传感器通过公共总线将测量数据传输到中央处理器,并通过分析切换Raccati方程的收敛性证明了该方法的有效性.然而该方法假设存在一个中央估计器并不是分布式的.Molin 和Hirche[23]研究了线性系统的基于事件触发估计的最优设计,为了得到在有限时间范围内均方估计误差和网络期望传输次数之间的最佳权衡提出了一种基于坐标下降的迭代算法.尽管该方法几乎是最优的,但仅对线性系统使用且要求系统统计不确定性的分布是正态且单峰的.Battistelli等人[24]提出了一种新的基于事件触发通信的一致性卡尔曼滤波算法,该事件触发通信策略通过强制每个节点只在被判断为触发时才向邻居节点传输本地信息从而提高能源效率延长网络寿命,但是该算法没有考虑节点的感知能力受限的问题并且仅针对单个目标有效.目前,基于事件触发的传感器网络分布式估计问题大多只考虑单个目标,而且在设计分布式算法时通常假设节点对目标的测量情况是不变的.然而,对传感器网络来说,其监测区域内会存在多个移动的目标,而且由于节点测量范围有限,测量拓扑不可避免地会发生改变.对节点来说,不仅需要考虑通信能耗设计通信触发机制,还应该设计测量触发机制节省节点测量能耗.

本文主要研究传感器网络中多个移动目标的分布式估计问题,针对目标数目已知且在整个跟踪过程目标数目固定的场景提出了一种完全分布式的基于事件触发测量、通信机制和k-means聚类的多目标滤波算法.采用k-means聚类算法解决多目标跟踪的数据关联问题,紧接着设计了一种完全分布式的(仅需要邻居节点的信息而不需要全局信息)事件触发测量和通信策略来实现网络跟踪误差和能量消耗之间更好的权衡,最后提出了基于最小迹融合原则的卡尔曼滤波算法实现对多个目标的跟踪.本文的主要创新点在于提出一种完全分布式的测量和通信事件触发机制来权衡跟踪误差和能量消耗.

2 问题描述

假设监测区域内总共存在NT个待跟踪目标,考虑具有如下线性离散时间动态系统的第t个运动目标:

假设网络中共有N个传感器节点,第i个传感器节点对第t个目标的测量方程为

考虑k时刻节点i对第t个目标的性能指标为Ji(k),那么针对多目标的优化问题定义如下:

其中:i,j=1,2,…,N,t=1,,…,NT,N是部署在网络中的节点总数,T是总的采样时间,NT是总的跟踪目标个数.约束条件(4)的含义是节点的通信半径是有限的,即两个通信的邻居节点i和j之间的距离dij必须在通信半径Rc之内,Ni=Ni ∪i表示节点i的邻居节点集合且i∈Ni.也就是说,如果(i,j)∈E且(j,i)∈E当且仅当dijRc,因此网络的通信拓扑是无向的.约束条件(5)的含义则是节点的测量半径也是受限的.即在第k个采样时刻只有当目标t和节点i之间的距离dit不超过节点i的测量半径Rs时才能测量到目标.本文用表示在第k个采样时刻目标t是否在节点i的测量范围之内:表示目标t在节点i的测量范围之内;否则

这里用ci(k)∈{0,1}表示节点i第k个采样时刻根据事件触发通信策略判断得到的是否将信息发送给邻居的二值标志变量,用ϕi(k)∈{0,1}表示节点i在第k个采样时刻根据事件触发测量策略判断的是否触发测量的二值标志变量,用∈{0,1}表示第i个节点是否成功测量到目标t的二值标志标量.不难理解,=1当且仅当在第k个采样时刻目标t在节点i的测量范围之内即=1和第k个采样时刻节点i触发测量即ϕi(k)=1同时成立.因此,可以得到三者之间的关系是

综合考虑跟踪误差和能量消耗两个方面的系统性能指标Ji(k)[22–23]的定义如下:

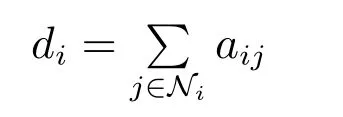
是节点i的邻居节点的个数,ws>0和wc>0分别是测量和通信能量加权值,Es和Ec是分别代表测量和通信能量消耗.

性能指标(6)主要由节点对目标估计协方差的迹和能量消耗两部分组成.当节点触发测量时,其估计协方差可能减小但测量能耗增加;同样的当节点向其邻居发送数据时,其邻居的协方差可能减小但通信能耗增加.

本文的一个主要工作就是设计测量和通信触发机制使得性能指标尽可能小.

3 主要结果

3.1 基于事件触发测量和通信策略的分布式多目标跟踪算法

本小节主要结合聚类算法,提出了基于事件触发测量和通信策略的分布式卡尔曼滤波算法来对多个目标进行估计跟踪.

首先阐述将测量数据和估计轨迹曲线进行关联的k-means聚类算法.定义节点i在第k个采样时刻接收邻居节点j的信息之后的测量值集合为

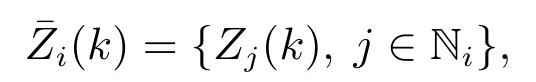
1)初始化:在第k个采样时刻随机初始化NT个聚类中心µ1(k),µ2(k),…,µNT(k)∈q;

2)重复直到收敛:对于每个测量值样本ii按照最小距离准则分配给NT个聚类中心中的一个,然后重新计算NT个类簇的新聚类中心即

其中:ccii(k)代表k时刻第ii个测量值样本的类簇标签,1{·}表示指示器函数即如果括号中的条件成立取值为1;否则取值为0.

收敛的判断条件为每个测量值样本的类簇标签不再发生变化或者达到最大迭代次数.k-means算法的特点是聚类中心是用各个类簇中所有测量值数据的平均值表示.

注1用k-means聚类算法来解决多目标跟踪(MTT)的数据关联问题时,需要事先指定k-means算法中的参数K即类簇的个数,因此结合k-means聚类的多目标跟踪算法仅适用于目标数目已知且固定的MTT问题.由于事件触发测量和通信策略的引入,导致可能存在在某个采样时刻节点自身及其邻居的测量值集合的数目小于类簇的个数K的情况,在此种情况下无法执行k-means聚类算法,而仅对每个跟踪目标的状态估计和协方差做一步预测.

在k+1个采样时刻到来之前,每个节点首先按照加权平均策略对邻居信息进行融合.定义和分别表示节点i利用邻居信息进行融合得到对第t个目标的融合先验状态估计和协方差矩阵,即[27–28]

这里,本文采用基于最小迹原则的融合策略:简单来说就是每个节点都直接跟随自己和邻居节点中协方差矩阵的迹最小的那个节点.因此,式(10)–(11)中的权重可以这样设计:

然后执行如第3.1节所示的k-means聚类算法将所有邻居(包括自身)的测量值和其对应的目标关联起来.取k时刻目标t对应的聚类中心(k)作为所有对目标t的测量值的融合,并按照下式更新目标t的后验状态估计(k|k)和后验协方差矩阵(k|k):

如果k时刻节点i无法计算得到目标t对应的聚类中心则按照下式更新目标t的后验状态估计和后验协方差矩阵

最后计算k+1时刻对目标t的先验状态来估计和协方差矩阵

以及测量触发标志变量ϕi(k+1)和通信触发标志变量ci(k+1),同时更新节点i以及邻居j的对目标t的最近一次通信触发的信息,即

ϕi(k+1)按照如下设计的事件触发测量策略进行计算:

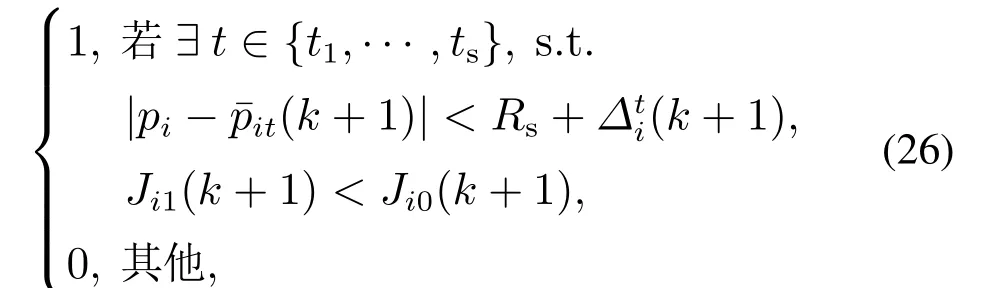
其中:pi∈代表节点i自身的位置,(k+1)∈是包含在状态估计(k+1|k)中的位置向量代表节点i对目标t的预测位置,

代表了对目标t位置的预测误差,[(k+1|k)]ll是(k+1|k)的第ll个对角线元素,P则是包含在状态向量中的位置变量的下标索引集合.Ji1(k+1)和Ji0(k+1)分别表示节点i是否触发测量的性能指标取值,具体定义如下:

ci(k+1)的更新则按照如下设计的基于事件触发的通信策略:

其中:

其中:

基于事件触发测量和通信策略的分布式多目标跟踪算法的具体实现流程如下所示:

1)系统参数设定和初始化:设定总的采样时间为T,采样时间间隔为∆T,通信半径为Rc,测量半径为Rs,η,β,初始化每个节点的位置以及每个节点的初始状态估计和协方差,设定触发测量标志ϕi(0)=1和触发通信标志ci(0)=1;

2)聚类:按照k-means聚类算法对节点i的接收测量值集合进行聚类预测目标t状态估计的类簇标签ccii(k),用聚类中心µt(k)作为目标t的测量值;

3)通信:在第k个采样时刻如果ci(k)=1,节点i发送信息给邻居j;如果邻居j触发通信的话,就接收邻居j的信息

4)信息融合:节点i接收邻居信息之后按照最小迹原则(12)–(14)进行融合得到和−1);

5)更新:用式(15)–(19)更新节点i对每个目标t的后验估计和协方差

6)预测:根据式(20)–(21)预测k+1时刻每个目标的先验估计和协方差用式(22)–(25)计算节点i及邻居j关于目标t最近一次通信的信息:

7)判断是否触发测量/通信:用式(26)–(30)分别计算节点i在k+1时刻对目标t的触发测量标志ϕi(k+1)及触发通信标志ci(k+1).

为了方便比较,同时实现了基于时间触发的多目标跟踪算法,具体实现流程如下所示:

1)系统参数设定和初始化:设定总的采样时间为T,采样时间间隔为∆T,通信半径为Rc,测量半径为Rs,初始化每个节点的位置以及每个节点的初始状态估计和协方差,设定触发测量标志ϕi(k)≡1和触发通信标志ci(k)≡1;

2)聚类:按照k-means聚类算法对节点i的接收测量值集合{,j∈,cj(k)=1}进行聚类预测目标t状态估计(k|k−1)的类簇标签ccii(k),用聚类中心µt(k)作为目标t的测量值;

3)通信:在第k个采样时刻,节点i发送信息

给邻居j;同时接收邻居j的信息

4)信息融合:节点i接收邻居信息之后按照最小迹原则(12)–(14)进行融合得到−1);

5)更新:用式(15)–(19)更新节点i对每个目标t的后验估计(k|k)和协方差(k|k);

6)预测:根据式(20)–(21)预测k+1时刻每个目标的先验估计k+1|k)和协方差(k+1|k).用式(22)–(25)计算节点i及邻居j关于目标t最近一次通信的信息:

注2式(26)中的事件触发测量机制主要是根据目标与传感器之间的预测距离来判断的.如果预测所有目标在传感器的测量范围之外,那么传感器就不触发测量,节省能量.式(30)中的事件触发通信机制由两部分因素决定.一方面,如果节点不触发通信,则由于没有新息一定不向邻居发送数据;另一方面,如果消耗的通信能量对应的指标大于对邻居估计协方差的减小量或者通信后协方差变化量相对不大,那么节点不触发通信.

3.2 算法分析

在本小节将对上述提出的基于事件触发测量和通信策略的多目标分布式估计算法的性能及稳定性做进一步地分析.针对上述多目标跟踪系统(1)–(2)定义目标t的拓展图由N个传感器节点和目标t(索引为N+1)组成.网络的感知拓扑

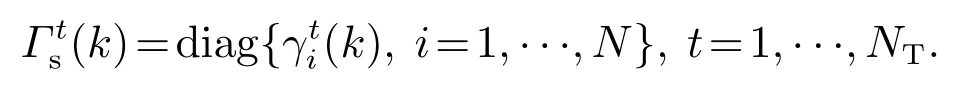
定义J(k)和(k)分别为k时刻所有节点基于事件触发测量和通信策略的多目标跟踪算法和基于时间触发的多目标跟踪算法的性能指标,那么

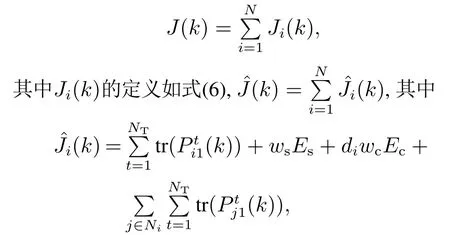
且ci(k)≡1,ϕi(k)≡1.

假设1监测区域内待跟踪目标的数目NT已知且固定.

假设2对于给定的时不变通信拓扑和时变感知拓扑(k),在每个采样时刻每个目标在拓展图中都是全局可达的.

定理1考虑具有离散线性动态方程(1)描述的多个目标和传感器网络(2)且满足假设1–2,假设每个节点测量值和目标轨迹之间对应关系已知.将基于事件触发测量和通信策略的分布式卡尔曼滤波算法应用到上述传感器网路的多目标跟踪(MTT)问题,那么基于事件触发的系统性能指标优于基于时间触发的性能指标

证因为每个节点测量值和目标轨迹之间的对应关系已知,网络估计中不存在聚类估计误差.下面分情况讨论的关系.

1)如果ϕi(k)=1且ci(k)=1,不难得到在其他节点的测量和通信状态都相同的情况下有下式成立:

2)如果ϕi(k)=1且ci(k)=0,那么

根据事件触发通信条件(30)可得∆e(k)wcEc,那么其中:

3)如果ϕi(k)=0,根据事件触发通信策略(30)可知ci(k)=0,那么

根据事件触发测量策略(26)可知Ji1(k)Ji0(k),因此

那么

假设3对于给定的时不变通信拓扑和时变感知拓扑,通信拓扑是连通的,在每个采样时刻存在节点对所有目标是协同可观的,即它和邻居的测量信息联合起来对所有目标可观.

定理2考虑具有离散线性动态方程(1)描述的多个目标和传感器网络(2)且满足假设1和假设3.将上述基于事件触发的分布式多目标跟踪算法中结合kmeans 聚类的事件触发分布式卡尔曼滤波算法应用到上述传感器网络的多目标跟踪(MTT)问题,那么在任意初始估计下,每个目标的估计误差在均方意义下有界.

根据假设3,令sk表示在k时刻对每个目标都协同可观的节点.定义的情况有

对于任意的j1∈Nsk,

其中2是Ft的最大奇异值.对于任意的j2∈Nj1,

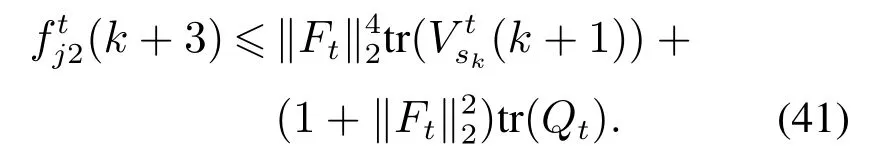
同样地,对于任意的jM∈NjM−1,其中M是图的直径

显然,对于任意节点i,

因此,如果存在一个节点的估计误差在均方意义下有界,那么其他节点的估计误差也将有界.

假设估计误差无界即在时刻k,充分大.当(k −1)充分大时,根据测量和通信触发机制得到对任意节点j,ϕj(k)=1,cj(k)=1.定义

那么存在一个小的常数α满足α<1使得

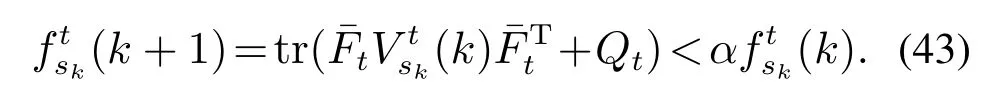
所以(k)不可能发散,从而(k)一定是有界的.综上,定理2得证. 证毕.

注3在文献[26]中仅考虑单目标的跟踪问题,设计事件触发的测量机制和分布式目标跟踪算法.本文考虑多个目标的跟踪问题,将事件触发机制拓展到事件触发测量和事件触发通信,并基于聚类算法和一致性卡尔曼滤波算法实现分布式多目标跟踪.

4 仿真实验

本节通过仿真例子对上述提出的基于事件触发测量和通信策略的多目标跟踪算法的有效性和收敛性进行验证.

考虑在监测区域运动的4个目标(NT=4),采样时间间隔设置为0.05 s,总的采样时间T=10 s.每个采样时间内传感器根据通信触发机制发送数据,与其邻居最多通信1次.离散化系统矩阵以及过程噪声协方差矩阵如下:

通信半径Rc为100 m,测量半径Rs为200 m,测量噪声每个目标的初始状态为

图1 节点分布和目标运动轨迹图Fig.1 Node distribution and target trajectory

图2 性能指标图Fig.2 Performance index

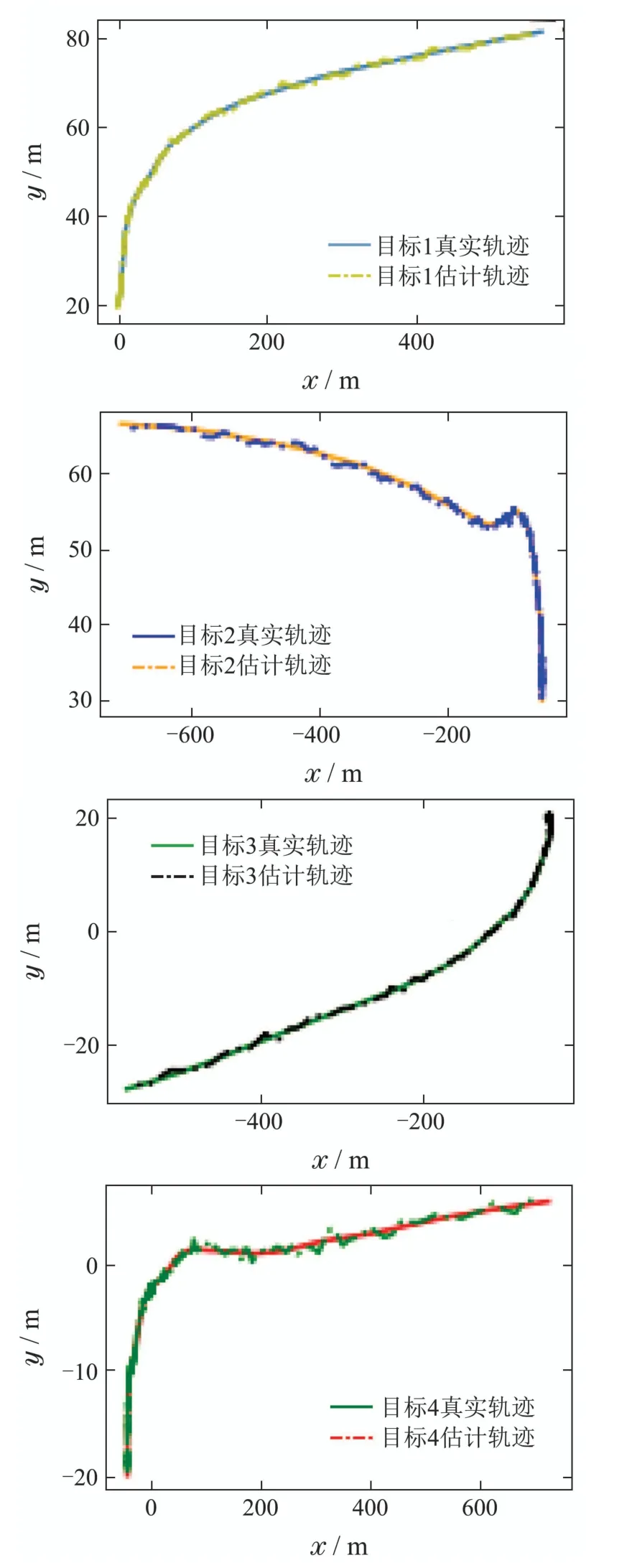
图3 目标估计轨迹图Fig.3 Estimated trajectory of target

图4 估计误差图Fig.4 Estimation error

图5 节点测量触发率图Fig.5 Node measuring-triggered rate

图6 节点通信触发率图Fig.6 Node communicating-triggered rate

图1绘制了监测区域内节点分布以及4个目标的真实运动轨迹,其中红色圆圈表示传感器节点,一共有112个.4个目标的运动轨迹分别如图中蓝色、黄色、绿色以及红色曲线所示.图2中两条曲线分别代表事件触发机制以及时间触发机制下系统性能指标随时间的变化.不难看出,每个目标都收敛到稳定值.图3是对应图4 中编号为59 的节点对4 个目标的估计轨迹以及目标的真实运动轨迹,而图4则是对应的估计误差曲线图.显然,该节点针对每个目标的估计误差都是有界的.图5是基于事件触发测量策略下节点的触发测量率,而图6 则是基于事件触发通信策略下节点的通信触发率.和全触发相比,节点的测量和通信率都有所下降,尤其是通信率的显著降低能够大大减少通信能量消耗.

5 本章小节

本文主要讨论当监测区域内存在多个目标时如何实现对每个目标实时有效的跟踪.针对多目标跟踪(MTT)亟待解决的数据关联问题,采用k-means聚类算法来解决传感器节点接收到的多个测量值和多个目标之间的对应关系.同时设计了基于事件触发测量和通信策略的分布式卡尔曼滤波算法实现跟踪误差和能量消耗之间更好的权衡.通过理论分析证明了事件驱动机制的优越性,并且当存在传感器节点对每个目标都协同可观时,每个传感器对每个目标的估计误差将在均方意义下有界.最后,给出了多目标跟踪的仿真例子来验证该算法的有效性和稳定性.