混合分布估计算法求解考虑同步性和准时性的三阶段装配集成调度问题

邓 超 胡 蓉 钱 斌

(1.昆明理工大学机电工程学院,云南昆明 650500;2.昆明理工大学信息工程与自动化学院,云南昆明 650500)

1 引言

装配制造业的生产过程包含从加工到装配形成最终产品的整个流程,将生产过程中各个阶段集成可有效地从整体层面进行资源配置,是装配制造业生产过程优化调度中非常重要的环节.因此,研究面向装配制造业的集成调度具有重要意义.目前,对装配制造企业车间集成调度研究主要针对含加工、装配的两阶段装配集成调度问题(two-stage assembly integrated scheduling problem,2sAISP)[1–2]和含加工、运输、装配的三阶段装配集成调度问题(three-stage assembly integrated scheduling problem,3sAISP).3sAISP在2sAISP的加工和装配阶段之间进一步增加运输阶段,但现有大量研究均假设运输阶段各工件的运输时间为常数[3–5],即运输车辆数量无限或载重无限,这与现实问题存在较大差距.因此,文献[6]进一步考虑运输车辆数量和车载重量有限会导致工件需按批量分别运输的实际情况,研究带工件批量运输的3sAISP.该问题研究极为有限且更符合实际,故对其及相关扩展问题开展研究具有重要的理论和实际意义.

同步性和准时性是企业物流中两个关键的因素[7].同步性可有效利用企业资源,建立与市场需求同步、连续的产品流.同步生产能够更好地满足生产中产品的多样性需求,有利于减少在制品库存[8].准时性是在客户需要的时间和地点,生产所需要数量和质量的产品和服务.装配制造业常将生产和交货整合在一起做出运营决策以提高准时性[9].大量文献把交货期(due date)作为衡量准时性的目标进行研究,使生产任务尽可能在各产品设定的交货期完成,从而提升客户满意度[10–12].然而,与准时性相比,同步性在现实生产中大都被忽略,结果导致生产资源浪费及成品(在制品)库存增加,同时也影响订单交付的准时性.因此,生产中考虑同步性具有重要现实意义.

目前,在生产调度中同步性的研究已开始得到重视.Li等[13]研究了不含加工阶段的装配–运输同步问题,以最小化供应链总成本为目标,建立整数线性规划模型求解问题.Zandieh等[14]研究了不含装配阶段的加工–运输同步问题,以最小化供应链总成本为目标,建立数学规划模型对问题进行求解.Tang等[15]研究了和文献[14]同样的问题,以最小化运营成本为目标,构建了数学规划模型,并根据问题性质提出了基于拉格朗日松弛分解的两层决策框架,最后用启发式方法和遗传算法对问题进行求解.Chen等[16]研究了不含运输阶段的加工–装配同步问题,以最小化生产同步性和交货准时性加权和为目标函数,构建了数学规划模型,并用改进的遗传算法对问题进行求解.通过以上文献调研可知,考虑加工–运输–装配三阶段的同步问题目前尚无人进行研究.然而,在实际生产过程中,加工–运输–装配同步性对产品生产连续性、在制品实际库存及交货准时性有很大影响.通过提升各阶段的同步性,可提高装配制造企业生产效率,增强企业市场竞争力.因此,本文研究以加工–运输–装配同步性和交货准时性加权和为优化目标的三阶段装配集成调度问题(3sAISP with synchronization and punctuality,3sAISP_SP)的建模与求解,具有较大工程意义.此外,在计算复杂度上,2sAISP已被证明为具有非确定多项式难(non-deterministic polynomial hard,NP−hard)的属性[1],该问题可归约为3sAISP,而3sAISP又可归约为3sAISP_SP,故3sAISP_SP亦为NP–hard.这表明研究3sAISP_SP也具有重要理论意义.

在已有文献中调度问题模型主要包括数学规划模型和排列模型.数学规划模型采用运筹学方法求解,譬如很多文献中采用基于分支定界、分支定价等方法的商用求解器GUROBI 或CPLEX求解.由于这些运筹学方法遍历或部分遍历解空间,故较短时间内(即几分钟内)只能求解小规模问题.排列模型一般采用智能优化方法求解.排列模型将问题解空间压缩为一个极度扁平的空间,使得优化目标函数值的范围远小于问题解或排列的数量,大量不同解对应相同目标函数值.同时,智能优化算法是在带保优的随机搜索基础上加入特定的进化寻优机制.这使得智能优化算法在短时间内只搜索排列模型解空间的很小区域,却能在目标函数值上搜索到明显多于运筹学方法的较好区域,从而可有效求解不同规模问题.这是智能优化调度算法近年快速发展的主要原因.因此,本文设计智能优化算法求解不同规模的3sAISP_SP(对应排列模型),同时采用基于运筹学方法的GUROBI 获取小规模3sAISP_SP(对应数学规划模型)的最优解,以验证所提算法的近似最优性.

分布估计算法(estimation of distribution algorithm,EDA)是一种基于统计学的新兴进化算法,以统计的方式对种群中的优质个体进行学习并构造概率模型,然后对概率模型进行采样产生新种群,从而引导算法的搜索方向,具有较好的全局搜索能力.EDA在生产调度领域已开展较多研究.李子辉等[17]考虑3sAISP问题,以平均完成时间和延迟时间加权和为优化目标,提出一种自适应EDA求解.该算法通过设计基于信息熵的概率分布模型自适应更新机制和保留优良模式的新种群采样生成方法来增强全局搜索能力,同时提出基于插入(insert)操作的邻域搜索来增强算法的局部搜索能力.Qian等[18]考虑可重入流水线调度问题,以最小化最大完工时间(makespan)为优化目标,提出基于COPULA函数的EDA求解.该算法利用各变量的边缘分布和COPULA函数构造变量联合分布概率模型,同时提出基于关键路径的块结构性质,并基于该性质构造局部搜索.Wang等[19]考虑柔性制造系统的调度问题,以makespan为优化目标,提出了一种混合EDA求解.该算法提出变量邻域搜索的方式产生后代个体,从而在其邻域中获得更好的解以提高算法性能.Li等[20]考虑带序相关设置时间的多目标作业车间调度问题,以makespan和总设置费用为优化目标,提出遗传算法和EDA融合的算法求解.该算法构建新颖的双种群协同进化框架,有利于引导搜索发现优质解区域.虽然EDA已在多种生产调度问题上取得成功应用,但针对3sAISP_SP的研究处于空白状态.

本文研究以生产–运输–装配同步性和交货准时性的加权和为优化目标的三阶段装配集成调度问题(3sAISP_SP),并基于问题特点设计混合分布估计算法(hybrid estimation of distribution algorithm,HEDA)进行求解.首先,分别建立3sAISP_SP的数学规划模型和排列模型.其次,在对问题模型特点分析的基础上,提出求解3sAISP_SP 的HEDA.在HEDA中,设计合理的编码和解码规则,同时利用基于概率模型的全局搜索以发现问题解空间存在优质解的区域.为进一步提高算法性能,设计3种局部搜索策略对优质解区域进行细致搜索.然后,在小规模问题下,将HEDA得到的较优解与GUROBI得到的最优解进行比较,验证HEDA的求解结果接近最优解;在较大规模问题下,将HEDA与其他有效智能优化算法进行比较,验证HEDA的求解性能.最后,讨论装配同步性和交货准时性的合理权重组合及装配同步性对半成品库存的影响.

2 问题数学模型

2.1 问题总体描述

设产品集为P,z∈P,P={1,2,…,HP};车辆集为T,t∈T,T={1,2,…,HTR};零件集为Q,零件总数为q,j∈Q,Q={1,2,…,q},组成第z个产品的工件数为Pz;工序集为O,工序总数为HO,i∈O,O={1,2,…,HO};加工阶段设备集为M.加工阶段设备数为m1台,M={1,2,…,m1},装配阶段组装设备数为1.每种产品由多个工件组成,每个工件的不同工序需要按先后顺序在加工阶段m1台满足加工约束的设备上加工,完成加工后由运输阶段HTR辆车在车载额定载重VT限制条件下运输到装配阶段等待组装.车辆可来回w趟,其中w1.t-tran为车辆t的运输时间.各产品对应的工件按加工顺序依次经过3个阶段进行处理;加工阶段的任一加工设备在同一时刻只能加工一种工件,不同零件带释放时间;装配阶段的组装设备在同一时刻只能组装同一种产品,不同产品间设置时间为零.

完成的每个产品都有其单独的交货截止日期Dz,任何早于或晚于Dz完成的产品将受到提前或迟到的处罚.此外,受车辆额定载荷及运输效率限制,工件在加工阶段完工之后并非立刻被车辆运输走,若不够装满一辆车或者需要等待车辆往返运输,完工工件需要放入中转区域等待,从而产生了完工工件库存.由此可见,在满足装配同步性和运输准时性的同时使产品在恰当的时间完成生产以满足交货期.3sAISP_SP模型图如图1所示.

图1 3sAISP_SP模型图Fig.1 The model of 3sAISP_SP

2.2 优化目标加权和函数

以同步性为目标的生产调度问题通常运用工件完成时间与基准之间的平均差异来衡量[21].然而,平均差异衡量方法在某些情形下容易发生补偿效应而不能客观反映同步性.因此,本文选用最长装配等待时间WT来衡量同步性,即属于同一产品的工件最早到达装配中心时间与最晚到达装配中心时间之间的间隔,并提出平均最长等待时间指标fs来衡量装配同步性,即

以满足准时性为目标的调度问题通常以基于时间和基于成本的这两种指标来衡量.基于成本的方式是通过乘以惩罚系数得出提前或迟到时间的惩罚成本,但受到一些隐含的因素影响较难准确确定惩罚系数[22].因此,本文采用平均提前和迟到时间作为交货准时性目标函数fp,即其中CA表示产品的三阶段总完工时间.

将两个目标通过一定的权重合并成为单个目标,即f=ωsfs+ωpfp.其中,同步性的权重为ωs,准时性的权重为ωp,且ωs+ωp=1.

2.3 问题模型

2.3.1 3sAISP_SP数学规划模型

1)关于本节所涉及的数学符号及定义如下:

参数:

Qj:工件j的工序总数;

Oi,j:工件j的第i个工序;

Mij:对Oi,j可加工的机器;

tw:车辆t来回运输的趟数;

A:一个很大的数;

Pijk:Oi,j在机器k上的加工时间;

Rjk:工件j首次到达第k台加工设备的时间,即释放时间;

Vj:工件j的载荷;

Az:产品z的装配时间.

中间变量:

SPijk:Oi,j在机器k上的开始加工时间;

CPij:Oi,j的完工时间;

CPj:工件j在加工阶段的完工时间;

STjtw:工件j在车辆t第w趟的开始运输时间;

STtw:车辆t第w趟的开始运输时间;

CTtw:车辆t第w趟的结束运输时间;

CTj:工件j的结束运输时间;

SAz:产品z开始装配时间;

CAz:产品z装配完工时间.

布尔变量:

2)数学规划模型:

式(1)为目标函数;约束(2)−(6)为工件首次加工有释放时间;约束(7)为工件的前一操作完成后才能进行后一个操作;约束(8)为工件在机器上的完工时间;约束(9)为工件的每个操作可从可选加工机器集中选出一台机器进行加工;约束(10)−(11)为每台可加工机器在同一时间只能进行一次操作;约束(12)为工件加工阶段完工时间;约束(14)−(15)为每个工件只能被车辆运送一次;约束(16)为装入每辆车的工件总载荷不超过车辆额定载荷;约束(17)−(18)为工件按工件序列分配给运输车辆且只分配一次;约束(19)为工件开始运输时间;约束(20)为工件完工运输时间受装入该车辆中工件的完工时间限制;约束(21)为工件开始运输时间受装入该车辆前一趟运输开始时间限制;约束(22)为运输结束时间;约束(23)−(24)为产品按顺序依次安排到装配机器上进行装配;约束(25)为属于同一产品的所有工件到达后才能进行装配;约束(26)为装配机器在同一时间只能装配一个产品.

2.3.2 3sAISP_SP排列模型

1)加工阶段:带释放时间的多工序异构并行机调度问题(HPMP_RT).为所有工件的工序在加工阶段的排列.加工设备k上加工工序的数量为Hk,πk=为工件的工序在加工阶段加工设备k上的排列,为πk中第i个位置的工件的工序.的加工时间,为πk中第i个位置的工件首次到达第k台加工设备的时间,即释放时间.前一次加工工序的设备号,前一个工序在设备号为上的排列表示为若工件首次加工,则在第k台机器上加工时该台机器上前一次加工的工件工序,工件工序在排列中的位置记为若加工的机器为首次加工工件,则的完成时间计算如下:

2)运输阶段:带车辆载重约束的多车辆单点配送问题.wt为表示车辆t来回运输的趟数,wt1.Vt为车辆t的额定载荷(定值).t_tran为表示车辆的运输时间(定值).为所有工件在运输阶段的排列,为πTR中第j个位置的工件.为πTR中第j个位置的工件加工阶段的完工时间.为πTR中第j个位置的工件的重量.为πTR中第j个位置的工件在第t台车辆的开始运输时间.为运输阶段第wt趟装载在车辆t里πTR中第j个位置的工件的完工时间,πTR中第j个位置的工件在运输阶段的运输完成时间计算如下:

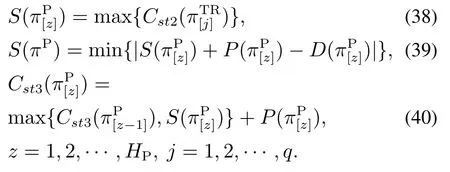
4)优化目标.优化目标为在所有产品所组成的工件从加工、运输到装配三阶段顺序的集合Π中找到一个最优排序π∗=(πK,πTR,πP),使得准时性fp与同步性fs的加权和f最小.其中:为产品的交货截止日期;为产品的交货截止日期与实际完成时间的差值;为属于同一产品的工件最早到达装配中心时间与最迟到达装配中心时间之间的间隔.

2.3.3 两类模型的特点

与绝大部分组合优化问题一样,3sAISP_SP的常用模型包括数学规划模型和排列模型.由于该问题为NP−hard问题,不存在获取最优解的多项式时间算法.

从第2.3.1节可知,3sAISP_SP 的数学规划模型由目标函数(即式(1))和一系列显式不等式和等式约束(即式(2)至式(29))组成,属于0−1混合整数规划问题,具有非凸特性.该类模型主要采用运筹学方法求解.数学规划模型包含大量不等式或等式约束.譬如,对于50个工件、5道工序、5台机器的中等规模问题,仅式(6)就含近1250个不等式约束.这些约束式可较全面刻画问题结构,但其庞大的数量明显增加了算法确定可行解区域和在该区域发现最优解或近似最优解的难度,使得算法求解质量取决于具体问题的复杂度以及算法设计者对该问题结构(特别是几何结构)的理解程度.对于中大规模问题,算法(如分支定界法、分支切割法)要在较短时间获取问题满意解的难度大.

从第2.3.2节可知,该问题的排列模型(即式(30)至式(47))由各工序加工完工时间、工件运输完成时间、产品装配完成时间的计算公式组成,约束隐式包含在这些公式和解的编码、解码(见第3.2.1节)中.该类模型多采用智能优化算法求解.排列模型的约束不显式出现,容易设计有效的编码、解码和搜索操作来避免违反约束,使得算法搜索集中在可行解区域进行.同时,该类模型把问题解空间压缩为一个极为扁平、紧凑的空间,其目标值变化范围远小于解空间规模,大量不同的解具有相同目标值.因此,采用排序模型可使算法仅需搜索解空间中极小可行区域就能覆盖目标值较大区域,有利于算法快速获取较大规模问题的满意解.

综上,为使算法能对不同规模的3sAISP_SP进行有效求解,本文采用问题的排列模型,并设计智能优化算法HEDA求解.

2.4 问题示例

本节通过一个例子来说明3sAISP_SP.考虑一个三阶段装配集成调度问题,第1阶段为3台异构并行机,第2阶段为2辆具有相同载重的运输车辆,第3阶段为1台装配机器,需要加工装配完成3个产品.产品构成如图2所示,3个产品由多个工件装配而成,每个工件具有多个工序,每个工序可在多台机器上加工.产品各阶段数据见表1,车辆运输时间为t_tran=200,权重为ωs=ωp=0.5.该示例形成的甘特图如图3所示.

在图3中:V1−1表示第1辆运输车辆的第1趟.该车辆在满足载荷的前提下运送属于P1,P2产品的J5,J1,J4三个工件,且CT51=CT11=CT41=614;V2−1车辆运送属于P1,P3产品的J2,J3,J9工件,CT22=CT32=CT92=692,属于P1的工件全部到达开始装配,则WT1=692−614=78.此时两辆运输车辆均已在途,剩余加工完的工件需要等待车辆往返方能被运送,故V1−2车辆运送属于P2,P3产品的J8,J7,J6三个工件,CT81=CT71=CT61=1014,则

图2 示例产品构成Fig.2 An example of products composition

表1 产品各阶段数据Table 1 Data of each stage of the product

图3 3sAISP_SP的甘特图Fig.3 A Gantt chart of 3sAISP_SP

3 求解3sAISP_SP的HEDA算法设计

3.1 3sAISP_SP的特点分析

1)整体性和系统性.3sAISP_SP并非为3个阶段子问题的简单叠加(见图3),前一个阶段的调度结果直接影响后一个阶段的优化.因此,设计求解算法时应从整体优化出发.

2)优化目标与各阶段之间的联系.优化目标中的同步性和准时性均用时间来度量.同步性贯穿于各个阶段并影响准时性,前一阶段同步性是后一阶段同步性的基础;准时性由装配阶段产品完工时间最终确定.

3)问题解空间复杂.3sAISP_SP是多阶段耦合的调度问题,其问题解空间非常复杂,故需分析和利用问题特点来合理缩小搜索空间.

结合1)和2)的分析提出以下3条规则:

规则1属于同一产品的工件在加工阶段分配相同的优先级有利于提高同步性.

规则2属于同一产品的工件在满足车辆装载约束下尽量放入同一辆车有利于提高同步性.

规则3交货期越早的产品尽早装配以提高交货的准时性.

通过3)的分析可知,设计算法时要尽量减小搜索范围,以提高搜索效率,同时需合理构造搜索操作,以实现对复杂解空间的有效搜索.

综上,为提高算法求解3sAISP_SP的效率,本文的HEDA不采用常规对整个问题的编码和解码,而采用分阶段的编码和解码,并在此基础上只对加工阶段执行基于智能优化的搜索以确定对应子问题的解,而对运输和装配阶段采用结合规则的解码直接确定对应子问题的解.

3.2 求解3sAISP_SP的HEDA算法设计

本文设计的HEDA只对加工阶段的子问题(即带释放时间的多工序异构并行机调度问题)解空间进行搜索,在此基础上在运输和装配阶段依据问题性质设计相关策略得出优化目标函数值.具体来说,HEDA求解3sAISP_SP包含以下环节:1)根据加工阶段的编码生成相应的种群,然后利用所设计的算法操作来执行进化并实现搜索;2)在计算个体或解对应的优化目标值时,首先根据解中工件具体排列,利用加工阶段的解码计算各工件完工时间;然后设计相关操作分别对运输及装配阶段进行编码和解码;最后依据相应权重获得整个问题的优化目标值.

3.2.1 编码及解码

1)加工阶段编码及解码.

编码:第1部分为加工阶段基于工序的排列,其长度是由产品层−工件层−工序层确定,即产品对应工件集合Pz及工件对应工序集合Qzj确定,z∈P,j∈Q.如第2.4节示例所示Pz={3,3,3}表示有3个产品,每个产品都由3个工件组成,总工件数为3+3+3=9,表示产品P1对应3个工件的工序数为[2,1,3],产品P2对应3个工件的工序数为[3,3,3],产品P3对应3个工件的工序数为[2,3,2],第1段编码可表示为{1,7,4,6,8,9,4,5,2,8,9,3,6,5,3,7,5,3,4,6,1,8}.

解码:加工阶段是三阶段的开始也是核心,解的质量直接影响后两个阶段.因此,本文设计最早完工时间(earliest completion time,ECT)规则[17]与插空相结合的形式进行解码,确定各个工序的开始加工时间并完成机器分配.

2)运输阶段编码及解码.

编码:第2段编码为运输阶段基于工件的排序,按照工件在加工阶段完工时间非降序得到对应编码πTR.如工件在加工阶段完工时间分别为

则工件排序为{6,3,1,9,8,2,4,5,7}(见图4).

图4 编码方式Fig.4 Encoding

解码:πPD为产品按交货期非降序得到的排列,为πPD中第z个位置的产品;V[t]为第t辆车当前载重.根据规则2−3对运输阶段进行解码,具体步骤如下:

Step 1从工件排列πTR中从左到右依次选出属于产品的工件

Step 2将选出的工件在满足VT的条件下依次装入车辆t,当满足>VT则将工件j放入车辆t+1中,并更新和待运输工件集合,转入Step 3.

Step 3检验待运输工件集合中是否存在工件满足若满足则将工件放入车辆t中,更新V[t],直至更新待运输工件集合,t=t+1,z=z+1.

Step 4转入Step 1,直至待运输工件集合为空.

3)装配阶段编码及解码.

编码:第3段编码为装配阶段基于产品的排序,按照组成产品所有工件中最晚到达装配阶段的时间非降序排列得到对应产品编码πP.如组成产品P1,P2,P3最后一个工件到达装配车间的时间分别为21,34,17,则产品排序为{3,1,2}(见图4).

解码:考虑到交货准时性,按照最小交货时间优先规则进行解码,从而确定各产品完工时间.

3.2.2 权重的设置

如果决策者依据偏好给出权重组合,则将问题搜索方向固定在一维目标空间中.如果没有给出权重偏好,则将对权重进行调整以确定最佳权重组合.本文采用一种线性调整权重方式来实现[16].n为运行的总次数,为当前运行数,1nF;ωs(n),ωp(n)分别为当前运行数下的权重,则ωs(n)=(n−1)/F,ωp(n)=1−ωs(n),0ωs(n)1.权重变化频率通过F调整,但F不能太高,这样会消耗太多的计算时间.因此,在第5节中运行10次以获得最佳权重权衡是相对合理的.

4 HEDA求解3sAISP_SP

4.1 HEDA全局搜索

4.1.1 初始化种群及概率模型

根据规则1,令种群规模为popsize,本文设计按产品聚合(product aggregation,PA)的方式产生η×popsize个体,剩余个体随机产生来初始化种群.PA规则为先随机生成产品序列,以产品为基础随机生成组成该产品的工件序列,再对应工件的工序,随机生成工件基于工序的排列作为初始化种群.

种群随机产生的过程具体如图5所示(示例第2.4节).按照PA规则可使组成产品的工件较为集中,加工阶段集中加工完后,能较快的较为集中被运输到装配阶段,从而缩小了中间库存,提高装配同步性.

图5 按PA规则随机生成初始种群Fig.5 Randomly generate initial population according to PA rules

根据第3.2.1节的编码方式采用加工阶段基于工序排列矩阵ρ作为概率模型ρi,j.为尽可能保证算法对解空间均匀搜索,概率模型采用均匀分布,即ρi,j(0)=

4.1.2 概率矩阵更新

在每次迭代中选取种群中φ%的优质个体更新概率模型.Ii,j表示统计工件j出现在工序排列向量第i位上或是之前的次数.Ei,j(g)表示第g次迭代中通过优质解统计出来得到的概率.由此可通过更新ρi,j(g),其中γ∈(0,1)为学习速率.

4.1.3 采样方式

算法在后续的每次迭代中,新种群通过采样概率矩阵生成.采样方式是根据问题性质1而设计的,目的是使属于同一个产品的工件有更大的概率聚合在一起,产生较为优质的个体,但每次的采样均选用轮盘赌操作,在一定程度上保证了种群的多样性.一旦产生新个体便构成了下一次迭代的新种群.

4.2 局部搜索策略

通过概率矩阵采样出种群新个体后用优质个体来更新概率矩阵,为了更好引导全局搜索方向,本节结合规则1,设计3种情形下的局部搜索策略,有利于避免一些无效搜索,在提高解的质量的同时能够较好的保留原有解的结构.

从选择的φ%×popsize优质个体组成集合ψ={π1,π2,π3,…,πm},对ψ中个体πr,其中r=1,2,…,m随机选取两个位置u,v(uv),πr(u)表示个体πr第u个位置的工件编码.

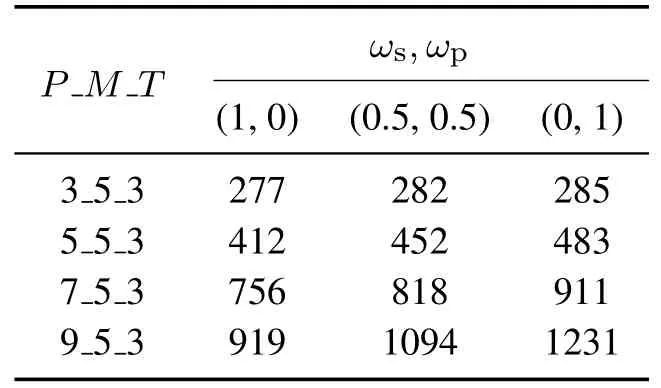
情形1若πr(u)=πr(v),表明这两个位置上为同一工件,swap操作将无效,此时进行insert操作.若u

情形2若πr(u)πr(v),表明这两个位置上为不同工件,若属于同一产品,进行一种基于insert和swap变邻域局部搜索混合操作.具体步骤如下:

情形3若且不属于同一产品,令x=max(u,v)−min(u,v),表 示所有产品的工序总数,即个体πr的加工阶段的长度,HP为产品总数),若满足xk,则进行Swap操作,生成新个体

4.3 种群多样性判定及控制机制

随着算法的不断迭代,种群多样性会降低,种群中的个体变得非常相似,这样会导致算法陷入局部最优.为了解决这个问题,本文采用文献[23]方法计算当代种群的多样性值θdiv.给定一个多样性阈值δ,当满足θdivδ时,对当前种群进行调整,保留当代种群中前φ×popsize/3个优质个体,用PA规则随机生产φ×popsize/3个个体,剩下随机产生.

4.4 HEDA

由第4节可知,HEDA在算法操作层面,不仅采用概率模型学习优质解信息并引导算法全局搜索,同时利用第3.1节对问题分析得到的规则,设计3种情形下基于邻域操作的局部搜索,对全局搜索发现的优质区域进行细致搜索,从而使算法在全局和局部搜索之间达到良好平衡,可实现对复杂解空间的有效搜索.HEDA的算法框架如图6所示.

5 仿真实验结果与分析

本节分为3部分:第1部分依据第2节构建的数学规划模型与排列模型,对小规模问题分别用优化求解器GUROBI与HEDA进行求解,以验证HEDA求解结果的近似最优性,同时对较大规模问题用HEDA和其他有效智能算法求解,以验证HEDA的求解性能;第2部分研究了在两个指标下,同步性与准时性的权重设置问题;第3部分讨论了同步性对半成品库存的影响.

5.1 HEDA算法比较

所有的测试问题都是基于三阶段装配集成系统的结构设计的,测试数据请具体参见(https://pan.baidu.com/s/1Vsd4xBpBE50TbyF6w78fHg).3sAISP_SP 每个产品所组成的工件数及工件所对应工序数在[2,5]和[1,3]随机生成,各工件工序加工时间及每个产品的装配时间在[20,80]和[100,200]随机生成,每个工件的载荷在[20,50]随机生成,每个产品的交货期由最大平均完工时间的[50%,100%]均匀分布产生.运输车辆数对每个测试问题有不同的影响,本文列举的测试问题表达为P_M_T.所有算法和测试程序均用Delphi 2010编程实现,操作系统为WinXP.所有算法在相同的测试时间下独立运行10次.

图6 HEDA算法框架Fig.6 The algorithm framework of HEDA

5.1.1 小规 模 问题 下GUROBI与HEDA算法 实验结果比较

本文用优化求解器GUROBI求解第2.3.1节中的数学规划模型,同时用HEDA求解第2.3.2节中的排列模型.表2为权重ωs=ωp=0.5,在小规模问题下分别采用GUROBI和HEDA求解结果比较.表中第1列表示工件数J,第2列P_M _T为对应问题规模,随后两列表示GUROBI求得对应问题规模的最优解(optimal solution,OPS)和时间,其余列分别表示HEDA对测试问题分别进行10次独立实验的最好值Best、平均值AVG、平均相对偏差值RPDs、平均绝对偏差值MADs和运行时间.从表中数据可知RPDs均值和MADs均值相对较低,且求解时间明显低于GUROBI,这说明所提算法获得的解非常接近问题的最优解,具有良好的近似最优性.

表2 GUROBI和HEDA比较(ωs=ωp=0.5)Table 2 Comparison of GUROBI and HEDA(ωs=ωp=0.5)

5.1.2 HEDA与其他智能算法实验结果比较

为了进一步验证HEDA的性能,本节针对17个中大规模问题,将HEDA与近年国际期刊中的有效算法GA[2]进行对比.其中:HEDA 的参数设置为:popsize=120,η=0.6,γ=0.15,φ=0.3;GA[2]的参数设置为:popsize=150,pc=0.3,pm=0.6.两种算法所选择的参数均为参数实验后得到的最好参数.HEDA运行200代,GA运行时间与HEDA相同,两种算法的对比结果如表3所示,测试指标包括最好值Best、最差值Worst、平均值AVG、方差SD.从表3中可以看出,HEDA在大多数问题上优于GA,且SD值占优,这表明HEDA可有效求解3sAISPSP问题.

表3 HEDA与GA[2]比较(ωs=ωp=0.5)Table 3 Comparison of HEDA and GA[2](ωs=ωp=0.5)

5.2 权重设置对同步性和准时性的影响分析

在实际生产过程中企业的资源是有限,即加工机器和运输车辆一定,针对在不同产品数(订单)情况下,进一步研究不同权重组合对同步性和准时性的影响,为企业决策者提供较好的参考.

本节考虑加工阶段有5台异构并行机,3辆运输车辆,产品数选取3,5,7,9,用本文第3.2.2节权重取值方法,令F=10确定11种权重组合ωs,ωp,求得在HEDA下同步性FS(fs)、准时性FP(fp)两个指标的数据(见表4).

表4 权重设置实验结果Table 4 Results of weight trade-off

为了直观地比较FS,FP不同规模下不同权重组合的变化趋势,对表4的结果进行归一化处理,FS,FP在不同规模下的结果见图7−8.由图可知,FS,FP在不同规模下的结果见图7−8.由图可知,FS随ωs减少而增加,FP随ωp减少而增加,说明在WSM目标函数中考虑同步性及准时性可以给生产带来显著改善.从权重组合(0.5,0.5)到(0,1),FS,FP斜率变化都变缓.尽管针对不同的测试问题有不同优先权重组合,但在(0.5,0.5)到(0,1),之间FS,FP达到了相对平衡,差异度最小.因此,对决策者来应优先从(0.5,0.5)到(0,1)范围内选择权重组合较为合理.

图7 FS数值Fig.7 The value of FS

图8 FP数值Fig.8 The value of FP

5.3 同步性对半成品库存的影响

库存是企业非常重要的要素之一.工件从加工阶段完工后受到运输车辆的装载限制不能马上被运输走,需要对工件进行暂时存储称为半成品库存(semi-finished inventory,SI).本节将比较在上节4种问题规模下的权重组合为(1,0),(0,1)及优先权重组合(0.5,0.5)3种情况下的SI.其中,CPj).每个情况在不同规模下进行10次独立实验.每个规模均取优先权重组合运行100代,而在其他权重组合的运行时间与其相同.

具体结果如表5所示.

表5 3种权重组合下SI数据比较Table 5 Comparison of SI data with three weight combinations

从表中数据可知,权重组合为(1,0)和(0.5,0.5)都优于(0,1).这表明侧重考虑同步性这一目标可有效地降低SI水平.此外,还可看出权重组合为(1,0)的SI值小于(0.5,0.5),这是由于(1,0)的权重更大.但这一结果并不影响决策者对优先权重的选择,若半成品库存较大超过可接受的范围,可多派运输车辆等策略以降低SI水平.

6 结语

本文针对以加工–运输–装配同步性和交货准时性加权和为目标的三阶段装配集成调度问题研究相应的问题建模、求解算法和目标权重设置.在建模方面,建立问题的数学规划模型和排列模型,并阐述两类模型的联系和区别,指出排列模型结构简单、约束隐式包含在解的编码中,适合设计智能优化算法求解.在求解算法方面,结合问题特点设计合理的编码和解码规则,利用EDA概率模型学习优质解信息并引导算法全局搜索,以发现解空间中存在优质解的区域,同时基于多种邻域操作设计局部搜索对优质解区域进行深入搜索,以增强算法的局部搜索能力,进而提出混合分布估计算法(HEDA).通过在不同规模问题上的仿真实验和算法比较,验证HEDA可有效求解3sAISP_SP.在目标权重设置方面,进一步分析同步性和准时性的合理权重组合及同步性对半成品库存的影响,并得到以下几个结论:1)考虑同步性对减少半成品库存起着重要作用;2)不能一味的追求准时性,可能会严重影响同步性;3)决策者可优先从(0.5,0.5)到(0,1)范围内选择权重组合以达到两目标间的较好平衡.下一步的研究将在此模型基础上进一步考虑装配–配送同步问题,并提出更加有效的算法进行求解.