基于三步法的机械臂轨迹跟踪控制

于树友 孟凌宇 许 芳 曲 婷陈 虹

(1.吉林大学汽车仿真与控制国家重点实验室,吉林长春 130022;2.吉林大学控制科学与工程系,吉林长春 130022;3.同济大学新能源汽车工程中心,上海 200092)

1 引言

机械臂在工业生产过程中起着十分重要的作用,它可以代替人类在复杂、恶劣的环境下工作[1–2].机械臂是一个多输入多输出的、具有时变和强耦合特性的非线性系统.高精度的轨迹跟踪控制是工业机械臂大规模应用的基础.文献[3–5]基于改进的PID或PD控制方法设计机械臂的轨迹跟踪控制器,但设计实现起来复杂繁琐.文献[6–7]提出了基于PD的逆动力学控制,将机械臂非线性模型解耦,通过将线性位置和速度跟踪误差替换为指数型误差来实现对机械臂系统的控制,并利用李雅普诺夫直接法证明了系统的全局有限时间稳定性.文献[8]提出了一个受驱动器约束的、饱和PID控制器,该控制器可以全局渐近调节机器人的运动,并且能够消除执行器由于输入转矩过大而失效的可能性.针对具有不确定性和扰动的机器人的轨迹跟踪控制问题,文献[9–10]设计了模糊滑模控制器,在严重参数变化和干扰的情况下,从提高跟踪性能的角度证明了该方法相对于传统滑模控制的优越性,但没有解决滑模控制的抖振问题.文献[11]设计了滑模控制器与神经网络自适应观测器,在保证机器人能够跟踪上理想轨迹的基础上减小了滑模的抖振.文献[12]提出了一种基于自适应反演非奇异快速末端滑模控制的机器人跟踪控制方法处理机械臂的扰动和不确定性,该控制器的瞬态响应快,跟踪误差小,抖动小.文献[13]设计了两个滑模控制器,分别用来补偿不确定运动学和动力学的影响,保证控制精度.文献[14]利用自适应雅克比矩阵估计了未知运动学参数,采用了3层神经网络对动力学和未建模项动态进行补偿.文献[15]提出了一种基于状态空间模型的约束预测控制方法,并结合前馈–反馈控制结构抑制输出端扰动,在仿真实验中,该算法体现了良好的控制性能以及抗扰动能力.文献[16]提出了一种径向基函数(radial-basis function,RBF)神经网络控制器逼近机械臂中的不确定项,并采用遗传算法优化出最佳的网络权值,减少了控制器的计算时间,并且提高了系统的性能.针对重力对机械臂的影响,文献[17]提出一种自适应鲁棒控制器对重力加速度进行在线估计,并通过鲁棒控制器对系统的不确定性进行了补偿;文献[18]在文献[17]基础上考虑了外部扰动,设计了一个自抗扰控制器并与PD控制器进行了对比,证明该算法不仅可以抵抗扰动还具有很强的鲁棒性.

轨迹跟踪广泛应用于机械臂的控制,也是机械臂控制的基本控制问题.目前广泛存在的PID控制器高度依赖参数整定并且无法适用于系统所有工况;计算力矩法依赖系统精确的动力学模型;自适应控制器要求辅助系统状态必须在约束子集中初始化,否则无法实现全局跟踪;滑模控制器存在的抖振问题会导致机械臂的磨损,去抖振控制器设计复杂并会延长控制时间.这些都要求考虑设计参数整定简单、对系统中存在的不确定性鲁棒、不依赖于系统精确数学模型、控制量变化平稳且速度快的控制方法.

三步法控制是从现代汽车工程中提炼出来的一种基于模型的控制方法,主要解决跟踪控制问题.目前主要应用于单输入单输出系统以及反馈控制动态之间相互独立或是解耦的两输入两输出非线性系统的控制[19–21],该方法采用了“前馈–反馈”的控制结构,具有很强的鲁棒性.本文将三步法控制器扩展到状态相互耦合的(三输入三输出)3自由度机械臂动力学系统,并且证明了机械臂末端轨迹可以渐近收敛到期望轨迹.在3自由度机械臂上进行了仿真实验验证设计的轨迹跟踪控制器的有效性.

本文第2节介绍3自由度机械臂的动力学模型和正、逆运动学方程,同时描述系统的控制问题.第3节完成了三输入三输出的机械臂三步法控制器的设计.第4节通过仿真验证了该控制器的有效性.第5节对本文进行总结.

2 问题描述与系统建模

3自由度机械臂模型如图1所示.

图1 3自由度机械臂模型Fig.1 3−DOF manipulator model

根据拉格朗日功能平衡法[22],建立其动力学模型.为了建模方便,忽略了未建模项以及外界扰动,只考虑了摩擦项(忽略了手腕的部分,只考虑底座,第1个连杆和第2个连杆).以底座与前臂的转轴处为原点,建立如图所示基础坐标系.其中:第1个连杆的长度为l2,质量为m2;第2个连杆的长度为l3,质量为m3;r2为第1个连杆的质心距离关节2的距离,r3为第2个连杆的质心距离关节3的距离.机械臂动力学模型如下所示:

u为每一个关节的驱动力矩u=(τ1τ2τ3)T.

根据空间几何法,建立3自由度机械臂运动学方程如下:

其中(x,y,z)为机械臂末端位置.

对于已知末端轨迹,本文采用代数法对机械臂的逆运动学求解[24],可得到4组逆解:

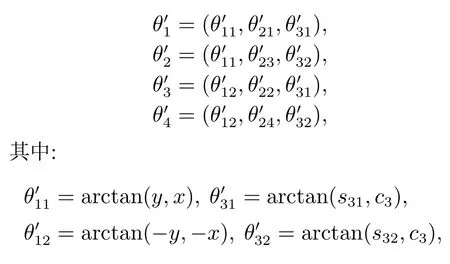
由于机械臂是一个渐变系统,本文选取与上一时刻机械臂3个关节角度误差绝对值之和最小作为逆运动学的解,并且把它作为当前时刻机械臂的参考关节角度.

机械臂的轨迹跟踪问题可以描述为:给定一个参考轨迹,找到一个容许控制u=(τ1τ2τ3)T,使得实际的关节角度与参考的关节角度误差最小,从而使得机械臂末端轨迹跟踪上参考轨迹.

3 三步法控制器设计

基于文献[25]所提出的三步法非线性控制策略,设计了一种机械臂轨迹跟踪控制器.本文采用了2阶三步法,并应用于控制量存在耦合的三输入三输出仿射非线性系统.三步法控制器由3部分组成、依次分3步推导,控制器推导的思路简单明了、结构层次清晰.

首先将机械臂仿射非线性系统写为如下标准形式:

其中:

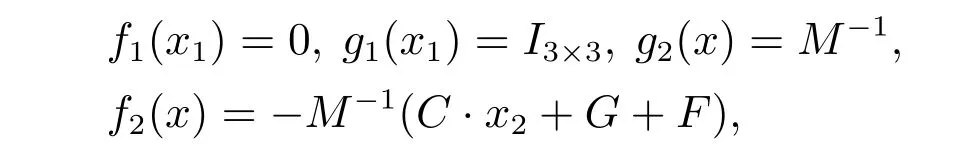
f1,f2,g1和g2在定义域D ⊂内是充分光滑的,并且g1(x)0,g2(x)0.

假设参考信号y∗,∗,∗已经通过求解逆运动学在线获得.

对系统(4)的输出端求导,可得

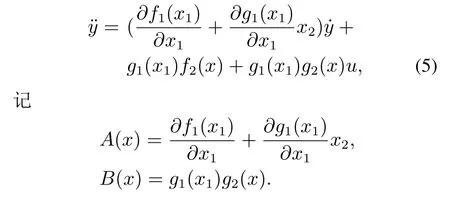
3.1 第1步:类稳态控制

该控制算法与当前测量或估计状态相关,而不依赖系统真实的稳态,所以称为类稳态控制.

3.2 第2步:变参考前馈控制

针对复杂系统,只通过稳态控制很难达到期望的性能.引入一个前馈控制uf,使控制律u=us+uf满足式(5).令则参考前馈控制律为

由式(7)可见uf与可变参考相关,反映了期望变化时系统相应的调节作用;同时uf的增益也与系统状态相关.

3.3 第3步:误差反馈控制

由推导的假设条件看出,系统在类稳态控制us与参考前馈控制uf作用下并不能保证输出达到参考值.为了使得实际轨迹渐近跟踪期望轨迹,在以上设计的基础上引入了误差反馈控制ue,得到控制律u=us+uf+ue.

定义系统跟踪误差为e1=y∗−y,将控制律代入式(5)中,可以将闭环系统误差写为

令e2=,则

为了使误差趋近于零,本文采用Backstepping方法推导控制律.将e2看作是虚拟控制,定义第1个李雅普诺夫函数为

选择虚拟控制输入

当e3→0时,e2趋近于,系统=−k1e1−e3渐近稳定.误差e3的动态特性满足

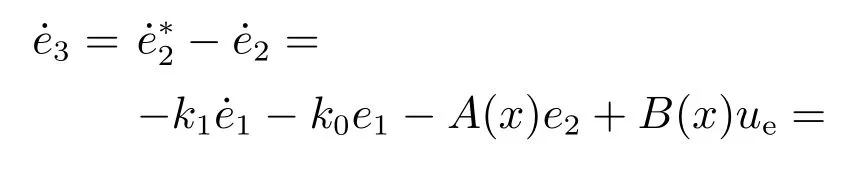
定义包含误差e3的李雅普诺夫函数

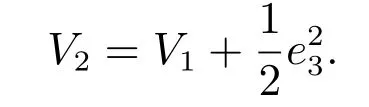
对上述李雅普诺夫函数求导,可得

当k3>0时,因此可保证实际轨迹对期望轨迹的渐近跟踪性能.

综上,系统整体的控制律

3.4 稳定性与鲁棒性分析

由于机械臂系统存在未建模动态、参数不确定性和外界扰动.为了分析问题方便,将系统存在的不确定性和扰动统一定义为加性扰动d∈R1,则有

将控制律(18)代入式(19)中,经过整理可以得到闭环误差系统动态

误差变量为χ,e1,e3,可见积分项的引入增加了误差系统的维数.取李雅普诺夫函数

求导可得

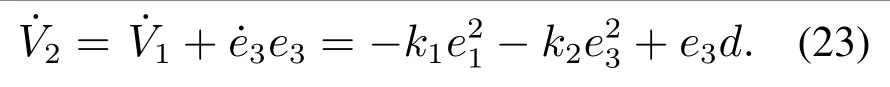
利用杨氏不等式,可以进一步得到

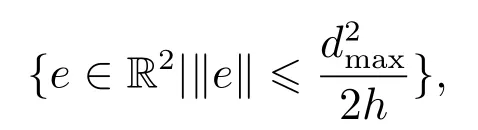
因此误差系统(20)−(22)对于扰动输入是输入−状态稳定的[26].

接下来对跟踪静差进行讨论,首先分别对误差系统进行拉氏变换.

在未引入积分项的情况下:

将E3代入E1(s)中,整理可得

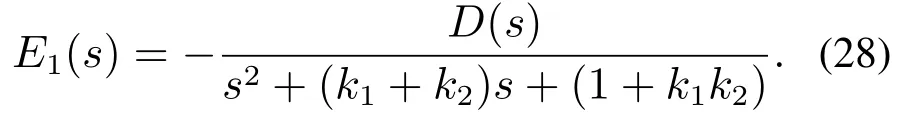
在引入积分项的情况下:

将E3I代入E1I(s)中,整理可得

对式(28)和式(31)使用终值定理,可以计算得到扰动D(s)引起的跟踪误差,

其中:kI=k1+k2,kw=1+k0+k1k2.

下面讨论不同类型扰动下稳态误差的大小.

1)当扰动d是脉冲信号时,其拉氏变换为D(s)=1,此时式(32)和式(33)中的稳态误差均为零,即e1(∞)=e1I(∞)=0;

2)当扰动d是阶跃信号时,拉氏变换此时未引入积分情况下的误差终值为

而引入积分后的误差终值仍为零,即e1I(∞)=0,这也说明积分有消除静差的作用;

3)进一步讨论积分修正后静差,如果扰动d是斜率为¯d的斜坡信号,则

一般来说,扰动的形式可能并不单一,通常很难确切知道,因此难以给出减小静差的k0,k2的选取原则.

根据对系统鲁棒性和稳态误差的分析,总结出如下的参数调整原则:

1)k1决定了跟踪误差e1的衰减快慢,k2决定e3的衰减快慢.从这个角度上看,k1和k2应该选择尽可能的大.但较大的k1和k2可能引起控制的高增益,造成噪声放大.

3)尽管很难给出k0的具体选取原则,但从式(35)来看,根据可接受的静差范围应该选择尽可能大的k0.

4 仿真结果

为了验证本文提出的控制器的有效性,采用MATLAB 2016b 针对3 自由度机械臂进行仿真实验,机械臂具体参数如表1所示.

表1 机械臂具体参数Fig.1 Parameters of mechanical arm

4.1 双纽线(lemniscate曲线)轨迹

设置参考轨迹为

图2为初值(x0,y0,z0)=(0.465,0.264,0.107)时基于三步法的末端无负载和负载10 kg的机械臂双纽线轨迹跟踪仿真结果.

图2 双纽线轨迹跟踪控制仿真结果Fig.2 Simulation results of lemniscate trajectory tracking control

图3为初值(x0,y0,z0)=(0.234,0.365,−0.134)时的末端负载10 kg的机械臂双纽线轨迹跟踪仿真结果.

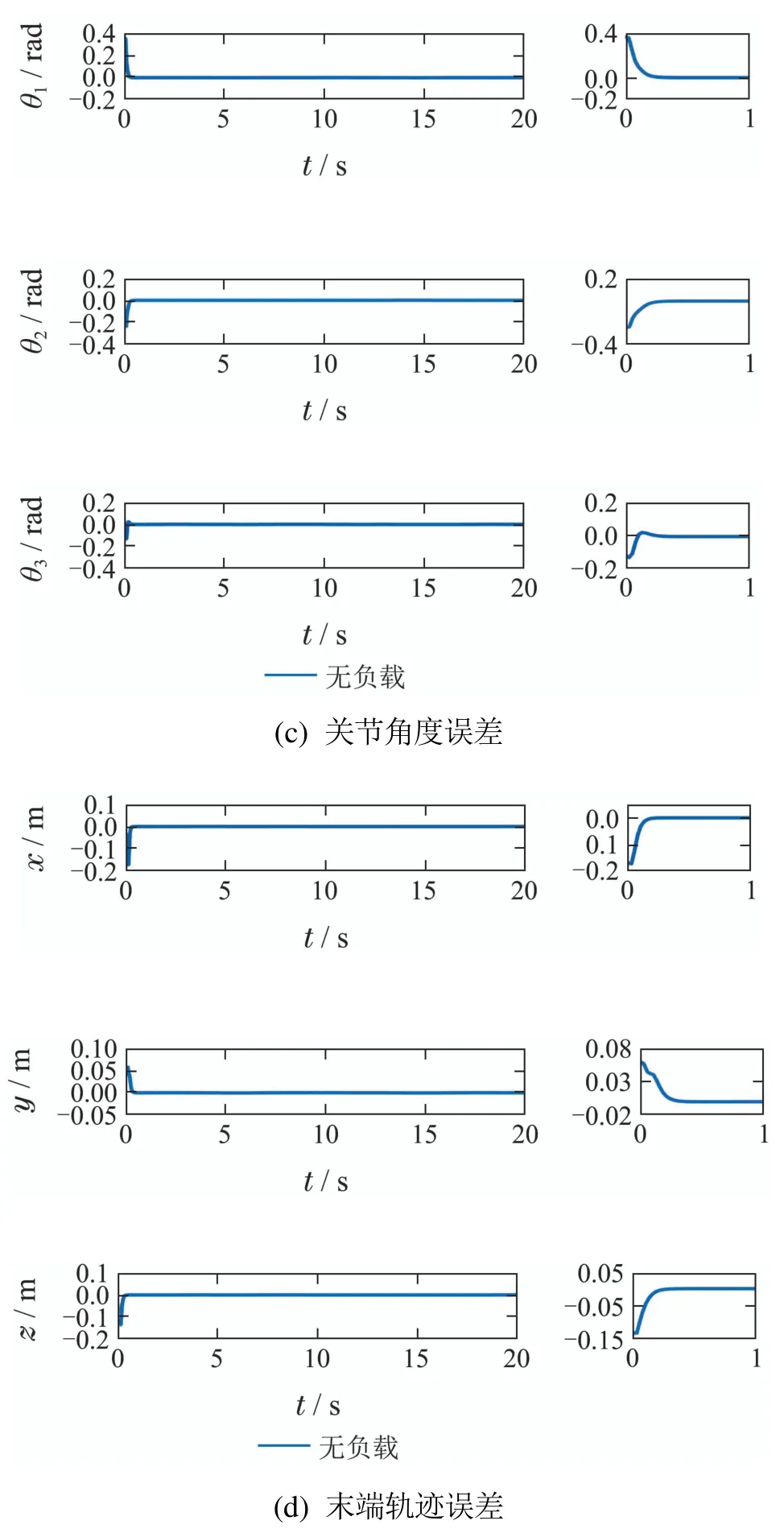
图3 变初值双纽线轨迹跟踪仿真结果Fig.3 Simulation results of lemniscate trajectory tracking with variable initial value

图4为初值(x0,y0,z0)=(0.597,0.408,0.109)时的末端负载10 kg的机械臂双纽线轨迹跟踪仿真结果.

图4 变初值双纽线轨迹跟踪仿真结果Fig.4 Simulation results of lemniscate trajectory tracking with variable initial value

4.2 空间圆柱螺线轨迹

设置参考轨迹为

三步法不仅可以实现双纽线轨迹跟踪,还可以完成对空间的圆柱螺线等轨迹的跟踪.

图5为初值

时基于三步法控制的末端无负载、负载10 kg的空间圆柱螺旋跟踪仿真结果.

图6−7分别为初值

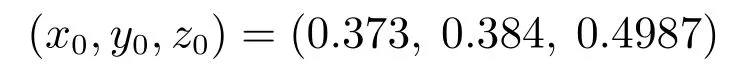
时无负载和负载10 kg时基于滑膜控制与三步法控制的空间圆形轨迹跟踪仿真对比结果.

图5 圆柱螺线轨迹跟踪仿真结果Fig.5 Simulation results of cylindrical spiral trajectory tracking

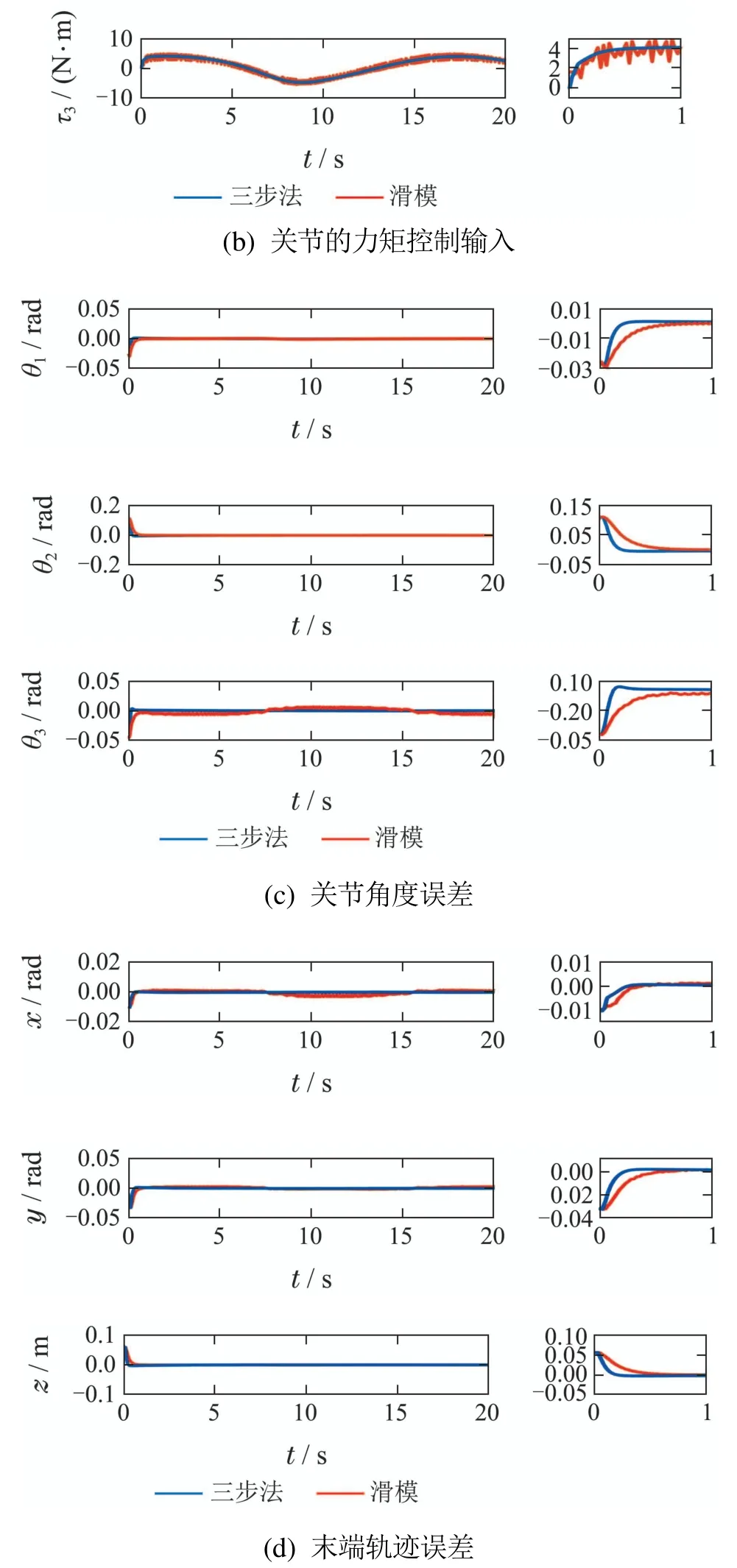
图6 无负载圆形轨迹跟踪仿真对比结果Fig.6 Comparison of simulation results of unloaded circular trajectory tracking

图7 负载10 kg圆形轨迹跟踪仿真对比结果Fig.7 Comparison results of circular trajectory tracking simulation for load 10 kg

4.3 空间圆形轨迹

设置考轨迹为

图8为初值

时的末端无负载且存在扰动d=3 sin(2t)的基于滑膜控制与三步法控制的空间圆轨迹跟踪仿真对比结果.

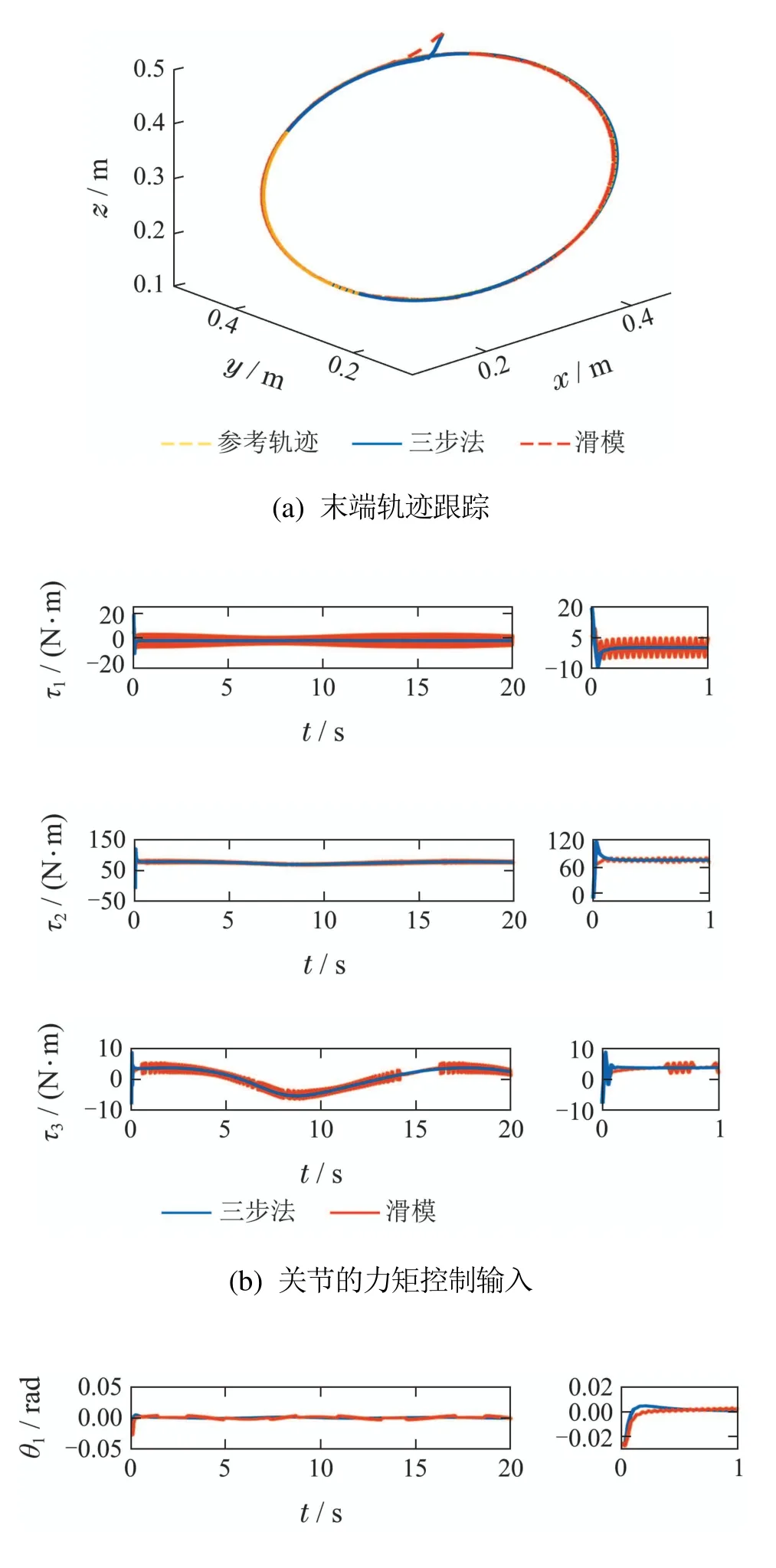
图8 扰动下的圆形轨迹轨迹跟踪仿真对比结果Fig.8 Simulation comparison results of circular trajectory tracking with disturbance

由图2可以看出当负载由零变为10 kg时,三步法控制器可以很好的控制机械臂跟踪双纽线轨迹,使得轨迹渐近收敛,各个关节的控制输入保持在合理的范围内,系统动态变化率不大,各关节角度与参考角度的稳态误差均在10−5rad以内,调整时间也均在1 s以内,两种负载情况在稳态误差与调整时间上没有明显的差距.由图3−4可以看出,三步法控制器的轨迹跟踪精度与初值无关.由图5可以看出,当负载由零变为10 kg时,三步法控制器依旧可以“稳、准、快”地使机械臂跟踪空间圆柱螺线,使得轨迹渐近收敛,并且在改变初值的情况下也可以快速且稳定地跟踪上参考轨迹,稳态误差在10−5rad以内,调整时间在1 s内.

图6−7可以看出,当负载由零变为10 kg时,在没有扰动存在的情况下,三步法控制器比滑模控制器的跟踪速度快,精度高并且不存在控制量抖振问题.图8可以看出,当存在一个正弦扰动时,三步法控制器相比于滑模控制器的抑制扰动能力更好,控制输出平稳,误差小且跟踪速度快.由上述仿真结果可以得出三步法控制器可以很好地控制机械臂渐近跟踪期望轨迹,并且对末端负载质量变化和扰动具有鲁棒性.

5 总结

本文设计了3自由度机械臂轨迹的三步法跟踪控制器,该控制器包括类稳态控制、参考前馈控制和误差反馈控制三部分.通过控制机械臂的关节角度使机械臂末端跟踪上期望轨迹.闭环系统是输入到状态稳定的,因而对扰动和未建模动态具有一定的抑制能力.仿真结果表明本文设计的控制器可以使机械臂快速地跟踪上期望轨迹、并且可以抑制末端负载质量变化等不确定性的影响.