电力线小波变换正交频分复用通信系统分析

刘 艳，张 峰，赵 黎，沈 波

(1.西安工业大学 电子信息工程学院，西安 710021；2.西安机电信息技术研究所，西安 710000)

wavelet transform;communication efficiency

电力线通信(Power Line Communication,PLC)是以现有的电力线网络作为通信介质来实现信息传输的技术。G3-PLC标准是一种电力线通信规范，是一个主要面向智能电网里的通信技术的全球开放性协议[1]。采用该标准的电力载波通信系统，由于利用基于快速傅里叶变换(Fast Fourier Transformation,FFT)为核心的正交频分复用技术，因此具有频谱利用率高，抗衰减能力强等特点，但其对正交性要求较高，一旦正交性遭到破坏就不能保证通信可靠性。文献[2]表明正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)因具有抗多径干扰和频率选择性等特点，非常适合在电力线载波通信系统中使用，但由于电力线信道特性恶劣，噪声显著且具有时变性;文献[3]表明传统的OFDM频谱利用率高，抗衰减能力强，但其对正交性要求较高，一旦正交性遭到破坏就不能保证通信可靠性；文献[4]研究表明基于小波变换的OFDM系统在电力线信道下的性能优于传统的OFDM系统,但目前还未用于G3-PLC系统。基于上述分析，文中基于离散小波变换(Discrete Wavelet Transformation,DWT)，提出性能更好的双正交DWT-OFDM调制解调算法应用于G3标准的电力载波通信中，优化通信系统性能，解决复杂信道环境下电力载波可靠通信的问题。

1 基于FFT-OFDM的G3-PLC系统性能

1.1 可靠性与效率分析

为对效率问题进行分析，循环前缀选取3种典型数值，设置为加入0个循环前缀，加入8个循环前缀和加入30个循环前缀，仿真分析如图1所示。

由图1分析可知，加入30个循环前缀，信号有效传输效率下降，仅能达到40%左右；若将循环前缀数减少到8，效率得到了一定提升，却降低了通信可靠性。加入30个循环前缀时，在信噪比为-11 dB时，误码率就可以达到10-4量级，但当加入的循环前缀数为8时，要在信噪比为-10 dB时，误码率才可以达到相同量级。

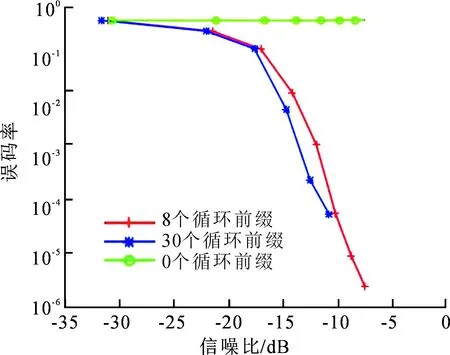
图1 FFT-OFDM不同循环前缀对比

1.2 峰均比特性分析

峰值平均功率比(Peak-to-Average Power Ratio,PAPR)为信号的峰值功率与平均功率的比值，简称峰均比。在OFDM系统中，高的PAPR值会降低射频放大器的功率和效率[5-6]。PAPR在给定阈值的情况下，随子载波数量N的加大，累积分布函数也会相应变小，相反数据符号超过PAPR阈值的概率就会相应的变大[7]。通过计算PAPR大于给定阈值z的概率，从而可得出互补累积分布函数(Complementary Cumulative Distribution Function,CCDF):

P{PAPR>z}=1-P{PAPR≤z}

=1-(1-e-z)N。

(1)

式中：z为阈值；N为子载波数量。

FFT-OFDM峰均比仿真分析如图2所示。

图2 FFT-OFDM峰均比

分析图2可知，在电力线信道环境下测得的峰均比特性很差，出现较高PAPR值的概率较高，达到10%左右，一旦超出线性范围，就必然会导致失真，从而对OFDM可靠性产生极大影响。

2 基于正交小波变换的G3-PLC系统

通过对基于FFT-OFDM系统的G3-PLC系统所存在的问题进行分析，建立性能更好的DWT-OFDM系统，并将其应用于G3标准的电力载波通信。

2.1 正交小波变换

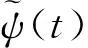
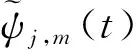
2.2 小波分解与重构算法

设φj,k与φj,k分别为尺度函数与小波函数，为了将空间Vj中的信息分解到子空间Vj-1和Wj-1中去，分别由{f,φj-1,k}决定空间Vj-1，{f,φj-1,k}决定空间Wj-1，信号f∈空间(Vj)，j为分辨率，因此对信号进行分解，即

(2)

利用式(2)以及基函数{φj,k}的正交性，在式(2)中分别取f=φj,k，而信号分解与重构过程又可以按照系数的形式给出，过程如下：

(3)

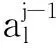
(4)

2.3 基于正交小波变换的G3-PLC模型

将正交小波变换OFDM系统应用于G3标准的电力载波通信系统中，信号传输模块可按图3所示的结构进行设计。信号发送前要进行循环冗余校验(Cyclic Redundancy Check， CRC)(CRC 校验采用CRC-16标准)，二进制相移键控(Binary Phase Shift Keying,BPSK)映射，四相相移键控(Quaternary Phase Shift Keying,QPSK) 映射，逆离散小波变换(Inverse Discrete Wavelet Transform,IDWT)和模拟前端(Analog Front End,AFE)放大等过程。信号接收端需进行自动增益控制(Automatic Gain Control,AGC)和分离帧控制头(Frame Control Head,FCH)等过程。文中采用Reed-Solomon编码(以下简称为RS编码)和Reed-Solomon解码(以下简称为RS解码)。

G3-PLC标准的物理层可分为2个模块，上半部分为发送模块，下半部分为接收模块。

发送端工作过程：基带信号先需要经过循环冗余校验，目的是判断接收到的数据和发送数据是否相同；RS编码是一种前向纠错编码，对输入的信号进行编码处理，再对编码后的数据进行交织，改变数据流的传输顺序，将突发错误随机化，提高系统纠错的能力[8]；G3-PLC标准支持BPSK和QPSK两种调制方式[9]，信号通过IDWT变换，可以消除载波间干扰和符号间干扰，此外，还需要对信号进行加窗处理以防止频谱泄露[10]；将FCH位、数据位与前导进行级联，数据经过模拟前端放大滤波器及耦合变压器，传输至电力线上。接收端工作过程：接收模块的流程为发送模块的逆操作，电力线上传输的信号经滤波及AGC处理，然后进行解调得到原始的信号。

图3基于小波变换的G3-PLC物理层结构

Fig.3Physical layer structure of G3-PLC based on DWT

3 实验仿真分析及性能优化

3.1 仿真参数设定

根据电力载波通信中G3标准的要求，在Matlab2015b软件中进行仿真实验，信道为实际的电力线信道，调制方式为BPSK。为保证实验的可信度，每个信噪比(Signal Noise Ratio,SNR)进行1 000次仿真，且每个信噪比对应的误码率为1 000次仿真的均值。仿真参数见表1。

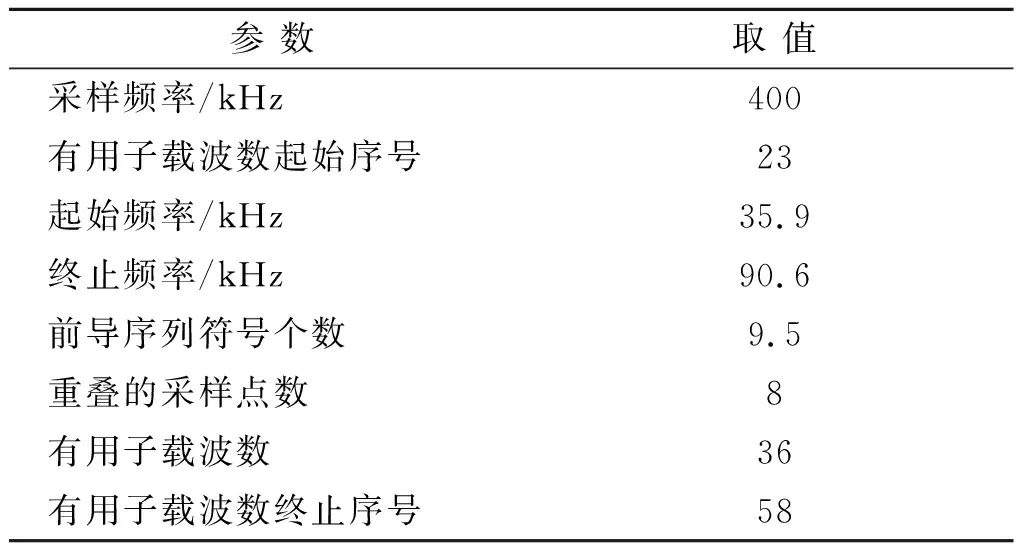
表1 G3-PLC物理层参数

3.2 可靠性分析

3.2.1 不同小波基对可靠性的影响

根据小波基的不同种类[11-12]，分满足正交性且满足对称性的小波基，满足正交性不满足对称性的小波基，满足正交性和近似对称性的小波基，满足对称性但不满足正交性的小波基4种类型的小波基进行分析，每种选取一个典型小波基进行仿真实验，实验结果如图4所示。

图4 不同小波基对比图

由图4可知，小波基bior6.8效果最优，这是因为该小波满足双正交性，在双正交多分辨率分析的框架下，尺度函数与小波函数关于时间平移参数都不是正交的，双正交要求当尺度函数与小波函数作时间与频率伸缩后得到的函数与其对应的对偶函数满足正交条件，正交小波变换中小波函数与其对偶函数可以具有不同的紧支集长度以及不同的消失矩，可获得更高效的信号重构。

3.2.2 实测电力线信道下的可靠性分析

在实测电力线信道环境下，分别对DWT-OFDM系统及FFT-OFDM系统进行仿真分析实验，结果如图5所示。

图5 DWT-OFDM系统与FFT-OFDM系统对比图

由图5可知，基于小波变换的OFDM系统性能更好，在误码率为10-2时，基于小波变换的OFDM系统比基于快速傅里叶变换的OFDM系统信噪比有9 dB左右的提升；在-20 dB时，DWT-OFDM系统误码率可以达到10-3量级，而FFT-OFDM系统仅能达到10-1量级。

3.3 通信效率分析

为全面分析系统性能，在相同仿真环境下，对DWT-OFDM系统进行仿真分析，针对不同循环前缀个数，设置4种典型值，结果如图6所示。

图6 不同循环前缀数对比图

由图6可知，采用8个循环前缀的误码率性能更好，这是由于在每个OFDM符号前添加循环前缀的情况下，系统会线性增加相同比例的噪声，致使添加30个循环前缀的误码率性能不如添加8个循环前缀的误码率性能。通信效率数值分析见表2。

表2 通信效率对比

3.4 峰均比特性分析

为更好衡量系统的性能，对FFT-OFDM系统及DWT-OFDM系统进行了峰均比特性的分析验证，结果如图7所示。

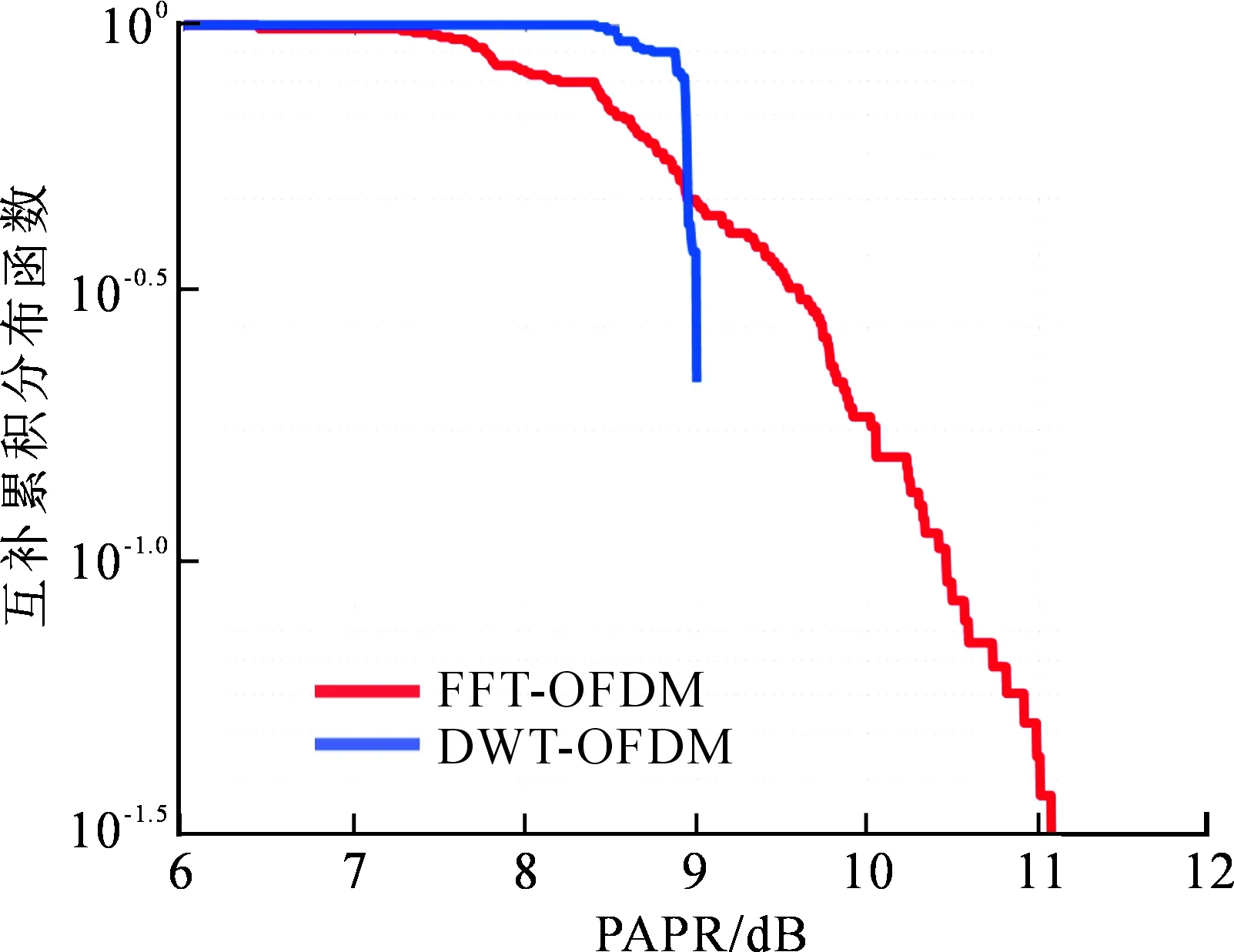
图7 DWT-OFDM系统和FFT-OFDM系统峰均比特性

由图7可知，相比基于快速傅里叶变换的OFDM系统，基于小波变换的OFDM系统峰均比性能更好，出现较高峰均比的概率较低。这是由于基于FFT的OFDM系统将若干个子载波信号在时域上进行叠加，若子载波符号存在相同相位，则会造成高的时域功率峰均比，而DWT-OFDM系统的子载波仅在不同空间上才会形成较高的PAPR，同一子空间中的满足平移正交性的子载波存在一个天然的相位差，不可能完全同相，故不会形成较高的峰均比。

4 结 论

文中在研究不同小波基通信可靠性的基础上，将正交DWT-OFDM调制解调算法应用于G3标准的电力载波通信中，对通信效率、峰均比进行了分析；并在3种不同信道下对通信可靠性进行分析测试。通过理论与实验分析，得到结论为

1) 正交小波尺度函数和小波函数均满足正交小波基条件，具有较好的正则性，可保证小波系数重构的稳定性；在正交小波变换中小波函数与其对偶函数可以具有不同的紧支集长度以及不同的消失矩，可获得更高效的信号重构。

2) 在数据传输速率方面，基于小波变换的OFDM系统采用小波作为子载波，可减少添加循环前缀的个数，添加8个循环前缀个数时效率可达到最优，传输效率高于经典OFDM系统。

3) 在峰均比特性方面，相较于FFT-OFDM系统，正交DWT-OFDM系统峰均比性能更好，可减小信号峰值超出非线性器件的线性范围概率，保证信号有效传输。