非对称构型多站时差定位系统定位精度分析

张 欢，周云生，段志慧

非对称构型多站时差定位系统定位精度分析

张 欢，周云生，段志慧

（北京遥测技术研究所 北京 100094）

以空间四站时差定位系统为例对多站时差定位系统原理进行阐述，推导定位系统的定位精度并分析影响系统定位精度的因素。通过仿真分析多站时差定位系统在不同空间构型、站间距、时差测量误差、位置误差条件下对地面辐射源的定位精度得出：多站时差定位系统的空间构型直接影响定位精度，主辅站间距长度越长定位精度越好；各站位置误差比时差测量误差对定位精度的影响更大；对于多站定位系统出现的非对称空间构型，通过合理的布站优化可以提升对某一固定辐射源的定位精度。

多站时差定位；辐射源定位；定位精度分析；非对称构型

引 言

辐射源情报信息是现代信息对抗技术最重要的基础。利用安装在小型化侦察设备上的侦察任务载荷获得战场雷达辐射源的情报信息，从而实现对该辐射源的侦察定位，完成辐射源信息的实时感知，并为后续的定向电子干扰或反辐射武器引导提供支持[1,2]。多站时差定位系统因其具有定位精度高、定位速度快（单次时差测量即可实现辐射源定位）的特点，并且能够适应辐射源多种类型信号，因此在电子侦察定位中得到广泛应用。多站时差定位系统通过系统中各站分别测量同一部雷达辐射源的脉冲信号，通过脉冲配对与参数测量获得同一个脉冲信号的到达时间（TOA），两两相消得到独立的到达时间差（TDOA），利用四个侦察设备可以得到三组独立的时差值，每一组独立的时差可以确定一个定位双曲面，辐射源位置即位于三个双曲面的交点处[3]，无需额外的先验信息即可完成辐射源定位。近年来，关于多站时差定位系统在理想构型下的定位问题研究很多[4-8]，这些文献主要分析了多种理想空间构型下定位精度，如Y型构型、T型构型等等。在实际情况中，辐射源定位系统由于使用条件的限制，各站均处于运动状态，导致各站之间的间距不一致且随时变化，各站之间的空间构型为非对称构型，进而影响对辐射源的定位精度。

因此，本文对四站时差定位系统进行研究，研究了时差定位系统原理与定位精度分析，分析了对时差定位精度造成影响的因素。在此基础上，以Y型构型为例，重点研究了时差定位系统在非典型对称构型下对地面辐射源的定位精度，对各站间距长度、各站连线夹角、主辅站高度差以及系统误差对定位精度的影响进行了仿真分析。

1 四站时差定位系统模型

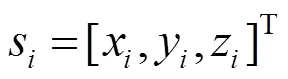
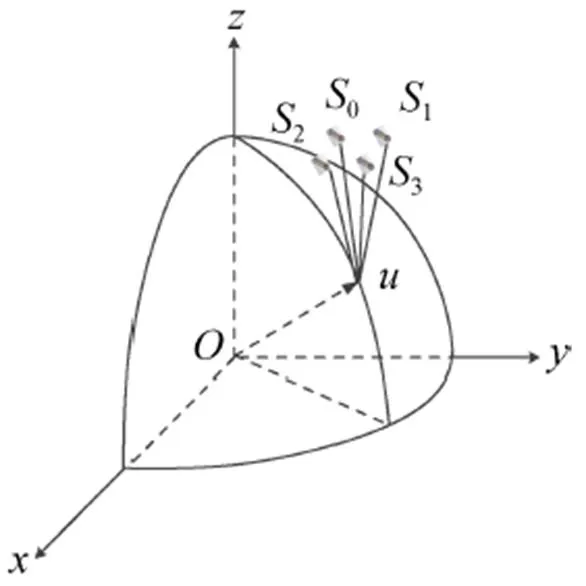
图1 时差定位系统模型

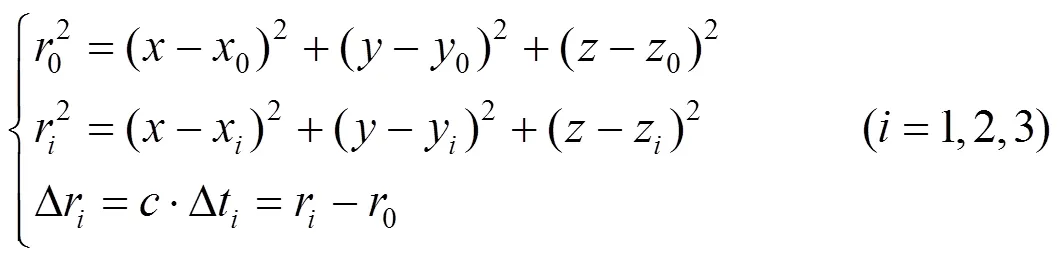
求解定位方程组（1），可对辐射源进行定位。对于定位方程组（1）的求解，已有许多文献[8,9]探讨，本文不再赘述。由于定位系统中存在时差测量误差，且各站均处于运动状态，其自身位置信息存在误差，在求解方程组的过程中会出现模糊或无解情况。为了消除定位模糊解或无解的情况，需要增加其他辅助测量信息或根据辐射源的先验信息进行处理。

2 定位精度分析

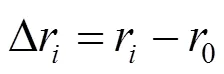
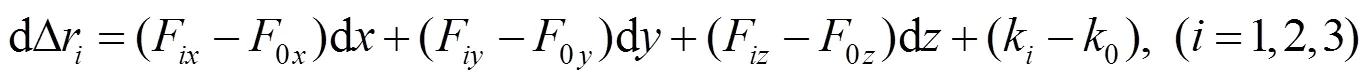
式中

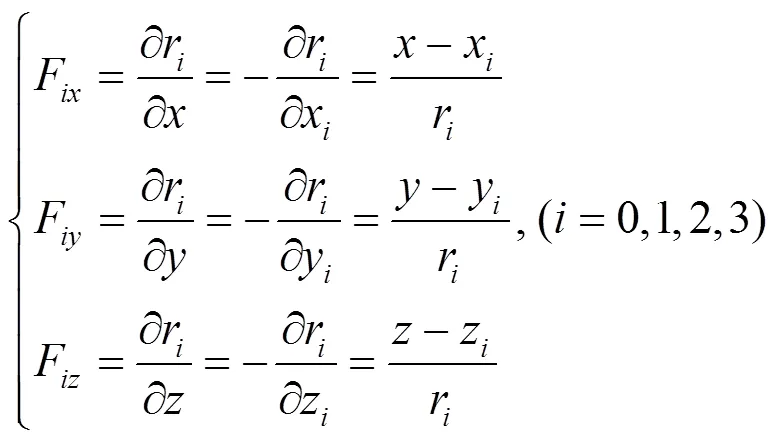
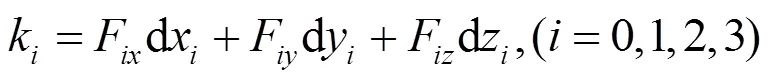
将式（2）写成矢量形式为

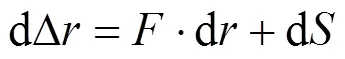
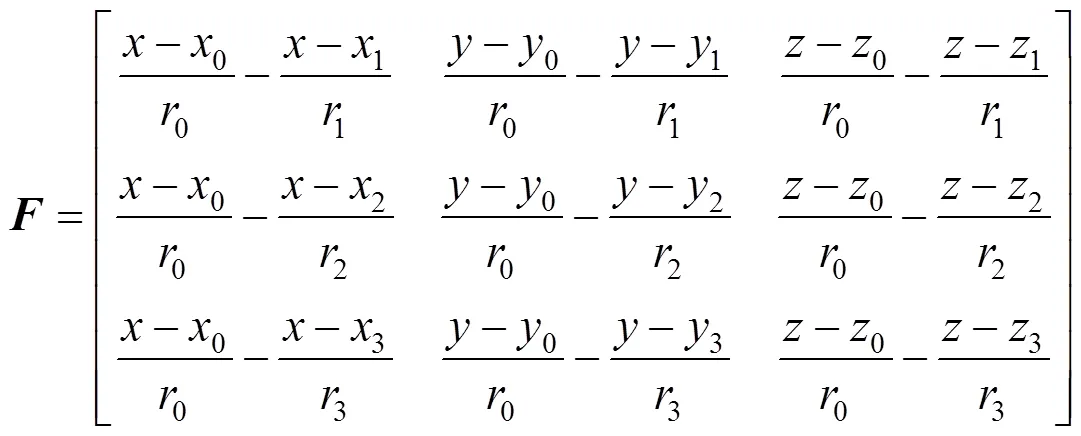
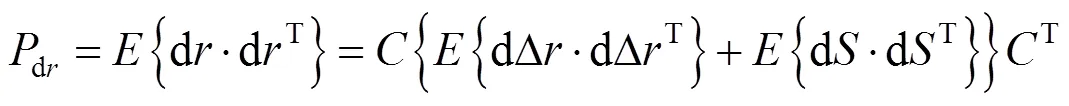
其中，

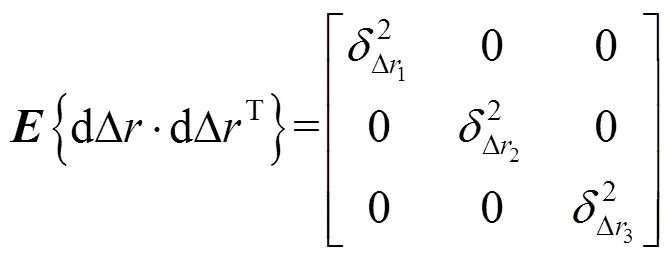
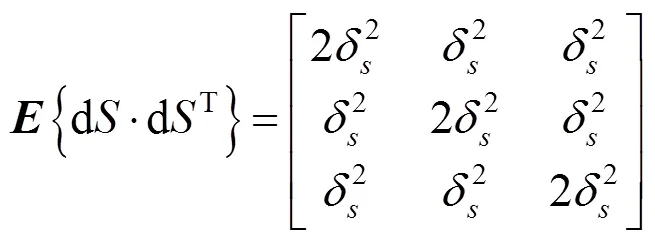
由此可知，四站时差定位系统的为

GDOP可作为定位精度的衡量尺度，通常情况下，定位系统与辐射源之间的距离越远，定位精度越差。因此定义相对定位误差为

其中为定位系统与辐射源的距离，相对定位误差可以反应定位精度与距离之间的关系。因此，本文中选择相对定位误差作为验证定位精度的标准。

3 仿真分析

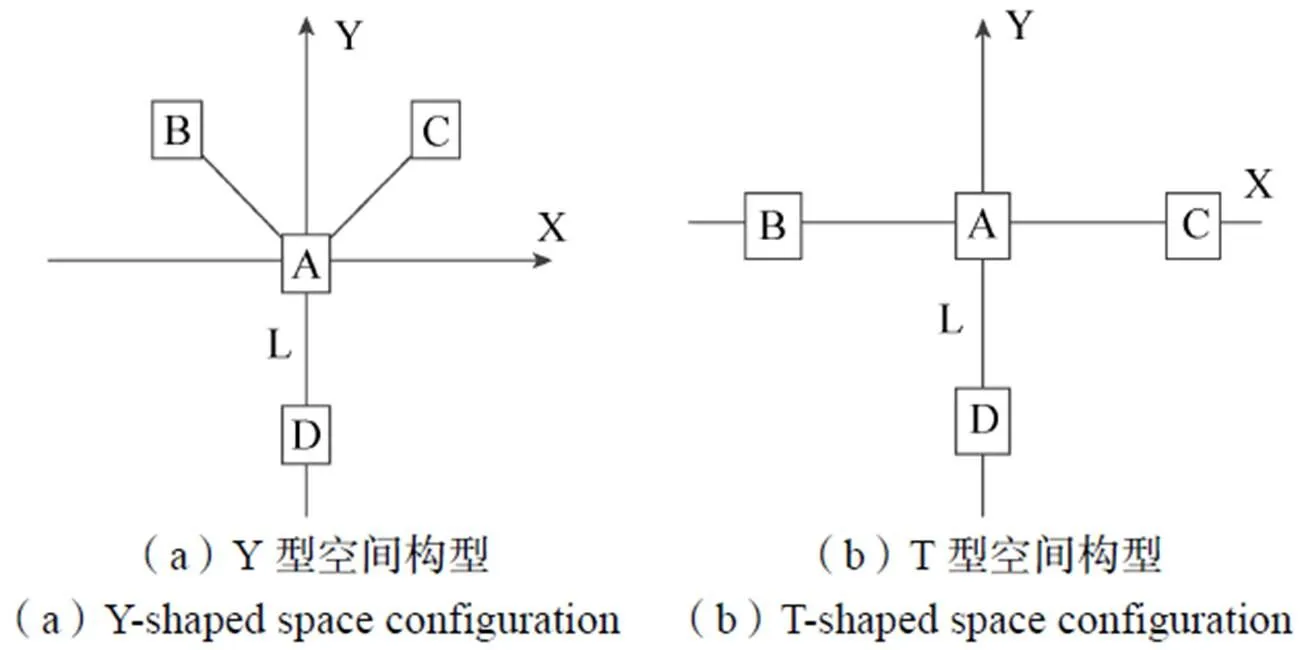
图2 空间对称拓扑结构

在实际情况中，由于平台要求的限制，各站之间的间距不一致且随时变化，导致各站空间构型不规则。由定位精度分析可知，影响时差定位系统定位精度的因素有：系统中各站空间构型、主辅站之间站间距、时差测量误差以及位置误差等等。本文分别对上述影响定位精度的因素进行仿真分析。

3.1 仿真1：空间构型对定位精度影响分析

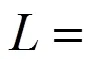
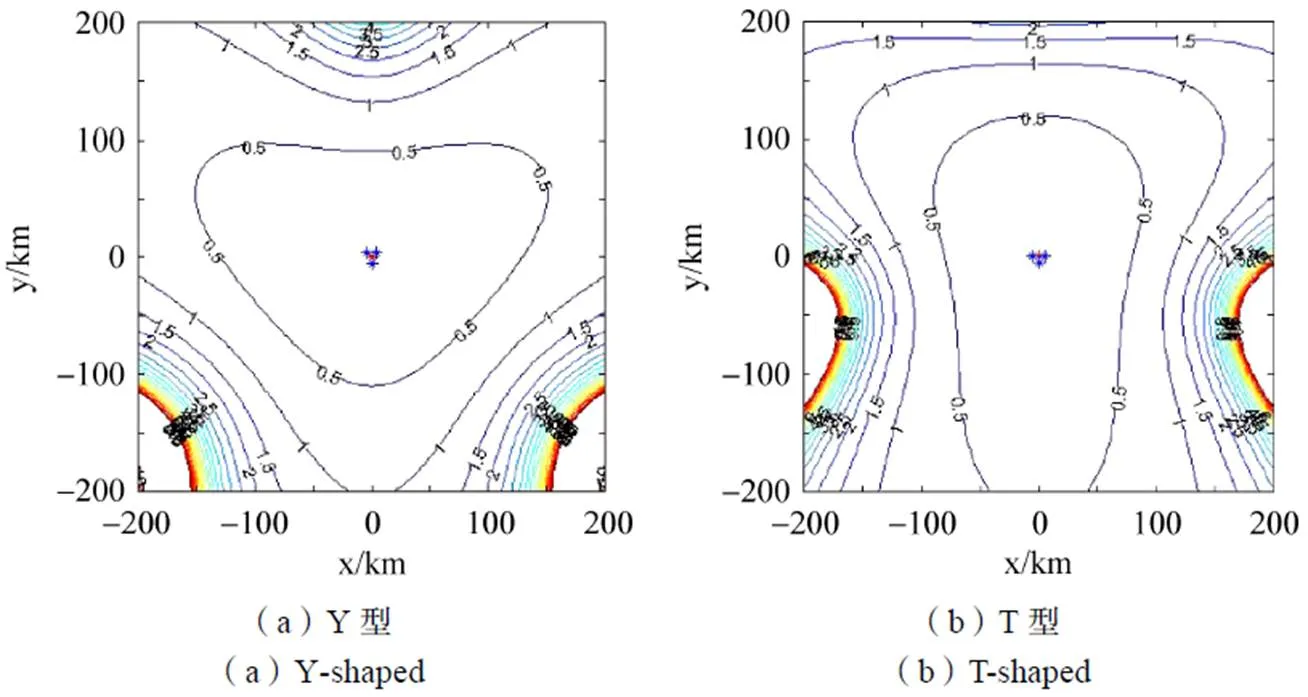
图3 不同空间构型下定位精度分布情况

由图3可以看出，时差定位系统中各站空间构型直接影响了时差定位的定位精度。在Y构型的100km范围内，定位精度都可以达到1%R，辐射源位于任何方向上的定位误差变化基本相同，在主站与辅站连线延伸方向上的定位精度较好，更适合用于对全方位进行搜索定位；T构型的定位精度接近于Y构型，当辐射源位于T指向方向上时定位精度更好，在距离200km上可以达到0.5%R，但在三站连线方向上的定位精度下降。因此，下文在对其他因素进行仿真分析时，定位系统采用Y构型。

3.2 仿真2：对称构型下间距长度对定位精度的影响分析

本节仿真定位系统在对称构型下间距长度对定位精度的影响。定位系统采用Y构型，间距长度分别取3km、6km，空间构型采用Y型，其余仿真条件与仿真1相同，仿真结果如图4所示。

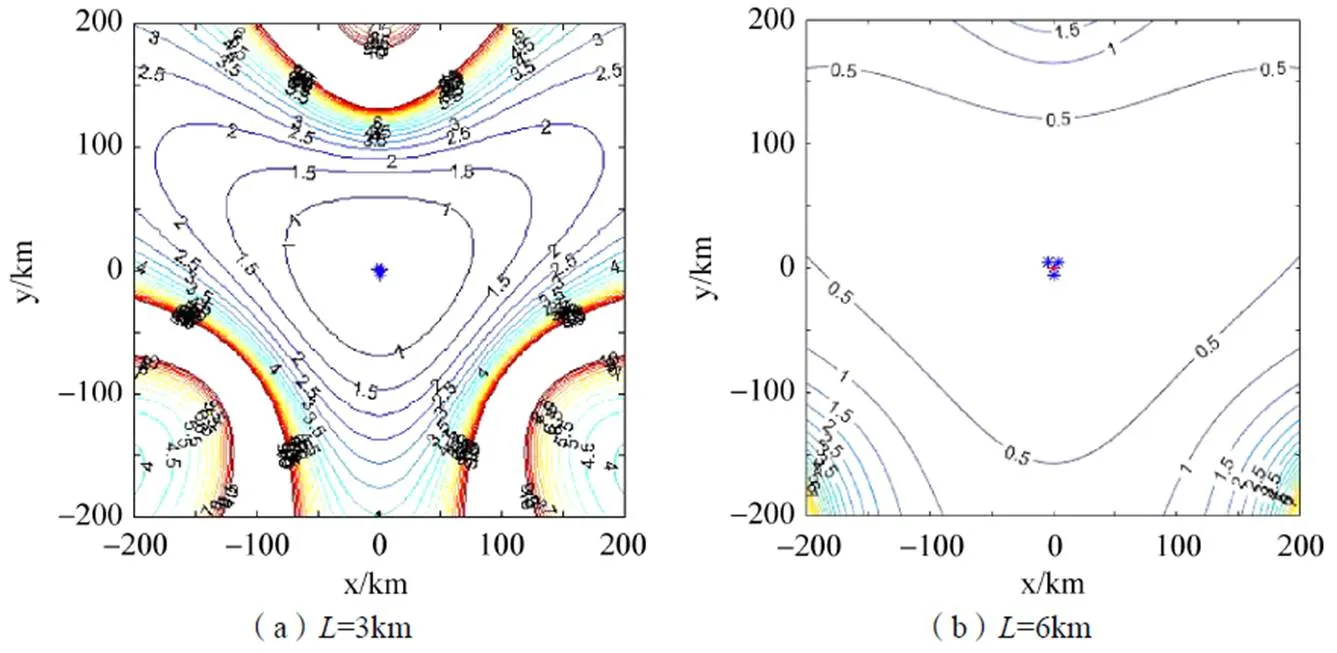
图4 不同间距长度下定位精度分布情况

由图4可以看出：当间距长度为6km时，在200km范围内定位精度可以达到1%R；当间距长度为3km时，只能在50km范围内达到1%R定位精度，定位精度急剧下降。站间距增加一倍，定位精度可以提高到原来的4倍，这是由于间距越短，定位精度受系统误差的影响越大，定位精度降低。因此，如果定位系统中各站间距较短，需要提高时差测量与自定位精度。

3.3 仿真3：对称构型下系统误差对定位精度的影响分析

时差定位系统中存在时差测量误差以及各站位置误差等等。考虑各站接收机同步、信号噪声等因素的影响，实际时差测量误差大约可以达到10ns~50ns。因此，在仿真1的条件下，将时差测量误差减小为10ns，位置误差取20m，其余仿真条件相同。仿真结果如图5（a）所示。考虑实际使用中，各站处于独立时变的运动状态，给各站的自定位带来误差，位置误差也会使定位精度恶化。因此，在上文的条件下，时差测量误差取30ns，各站位置误差减小为10m，其余仿真条件相同，仿真结果如图5（b）所示。

图5 不同误差下定位精度分布情况

仿真结果表明，与图3（a）相比，时差测量误差减小为10ns对定位精度分布影响较小，定位精度0.5%R的分布范围几乎没有变化；位置误差减小为10m，定位精度0.5%R的范围扩大了一倍。所以，相比于时差测量误差，位置误差对定位精度的影响更大。

3.4 仿真4：非对称构型对定位精度的影响分析

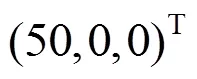
图6为辅站C的间距长度改变时定位精度的变化情况。仿真结果表明：定位系统主辅站间距长度的增加，对某一固定辐射源的定位精度提高，符合定位精度分析的基本策略。

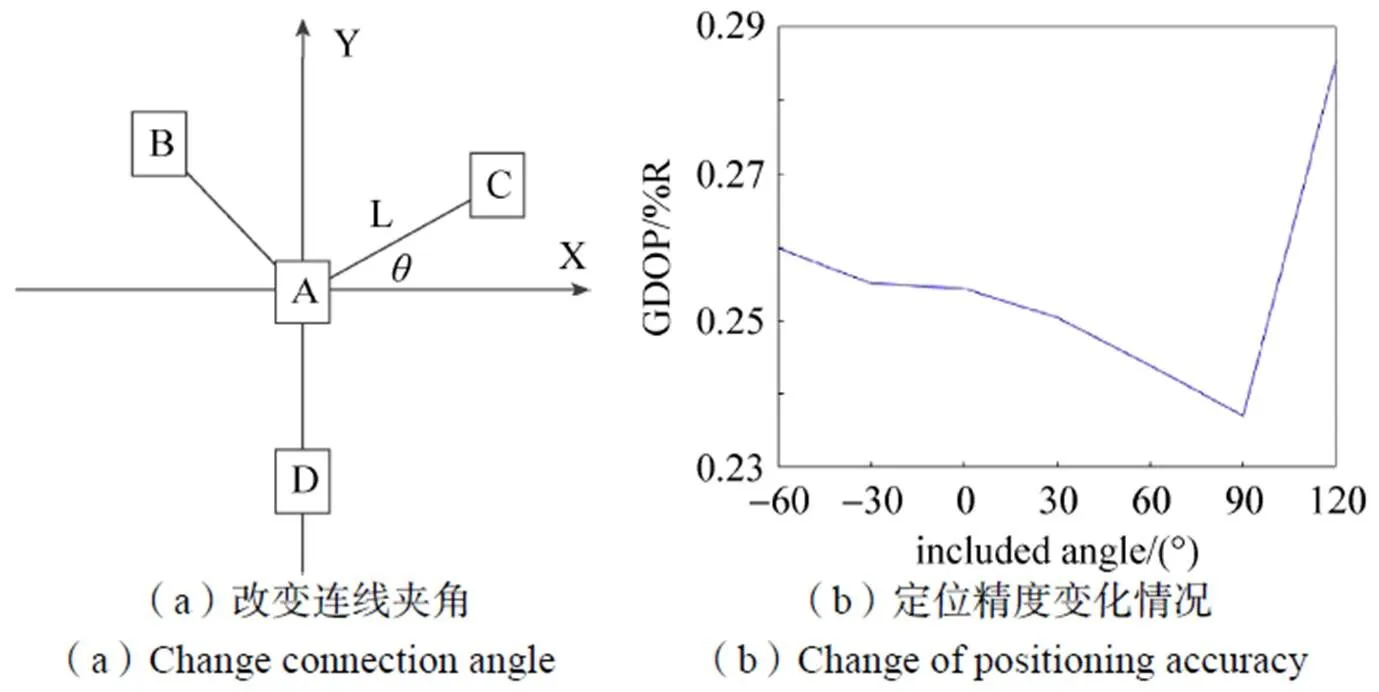
图7 主辅站连线夹角改变对定位精度的影响

图8为辅站C与主站A高度差改变时定位精度的变化情况，由于改变了辅站C与主站A的高度差，辅站B，C，D不再位于同一高度上。仿真结果表明：增加某一辅站的高度，对该站方向上的辐射源定位精度增加。

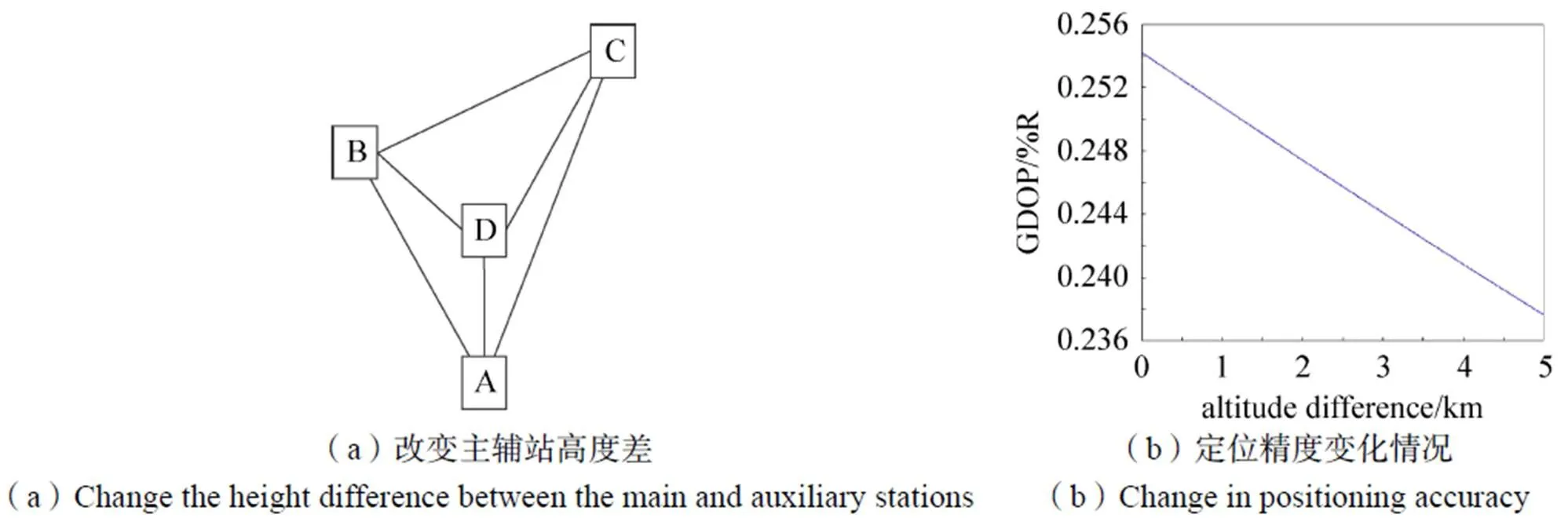
图8 主辅站高度差改变对定位精度的影响

上述仿真结果表明，对于实际使用中定位系统空间构型非对称的情况，可以通过增加主辅站的间距长度、合理改变连线夹角以及增加辅站高度的手段，提升某一特定辐射源的定位精度。

4 结束语

本文以四站时差定位系统为例，阐述了多站时差定位原理并推导了四站时差定位系统的定位精度，分析了定位系统在典型对称构型下各种因素对于定位精度的影响。在此基础上通过改变定位系统中某一辅站的间距长度、连线夹角以及主辅站高度差因素形成非对称的空间构型，选择某一固定辐射源，分析了条件改变时对该辐射源定位精度的变化情况。通过仿真得出如下结论：①无源时差定位系统的空间构型直接影响了对辐射源的定位精度，主辅站间距长度越长定位精度越好；②与时差测量误差相比，由于定位系统中各站运动产生的位置误差对定位精度的影响更大；③无源定位系统在实际使用中通常会出现非对称的空间构型，通过合理的布站优化可以有效提升对某一固定辐射源的定位精度。

本文分析了非对称构型下时差定位系统的定位精度变化规律，并针对特定的辐射源提出了相应的提高定位精度的方法，对实际应用具有一定理论指导作用。本文下一步将继续进行高精度时差测量算法以及定位算法的研究。

[1] 郭福成, 樊昀, 周一宇, 等. 空间电子侦察定位原理[M]. 北京: 国防工业出版社, 2012.

[2] 贾兴江. 运动多站无源定位关键技术研究[D]. 北京: 国防科学技术大学, 2011.

[3] CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905–1915.

[4] 俞志强. 四站时差定位精度分析[J]. 空军雷达学院学报, 2010, 24(6): 400–402. YU Zhiqiang. Analysis of 4-station TDOA location accuracy[J]. Journal of Air Force Radar Academy, 2010, 24(06): 400–402.

[5] 张政超, 童力. 四站时差无源定位精度分析[J]. 中国电子科学研究院学报, 2010, 5(6): 582–585. ZHANG Zhengchao, TONG Li. Precision analysis of passive location of 4-stations based on TDOA[J]. Journal of China Academy of Electronics and Information Technology, 2010, 5(6): 582–585.

[6] 任源博. 四星时差定位精度分析[J]. 电子科技, 2015, 28(6): 24–27. REN Yuanbo. Precision analysis of 4-satellite location based on TDOA[J]. Electronic Science and Technology, 2015, 28(6): 24–27.

[7] 张义超, 乔夏君, 陆浩然, 张镇琦. 低轨四星时差定位技术研究[J]. 计算机测量与控制, 2017, 25(5): 165–168. ZHANG Yichao, QIAO Xiajun, LU Haoran, ZHANG Zhenqi. Research of location technology on TODA with four LEO satellites[J]. Computer Measurement & Control, 2017, 25(5): 165–168.

[8] 顾黎明, 赵砚, 朱建丰, 缪善林. 四星时差定位中的卫星构型及其定位性能[J]. 电讯技术, 2017, 57(1): 33–38. GU Liming, ZHAO Yan, ZHU Jianfeng, MIAO Shanlin. Constellation configuration and its performance based on TDOA with four satellites[J]. Telecommunication Engineering, 2017, 57(1): 33–38.

[9] 郑仕力, 董乔忠. 基于高低轨联合的空中目标三维定位侦察技术[J]. 航天电子对抗, 2018, 34(2): 25–28, 60. ZHENG Shili, DONG Qiaozhong. Three-dimensional localization of aerial target based on joint high-and-low orbit satellites[J]. Aerospace Electronic Warfare, 2018, 34(2): 25–28, 60.

[10] 吴福平, 邓皓, 何建华. 影响多站时差定位精度的关键因素分析[J]. 航空科学技术, 2018, 29(5): 32–37. WU Fuping, DENG Hao, HE Jianhua. Key factors analysis of multi-stations TDOA passive location precision[J]. Aeronautical Science and Technology, 2018, 29(5): 32–37.

Location precision analysis of multi-station TDOA location system with non-symmetric configuration

ZHANGHuan, ZHOU Yunsheng, DUAN Zhihui

（Beijing Research Institute of Telemetry, Beijing 100094, China）

This paper takes the space four-station time difference positioning system as an example to explain the principle of the multi-station time difference positioning system, derives the positioning accuracy of the positioning system and analyzes the factors that affect the system positioning accuracy. Through simulation multi-station location system different spatial configurations, station spacing, the time difference measurement error, the position error of the positioning accuracy in the condition of the ground radiation derived: multi-station spatial configuration location system directly affect the positioning accuracy, the longer the distance between the main and auxiliary stations, the better the positioning accuracy; the position error of each station has a greater influence on the positioning accuracy than the time difference measurement error; for an asymmetric spatial configuration of the multi-station positioning system, by rational station optimization can improve the positioning accuracy of a fixed radiation source.

Multi-station TDOA location; Radiation source localization; Location precision analysis; Non-symmetric configuration

TN971

A

CN11-1780(2020)01-0019-07

Email:ycyk704@163.com

TEL:010-68382327 010-68382557

2019-12-30

张 欢 1995年生，在读硕士研究生，主要研究方向为无源定位。

周云生 1963年生，博士，研究员，主要研究方向为信息对抗。

段志慧 1977年生，硕士，研究员，主要研究方向为信息对抗。