基于变差的遥测天线跟踪稳定度研究*

陈建友，庞岳峰，刘津津，谢克佳

基于变差的遥测天线跟踪稳定度研究*

陈建友，庞岳峰，刘津津，谢克佳

（酒泉卫星发射中心 酒泉 732750）

对遥测系统伺服跟踪数据进行处理，分析对比几种跟踪方式，指出几种跟踪方式中可能存在的问题，并提出相应的改进措施。同时，通过曲线变差、方差的属性分析，研究自主跟踪时天线俯仰、方位的稳定度与跳变程度，并与理论弹道、数字引导方式的曲线稳定度进行分析和对比，得出变差越大稳定度越差，方差越大异常跳变越明显的结论。

遥测天线；自主跟踪；稳定度；变差

引 言

飞行器测量控制系统的主要设备包括光学设备和无线电设备两大类，其中利用接收或者发射的无线电信号对目标进行跟踪、测量、控制等多种功能的无线电设备，统称为无线电跟踪测量系统，其中最常见和常用的设备是遥测设备[1-4]。遥测设备将一定距离外被测对象的参数，经过感应、采集、信号变换，再通过传输介质传送到接收地点进行解调、记录、处理和显示，完成上述功能的设备组合称为遥测系统，是导弹、航天飞行器等系统不可缺少的重要组成部分[5,6]。在导弹与航天器研制阶段，遥测系统获取导弹与航天飞行器各系统的工作状态参数和环境数据，为检验导弹与航天飞行器的性能、进行故障分析提供依据。导弹与航天飞行试验耗资巨大，每次试验必须尽可能多地获取各种数据，所以遥测系统的性能优劣直接影响到导弹与航天飞行器的研制进程及费用，影响着武器性能的改进与提高。在导弹作战与使用阶段，遥测设备已成为武器的一个组成部分，它所获取的数据为判断导弹是否命中目标提供信息[7,8]。

遥测系统一般能够同时接收、解调几路遥测信号[9,10]。伺服分系统是具有速度环和位置环的双环路控制系统，它根据遥测接收信道产生的跟踪误差信号，或者由其他引导设备给定的指定信号与天线指向信号相比较产生的误差信号，经过变换、数字处理、放大，驱动天线指向预定目标[11]。

遥测天线具有扫描搜索、自动跟踪、手动跟踪、程序跟踪、记忆跟踪、数字引导跟踪等多种跟踪方式，根据需要选择合适的跟踪方式[12,13]。使用MATLAB实验对遥测伺服记录数据进行分析，直观显示跟踪角度曲线，可以判断是否是异常的情况，并通过对比研究，可以分析评价各种跟踪方式的性能。遥测天线的指向与飞行器目标之间的角误差需要在天线的波束范围之内，否则会减弱遥测信号的接收性能，影响数据质量。遥测天线能够稳定自主跟踪，是保证稳定接收、解调遥测信号的前提条件。但是，遥测天线自主跟踪有时候会表现出很不稳定的特征，影响跟踪效果、数据质量、设备寿命，这时候需要一种能够衡量判断天线跟踪稳定度的方法[14]。为了衡量跟踪方式的稳定度，本文提出基于变差属性的自动衡量方法，并通过MATLAB实验进行了对比验证。

1 基于MATLAB的遥测天线跟踪方式分析

弹道是指飞行器的飞行轨迹，有大地坐标系、发射系、空间大地直角坐标系等多种表示方式，在伺服分系统上表现为俯仰与方位角度，这是根据飞行器位置与遥测天线的大地坐标进行换算得到的[15]。遥测设备自主跟踪的方位、俯仰角度为遥测天线的实时角度，对应飞行器的实时跟踪位置；数字引导的方位、俯仰角度对应的是数字引导实时差分解算的飞行器实时位置；程序引导的方位、俯仰角度对应的是按照理论弹道飞行的目标位置。

伺服天线跟踪方式具有不同的功能，在不同的时机使用，且每次任务需根据飞行弹道特点制定完善最合适的跟踪方案。一般在任务开始前，手动控制天线，对准遥测发射机安装位置，在接收到遥测信号后通过手动方式调整天线至最佳位置。在目标起飞初始段，由于飞行偏离理论弹道，一般使用程序引导，即天线按照理论弹道运转。当目标飞行至一定高度，天线切换为自跟踪方式，实现遥测天线的自主稳定跟踪。当出现目标信号闪烁或者目标信号短暂丢失时，切换为数字引导方式，待信号稳定后重新切换为自动跟踪方式。在目标俯仰角度快到0度左右时，切换为手动跟踪方式，防止天线砸地现象发生。

由于差分解算可能存在的问题，数字引导的天线角度也可能与实时角度出现较大偏差。如图1所示，为使用MATLAB软件对某次伺服存盘文件进行数据处理，分别得到实时、数字引导与程序引导的天线方位角度曲线，和实时、数字引导与程序引导的俯仰角度曲线。在飞行时间180s~200s左右，数字引导的天线俯仰与方位角度均出现了明显的跳动，与实时角度和程序引导角度差别较大。此时如果天线设备使用的是数字引导跟踪方式，将会使天线产生剧烈抖动，同时丢失目标。

图1 实时、数字引导、程序引导三种方式的天线角度

下面计算数字引导方式下的电机转动瞬时速度。天线俯仰电机瞬时角速度E与方位电机瞬时角速度A的计算公式如下：

其中，1、2分别是时刻1、2的俯仰角度，1、2分别是时刻1、2的方位角度。计算数字引导跟踪方式的俯仰与方位的瞬时角速度，结果如表1所示。从图1、图2与表1中可以看出，在180.15s，数字引导的方位与俯仰角度均瞬间提高，瞬时角速度分别为514.56°/s和266.54°/s；在193.00s时刻，数字引导的方位与俯仰角度均瞬间减低，瞬时角速度分别为–2036.2°/s和256.64°/s；在180.60s，数字引导的方位瞬间提高，俯仰瞬间降低，瞬时角速度分别为1487.6°/s和–123.42°/s；在184.15s，数字引导的方位瞬间降低，俯仰瞬间提高，瞬时角速度分别为–777.18°/s和474.48°/s。如表2所示，天线方位电机的最大角速度为40°/s，俯仰电机的最大角速度为30°/s，可以看到，表1中所示时刻的方位角速度与俯仰角速度超过了电机的最大角速度。因此，如果在180s~200s这段时间内切换为数字引导跟踪方式，将会使天线设备产生剧烈抖动，造成设备的严重损伤，或者导致设备限位锁定，影响后续跟踪功能。鉴于数字引导的不稳定性，应该再着力提高记忆跟踪精度和长度，以便在跟踪时，一旦目标失锁，自跟踪失效，能够自动切换记忆跟踪，实现稳定持续的目标跟踪测量。

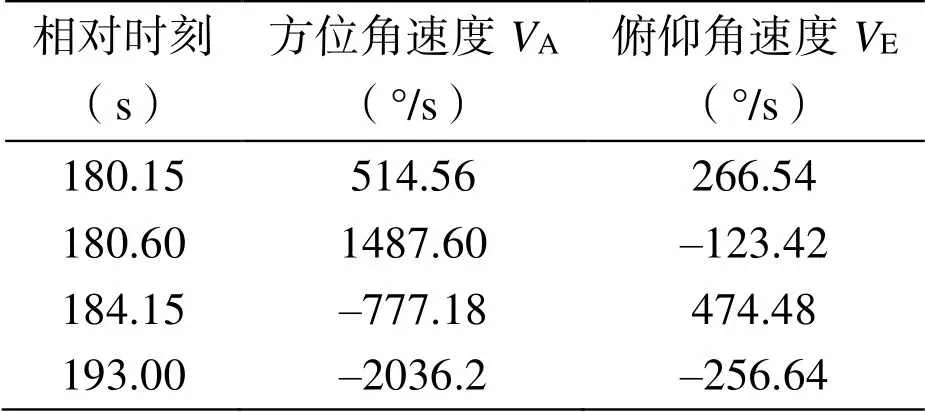
表1 俯仰与方位速度

表2 方位与俯仰电机最大角速度与角加速度

此外，由于测控目标有可能偏离理论弹道飞行，所以天线实时角度有可能与程序引导角度不完全一致。为了方便观察，把图1进行局部放大显示，显示结果如图2所示。从图2可以看到，在起飞初始段的60s~130s时间段内，实时方位、实时俯仰角度与理论弹道即程序引导方位、程序引导俯仰基本一致；在飞行接近末端的200s~400s时间段内，实时方位、实时俯仰角度与程序引导方位、程序引导俯仰有了一定的差别，这是因为飞行器在飞行过程中受到风速、燃料燃烧等客观因素影响导致飞行轨迹与理论弹道出现偏差，并且飞行时间越长，偏离理论弹道的可能性越大。不过，从图2中可以看到，偏离理论弹道的情况并不是很严重，基本上实时方位、俯仰与程序引导方位、俯仰角度的差别控制在1°以下。

图2 图1的局部时间显示

2 遥测天线自主跟踪稳定度

天线设备对测控目标实现稳定自跟踪，是遥测设备最常用、最基本的一种跟踪方式。天线设备自跟踪的稳定性直接影响遥测信号的接收性能与天线设备寿命。如果遥测跟踪天线出现剧烈抖动，或者出现长时间的轻微抖动，会降低馈源接收信号的稳定性与信噪比，且对天线电机设备造成一定的损害。使用MATLAB软件对某次存盘文件的实时方位与俯仰角度进行绘图处理，得到实时的方位角度曲线与实时的俯仰角度曲线，如图3所示。从图3可以看到，方位角度曲线与俯仰角度曲线都具有明显的振荡特征，尤其是俯仰角度曲线的上下波动较大，与实时角度曲线应具有较为光滑的特征要求不相一致。我们希望寻找一种方法，通过对存盘数据的实时角度曲线进行分析，来确定天线自主跟踪的稳定度，以衡量评价跟踪的效果。

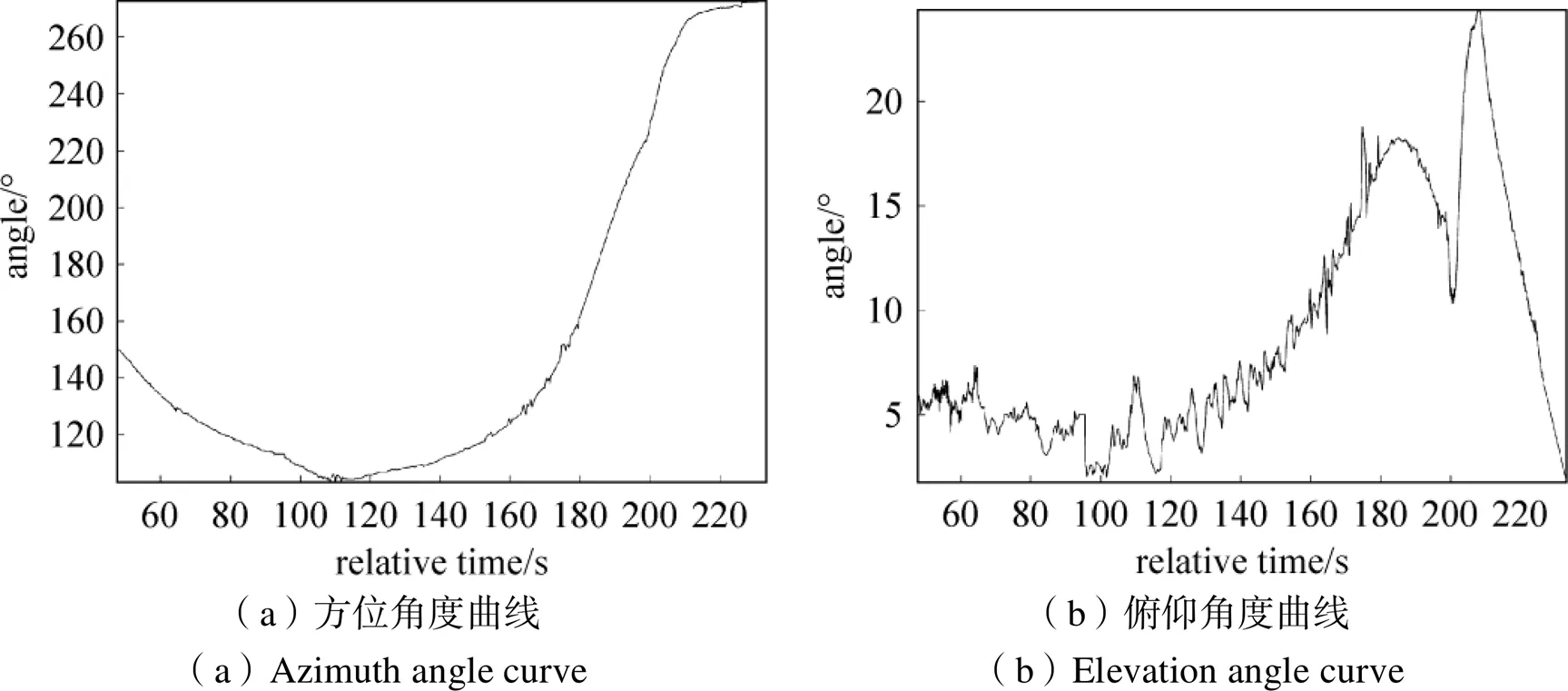
图3 实时角度曲线

2.1 变差分析方法

假设离散的实时方位角度值为[]，俯仰角度值为()，采样长度为，则方位曲线与俯仰曲线的变差计算公式如下所示：

其中，A、E分别为方位角度曲线与俯仰角度曲线的变差。变差方法也可以称为拐点法、左右差法，即如果一个采样点与左右两个采样值构成一组数据，且这个采样点是拐点，那么变差值则增加一。

2.2 方差分析方法

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望之间的偏离程度。在表示跟踪角度曲线时，方差越大表示曲线偏离均值的概率越大。

假设离散的实时方位角度值为[]，俯仰角度值为()，采样长度为，则方位曲线与俯仰曲线的方差计算公式如下所示：

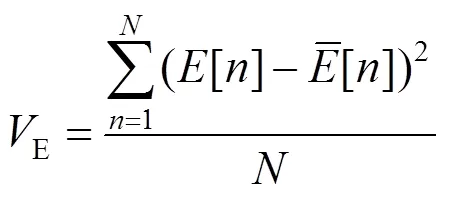
2.3 实验算例分析

通过实验分析表明，变差方法在衡量自主跟踪稳定度上具备有效性。如图4所示，为某次存盘数据的方位角度与俯仰角度曲线，包括实时角度、数字引导角度、程序引导角度三种数据。该数据采样间隔为0.05s，采样数为10510个，共525.5s。通过计算，得到的方位角度与俯仰角度结果分别示于表3、表4。

首先分析方位角度曲线的变差属性。从表3中可以看出，程序引导角度的变差最小，这是因为理论弹道比较稳定，曲线比较平滑，没有出现上下跳变的现象。同时，实时角度的变差最大，这是因为在实时跟踪过程中，实时的方位角度不够平滑，上下跳动较多，这不利于天线的稳定运转和信号的稳定接收。图5（a）所示为图4（a）的局部放大，可以看到，实时方位角度具有明显的上下跳动特征，与飞行器的方位角度稳定、单调变化特征不相符合。此外，数字引导方位角度的变差介于实时角度与程序引导角度的变差之间，即数字引导的方位角度稳定度比实时角度的稳定度更好，但不如程序引导方位角度的稳定度。从图5（a）可以看到，数字引导同样表现为不规则的上下跳动，且在156s~157s处出现了角度突变跳动的不正常情况。此外，计算图3所示数据的变差，方位角度曲线为2625，俯仰角度曲线为2933，二者的数值都较大，说明这次跟踪的实时跟踪天线稳定度不够，摆动现象较为突出。

图4 方位与俯仰角度曲线

表3 方位角度属性值

表4 俯仰角度属性值

图5 图4的局部放大

接下来分析俯仰角度曲线的变差属性，从表4可以看到，程序引导俯仰角度同样变差最小，表现为最稳定；而数字引导俯仰角度的变差最大，甚至超过了实时俯仰角度的变差，这说明数字引导俯仰角度不够稳定，从图5（b）中也可以看出数字引导俯仰角度具有明显的跳动。

接下来分析方位角度曲线与俯仰角度曲线的方差属性，如表3和表4所示。可以看到，方差相差不大，且无论是方位角度还是俯仰角度，数字引导的方差都比程序引导的方差大，这主要是因为数字引导在156s~157s附近出现了十分明显的异常跳变，导致出现了若干个偏离均值的绝对大值，最终导致方差较大。因此，曲线方差可以作为衡量跟踪曲线是否出现较明显异常跳动的一个参考属性。

3 结束语

本文使用MATLAB对遥测天线的跟踪记录数据进行绘图，并做了分析对比，得到了如何合理选择跟踪方式的结论。本文还提出了基于变差的遥测天线自主跟踪稳定度分析方法，并通过MATLAB实验进行验证，得出了跟踪曲线变差越大，稳定度越差的结论。本文还提出了基于方差的明显异常跳动检测方法，即方差越大，异常跳动越明显。本文的研究内容和结论对于使用遥测记录数据，衡量遥测天线跟踪质量，改善跟踪方式提供了有效的参考。

[1] 周智敏, 李企舜. 现代航天测控原理[M]. 长沙: 国防科技大学出版社, 1988.

[2] 丁镇生. 传感及其遥控遥测技术应用[M]. 北京: 电子工业出版社, 2003.

[3] 李筱雅. 多目标综合遥测监控系统架构设计[J]. 现代电子技术, 2012, 35(20): 124–127. LI Xiaoya. Design of multi-target comprehensive telemetry monitoring system architecture[J]. Modern Electronics Technique, 2012, 35(20): 124–127.

[4] LI Bingchang. Development of china′s space telemetry technology[J]. Aerospace China, 2009, 10(3): 17–19.

[5] BARRY MATTHEW R, SCOTT KEVIN L, WEISMULLER STEVEN P. A distributed computing model for telemetry data processing[J]. Robotics and Computer-Integrated Manufacturing, 1994, 11(2): 99–104.

[6] 李民生, 姚珍榕. 遥测程控跟踪天线系统[J]. 遥测遥控, 1991(3): 24–27.

[7] 于志坚, 房鸿瑞. 对我国遥测技术发展的思考[J]. 遥测遥控, 2003(5): 1–8,29.

[8] 常青, 李显旭, 何善宝. 我国空间信息网发展探讨[J]. 遥测遥控, 2015, 36(1): 1–10. CHANG Qing, LI Xianxu, HE Shanbao. Confer on the evolution of earth-space integrated information network of China[J]. Journal of Telemetry, Tracking and Command, 2015, 36(1): 1–10.

[9] UGLOW K. Multiplex telemetry modulation and demodulation methods[J]. IEEE Transactions on Communication Technology, 2003, 16(1): 133–141.

[10] 孔冬. 高速PCM/FM遥测解调技术研究[D]. 成都: 电子科技大学, 2012.

[11] 庞岳峰, 李娟, 褚福勇. 基于小波分析的遥测设备角误差信号降噪研究[J]. 遥测遥控, 2014, 35(6): 38–44,49. PANG Yuefeng, LI Juan, CHU Fuyong. Research on angle error signal denoising in telemetry equipment based on wavelet analysis[J]. Journal of Telemetry, Tracking and Command, 2014, 35(6): 38–44,49.

[12] 张娜, 刘颖, 付庆勇, 等. 飞行器遥测跟踪的多模式自动转换方法研究[J]. 遥测遥控, 2019, 40(1): 61–66.ZHANG Na, LIU Ying, FU Qingyong, et al. Research on multi-mode automatic switching method in aircraft telemetry tracking[J]. Journal of Telemetry, Tracking and Command, 2019, 40(1): 61–66.

[13] MATTIELLO S. Management of wild fauna,utilization of telemetry tracking[J]. Journal of Comparative Pathology, 2000, 78(4): 477–487.

[14] 朱雪萍. 遥测设备的低仰角跟踪技术[J]. 无线电工程, 2003(1): 32–34.

[15] 张云昆, 张龙. 导弹对空中目标毁伤的坐标系转换方法及应用[J]. 四川兵工学报, 2012, 33(2): 18–19.

Research on tracking stability of telemetry antenna based on variation

CHEN Jianyou, PANG Yuefeng, LIU Jinjin, XIE Kejia

（Jiuquan Satellite Launch Center, Jiuquan 732750, China）

This paper deals with servo tracking data of telemetry system, analyzes and compares several tracking methods, points out the possible problems in several tracking methods, and puts forward corresponding improvement measures. The stability and jump degree of antenna azimuth and elevation angle during autonomous tracking are studied through the attribute analysis of curve variation and variance. We analyze and compare with the curve stability of theoretical trajectory and digital guidance. The conclusion is that the greater the variation, the worse the stability, and the bigger the variance, the more obvious the abnormal jump.

Telemetry antenna; Autonomous tracking; Curve stability; Curve variation

TP391.9

A

CN11-1780(2020)01-0059-07

Email:ycyk704@163.com

TEL:010-68382327 010-68382557

酒泉卫星发射中心科研基金项目（2018ZKZ003）

2019-08-29

陈建友 1989年出生，硕士，工程师，主要研究方向为航天遥测遥控。

庞岳峰 1980年出生，硕士，工程师，主要研究方向为无线电遥测技术。

刘津津 1994年出生，本科，助理工程师，主要研究方向为通信工程。

谢克佳 1995年出生，本科，助理工程师，主要研究方向为无线电测量。