最优频移小波包变换窄带干扰抑制方法研究

章兰英

最优频移小波包变换窄带干扰抑制方法研究

章兰英

（航天工程大学士官学校 北京 102249）

针对频移小波包变换不能抑制多音干扰的问题，提出了基于遗传算法最优频移小波包变换的窄带干扰抑制方法。采用遗传算法进行频移和分解层数的最优选择，并采用奇偶判断的方法进行自适应小波包分解。仿真结果表明，该方法能够有效抑制窄带干扰。

窄带干扰抑制；小波包变换；遗传算法；奇偶判断

引 言

测控设备处于纷繁复杂的电磁环境中，面临的各种干扰日益严重。虽然扩频测控系统具有很强的窄带干扰抑制能力，但是当干扰功率超过一定容限时，系统性能将会明显下降，因此在实际应用中，必须采取一定的信号处理手段来增强系统的抗强干扰能力。

常用的窄带干扰抑制方法有时域处理技术[1]和变换域处理技术[2-4]，其中小波包变换灵活的局部时频分析能力可以有效地抑制窄带干扰[5-8]，但是当干扰频率位于小波包分解的两个子带之间时，干扰将不能彻底滤除。为了解决上述问题，文献[9]提出了频移非抽取性小波包变换算法SUWPTA（Shifted Undecimated Wavelet Packet Transform Algorithm），通过将干扰频移至子带中间来确保彻底抑制干扰，但是SUWPTA只能抑制单个的窄带干扰，而对于多音干扰，SUWPTA将无法抑制。针对SUWPTA不能抑制多音干扰的问题，本文研究了基于遗传算法最优频移小波包变换的窄带干扰抑制方法。首先采用遗传算法对频移和最高分解层数进行最优选择，然后通过奇偶判断，实现信号自适应小波包变换和重构，最后通过仿真验证了该方法能够有效实现窄带干扰的抑制。

1 基于SUWPTA的窄带干扰抑制原理

基于SUWPTA的窄带干扰抑制方法是通过在分解的最高层将干扰频移至最近的子带中间，然后从最高层向最低层分解，直至将干扰移至第一层的某个子带中间，再将含干扰子带置零，最后根据各层的频移量和各子带分量重构信号达到干扰抑制的目的。

假设小波包分解的最高层为，其对应的子带带宽为B，需要进行次频移来搜索最优频移量()。最优频移搜索过程如图1所示。

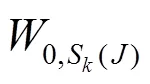
文献[9]提出采用子带能量差最大来选择最优频移，当子带能量差最大时，干扰位于子带中间，此时对应的频移量为最优频移量，即

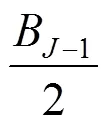
对于单个的窄带干扰，SUWPTA可以通过子带能量差最大准则将窄带干扰频移至子带中间。但是，当窄带干扰为多音干扰，子带能量差最大时，干扰并不是完全位于子带中间位置，因此，SUWPTA无法抑制多音干扰。

2 基于遗传算法最优频移小波包变换的窄带干扰抑制方法

为了解决SUWPTA无法抑制多音干扰的问题，本文提出了基于遗传算法GA（Genetic Algorithms）最优频移小波包变换的窄带干扰抑制方法，其流程如图2所示。

图2 基于遗传算法最优频移小波包变换的窄带干扰抑制流程

具体步骤如下：

① 正交下变频

对接收到的中频信号()进行正交下变频，得到基带复信号()

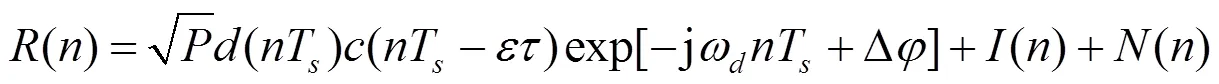
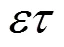
② 确定最优分解层数和最优频移量()

采用遗传算法确定最优分解层数和最优频移量()，以使()中的干扰能够移至第层的子带中间。

③ 自适应小波包分解

根据最优频移量()得到频移后的信号R(J)()。

对R(J)()进行自适应小波包分解，保存各向量及频移量，以备重构。

④ 窄带干扰抑制

将存在干扰的子带置零，以滤除干扰。

⑤ 自适应小波包重构

下面重点对最优分解层数和最优频移量()的选择，以及自适应小波包分解这两个问题进行分析。

2.1 基于遗传算法的最优频移和分解层数选择

为了能够确保频移后的多音干扰能够位于子带中间位置，可以采用遗传算法对最高分解层数和频移两个参数均进行最优选取。

GA的基本流程如图3所示。

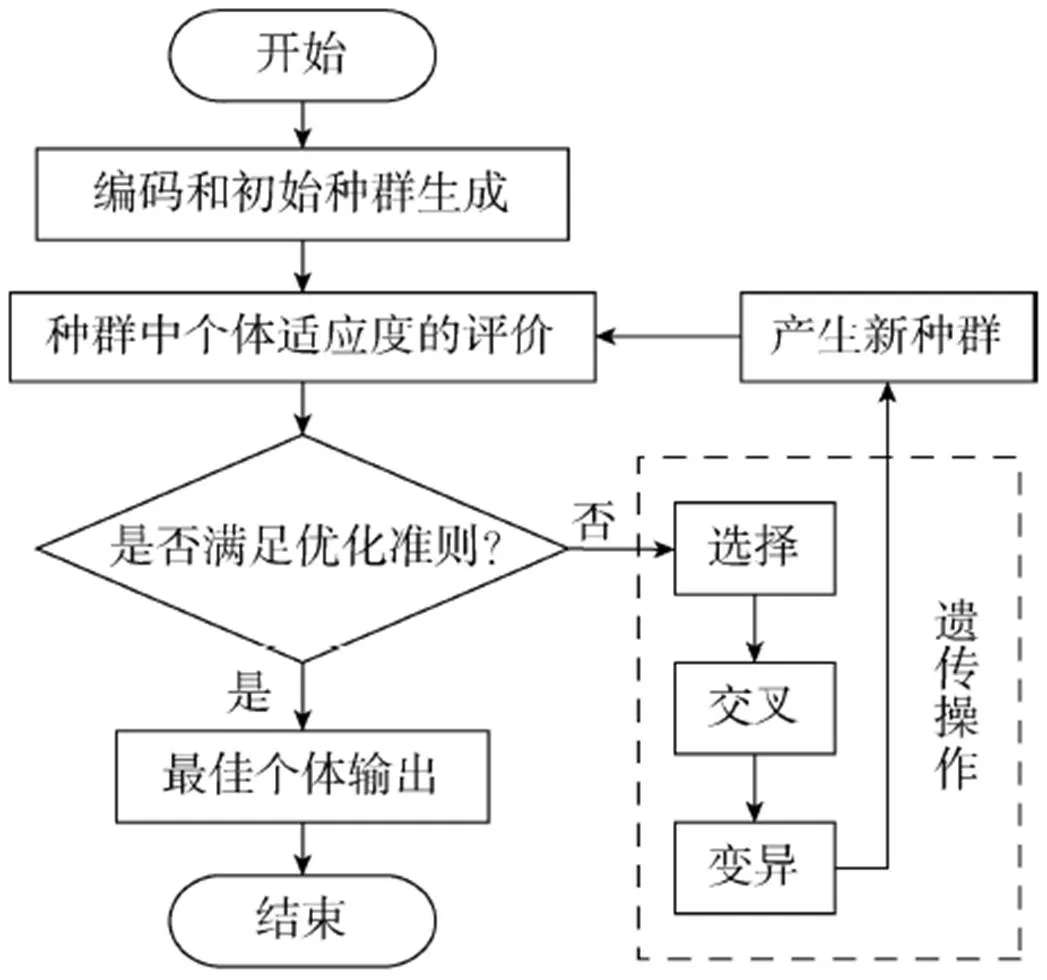
图3 遗传算法流程图

由图3可以看出，遗传算法主要包含参数编码、初始种群生成、适应度函数设计、遗传操作设计、控制参数设定、算法终止条件设置等6个基本要素，其中遗传操作包括选择（selection）、交叉（crossover）和变异（mutation）3个主要操作算子。下面主要对参数编码、适应度函数设计和遗传操作设计等3个要素进行分析和设计。

2.1.1 参数编码

本文涉及到寻找最优频移和最优分解层数两个变量的最优解，对两个决策变量的个体进行编码时需要采用多参数级联编码方式。

首先分析频移量编码。频移量的区间长度为B，仿真表明频移量的求解精确到B/24即可满足要求，综合考虑求解精度和算法的复杂度，频移量编码可以采用二进制编码，且二进制串长度为4。

其次分析最高分解层数编码。最高分解层数是一个正整数，它的取值不能太小，否则在滤除干扰时对有用信号的损害也较大，引起信号失真，的取值也不能太大，否则窄带干扰将不能完全位于一个子带内，而造成干扰抑制不完全。综合考虑设定的取值范围为[5，12]。因此可以采用长度为3的二进制编码。

最后将上述两个编码连接组成双参数级联编码，作为遗传算法的输入参数。

2.1.2 适应度函数的设计

经仿真发现，当干扰位于子带中间位置时，对信号进行小量频移时的子带能量是平稳变化的，如图4所示。

图4中第5~10个频移步进时，干扰位于子带中间位置，对应的子带能量差变化平稳，而当干扰位于子带边缘位置时，由于子带滤波器对信号幅度的影响较大，子带能量变化波动较大，如图4中第11~20个频移步进时对应的子带能量差变化波动较大。因此可以采用子带能量差平稳度来选择最优频移和最佳分解层数。子带能量差平稳度函数定义为

本文采用子带能量差平稳度函数作为本文的目标函数，目标函数越大，说明此时有干扰位于子带交界处，子带能量越不平稳，个体的性能也越差，被选择的机会也越小。

图4 子带能量变化

根据适应度函数的特点，直接将目标函数转化为适应度函数（fitness function）

2.1.3 遗传操作设计

① 选择

选择的目的是为了从当前种群中选出优良的用于进行交叉操作的个体。群体中每个个体的选择概率取决于群体中个体的适应度及其分布，因此选择操作的第一步是计算适应度。本文中个体选择概率的分配方法采用基于排序的适应度分配，种群按目标值进行排序，适应度取决于个体在种群中的序位。采用线性排序的个体适应度如下：

其中，为个体在种群中的序位，为选择压力，为种群大小。

则个体的选择概率为

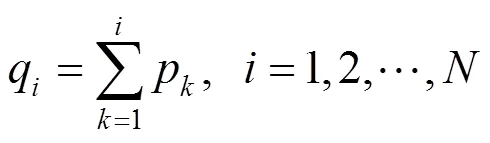
重复步骤上述步骤次，可得个复制的个体。

② 交叉

由于本文中参数采用的是二进制编码，因此交叉操作采用单点交叉的基因重组方式。

被选中的两个父代个体按照设定的概率进行交叉操作产生两个子代个体，单点交叉示意如图5所示。

③变异

变异是指将个体染色体编码串中的某些基因座上的基因值用该基因座的其他等位基因来替换，从而形成一个新的个体。对于二进制编码的个体而言，变异就是把某些基因座上的基因值进行翻转。

图5 单点交叉

2.1.4 算法流程

基于遗传算法的最优频移和最优分解层数选择流程如下：

① 参数编码：根据频移和分解层数的取值范围进行二进制编码，然后将两个编码连接组成双参数级联编码，作为遗传算法的输入参数；

② 初始种群产生：随机生成个个体，形成初始的染色体群体；

③选择：计算群体中个体的适应度及选择概率，然后根据个体选择概率采用RWS选择出对染色体作为父代个体；

④ 交叉：按照一定的交叉概率对选择出的父代个体进行单点交叉，得到新的个体；

⑤ 变异：按照一定的变异概率对交叉后的个体进行变异操作，形成新的子代个体；

⑥ 终止：若满足终止条件，则此时适应度最大的个体即为最优解，通过解码得到最优频移和最优最高分解层数，否则返回步骤②。

2.2 基于奇偶判断的自适应小波包分解树

通过子带能量差平稳度获得最优频移量后，各NBI分别位于不同的子带中间。当信号中存在多个干扰时，如果左右节点都存在干扰时，将不能通过子带能量大小来确定子节点是否继续分解，为了便于小波包分解，本文提出了基于奇偶判断的自适应小波包分解树。

首先对各层子带进行编号，编号方式如图6所示。

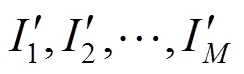
式（12）中，矩阵的第1行表示在=6层时含干扰的子带编号，第2行表示在=5层时含干扰的子带编号，以此类推，直到第6行表示在=1层时含干扰的子带编号。根据中各数的奇偶性得到干扰频带变化矩阵。

其中，0表示奇数，说明干扰位于低频子带，1表示偶数，说明干扰位于高频子带，中每一列表示，在小波包分解过程中1根干扰在高、低频子带之间的变化情况，由此可以得到与对应的小波包分解树如图7所示。

图7中，最后一层中的△表明该子带存在干扰，其中的序号与中列的序号相对应。因此，通过对干扰子带编号的奇偶性判断可以很容易得到小波包的自适应分解树。

图6 子带编号示意图

3 窄带干扰抑制性能仿真分析

下面仿真窄带干扰抑制性能，主要比较本文提出的基于遗传算法最优频移小波包变换的窄带干扰抑制方法（以下简称GA算法）和文献[9] E. Pardo提出的窄带干扰抑制方法（以下简称EP算法）这两种算法的干扰抑制性能。

系统参数：采样率56Msps，载波中心频率70MHz，PN码为长1023的gold序列，PN码速率5.115Mcps，信息码速率5kbps，信干比SIR=–40dB，载噪比52dBHz。

干扰参数：单音干扰频率为0.1386π，多音干扰频率为[–0.0352π，0.0294π，0.3177π]，窄带AR干扰采用极点为0.99的二阶AR过程。

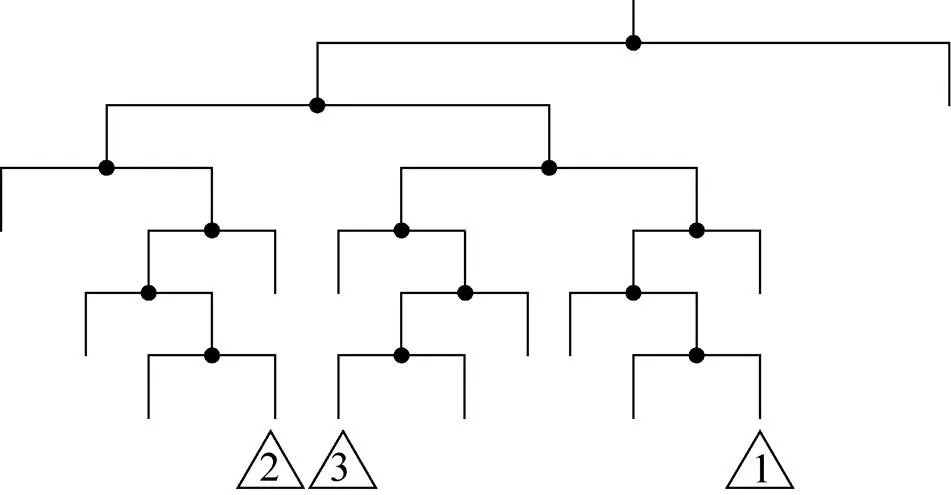
图7 小波包分解树

3.1 频移参数选择仿真

首先仿真比较采用遗传算法和子带能量差最大法对最优频移和最优分解层数的选择结果，其中，EP算法的最优分解层数根据遗传算法的选择结果设定，为了较好地显示频移结果，下列图中信号频谱幅度分别除以2×106。

3.1.1 单音干扰

遗传算法选择结果：=7，()=109.375kHz，EP算法选择结果：′=7，′()=27.344kHz。信号频移后的频谱如图8所示。

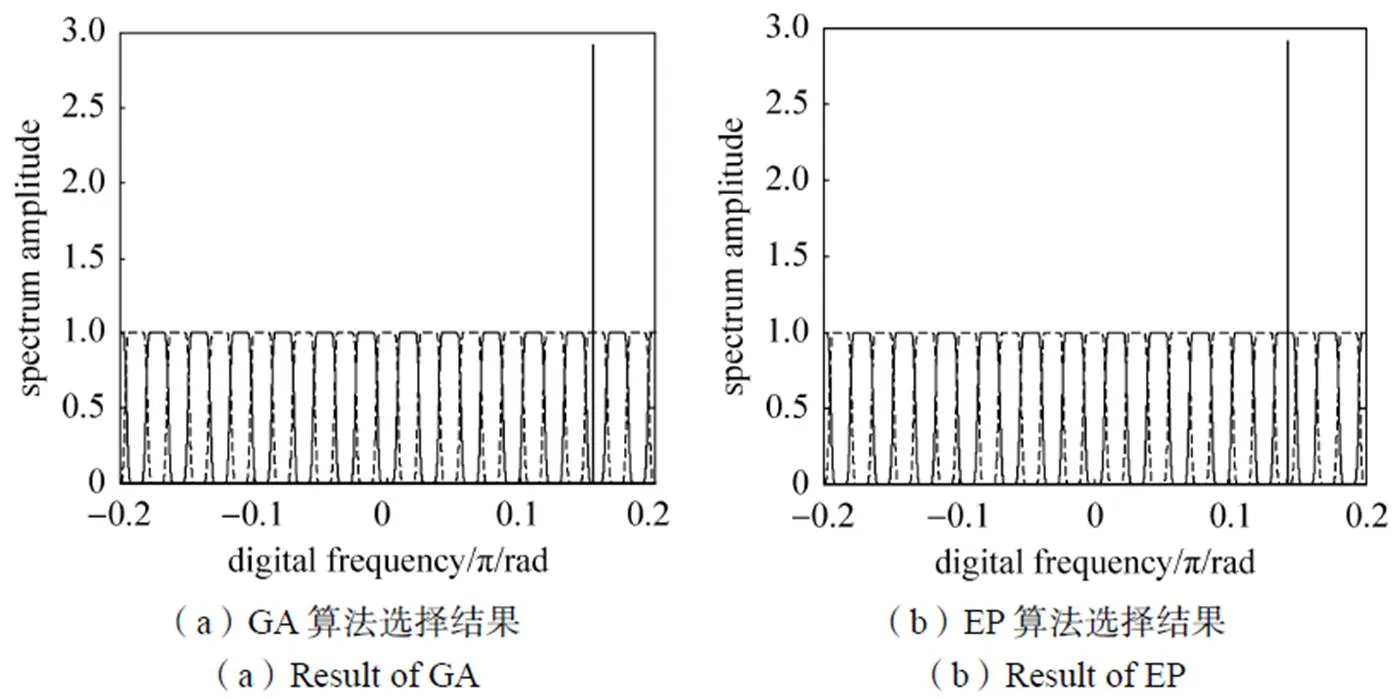
图8 单音干扰频移后的频谱

由图8可以看出，频移后的单音干扰均位于小波包子带中间。

3.1.2 多音干扰

遗传算法选择结果：=6，()=7.0565kHz，EP算法选择结果：′=6，′()=98.438kHz。信号频移后的频谱如图9所示。

图9 多音干扰频移后的频谱

由图9可以看出，GA算法将3根干扰频移后分别位于不同的子带中间，而EP算法为了获得最大的子带能量差，将3根干扰频移后均位于高频子带边缘。

3.1.3 窄带AR干扰

遗传算法选择结果：=5，()=0kHz，EP算法选择结果：′=5，′()=437.5kHz。信号频移后的频谱如图10所示。

图10 窄带AR干扰频移后的频谱

由图10可以看出，频移后的窄带AR干扰均位于小波包子带中间。

通过以上仿真可以看出，GA算法能够自适应选择最优频移和最优分解层数，以确保窄带干扰均位于子带中间位置，而EP算法在多音干扰情况下根据子带能量差最大的原则不能将干扰移至子带中间位置。但是另一方面，由于GA算法需要通过遗传算法进行最优解的选取，因此算法的复杂度和运算量都比EP算法有所增加。

3.2 误码率仿真分析

下面仿真不同干扰下的误码率，误码率统计信息码元个数为105，载噪比变化范围40dBHz~ 50dBHz，对应解扩后信噪比变化范围0dB~10dB。下列图中理论值为不存在干扰情况下，对BPSK进行相干解调的理论误码率值。

三种干扰情况下，干扰抑制后的解调误码率曲线如图11所示。

图11 干扰抑制后的误码率曲线比较

由图11可以看出，单音干扰和窄带AR干扰下，GA算法和EP算法的误码率相差不大，并且单音干扰时的误码率要低于窄带AR干扰时的误码率。而多音干扰情况下，GA算法仍然可以正确解调信号，且误码率比单音和AR干扰的误码率要大，这是因为多音干扰占用的子带较多，采用小波包变换滤除干扰时对信号有用部分的损失较多，因此误码率有所增大。EP算法的误码率在多音干扰下很大，基本无法正确解调。

4 结束语

针对SUWPTA无法抑制多音干扰的问题，提出了基于遗传算法最优频移小波包变换的窄带干扰抑制方法，首先采用遗传算法对频移和最高分解层数进行最优选择，然后通过对含干扰的子带编号进行奇偶判断，得到自适应的小波包分解树，并根据分解树对信号进行自适应小波包变换，在最低层抑制干扰，最后对干扰抑制后的信号进行重构。仿真结果表明，该方法不仅能够抑制单音干扰和窄带AR干扰，也能够有效抑制多音干扰。

[1] 刘泳庆, 邵晓田, 李一品, 等. 基于内插型双边带滤波器的时域自适应滤波[J]. 北京理工大学学报, 2016, 36(10): 1085–1088. LIU Yongqing, SHAO Xiaotian, LI Yipin, et al. Time-domain adaptive filtering algorithm based on interpolating transversal filter with two-sided taps[J]. Transactions of Beijing Institute of Technology, 2016, 36(10): 1085–1088.

[2] 胡旭东, 张成文, 刘玉涛, 等. 面向OFDM系统的高精度窄带干扰抑制算法[J]. 西安交通大学学报, 2019, 53(8): 114–120. HU Xudong, ZHANG Chengwen, LIU Yutao, et al. A high precision suppression algorithm of narrowband interferences for OFDM systems[J]. Journal of Xi’an Jiaotong University, 2019, 53(8): 114–120.

[3] 马千里, 肖卓, 宋志群. OFDM系统中的窄带干扰抑制[J]. 计算机测量与控制, 2018, 26(10): 150–154. MA Qianli, XIAO Zhuo, SONG Zhiqun. Narrowband interference suppression in OFDM system[J]. Computer Measurement & Control, 2018, 26(10): 150–154.

[4] WANG Lan, YANGYuhong, LIPengxu, et al. Multi-tone interference suppression in DSSS system based on the optimal frequency shift of undecimated wavelet packets[J]. IEEE International Conference on Communications Software and Networks, 2016: 316–319.

[5] ANGRISANI L. A wavelet packet transform-based approach for interference measurement in spread spectrum wireless communication systems[J]. IEEE Trans on Instrumentation and Measurement, 2005, 54(6): 2272–2280.

[6] 陆丹丹, 朱立东. 调频通信系统的盲窄带干扰抑制算法[J]. 无线电通信技术, 2016, 42(1): 18–20, 42. LU Dandan, ZHU Lidong. Research on blind narrowband interference suppression algorithm based on FHSS[J]. Radio Communication Technology, 2016, 42(1): 18–20, 42.

[7] 孟生云, 杨文革, 王东辉. 基于双重判断策略的自适应WPT窄带干扰抑制方法[J]. 遥测遥控, 2013, 34(4): 46–52. MENG Shengyun, YANG Wenge, WANG Donghui. Narrowband jamming suppression method based on adaptive WPT with double judgement strategy[J]. Journal of Telemetry, Tracking and Command, 2013, 34(4): 46–52.

[8] 乔晓斌, 张友爱, 缪学宁. 基于小波包变换的DSSS窄带干扰抑制算法研究[J]. 舰船电子工程, 2007, 159(3): 80–82, 218. QIAO Xiaobin, ZHANG Youai, MIU Xuening. Narrowband interference excision for DSSS communication system using wavelet packet transform[J]. Ship Electronic Engineering, 2007, 159(3): 80–82, 218.

[9] PARDO E, RODRIGUEZ M A, PEREZ J J. Narrowband interference suppression using undecimated wavelet packets in direct-sequence spread-spectrum receivers[J]. IEEE Trans on Signal Processing, 2006, 54(9): 3648–3653.

Research on the narrowband interference suppression method based on optimal frequency shift WPT

ZHANG Lanying

（NCO school, Space Engineering University, Beijing 102249, China）

For the multi-tone interference could not be suppressed by shift WPT, the narrowband interference suppression method based on genetic algorithm optimal frequency shift WPT was proposed. Genetic algorithm was adopted to choose the optimal frequency shift and the highest frequency resolution level. And the adaptive WPT decomposition method based on parity checking was presented. Simulation results show that this algorithm can suppress NBI interference effectively.

Narrowband interference suppression; Wavelet packet transform; Genetic algorithm; Parity checking

TN974

A

CN11-1780(2020)01-0026-08

2019-07-04

Email:ycyk704@163.com

TEL:010-68382327 010-68382557

章兰英 1981年生，博士，讲师，主要研究方向为航天测发测控、信号处理。