处理双变量问题的常见策略

广东省东莞市东莞实验中学 尹淑芬

双变量问题活跃于高考题和竞赛题中,问题形式多样,出现在选择填空题,也出现在压轴题中.这类问题难度大,综合性强,问题的求解对学生思维能力要求高.本文将结合例题说明处理双变量问题的常见三大策略,为学生解决该类问题提供有效的路径.

策略一 消元

(一)换元法

常见换元有两种:整体换元与三角换元.

(1)整体换元若双变量表达式可以通过变形,能够把一个含有双变量的式子视为一个整体,那么可以通过换元转化为单变量表达式,常见的如等.

例1(2019年清华大学自主招生考试第11 题)实数x,y满足x2+(y −2)2≤1,求的最大值和最小值.

解答当x= 0 时,当0 时,当x>0 时,易得令

当x <0 时,易得令,θ ∈

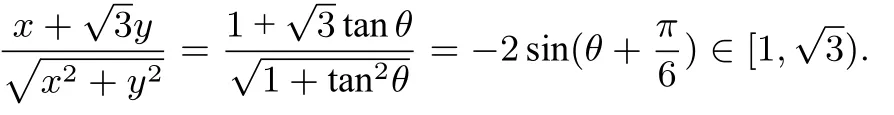
评注通过齐次化,构造出,使用整体换元法,减少变量,在此过程中需要求出元的取值范围.

(2)三角换元当已知条件为关于两个变量x,y的齐次式之和或之差等于一个确定的常数,可以联想到三角公式,从而把两个变量x,y的表达式转化为三角函数表达式来求出范围.

常见的三角换元有:

如果条件中有x2+y2= 1 可作代换为x= cosθ,y=sinθ.

如果条件中有x2−y2= 1 可作代换为x= secθ,y=tanθ.

例2已知x2+y2=4,求|x2+2xy −y2|的最大值.

解答设x=2 cosθ,y=2 sinθ,θ ∈[0,2π),所以|x2+2xy −y2|的最大值为

评注三角函数公式变形比多项式变形更为丰富,若使用三角换元,便可以使用三角函数的各种恒等式进行变形,实现对代数式的简化.

(二)主元法

例3证明:

证明不妨设a > b,则待证不等式变成(lna −lnb)(a+b)−2(a −b)>0.把a看作是变量,b看作是常数,构造函数f(a)=(lna −lnb)(a+b)−2(a −b),a>b.在(b,+∞)上单调递增,f′(a)> f′(b)= 0,所以f(a)在(b,+∞)上单调递增,f(a)>f(b)=0,不等式得证.

评注当两个变量相互独立,可以以其中一个变量为“主元”,另外一个变量为常数,构造出以“主元”为自变量的函数,结合函数的基本性质解题.若两个变量的取值相互影响,那就不适宜使用主元法.

(三)利用等量关系消元

若出现两个变量之间的关系等式,则可以利用等式进行消元,减少变量的个数,在消元的过程中需要注意求出留下的变量的取值范围.

例4(2018年高考全国I 卷理科)已知函数f(x)=

(1)讨论f(x)的单调性;

(2)若函数f(x)存在两个极值点x1,x2,证明

解答(1)略.(2)由知x1x2=1,不妨设0(a −2)(x1−x2),即

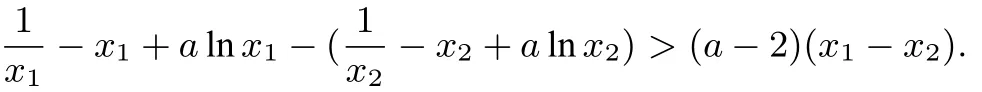
评注要证明的不等式,涉及到两个变量.导函数有两个不同实数根x1,x2利用韦达定理,我们得到了两个变量x1,x2的关系,把x2用关于x1的代数式表示出来,即代入到待证的不等式中,便可把双变量不等式化为单变量不等式,难度下降.

策略二 放缩

例5(2014年高考辽宁卷理科第16 题)对于c >0,当非零实数a,b满足4a2−2ab+4b2−c=0 且使|2a+b|最大时,的最小值为____.

解答由4a2−2ab+4b2−c=0 得

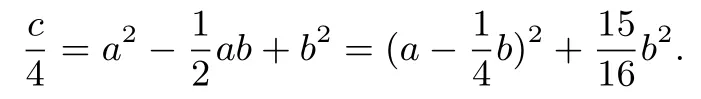
由柯西不等式得

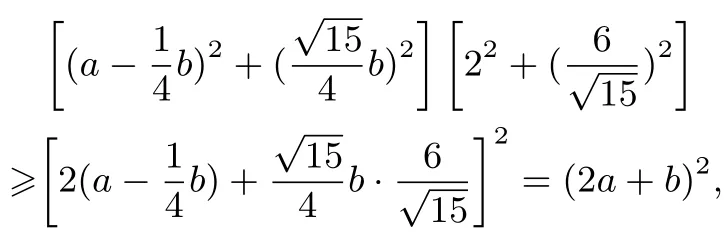
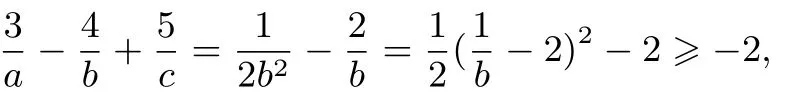
评注学生已经学习了均值不等式和柯西不等式,求双变量代数式的最值,可以尝试把该代数式配凑出学生已经学习过的不等式的形式.

策略三 数形结合

把涉及到双变量的表达式“翻译”为几何条件,转化为线性规划问题,利用几何的直观性,得知双变量的取值范围.

例6(2017年高考浙江卷第15 题)已知向量a,b满足|a|=1,|b|=2,求|a+b|+|a −b|的最大值和最小值.

解答设|a+b|=x,|a−b|=y,由已知条件,得x2+y2=10,x,y ∈[1,3],|a+b|+|a −b|的最值就是x+y的最值,这就转变成为一个线性规划问题:直线l:x+y=z与圆弧x2+y2= 10,x,y ∈[1,3]有交点,求直线l的纵截距z的最值.

通过图像,可以得知当直线l与圆弧相交于点(1,3),(3,1)时,纵截距z取最小值4.直线l与圆弧只有一个交点时,纵截距z取最大值所以,|a+b|+|a −b|的最小值和最大值分别为4 和

评注若能挖掘出题目中双变量限制条件所代表的几何信息,便可以充分利用几何的直观,实现难度降低.

双变量问题题型多变,难度大,对学生的思维水平要求高,本文总结了处理双变量问题的常见三大策略,希望能给学生提供解题思路指引,也希望能给一线教师一些启发.