ARIMA-SVR组合模型在基于标准化降水指数干旱预测中的应用

许德合，张 棋，黄会平

(1.华北水利水电大学地球科学与工程学院，河南郑州450000;2.华北水利水电大学测绘与地理信息学院，河南郑州450000)

旱灾被认为是世界上最严重的自然灾害类型之一［1］，极大程度地影响了人们的日常生活以及农业产量［2］。干旱是指水分收支或供求不平衡形成的水分短缺现象［3］，全球气候变暖、碳排放量超标等问题将加剧未来农业干旱情况，严重威胁全球粮食生产，因此准确评估、监测、分析干旱情况一直是国内外学者的热门话题［4］。对干旱进行量化研究有助于研究干旱时空变化特征，提升干旱监测能力，开展干旱预报工作，寻求干旱治理及应对策略，对未来我国农业生产以及防旱抗旱等方面具有重要意义［5］。我们通常选用便于计算的干旱指标来监测评估干旱发生的强度、持续时间和受灾范围［6］。由于干旱指标种类多、运用范围广，且不同专业和学科对干旱理解不同，因此出现了多种干旱指标［7］。标准化降水蒸散指数(Standard Precipitation Evaporation Index，SPEI)、帕默尔干旱指数(Plamer Drought Severity Index，PDSI)、降雨Z指数(ZIndex)、标准化降水指数 (Standard Precipitation Index，SPI)、综合干旱指数(Colligation Drought Index，CI)等在气象干旱、农业干旱、水文干旱等领域已得到广泛应用［8-12］。其中，SPI是用于表征某时段降水量出现概率多少的指标，计算结果对干旱分级精度相对较高，所需源数据少(仅利用日或月降水量数据就可进行计算)，适用范围广，并且不同时间尺度的SPI值可以适用于不同类型的干旱。由于该指标使用灵活，易于计算，已成为实际应用最广泛且适用于所有气候状况的干旱指标［13-16］。

加强干旱预测方面的研究对相关部门预防干旱灾害、减少干旱损失具有重要意义［17］。常用来预测干旱的模型有很多，如人工神经网络(Artificial Neural Network，ANN)、支持向量机(Support Vector Machine，SVM)和差分自回归移动平均模型(Autoregressive Integrated Moving Average，ARIMA)等。其中ARIMA模型是时间序列中常用的模型，通常用来预测线性数据;SVM模型是一种二分类模型，通常用来处理非线性数据;支持向量回归机(Support Vector Regression，SVR)是SVM的一种拓展，多用来进行非线性数据的回归预测，而ARIMA与SVR组合模型分别对线性模型及非线性模型处理具有优势，所以它们之间存在优势互补［18］。

河南省位于中国中部和黄河中、下游，是中国重要的粮食作物产区和农业大省，对于保障国家粮食安全发挥着至关重要的作用［19］。本研究以河南省国家级气象观测站郑州站为例，计算不同时间尺度的SPI值，利用ARIMA模型及ARIMA-SVR组合模型对其进行预测，并采用均方根误差(Root Mean Squared Error，RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)对 2种模型预测能力进行分析。

1 研究方法

1.1 SPI的计算

降水量通常是一种偏态分布，常采用Γ分布概率描述降水量的变化，再将偏态概率分布进行正态标准化处理，最后用标准化降水累计频率分布划分干旱等级［20-22］。SPI可以定量化研究多时间尺度的降水量不足。

SPI指数公式为［23-24］:

式中，Y(x)2为与Γ函数相关的降水量分布概率;x为样本值(即降水量);G为正负系数;u0、u1、u2和l1、l2、l3为常数:

当Y(x)＞0.5时，G=1，当Y(x)≤0.5时，G=-1。

Y(x)由Γ函数求得，其中Γ为概率密度积分公式:

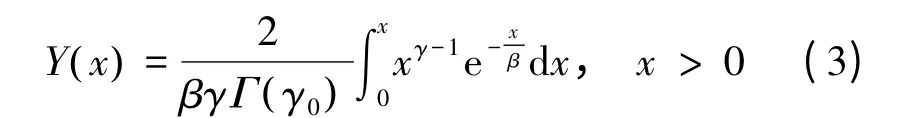
式中，γ，β为Γ分布函数的形状和尺度参数。

1.2 ARIMA模型

ARIMA分为自回归模型(Autoregressive model，AR)、滑动平均模型(Moving average model，MA)以及自回归移动平均模型(Autoregressive Moving Average Model，ARMA)，是传统的时间序列预测模型。其建模流程是首先判断模型平稳程度，其次利用差分法对非平稳时间序列进行平稳化处理，然后选取AR(p)，MA(q)对模型进行定阶，差分次数记为d，ARIMA(p，d，q)模型就是经过了d阶差分后的ARMA(p，q)模型。如下式所示［25］:

式中，φ(L)和θ(L)分别为:

ARIMA(p，d，q)模型的一般式:

上式中，d为差分次数，Δ=1-L，(φ1，φ2，…，φp)为自回归系数，p为自回归阶数，(θ1，θ2，…，θp)为移动平均系数;ut为白噪声序列(服从0均值、正态分布且相互独立的白噪声序列)。

其中p、q阶数采用赤池信息准则(Akaike Information Criterion，AIC)和贝叶斯信息准则(Bayesian Information Criterion，BIC)来确定，当样本数N固定时，选择AIC和BIC最小值来确定p，q。公式如下:

1.3 SVR模型

SVR模型是SVM的推广，SVR的本质属性不再是原来的二分类方法，而是回归方法。由于SVR模型在对非线性数据预测方面具有优势，因此采用ARIMA模型对线性数据SPI进行预测，将所得残差(非线性数据)传入SVR模型，再利用SVR模型对残差进行预测。通过引入径向基核函数(RBF)来把训练样本映射到高维空间下来进行回归预测，再将回归问题转为优化问题［26-28］:

式中，w为权重系数为松弛变量，规定了模型的误差要求;C为惩罚参数，C越大则支持向量的决策边界越大;b为偏置项。RBF公式中σ和γ关系如下:

1.4 ARIMA-SVR组合模型

由于ARIMA模型和SVR模型在线性和非线性预测中各有优点，因此本文分别采用 ARIMA与SVR模型的优点建立组合模型ARIMA-SVR，假设时间序列Yt可视为线性自相关部分Lt与非线性残差Nt两部分的组合，利用ARIMA模型对SPI值进行预测，将结果与实际值相减得到残差，将残差记为非线性部分，带入SVR模型进行预测，最后把两者预测结果相加得到组合结果，即:

1.5 评价验证指标

在回归模型当中，平均绝对误差(Mean Absolute Error，MAE)、均方误差(Mean Square Error，MSE)、RMSE和MAPE是常见的回归预测评估指标，其中MAE和MSE是最基础的评估方法，RMSE和MAPE是回归任务最常用的性能度量，是前两种指标的扩展，不但在多场景下可以使用，而且相对前两种更加准确，因此本文采用RMSE和MAEP作为模型评价的指标。

RMSE均方根误差

MAPE平均绝对百分误差

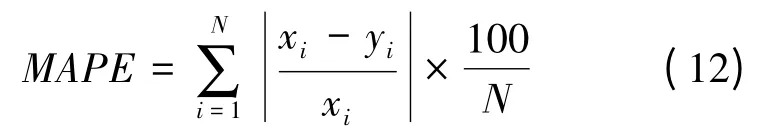
式中，xi是观测值，yi是预测值，N是样本数。RMSE和MAPE越接近0，表示预测值与观测值越接近。

2 实例应用

2.1 数据资料及SPI计算

本文选用1951—2017年河南省国家级气象站郑州站逐日降水量数据来进行计算，原始数据来源于国家气象信息中心提供的中国地面气候资料日值数据集。运用Matlab数学建模软件编写SPI计算程序，分别计算了 1951—2017年的 1、3、6、12个月共4 个尺度的SPI值，记为 SPI1，SPI3，SPI6，SPI12，并通过国家标准气象干旱等级(GB/T20481-2006)规定的干旱分级标准(表1)来表征干旱情况［29］。

2.2 时间序列生成及建模流程

本文使用Python 3.6平台对ARIMA进行建模，并利用Python中matplotlib可视化库对多尺度SPI计算结果进行可视化展示，如图1所示。

2.2.1 平稳化处理及ARIMA模型定阶 由于ARIMA是经过d次差分的平稳时间序列ARMA模型，且通常针对平稳时间序列进行建模，因此在建模前首先应对时间序列的平稳性进行判断，本文采用观察时间序列的时序图和单位根检验(Augmented Dickey-Fuller Test，ADF)来判断平稳性。由图1可得，SPI1、SPI3、SPI6序列无明显的上升和下降趋势，SPI12序列略有上升趋势，进一步对SPI1、SPI3、SPI6和 SPI12进行 ADF检验，在 ADF检验中，原假设为非平稳时间序列且存在单位根，给定显著水平α=0.05，如果检验统计量对应的概率值P＜0.05，则拒绝原假设。其中SPI1、SPI3、SPI6 的ADF检验P值均小于0.05，SPI12的P值为0.36753且显著大于0.05，检验结果见表2，因此判断SPI12序列为非平稳时间序列(非平稳时间序列一定不是白噪声序列)，SPI1、SPI3、SPI6为平稳时间序列。利用差分法对SPI12非平稳时间序列进行平稳化处理，经一阶差分后时间序列趋于平稳(图2)，再对一阶差分后的时间序列进行单位根检验(结果见表3)。表3中P值为0.00128，小于0.05，因此差分之后为平稳时间序列。采用纯随机性检验(Ljung-Box Test)进行白噪声检验，得P值为0.006025，远小于0.05，因此经一阶差分后该序列为平稳非白噪声序列。然后用自相关函数(Autocorrelation Function，ACF)及偏自相关函数(Partial Autocorrelation Function，PACF)来为 ARMA模型定阶(图3)。这里采用观察法为模型ARIMA(p，d，q)定阶，由于图3中ACF在二阶之后均落在置信区间上，所以直接定q=2或1或0;而PACF图置信区间较小，看到在二阶后落在置信区间上，但最后几阶则在置信区间外，因此需要通过时间序列相关性来判断，判断结果如图4所示。由图4可见，曲线在横轴0处相关性最强，最接近0.5，在2处小于-0.25，即p可取的值有0和2。由于d取1，且q可取3个值，p可取2个值，所以ARIMA(p，d，q)模型有6个可取值。

表1 标准化降水指数干旱分级Table 1 Drought classification based on SPI

图1 1951—2017年郑州站多时间尺度SPI变化趋势Fig.1 Trend charts of multi-time scale SPI of Zhengzhou Station from 1951 to 2017

表2 原始序列SPI12单位根检验Table 2 Unit root test of original sequence SPI12

图2 一阶差分(SPI12)Fig.2 First-order difference of SPI12

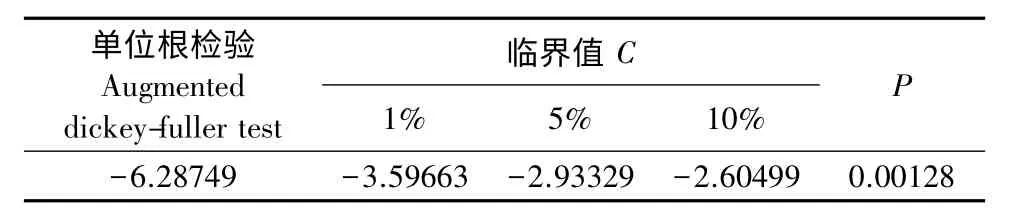
表3 一阶差分后的SPI12单位根检验Table 3 Unit root test after first order difference of SPI12

2.2.2 ARIMA模型参数估计及适用性检验 对ARIMA(p，d，q)的6个可取值分别进行计算，将相关检验结果汇总(表4)。本文采用AIC、BIC准则和标准误差来选取最优模型，由表4可得，ARIMA(2，1，0)的AIC、BIC和标准误差值最小，因此判定为最优模型，即一阶差分后的AR(2)模型为最优模型。对 ARIMA(2，1，0)进行参数估计(结果见表 5)，可得ARIMA(2，1，0)模型的具体形式:

图3 ACF和PACF(SPI12)Fig.3 Autocorrelation function and partial autocorrelation function of SPI12

图4 PACF折线图(SPI12)Fig.4 Line chart of PACF(SPI12)

对一阶差分后的序列拟合AR(2)模型进行残差检验，以评价所建模型的稳定程度，在这里选择QQ残差图及正态分布图来检验模型残差是否是平均值为0且方差为常数的正态分布，QQ残差图中散点均落在拟合直线附近(见图5)，且正态图残差曲线也满足正态分布(见图6)，再通过Ljung-Box检验，得到p值为0.88566，远大于0.1，综合图5和图6，明显符合白噪声序列特征，说明该模型适用于拟合与预测SPI12的变化趋势。选取1951—1995年数据作为训练集，1996—2017年数据作为测试集，应用 ARIMA(2，1，0)来对 SPI12进行 22 a预测(1996-2017)，对于SPI1、SPI3、SPI6 的ARIMA 建模流程同 SPI12，选定模型分别为:SPI1(0，0，2)、SPI3(2，0，0)和 SPI6(1，0，0)，预测结果见图 7。

表4 模型参数检验结果Table 4 The test results of the model parameters

表 5 ARIMA(2，1，0)模型参数Table 5 Parameters of ARIMA(2，1，0)

图5 QQ残差图Fig.5 Residual chart of QQ model

图6 残差正态分布Fig.6 Normal distribution map of residual

2.2.3 SVR模型残差定阶及参数寻优 SVR模型对ARIMA模型残差预测之前，首先要知道过去几个时期的残差会对下一个时期的残差产生的影响，即SVR模型残差定阶。从起始时间开始每次取k个按时间顺序排列的残差数据，并依次排列下来，将排列好的矩阵作为SVR模型的输入，k+1个数据作为模型的输出并保留误差。利用交叉验证的方法，随机取80%的数据作为模型的训练集，其余作为测试集，利用SVR模型训练后对测试集的结果进行预测。在选定阶数为k的情况下，若RMSE第k阶小于第k+1阶的时候，停止循环并输出k;反之，则继续增加阶数。对于SVR模型中的惩罚参数C和径向基函数(Radial basis function，RBF)中的参数γ采用网格寻优(Grid Search，GS)算法进行率定，并完成SVR模型的建模。以1951—1995年作为训练集，1996—2017年作为测试集，利用SVR模型对ARIMA模型所预测的SPI12值的残差进行预测，结果见图7。

2.2.4 组合模型的预测与检验 在ARIMA模型的基础上加入SVR模型进行组合预测时通常有两种方式，一种是并联型，一种是串联型，并联型是通过对两种模型预测结果分别加上权重后重组得到;串联型则是用ARIMA模型进行预测后所得到的残差值输入SVR模型再进行预测，将SVR输出的残差修正值和ARIMA预测值组合得到最终组合模型。两种模型在线性和非线性预测中各有优势，并且ARIMA模型随着时间增加，预测结果越趋于平稳，在用并列组合方式给ARIMA模型权重赋值时无法随着时间长度的增加而改变。因此本文采用串联型进行组合预测，选取1951—1995年4个时间尺度SPI值作为训练集，1996—2017年作为测试集，将ARIMA模型与ARIMA+SVR组合模型预测结果与实际4个时间尺度SPI值进行比对，结果见图8。

图7 SVR模型残差预测(SPI12)Fig.7 Residual prediction of SVR model(SPI12)

图8 ARIMA模型与ARIMA-SVR组合模型的多时间尺度SPI值的预测(1996-2017)Fig.8 Prediction of multi time-scale SPI based on ARIMA and ARIMA-SVR models

表6 ARIMA模型与ARIMA-SVR组合模型的均方根误差和平均绝对百分误差Table 6 RMSE and MAPE values for ARIMA and ARIMA-SVR model

利用RMSE和MAPE两种评价指标对4个时间尺度的两种模型预测结果进行评价，结果见表6。从表中数据可以发现两种模型在SPI1时间尺度的预测效果最差，ARIMA模型在SPI12尺度预测效果最好，在 SPI3和 SPI6时间尺度预测效果仅次于SPI12。组合模型在各时间尺度预测效果都比单独ARIMA模型预测效果好，在SPI12预测效果最好，随着时间尺度减小，预测精度降低。

3 讨论与结论

本文引入了反映干旱强度和持续时间的SPI指数，以郑州市气象站点为例，利用ARIMA模型和ARIMA-SVR组合模型对不同时间尺度的SPI序列进行建模预测，并利用RMSE和MAPE两种回归模型预测指标进行评价，得到如下结论:

1)从ARIMA模型的预测结果来看，该模型对较长时间尺度的预测精度较高，对较短时间尺度的预测精度较低，随着时间尺度增加，拟合精度提高。对于SPI12预测效果最好，对SPI1预测效果最差，主要由以下原因导致:ARIMA模型本质上是一种整体线性自回归模型，该模型预测趋势会随着测试集时间增长而逐渐趋于平稳。因为SPI1相对于其他3个时间尺度数据量最多，整体趋于严平稳(严平稳表示的分布不随时间的改变而改变)，所以预测精度最低，同理，SPI3、SPI6和SPI12时间尺度逐渐增加，数据量逐渐减少，越来越趋于弱平稳(期望与相关系数不变，未来时刻值依赖于过去时刻的值)，因此拟合精度整体逐渐提高。

2)从组合模型的预测结果来看，对多尺度SPI值利用ARIMA模型预测线性部分，用SVR模型预测非线性部分，叠加在一起的组合模型在各个时间尺度的预测精度均比单一ARIMA模型的预测精度高。从多时间尺度来看，该模型预测精度随着时间尺度的增加而提高，对SPI12预测效果最佳，主要是由于ARIMA模型对SPI12预测精度最高，残差最小，所以传入SVR模型中的误差就小，最后组合预测结果也更加准确。同理，随着时间尺度的减小，SPI6、SPI3和SPI1的ARIMA模型预测精度也降低，则组合模型的预测精度也随之降低。