有限长冲击响应滤波器线性相位条件证明

陈国泰,李金赐,廖延初,张赛男,郭春凤

（福建技术师范学院 a.无损检测技术福建省高校重点实验室；b.电子与信息工程学院,福建福清 350300 ）

非线性相位会导致各个频率的波形到达的时间不同,使信号所表现的效果被破坏.在立体语音、通信以及图像处理等场合要求滤波器具有线性相位特性,以保证信号没有相位失真或没有明显的相位失真.有限长冲击响应（Finite Impulse Response, FIR）数字滤波器在冲击响应序列对称的条件下具有线性相位特性,因此FIR滤波器得到广泛的应用.

现有文献[1-4]指出FIR数字滤波器冲击响应序列的对称性与线性相位特性之间形成充分必要条件关系.文献[1-4]中虽然有涉及线性相位必要条件方面的证明,但是没有给出严格和完整的证明过程.汪芙平等从连续傅里叶变换的角度,给线性相位必要条件提供了较为严格清晰的证明过程[5].

本文在冲击响应序列傅里叶变换的基础上开始线性相位必要条件的证明,证明过程与序列紧密结合,因此对序列对称性的理解更为直观.本文也将线性相位充分条件的证明做了阐述,使线性相位充分必要条件的证明更为完整.

1 命题描述

FIR数字滤波器冲击响应序列与线性相位之间的关系描述如下：

命题1：若N阶FIR数字滤波器的单位脉冲响应h(n)(n=0,…,N-1)为实序列,则该滤波器具有线性相位的充分必要条件是h(n)为对称序列.

2 线性相位的充分条件证明[4]

命题1的充分性很容易证明,很多教材提供了推导过程.这里为了命题1证明的完整性,对充分性也进行证明.

首先,假设h(n)是偶对称,即h(n)=h(N-1-n),则序列h(n)的傅里叶变换函数为

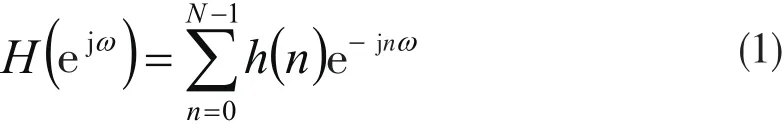
它是以2π为周期的关于ω的函数.

当N为偶数时,对式(1)可按对描述为

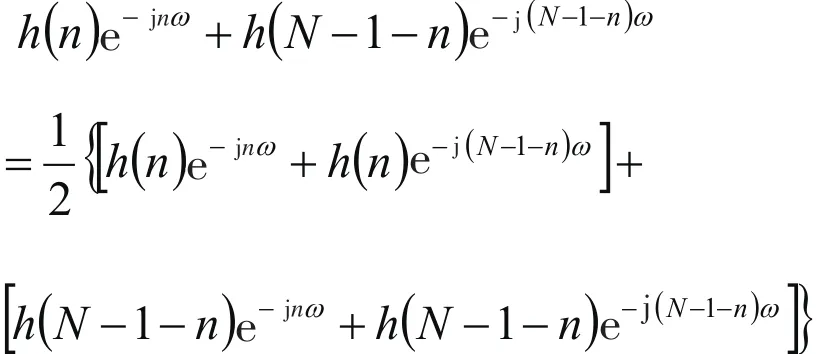
当N为奇数时,式(3)仍成立.

通过分析N为奇数或偶数下,式(4)和式(7)在为0、π和2π下的函数值和对称性,可以得到式(4)和式(7)在什么时候适合设计哪种FIR数字滤波器,如表1所示.

3 线性相位的必要性证明

当一个FIR数字滤波器具有线性相位,则可将式(1)表示为

表1 不同对称性和长度下所适合设计的FIR数字滤波器

整理可得

又因为为实函数,故其虚部部分为0,即有[6]

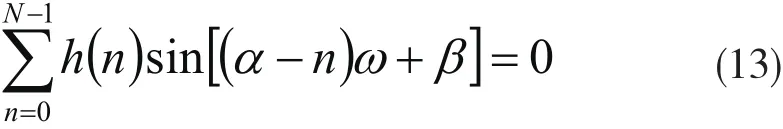
下面观察sin [(α-n)ω+β]在不同n下ω从0到2积分的正交性.

设 n1和 n2,则

前面分析显示,当2α≠(N -1)时,序列h(n)中开头一部分或最后一部分是全零元素,这时序列h(n)的有些长度实际上只有2 N -1-2α或2α+1,因为,为了真正考虑N阶FIR数字滤波器,那么2α必须为N-1.综合上述分析,可得如表2的结果.

表2 不同长度和β下FIR数字滤波器序列的对称性

4 结论

相比文献[5],本文的证明篇幅略冗长一些,但是本文的证明主要是基于序列上,在文献[5],该文作者将序列构成一个由冲击脉冲函数叠加的连续函数并在连续时间傅里叶变换上对线性相位的必要性进行证明.本文提供另一种证明参考,文献[6]也对该问题做了简要说明,而本文提供了详细的证明过程,并将充分必要条件的证明整合在一起,使证明更具完整性.