弯曲应力下钢筋混凝土碳化性能数值模拟分析

冯晓爽，任 军，刘 燕，赵胜利

（1.河北农业大学 城乡建设学院，河北 保定 071001；2.河北建设集团股份有限公司，河北 保定 071001）

随着自然环境的恶化，混凝土结构的耐久性问题越来越受到国内外学者的关注。其中，碳化损伤可以导致结构的钢筋发生锈蚀，造成结构承载力的下降。研究混凝土碳化性能的常规方法是在标准试验条件下对混凝土进行快速碳化试验，但这种方法易受到试验空间、时间、器材、材料等限制，而利用有限元分析软件对混凝土碳化进行数值模拟分析可以突破这种局限。目前，利用ANSYS 软件对混凝土进行碳化模拟分析所取得的成果颇多［1-7］。但是，这些成果研究对象均为素混凝土，应力也仅考虑了轴压轴拉应力，没有考虑掺合料和其他应力形式的影响。所以，目前的研究成果和实际工程仍然具有不符之处，还不具备广泛的应用性。

本文以弯曲应力下钢筋混凝土构件为研究对象，采用不同的混凝土配合比进行快速碳化试验，寻找出弯曲应力水平和粉煤灰掺量对混凝土的碳化速度影响系数。并以此为基础，利用ANSYS 有限元分析软件对本试验中的钢筋混凝土构件进行碳化模拟，充分考虑了弯曲应力、粉煤灰掺量在数值模拟中对碳化深度的影响，为实际工程中碳化损伤研究提供科学合理的依据。

1 钢筋混凝土快速碳化试验

1.1 试验方案

混凝土试块强度为C30，配合比如表1：

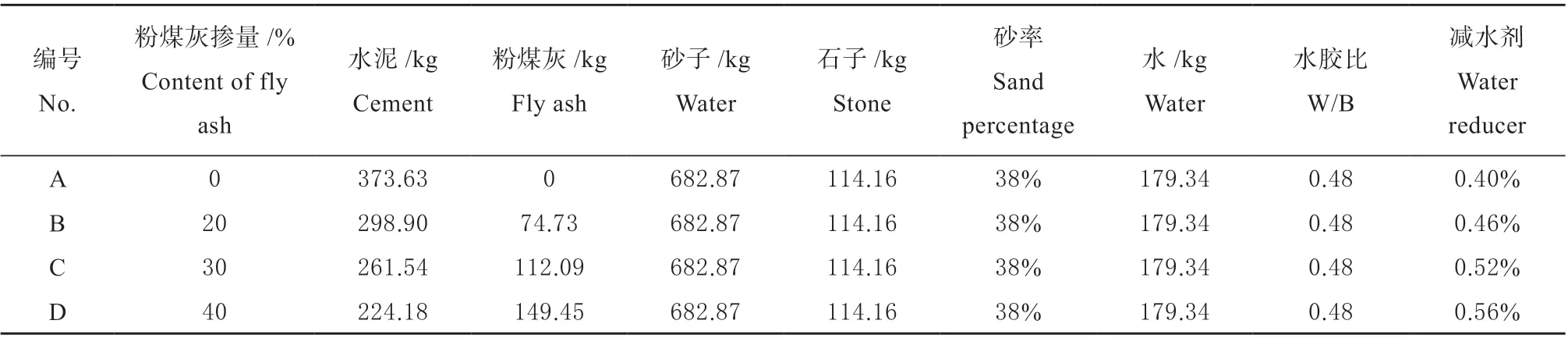
表1 混凝土配合比Table 1 The proportions ratios of concrete

试件采用100 mm×100 mm×300 mm 的长方体构件，利用扭矩扳手来施加不同比例的应力，图1为试块尺寸及弯曲持载装置和配筋图：

图1 加载装置及试件配筋图(单位：mm)Fig. 1 Bending stress loading device and concrete reinforcement diagram (Unit:mm)

根据（GB/T50082—2009）《普通混凝土长期性能和耐久性试验方法标准》中相关要求进行试验，对构件施加相应弯曲应力后，进行持荷下的快速碳化试验。当快速碳化至7、14、28 d 时将构件取出，沿裂缝测量其跨中部位碳化深度。

1.2 试验结果分析

不同配合比下的钢筋混凝土构件在不同大小的弯曲应力水平、不同碳化龄期下的碳化深度数据如表2 所示：

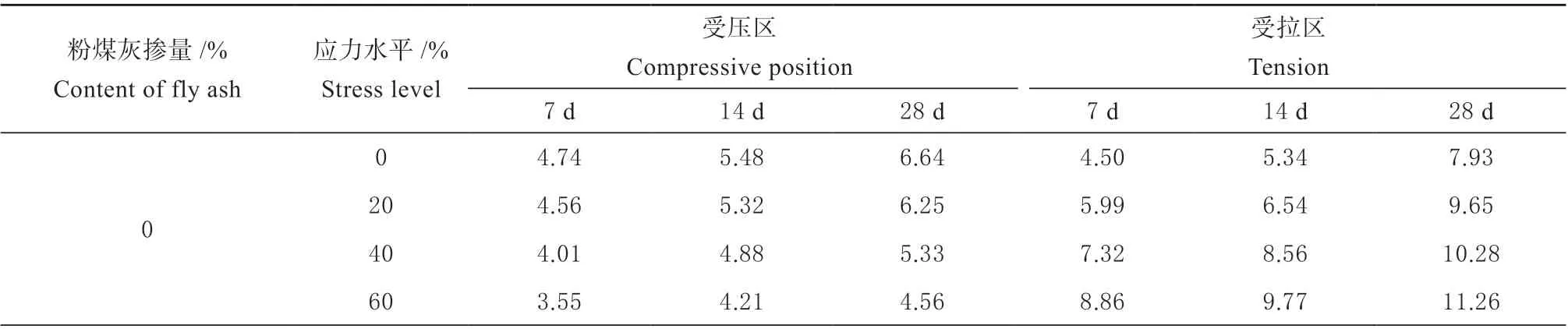
表2 不同弯曲应力下混凝土试块碳化深度Table 2 Carbonation depth of concrete members under different bending stress mm

续表：

1.2.1 粉煤灰掺量影响 由表1 可知，当应力、碳化龄期一定时，钢筋混凝土构件碳化深度均随着粉煤灰掺量的提高而增加。加入粉煤灰后，粉煤灰与水泥水化产物反应生成的胶凝物质会使构件更加致密，影响CO2的扩散从而抑制构件碳化深度，但另一方面粉煤灰火山灰反应会降低混凝土碱性，加剧碳化反应速率。由试验结果可知，粉煤灰加剧作用要大于抑制作用，从而加剧混凝土碳化损伤。

1.2.2 弯曲应力影响 由试验结果可知，弯曲拉应力促进了构件碳化损伤，弯曲压应力抑制了构件碳化损伤。这是由于弯拉应力会加剧构件裂缝发展，提高CO2侵入速度，而弯压应力会使裂缝趋于闭合，从而阻碍CO2向构件内部扩散。但当弯压应力过大时，又会压碎受压区混凝土使其裂缝贯通，从而促进构件碳化，故本文对弯压应力研究时应力范围保持在60%极限应力内。

2 粉煤灰掺量与弯曲应力影响系数研究

根据试验数据，计算不同弯曲应力水平及粉煤灰掺量对应的碳化速度系数α，以粉煤灰掺量为0%、弯曲应力水平为0 的钢筋混凝土构件为基准组，分别调整影响变量来分析粉煤灰掺量及弯曲应力水平影响系数k（k 为α 与基准混凝土碳化速度系数比值）。采用如下碳化速度系数计算公式［8-9］：

式中：D：钢筋混凝土试块碳化深度，mm；

n：试验测定次数；

t：碳化时间，d。

2.1 弯拉应力影响系数

按式（1）计算得到的混凝土在不同弯拉应力下的碳化速度系数α1和弯拉应力影响系数k1，见表3：

表3 不同弯拉应力下的α1 和k1 取值Table 3 Values of α1 and k1

对k1和弯拉应力水平St进行拟合，可得弯拉应力影响系数方程：

2.2 弯压应力影响系数

按式（1）计算得到的不同弯压应力下的碳化速度系数α2和弯拉应力影响系数k2，见表4：

表4 不同弯压应力下的α2 和k2 取值Table 4 Values of α2 and k2

对k2和弯压应力水平Sc进行拟合，可得弯压应力影响系数：

2.3 粉煤灰掺量影响系数

根据式（1）可得4 种粉煤灰掺量的碳化速度影响系数α3和粉煤灰掺量影响系数k3，见表5：

表5 不同粉煤灰掺量下的α3 和k3 取值Table 5 Values of α3 and k3

对k3和粉煤灰掺量FA 进行拟合，可得粉煤灰掺量影响系数：

3 弯曲应力下钢筋混凝土碳化过程的数值模拟

混凝土碳化主要分为两部分，即CO2在混凝土内部的扩散和与其内部碱性物质反应两部分。混凝土碳化反应过程与热传导十分相似，所以将ANSYS 瞬态热分析方法类比应用到碳化模拟中：将CO2扩散控制方程∂C/∂t=D▽C-r 代替传导方程∂T/∂t=a2▽T+f（x, y, z, t），CO2浓度C 代替热传导温度T，CO2扩散系数Dc代替将热传导系数k，CO2碳化反应速率r 代替传导吸热率f（x, y, z, t）。由此可知，在碳化模拟过程中，确定CO2扩散系数Dc和CO2碳化反应速率r 的数值十分关键。

3.1 碳化模型的建立

有限元的模型为100 mm×100 mm 的正方形混凝土截面，因钢筋并不传递CO2，所以在模型中将钢筋部位去除，不设定参量。如图2 所示将有限元模型划分为100×100 的网格：

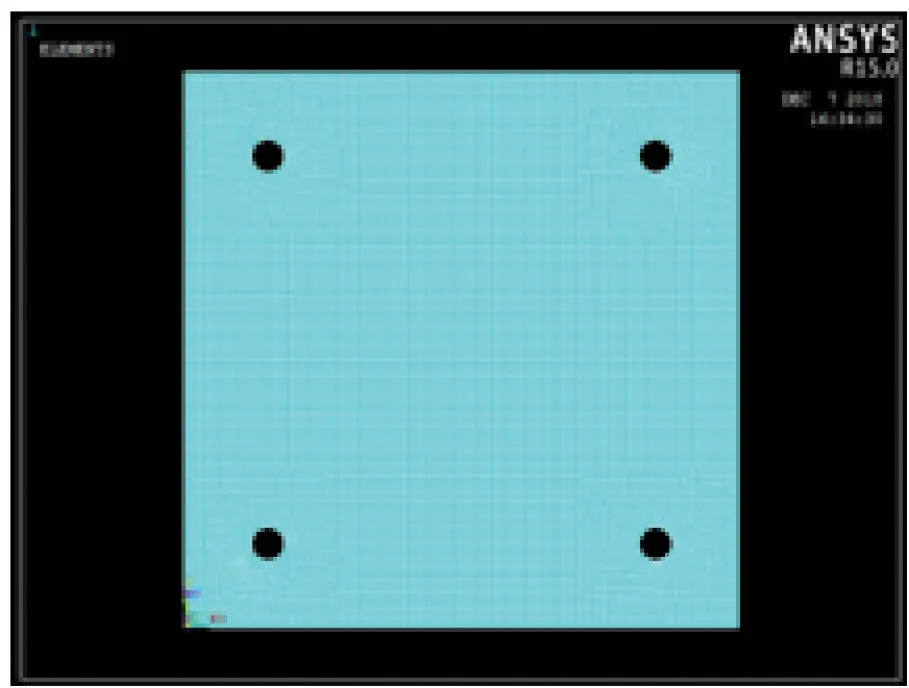
图2 碳化模型网格划分Fig. 2 Carbonization model meshing

3.2 参数输入

通过已有的研究结果［1-7］，对Dc赋值规律及取值结果如下：

式中：Dc,0：混凝土碳化前CO2扩散系数；

查阅文献［1-7］发现，对于CO2扩散系数Dc，鲜有文献将弯曲应力水平和粉煤灰掺量考虑进Dc方程中，这大大限制了混凝土碳化数值模拟应用范围，故本文对此进行如下改进：

应力影响了混凝土裂缝发展，从而影响了CO2扩散系数Dc。现阶段，袁承斌［10］研究所得的轴拉、轴压应力对混凝土碳化反应影响系数被诸多学者用于应力对混凝土CO2扩散系数的影响函数F(σ)中。所以，本文参考袁承斌研究方法，将第二节研究所得弯曲应力影响系数应用到Dc中，即式（5）中的F4(σ)，从而进行弯曲应力下混凝土的碳化数值模拟分析。

粉煤灰掺量对混凝土CO2扩散系数影响公式F（FA）可根据文献［11］中的试验数据得到：

式中：FA：粉煤灰掺量。

参照上述文献，本文将式（6）应用在混凝土CO2扩散系数Dc方程中，即式（5）中的F5(FA)，充分考虑了粉煤灰掺量对混凝土碳化数值模拟的影响。

对r 赋值规律及取值结果如下：

式中：r0：混凝土理想状态下碳化反应速率。

文献［1-7］对于碳化反应速率r 的方程也没有考虑粉煤灰掺量的影响，而通过试验发现，粉煤灰可以改变混凝土内部碱性物质浓度大小，对碳化反应速率产生影响。

粉煤灰的存在一方面降低了混凝土内部碱性物质的浓度，使二氧化碳与混凝土内部碱性物质反应的速度加快，对碳化反应速率r 产生影响；同时粉煤灰在一定程度上使混凝土的致密性发生变化，对CO2在混凝土内部的扩散产生影响，即对CO2扩散系数Dc产生影响。通过前文试验数据发现，粉煤灰的加入最终提高了混凝土构件的碳化深度，即粉煤灰掺量对r 的影响作用要大于对Dc的影响作用。现阶段对粉煤灰掺量对混凝土碳化反应速率r 的研究颇少，式（4）恰好反应的是粉煤灰掺量对r 的影响，将式（4）代入到计算碳化反应速率r 方程中比较合理，误差也较小。

3.3 模拟结果

通过模拟，可得到不同损伤下的钢筋混凝土构件碳化云图。根据云图可以分析数值模拟中粉煤灰掺量、碳化龄期和弯曲应力水平对混凝土的影响规律。

需要解释的是，实际受弯构件的受压面或受拉面是2 个相对的面，只存在于构件横截面这一个面上。但本文是分别对弯压应力和弯拉应力进行模拟，比如在对构件进行弯拉应力模拟时，模型的4 个面代表的都是受拉面的碳化情况，即它们所代表的均是实际混凝土的受拉面。

3.3.1 粉煤灰掺量的影响 取碳化龄期为28 d，弯拉应力水平为40%时，4 种粉煤灰掺量的混凝土中CO2扩散云图，用于分析粉煤灰掺量对其的影响。不同粉煤灰掺量混凝土的CO2扩散云图如图3所示：

图3 不同粉煤灰掺量下混凝土中CO2 扩散云图Fig. 3 CO2 diffusion pictures in concrete at different fly ash contents

分析可知，SMN 表示混凝土内部中心CO2的浓度值，也就是CO2扩散最前端的数字，其值越大，表示侵入到混凝土内部的CO2浓度值就越高。由图3 所示CO2扩散云图可得，SMN-0%粉煤灰掺量=0.632E-5，SMN-20%粉煤灰掺量=0.666E-5，SMN-30%粉煤灰掺量=0.731E-5，SMN-40%粉煤灰掺量=0.835E-5。由小到大分别是SMN-0%粉煤灰掺量＜SMN-20%粉煤灰掺量＜SMN-30%粉煤灰掺量＜SMN-40%粉煤灰掺量，可以反映出混凝土内部CO2浓度随着粉煤灰掺量的增加而逐渐增加，说明随着粉煤灰掺量的增加混凝土的碳化损伤加剧，与试验得出的结论一致，同时也验证了在混凝土碳化模拟方程中补充的关于粉煤灰掺量对其参数的影响系数的合理性。

3.3.2 碳化龄期影响 取粉煤灰掺量为0%、弯拉应力为0 时，不同碳化龄期的碳化云图用于分析碳化龄期对其的影响。图4 表示在不同碳化龄期时CO2在混凝土中的扩散云图：

图4 不同碳化龄期下CO2 在混凝土中的扩散云图Fig. 4 CO2 diffusion on pictures in concrete at different ages of carbonization

图4 可得，SMN-碳化7 d=0.271E-7，SMN-碳化14 d=0.403E-6,，SMN-碳化28 d=0.354E-5。从小到大分别是：SMN-碳化7 d ＜SMN-碳化14 d＜SMN-碳化28 d，说明混凝土内部的CO2浓度随着碳化龄期的增加也在不断的增加，与试验中所得的变化规律一致。

3.3.3 弯拉应力水平的影响 选取碳化龄期28 d，粉煤灰掺量为30%时，4 种弯拉应力水平下混凝土中CO2扩散云图用于分析弯拉应力对其影响。不同弯拉应力水平的CO2在混凝土中的扩散云图如图5 所示：

图5 不同弯拉应力下混凝土中CO2 扩散云图Fig.5 CO2 diffusion picturesof concrete under different bending-tension stress

由图5 所示的云图可知，SMN-0%极限弯拉应力=0.407E-5，SMN-20% 极限弯拉应力=0.580E-5，SMN-40% 极 限 弯 拉 应 力=0.731E-5，SMN-60% 极限弯拉应力=0.860E-5。从小到大分别为SMN-0%极限弯拉应力＜SMN-20%极限弯拉应力＜SMN-40%极限弯拉应力＜SMN-60%极限弯拉应力，说明当碳化龄期和粉煤灰掺量一定时，混凝土内部CO2的浓度值随弯拉应力水平的增加而逐渐增加，弯拉应力在一定程度上对混凝土的碳化起到了不利影响。符合试验中所得的弯拉应力作用下混凝土的碳化规律，其主要原因在于增加弯拉应力会使混凝土内部的裂缝变宽，CO2更容易扩散到混凝土内部，使混凝土内部的CO2浓度升高，造成混凝土的碳化损伤越来越严重。

3.3.4 弯压应力大小的影响：

同样取碳化龄期为28 d、粉煤灰掺量为30%时，不同弯压应力水平的混凝土CO2扩散云图分析弯压应力对其影响。不同弯压应力水平的混凝土中CO2扩散云图如图6 所示：

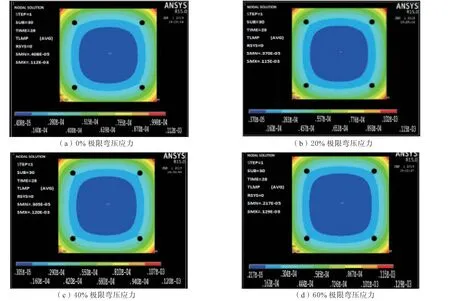
图6 不同弯压应力水平下CO2 在混凝土中的扩散云图Fig. 6 Diffusion pictures of CO2 in concrete under four kinds of bending-press stress levels

由图6 可得，SMN-0%极限弯压应力=0.408E-5，SMN-20%极限弯压应力=0.370E-5，SMN-40%极限弯压应力=0.305E-5，SMN-60%极限弯压应力=0.217E-5。则SMN-0%极限弯压应力＞SMN-20%极限弯压应力＞SMN-40%极限弯压应力＞SMN-60%极限弯压应力，表明当碳化龄期和粉煤灰掺量一定时，混凝土的碳化深度随着弯压应力水平的增加逐渐减小，与弯拉应力不同，弯压应力阻滞了混凝土的碳化。符合试验中所得的弯压应力水平下的混凝土碳化规律，这种规律的主要原因均是因为弯压应力使混凝土内部裂缝宽度变小，抑制了混凝土中CO2的扩散，降低了CO2浓度，在一定程度上抑制了混凝土的碳化损伤。但同样需要说明的是，本试验中弯压应力水平仅取到了0.6，当弯压应力再持续增大时，产生的过大的压应力会破坏混凝土内的裂缝，从而压碎混凝土，又会加大CO2的扩散，从而表现出不同的碳化性能。

4 模拟数据分析

本文取碳化龄期为28 d 的混凝土进行研究碳化锋面CO2浓度分布规律。根据试验中在不同损伤条件下测得的碳化深度，在其所对应的模拟结果中，找出与其数值相对应的碳化锋面位置的CO2浓度，具体数值如表6 所示：

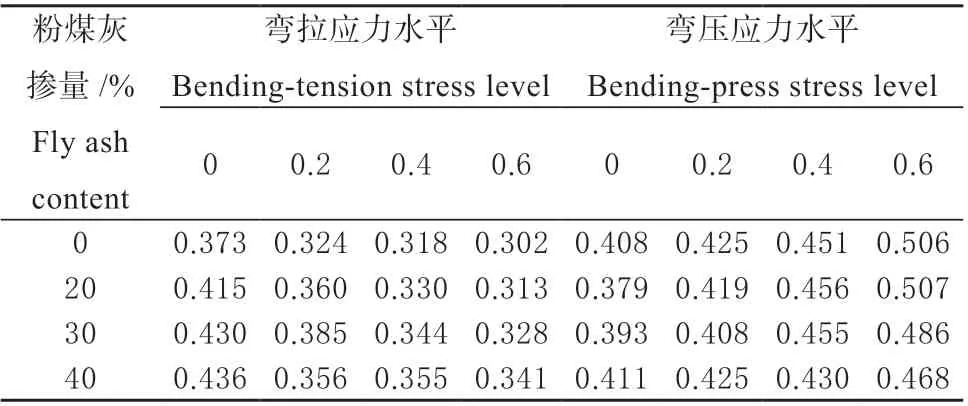
表6 CO2 同粉煤灰掺量和弯曲应力水平下碳化锋面的CO2 浓度Table 6 CO2 concentration of carbonized front under different fly ash contents and bending load stress 10-4kg/m3

笔者推测，碳化深度与粉煤灰掺量、弯拉应力水平的大小、碳化锋面CO2浓度之间存在着某种函数关系，即：

X=F（C, St, FA）

经多次尝试，回归分析拟合为如下函数关系：

X=105·C·（-2.79S2t+4.69St+0.79FA+1.93）（8）

式中，X：混凝土碳化深度；

C：碳化锋面的CO2浓度；

St：弯拉应力水平。

表7 为该回归分析中的主要回归统计和方差分析指标：

表7 方差分析指标和回归统计Table 7 Variance analysis indicators and regression statistics

由表7 可知，该回归方程的Significance F 为8.3E-07，远远小于0.05 的显著性水平；相关系数Multiple R 反映的是回归方程中自变量和因变量之间的相关性，该回归方程的相关系数为0.96，说明该回归方程的自变量和因变量之间的相关程度高；调整后的复测定系数Adjusted R2为90%，表示自变量可以解释因变量变差的90%，综合3 个指标来看，该回归方程的回归效果显著。说明式（8）中的各变量之间的相关程度高。

同样，粉煤灰掺量、弯压应力水平的大小、碳化锋面CO2浓度和其所对应的碳化深度之间也会存在类似于式（8）的函数关系，即：

X=G（C, Sc, FA）

经多次尝试，回归分析拟合为如下函数关系：

X=105·C·（-2.24S2c+1.43Sc+2.53FA+1.75）（9）

式中，X：混凝土碳化深度；

C：碳化锋面的CO2浓度；

Sc：弯压应力水平。

表8 为该回归分析中的方差分析指标及主要回归统计：

表8 方差分析指标及回归统计Table 8 Variance analysis indicators and regression statistics

通过对式（8）中碳化深度、粉煤灰掺量、弯拉应力水平和碳化锋面CO2浓度的回归分析可知，式（9）中碳化深度、粉煤灰掺量、弯压应力水平和碳化锋面CO2浓度之间同样具有较高的相关性。基于此，可以较为科学地用上述公式表达出碳化深度、粉煤灰掺量、弯曲应力水平和碳化锋面CO2浓度之间的关系，这对于之后研究在弯曲应力水平下的钢筋混凝土碳化模拟具有一定的参考性。

5 结论

（1）试验显示：粉煤灰掺量的增加提高了混凝土碳化深度；弯拉应力会促进混凝土的碳化损伤；而一定范围内的弯压应力则会抑制混凝土的碳化损伤；

（2）建立粉煤灰掺量、弯曲应力水平对钢筋混凝土碳化速度的影响公式，为混凝土碳化模型提供参考；

（3）数值模拟结果中，粉煤灰掺量和弯曲应力水平对钢筋混凝土碳化的影响规律均与试验所得结果一致，证明了该方法的可行性，为弯曲应力下粉煤灰混凝土碳化的数值模拟提供了新思路。

（4）通过试验模拟相结合的方法，推导出碳化深度与粉煤灰掺量、弯曲应力水平、碳化锋面CO2浓度之间的回归关系，为混凝土碳化模拟提供参考。