Representing surface wind stress response to mesoscale SST perturbations in western coast of South America using Tikhonov regularization method*

CUI Chaoran , ZHANG Rong-Hua , , WANG Hongna WEI Yanzhou

1 Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China

2 Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China

3 University of Chinese Academy of Sciences, Beijing 100049, China

4 Qingdao National Laboratory for Marine Science and Technology, Qingdao 266000, China

5 State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012, China

Received Feb. 20, 2019; accepted in principle May 28, 2019; accepted for publication Sep. 5, 2019 © Chinese Society for Oceanology and Limnology, Science Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract Interaction between mesoscale perturbations of sea surface temperature (SST meso) and wind stress (WS meso) has great infl uences on the ocean upwelling system and turbulent mixing in the atmospheric boundary layer. Using daily Quik-SCAT wind speed data and AMSR-E SST data, SST meso and WS meso fi elds in the western coast of South America are extracted by using a locally weighted regression method (LOESS). The spatial patterns of SST meso and WS meso indicate strong mesoscale SST-wind stress coupling in the region. The coupling coeき cient between SST meso and WS meso is about 0.009 5 N/(m 2 ∙°C) in winter and 0.008 2 N/(m 2 ∙°C) in summer. Based on mesoscale coupling relationships, the mesoscale perturbations of wind stress divergence (Div(WS meso)) and curl (Curl (WS meso)) can be obtained from the SST gradient perturbations, which can be further used to derive wind stress vector perturbations using the Tikhonov regularization method. The computational examples are presented in the western coast of South America and the patterns of the reconstructed WS meso are highly consistent with SST meso, but the amplitude can be underestimated signifi cantly. By matching the spatially averaged maximum standard deviations of reconstructed WS meso magnitude and observations, a reasonable magnitude of WS meso can be obtained when a rescaling factor of 2.2 is used. As current ocean models forced by prescribed wind cannot adequately capture the mesoscale wind stress response, the empirical wind stress perturbation model developed in this study can be used to take into account the feedback efference ects of the mesoscale wind stress-SST coupling in ocean modeling. Further applications are discussed for taking into account the feedback efference ects of the mesoscale coupling in largescale climate models and the uncoupled ocean models.

Keyword: mesoscale air-sea coupling; Tikhonov’s regularization method; western coast of South America * Supported by the National Key Research and Development Program of China (No. 2017YFC1404102(2017YFC1404100)), the National Program on Global Change and Air-sea Interaction (No. GASI-IPOVAI-06), the National Natural Science Foundation of China (Nos. 41490644(41490640), 41690122(41690120)), the Chinese Academy of Sciences Strategic Priority Project (No. XDA19060102), the NSFC Shandong Joint Fund for Marine Science Research Centers (No. U1406402), and the Taishan Scholarship and the Recruitment Program of Global Experts ** Corresponding author: rzhang@qdio.ac.cn

1 INTRODUCTION

Wind stress is a main driver of the ocean circulation and plays an important role in the ocean-atmosphere interaction. Many previous studies often concentrated on the large-scale ocean-atmosphere interaction (Zhang and Gao, 2016, 2017), and have found that a high wind stress magnitude leads to cold sea surface temperature (SST) through the enhanced latent heat fl ux (Xie and Philander, 1994), suggesting that there was a negative correlation between the large-scale wind stress and SST. As high-resolution measurements became available, mesoscale air-sea interactions can be studied. It is found that there is signifi cant coupling between the ocean and atmosphere at a mesoscale scale of about 10-100 km, with mesoscale perturbations of wind stress (WSmeso) magnitude being positively correlated with those of sea surface temperature (SSTmeso).

The mesoscale coupling between wind stress and SST has been examined for several decades. For example, Sweet et al. (1981) found that the magnitude of cross-front wind stress was increased when wind was passing from cold to warm waters in the Gulf Stream. More observations in other regions also verifi ed that the wind stress magnitude was enhanced (weakened) when the wind fl owed over the warm (cold) waters (Businger and Shaw, 1984; Giordani et al., 1998). Furthermore, the satellite data confi rmed that there was a positively linear relationship between WSmesomagnitude and SSTmeso(Chelton et al., 2001; Bourras et al., 2004). Based on the spatial derivation of the positive relationship between SSTmesoand WSmesomagnitude, Chelton et al. (2004) demonstrated that mesoscale perturbations of wind stress curl (Curl(WSmeso)) and divergence (Div(WSmeso)) were linearly proportional to the crosswind ( ∇crossSSTmeso) and downwind ( ∇downSSTmeso) components of SST gradient perturbations, respectively. These relations have been verifi ed by observations and model simulations (O’Neill et al., 2005, 2010b, 2012; Chelton et al., 2007; Castelao, 2012; O’Neill, 2012; Frenger et al., 2013).

There are two mechanisms which can explain WSmesoresponse to SSTmeso(Small et al., 2008; Chelton and Xie, 2010; Gao et al., 2018). One is the downward momentum transport in the atmosphere. When wind fl ows from cold to warm water, warm SSTmesocan afference ect turbulent heat fl ux and lead to an intensifi cation of turbulence within the atmospheric boundary layer, and thus there is an increased downward momentum transport. Subsequently, an increased WSmesomagnitude is induced over the warm fl ank of fronts and eddies. The second mechanism is the horizontal pressure adjustment. This mechanism is related to the changes of sea level pressure. According to observations, the negative sea level pressure perturbations are induced over the warm SSTmeso. Then, WSmesoin the upstream (downstream) of warm SSTmesois accelerated (decelerated). Note that the spatial patterns of Div(WSmeso) corresponding to the SSTmesoare difference erent in the two mechanisms. In the case of the downward momentum transport mechanism, a dipole pattern of the Div(WSmeso) is expected (Chelton et al., 2004). This is because when WSmesoincreases over the warm SSTmeso, WSmesodiverge (converge) in the upstream (downstream) of warm SSTmeso. In contrast, a monopole pattern of the Div(WSmeso) is seen in the context of the horizontal pressure adjustment mechanism as WSmesoconverge over the whole warm SSTmeso(Minobe et al., 2008). The difference erences in the spatial patterns of Div(WSmeso) between the two mechanisms have been the standard metric to measure which mechanism is dominant in the mesoscale SST-wind stress coupling.

Previous studies indicated that the mesoscale SSTwind stress coupling had signifi cant efference ect on the atmosphere and ocean dynamics. On one hand, SSTmesocan afference ect the wind and cloud activity in the atmospheric boundary layer. Piazza et al. (2016) showed that the SSTmesohad an upscaling impact on the tropospheric wind and storm tracks in the Gulf Stream region. Renault et al. (2016) showed that the nearshore wind shape could be modulated by SSTmeso. On the other hand, WSmesocan afference ect the SSTmesoin return. Wei et al. (2017) showed that WSmesohad a negative feedback on SSTmesoby the means of surface heat fl ux in the Kuroshio Extension. In addition, the mesoscale SST-wind stress coupling also has great infl uence on the Ekman pumping. For example, Gaube et al. (2015) showed that the eddy-induced spatially variability of SST could afference ect the wind stress curl which was an important factor to drive the wind forced upwelling. Thus, Ekman upwelling could be infl uenced by the mesoscale SST-wind stress coupling in the regions with strong SSTmeso. This conclusion was verifi ed by other studies. Seo et al. (2016) also showed that the Ekman pumping was modifi ed by SSTmesoin the California Sea. The similar results were also found in the Arabian Sea (Seo, 2017). Furthermore, mesoscale eddy activities can also be afference ected by the mesoscale SST-wind stress coupling. Ma et al. (2016) showed that the eddy potential energy dissipation was strongly afference ected by the mesoscale SST-wind stress coupling and the Kuroshio Extension Jet could be weakened by about 20%-40% if the mesoscale SST-wind stress coupling was neglected in the eddy-resolving coupled climate model. Jin et al. (2009) applied an empirical air-sea coupled model that was constructed by the observed SST-wind stress relationship to a geographically idealized coastal upwelling system. They showed that if the mesoscale SST-wind stress coupling was included in the model, wind stress was weakened in the coastal sea area because of the cold coastal SST efference ect. The ofference shore Ekman upwelling was strengthened through the SST-induced wind stress curl. Besides, the eddy kinetic energy was reduced by about 25%.

The previous studies indicated that the coupling coeき cients between WSmesoand SSTmesoderived from high spatial resolution models were weaker than observations (Bryan et al., 2010; Chelton and Xie, 2010). In particular, the correlation between WSmesoand SSTmesofrom low spatial resolution models was opposite to observations (Bryan et al., 2010). The reason why the climate models cannot simulate the mesoscale SST-wind coupling well is that depicting WSmesorequires not only the high resolution but also accurate parameterizations of relevant physical processes in the marine atmospheric boundary layer. Therefore, it is necessary to represent mesoscale wind stress-induced feedback in the regions where mesoscale air-sea interactions are strong.

For example, Zhang and Busalacchi (2009) developed an empirical model to depict wind stress induced by tropical instability waves (TIW)-related SST perturbations in the eastern tropical Pacifi c Ocean. Using the observed data, they applied a combined singular value decomposition (SVD) analysis to the zonal high pass fi ltered TIW-related SST and wind stress fi elds. They found the SVDbased analysis technique could efference ectively extract TIW-induced covariability patterns in the atmosphere and ocean. However, the magnitude of reconstructed TIW-related wind stress fi elds was dependent on the number of SVD modes which were included in the statistical model-based simulation. Wei et al. (2017) studied the efference ects of the mesoscale wind stress-SST coupling on the Kuroshio extension. In their method, WSmesowas obtained directly from SSTmesousing observed coupling coeき cient between WSmesoand SSTmesoand the direction of WSmesowas taken the same as the wind stress climatology. O’Neill et al. (2010a) showed that SSTmesocould modify surface wind direction signifi cantly and the maximum of the changed direction could reach about 4°-8° in the strong boundary current regions. This means the wind direction is also a factor to be considered in approximating the wind stress vector perturbations.

The main goal of our study is to fi nd a useful way to represent WSmesoin response to SSTmesoin the western coast of South America. The western coast of South America is a strong boundary upwelling system and hosts intense eddy and biological activity due to the complicated hydrography structure (Strub et al., 1998; Capet et al., 2008). Satellite observations have proved that there is strong mesoscale SST-wind stress coupling in this area (Oerder et al., 2016). On one hand, because SSTmesocan infl uence wind stress curl that is the dominant factor to generate the Ekman pumping (Bakun, 1990; Albert et al., 2010), the mesoscale SST-wind stress coupling has a great infl uence on the current dynamic system in this region. On the other hand, the mesoscale SST-wind stress coupling can afference ect the ocean mesoscale eddies which can infl uence the intense biological activity (Spall, 2007; Gruber et al., 2011; Gaube et al, 2015), so that the mesoscale SST-wind stress coupling feedback also has important ecosystem implication in this region. However, the mesoscale SST-wind stress coupling cannot be well simulated in the most current climate models and the regional ocean models when they are forced by prescribed wind and heat fl ux (Bryan et al., 2010). Subsequently, the feedback efference ects of the mesoscale coupling onto the ocean are not taken into account in these models adequately. This may be one of the reasons why there is a consistent warm SST bias in this region in the climate model simulations (Zuidema et al., 2016; Zhu and Zhang, 2018, 2019). To improve the model performances, it is necessary to develop a useful way to represent WSmesothat is related to SSTmeso.

Specifi cally, we exploit an empirical way to depict WSmesobased on the Tikhonov regularization. It can be useful to represent the mesoscale SST-Wind coupling and shed light on a better understanding of mesoscale SST-wind stress coupling feedback on the ocean dynamics. Details about the data and methods are given in Section 2. The observed characteristics of the mesoscale SST-Wind coupling in the western coast of South America are investigated in Section 3.1. The computational examples of reconstructed WSmesoare discussed in Section 3.2. We summarize our fi ndings in Section 4.

2 DATA AND METHOD

2.1 Data

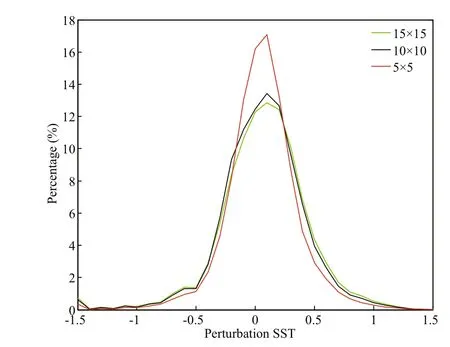
Fig.1 The probability distributions of the mesoscale magnitude of SST perturbations as a function of the difference erent half span parameters calculated in the western coast of South America

The wind stress data used in this study are obtained from Quik Scatterometer (Quik-SCAT, Version4). The SST fi elds are derived from the AMSR-E SST data (Version 7). The Quik-SCAT Scatterometer was launched in June 1999 and operated until November 2009 (Hofference man and Leidner, 2005). The AMSR-E SST data are available from June 2002 to September 2011. In this study, we use the 3-day averaged data during 2003-2008 period. All of the data are obtained from the Asia-Pacifi c Data-Research Center (APDRC) of the University of Hawaii, with the spatial resolution of 0.25°×0.25°.

2.2 LOESS method

The mesoscale air/sea perturbations in the western coast of South America are extracted using a locally weighted regression (LOESS) method (Cleveland and Devlin, 1988). In the LOESS method, the weight equation is a tri-cubic function, and the weight increases as the two points get closer. The maximum intensity of the perturbation fi elds depends on the half-span parameter. Generally, the larger the halfspan parameter is, the larger perturbations we can get. In order to extract the mesoscale perturbation efference ectively in the western coast of South America, we conduct three sensitive experiments with difference erent half-span parameters in the LOESS method. Figure 1 shows the mean probability distributions of SSTmesoduring 2003-2008 from the outputs of the sensitive experiments. The results show that the maximum intensity of SSTmesoincreases with the half-span parameter. However, when the half-span parameter is larger than 10°, the probability distribution of SSTmesois almost the same as that with the half span parameter of 10°. Furthermore, it is found that the coupling coeき cient obtained by the least square fi tting of SSTmesoand WSmesoreaches its maximum when the half span parameters is taken as 10° (not shown). Hence, the half-span parameter is taken as 10° in the LOESS method in this study.

2.3 Tikhonov’s regularization method

The purpose of this study is to calculate the WSmesofrom the Curl(WSmeso) and Div(WSmeso). To solve this problem, the Tikhonov regularization method is used. According to the Helmholtz theorem, the wind stress fi elds can be decomposed to:

in which ψ and χ are the stream function and divergent wind stress potential fi eld, respectively; k is the vertical unit vector. Thus, the curl and divergence of the wind stress fi elds can be reorganized to:

in which ATis the transpose of A. Note that for the limited irregular domain, the solution may be not unique because the computation is complicated at the boundaries (Lynch, 1989). Besides, the matrix A may be ill conditioned or singular irreversible, leading to an infi nite number of solutions for this problem. In these cases, the ill-posed problem can be solved efference ectively with the Tikhonov’s regularization (Tikhonov and Arsenin, 1977). Based on the Tikhonov’s regularization, the solution is:

in which I is the unit matrix; α is the regularization parameter. It has been found that the solution error would be rather small and acceptable when α was within the reasonable range. The α used in this study is 1.0e-6.

Li et al. (2006) computed the ocean current stream function and velocity potential from the velocity vectors by applying the regularized Tikhonov minimization procedure to the ROMS model. They found that the velocity vectors computed from the reconstructed stream function and velocity potential are almost the same as the observation. The difference erences between the reconstructed velocity and observation were smaller than 0.005 m/s, and the overall error was less than 1% of the observed velocity and especially small near the boundaries, which suggested that the Tikhonov method worked well at the boundary. Wei et al. (2019) also showed inverse method can produces reasonably consistent solutions compared to the one established based on the empirical relationship between WSmesoand SSTmesoin the Kuroshio Extension.

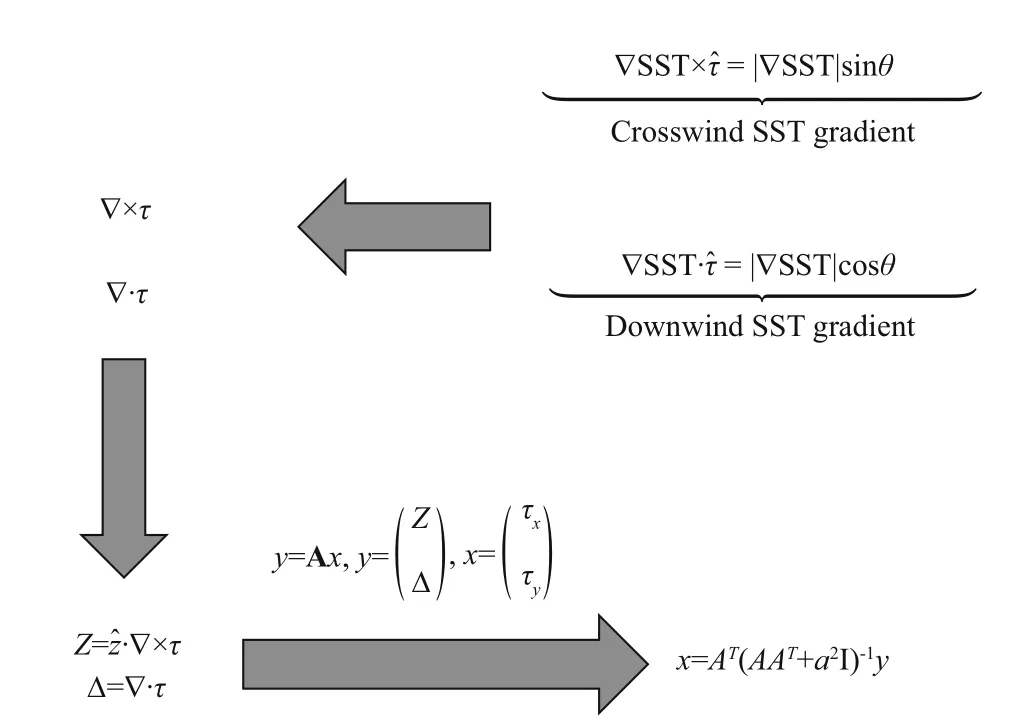
Fig.2 A sketch of procedure in calculating wind stress perturbation response to SST perturbations using the Tikhonov regularization method

Figure 2 shows the calculation process of WSmesowith the Tikhonov regularization method, which can be summarized as follows. First, as indicated by Chelton et al. (2004), the coupling coeき cient between Div(WSmeso) (Curl(WSmeso)) and ∇downSSTmeso( ∇crossSSTmeso) can be obtained by the least square fi tting of them based on the satellite data (in this study, the coupling coeき cients are varied with month). Second, as long as we have the coupling coeき cients and the SST gradient perturbations, Div(WSmeso) and Curl(WSmeso) can be obtained from SST gradient perturbations. Finally, WSmesocan be derived from Div(WSmeso) and Curl(WSmeso) by using the Tikhonov method.

Although Jin et al. (2009) calculated the wind stress from the related SST using the Tikhonov method, their computational example was in the geographically idealized coastal upwelling system, which did not provide the details of reconstructed WSmesoseparately. Therefore, our study focuses on the computation of the WSmesothat is highly related to SSTmeso.

3 RESULT

3.1 The observed mesoscale SST-wind stress coupling characteristics

Figure 3a shows the spatial patterns of SSTmeso(colors) in April 2007 which are derived from the LOESS fi lter. It indicates that SSTmesocan be well extracted by the LOESS fi lter. The SSTmesofi elds are characterized by the alternating positive and negative bands, and the regions with high SSTmesomagnitude are in the nearshore area. The horizontal distributions of the standard deviation for high pass fi ltered SST are shown in Fig.4a & b. In winter (July-October), the regions with high standard deviation for SSTmesocover the whole area and the magnitude of standard deviation for SSTmesoin the Peru Sea is almost the same as that in the Chile Sea (Fig.4a). In summer (December-February), the regions with high standard deviation for SSTmesoare only in the nearshore area and the magnitude of standard deviation for SSTmesoin the Chile Sea is stronger than that in the Peru Sea (Fig.4b). In both seasons, the standard deviation for SSTmesois small in the south-western part of the study area.

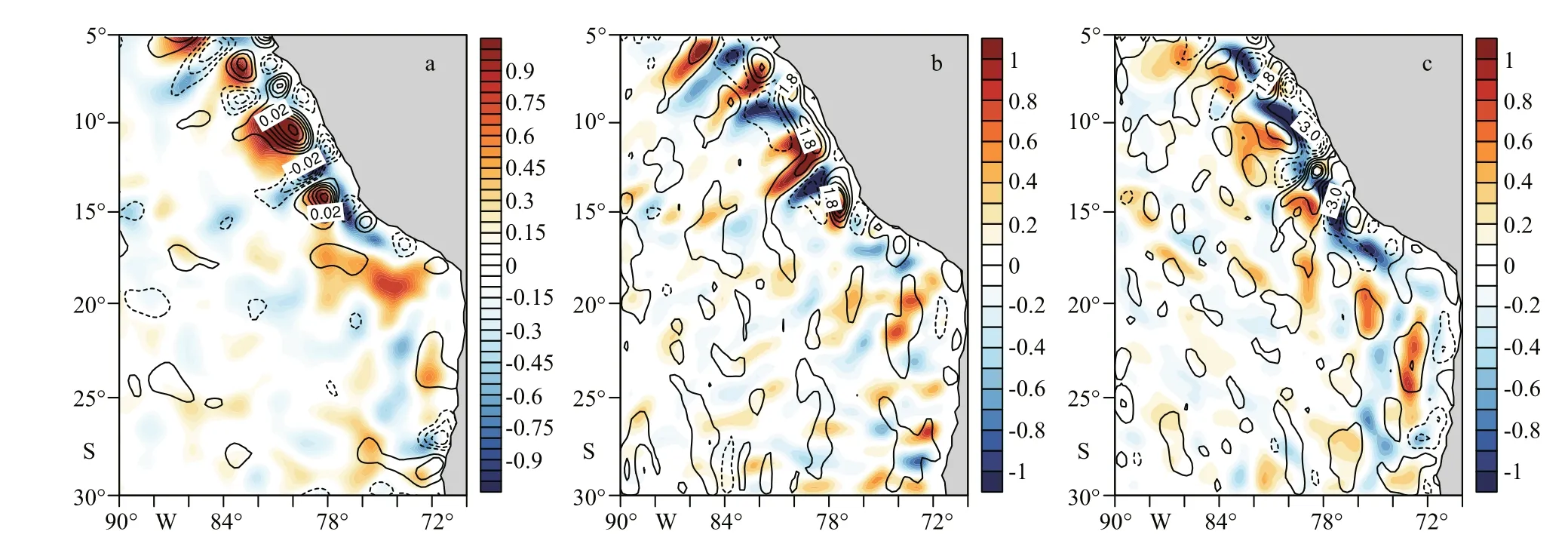
Fig.3 Spatially high pass f iltered wind stress and SST f ield in April 2007

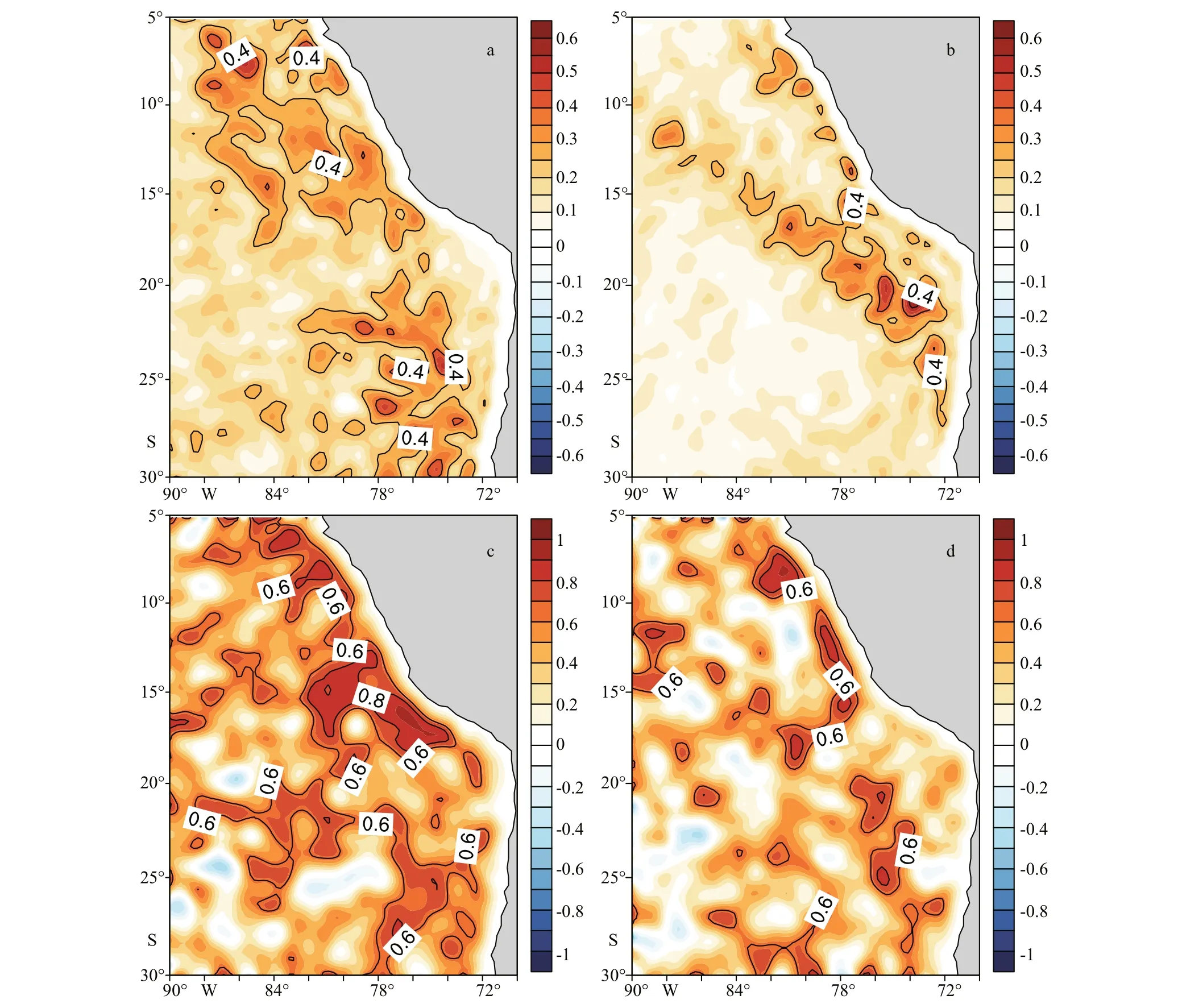
Fig.4 Horizontal distributions of the standard deviation for the high pass fi ltered AMSR-E SST fi elds in winter (a) and summer (b) that averaged during 2003-2008; correlations between the spatially high-pass fi ltered AMSR-E SST and Quik-SCAT wind stress magnitude in winter (c) and summer (d)

The high-pass fi ltered wind stress (contours) also exhibits large perturbation in the western coast of South America (Fig.3a). The pattern of WSmesomagnitude is highly consistent with that of SSTmeso. It is evident that the wind slows down over cooler waters and speeds up over warmer waters. These relations indicate that WSmesomagnitude is positively correlated with SSTmeso. Figure 5 illustrates the timelongitude sections of spatially high pass fi ltered wind stress magnitude (contours) and SST (colors) along 10°S and 11.5°S. It also shows that WSmesomagnitude is positively correlated with SSTmeso. The regions with strong SSTmesoand WSmesocan stretch for a few hundred kilometers away from the shore. The relationships between SSTmesoand WSmesoare further quantifi ed by the correlation analysis based on the satellite data during 2003-2008 (Fig.4c & d). It shows that there is strong correlation between SSTmesoand WSmeso. The correlation patterns between SSTmesoand WSmesoare highly consistent with the patterns of standard deviation for SSTmeso(Fig.4a & b). The regions where WSmesoand SSTmesohave high correlation are in the nearshore area in winter and the spatially averaged correlation in winter is higher than that in summer. The reason why there is higher correlation in winter may be that there is stronger wind and upwelling in Peru Sea in winter (Colas et al., 2012), which generates more mesoscale eddies.

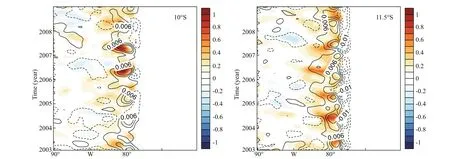
Fig.5 Time-longitude sections of the Quik-SCAT high pass fi ltered wind stress magnitude (contours) and AMSR-E SST (colors) along 10°S and 11.5°S

In addition to WSmesoand SSTmeso, the Div(WSmeso) (Curl(WSmeso)) is also positively correlated with ∇downSSTmeso( ∇crossSSTmeso) (Fig.3b & c). The regions with large Div(WSmeso) and ∇downSSTmesoare in the nearshore area in April 2007 (Fig.3b). The patterns of Div(WSmeso) and ∇downSSTmesodo not match very well, which may be caused by the downward momentum transport in the atmosphere and the sea level pressure adjustment. The downward momentum transport in the atmosphere and the sea level pressure adjustment are two mechanisms explaining the WSmesoresponse to SSTmeso, but the two processes have difference erent efference ects on the distribution of Div(WSmeso) (Frenger et al., 2013). Specifi cally, corresponding to a monopole pattern of SSTmeso, a monopole pattern of Div(WSmeso) is induced when the pressure adjustment mechanism dominates. However, a dipole pattern of Div(WSmeso) is induced when the downward momentum transport mechanism dominates. Oerder et al. (2016) have indicated that although the mesoscale coupling was mainly forced by downward momentum transport mechanism, the near-surface pressure gradient anomalies also had a non-negligible contribution to the mesoscale coupling in the western coast of South America. Therefore, both the two mechanisms need to be considered to explain the WSmesoresponse to SSTmesoin the western coast of South America and afference ect the distribution of Div(WSmeso). As shown in Fig.3c, the ∇crossSSTmesois strong in the nearshore area of the Peru Sea. Because the wind stress curl is an important factor to induce the upwelling and is afference ected by ∇crossSSTmeso, the Ekman upwelling may be strongly infl uenced by the mesoscale SST-wind stress coupling in the western coast of South America.

Analyses have shown that there is strong mesoscale coupling in the western coast of South America, especially in the nearshore region. Figure 6 shows the scatterplots of WSmesomagnitude, Div(WSmeso) and Curl(WSmeso) binned by the ranges of SSTmeso, ∇downSSTmesoand ∇crossSSTmeso, respectively. The coupling coeき cients are obtained from the daily data during 2003-2008. Because the mesoscale SST-wind stress coupling is weak in the southwestern part (20°S-30°S, 84°W-90°W) of the western coast of South America, the coupling coeき cients in this region are not included. In Fig.6, the top panels are the results for winter and the bottom panels are for summer; S means the coupling coeき cient; black dots and vertical bars indicate the medians and interquartile ranges (IQR) in each bin. IQR is defi ned by difference erence between the upper and lower quartiles of the perturbed fi eld. As the coupling coeき cient is sensitive to some extreme values, only the central 50% of the data are specifi ed to avoid the infl uences of the extreme values. It shows that there is a linear relationship between SSTmesoand WSmesoclearly (Fig.6), indicating that Div(WSmeso) and Curl(WSmeso) can be obtained from ∇downSSTmesoand ∇crossSSTmeso, respectively. The coupling coeき cient between SSTmesoand WSmesois about 0.009 5 N/(m2∙°C) in winter and 0.008 2 N/(m2∙°C) in summer. The coupling coeき cients between Div(WSmeso) and ∇downSSTmesoare larger than those between Curl(WSmeso) and ∇crossSSTmeso. In all cases, the coupling coeき cients in winter are larger than those in summer. These results are similar to Oerder et al. (2016). However, the coupling coeき cient between Div(WSmeso) and ∇downSSTmesoin summer is larger than that in their results, which may be caused by the difference erences in fi lter method, study area, and the SST data used in the analyses.

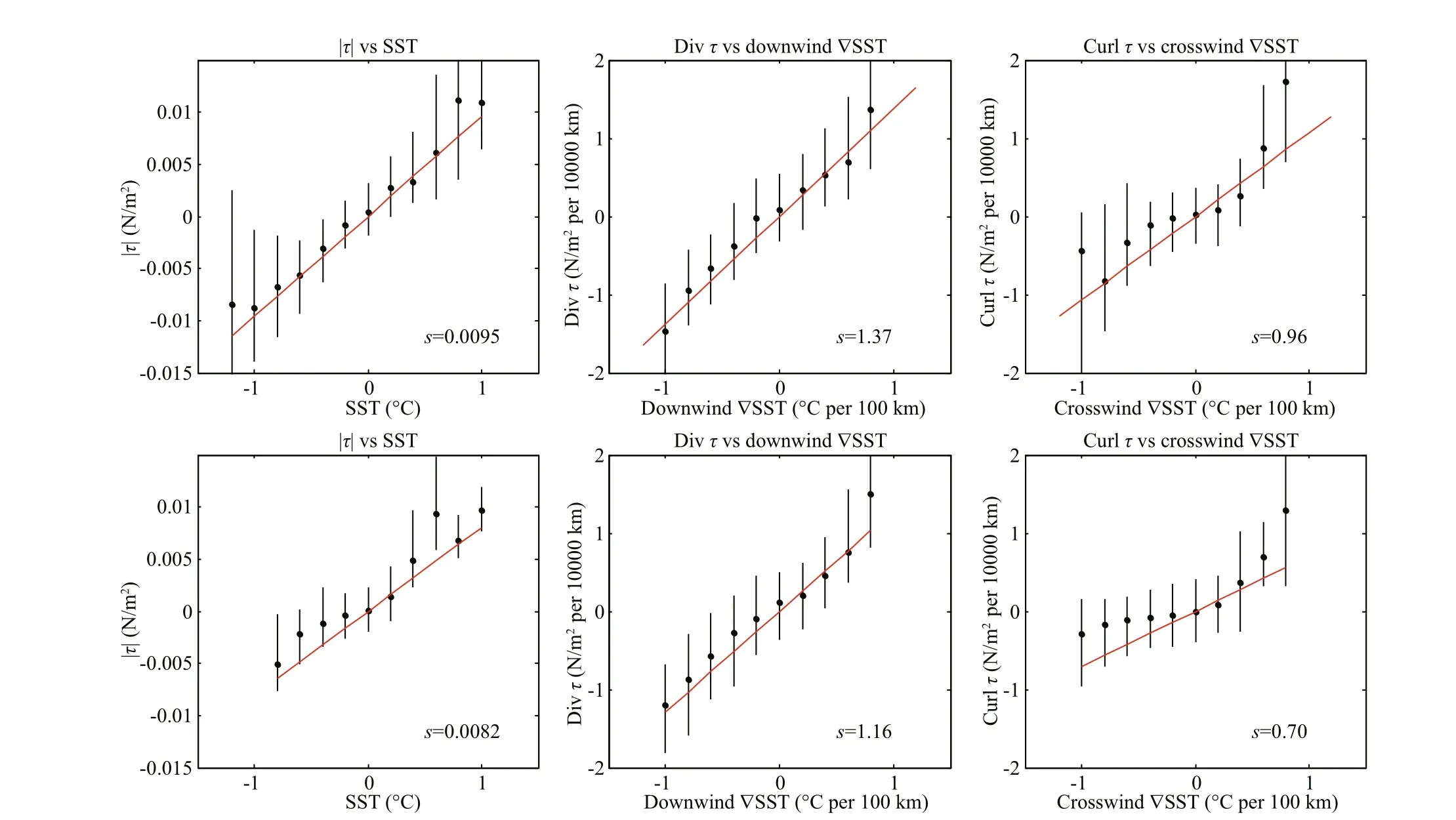
Fig.6 Scatterplots of the spatially high pass fi ltered Quik-SCAT wind stress binned by ranges of AMSR-E SST perturbations for (top) winter and (bottom) summer

The horizontal distributions of coupling coeき cients between SSTmesoand WSmesoin summer and winter are shown in Fig.7 (The unit of coupling coeき cients is N/(m2∙100°C). The distributions of coupling coeき cients are highly consistent with correlations between the spatially high pass fi ltered SST and wind stress magnitude (Fig.4c & d). Both in winter and summer, the regions with high coupling coeき cients are in the nearshore area. There are also some special regions with negative coupling coeき cients in summer in the northern part of Peru Sea. Figure 8 displays the time series of coupling coeき cients between the spatially high pass fi ltered Quik-SCAT wind stress magnitude and AMSR-E SST, wind stress divergence and downwind SST gradient, and wind stress curl and crosswind SST gradient. It is clear that the three coeき cients all exhibit the consistent seasonal variability. The maximum coupling coeき cient between SSTmesoand WSmesoappeared in autumn in year 2003, 2006, and 2007 and winter in year 2004, 2005 and 2008.

Clearly, there is strong mesoscale SST-wind stress coupling in the western coast of South America. However, the mesoscale SST-wind stress coupling processes in these regions cannot be well simulated in most climate models, and the regional ocean models when they are directly forced by prescribed wind and heat fl ux. Thus, the efference ects of the mesoscale coupling to the ocean may have not been taken into account adequately in these models. It is necessary to develop a method to represent WSmesoin response to SSTmesoefference ectively.

3.2 The computational examples

In order to calculate the zonal and meridional components of WSmeso, the Tikhonov’s regularization method is applied in this study with the computational procedure summarized in Section 2.

Fig.7 Horizontal distributions of the coupling coeき cient between the spatially high-pass fi ltered AMSR-E SST and Quik-SCAT wind stress magnitude in winter (a) and summer (b)

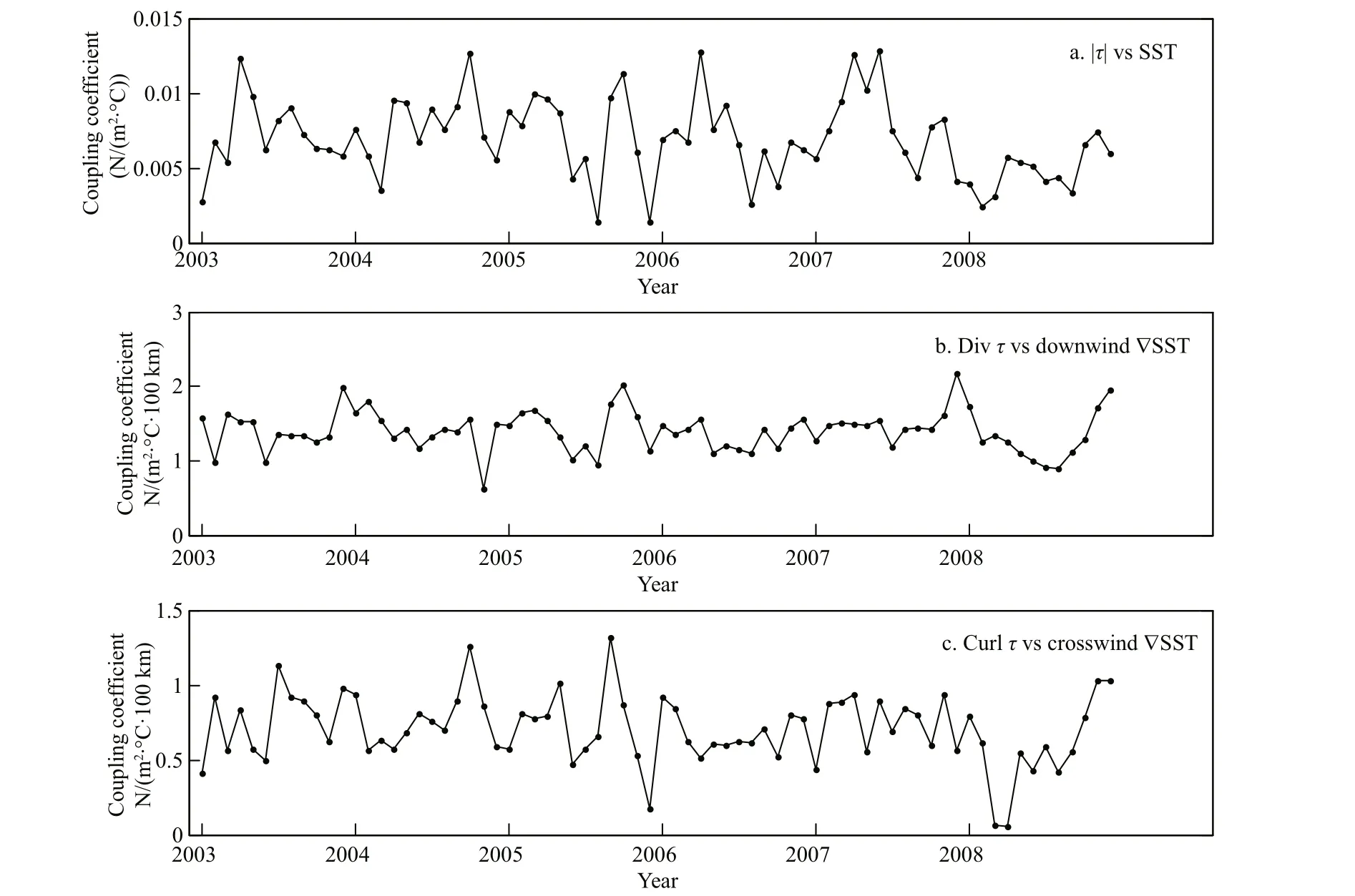
Fig.8 The time series of the coupling coeき cient during 2003-2008 for the spatially high-pass fi ltered Quik-SCAT wind stress magnitude and AMSR-E SST (a); wind stress divergence and downwind SST gradient (b); and wind stress curl and crosswind SST gradient (c)

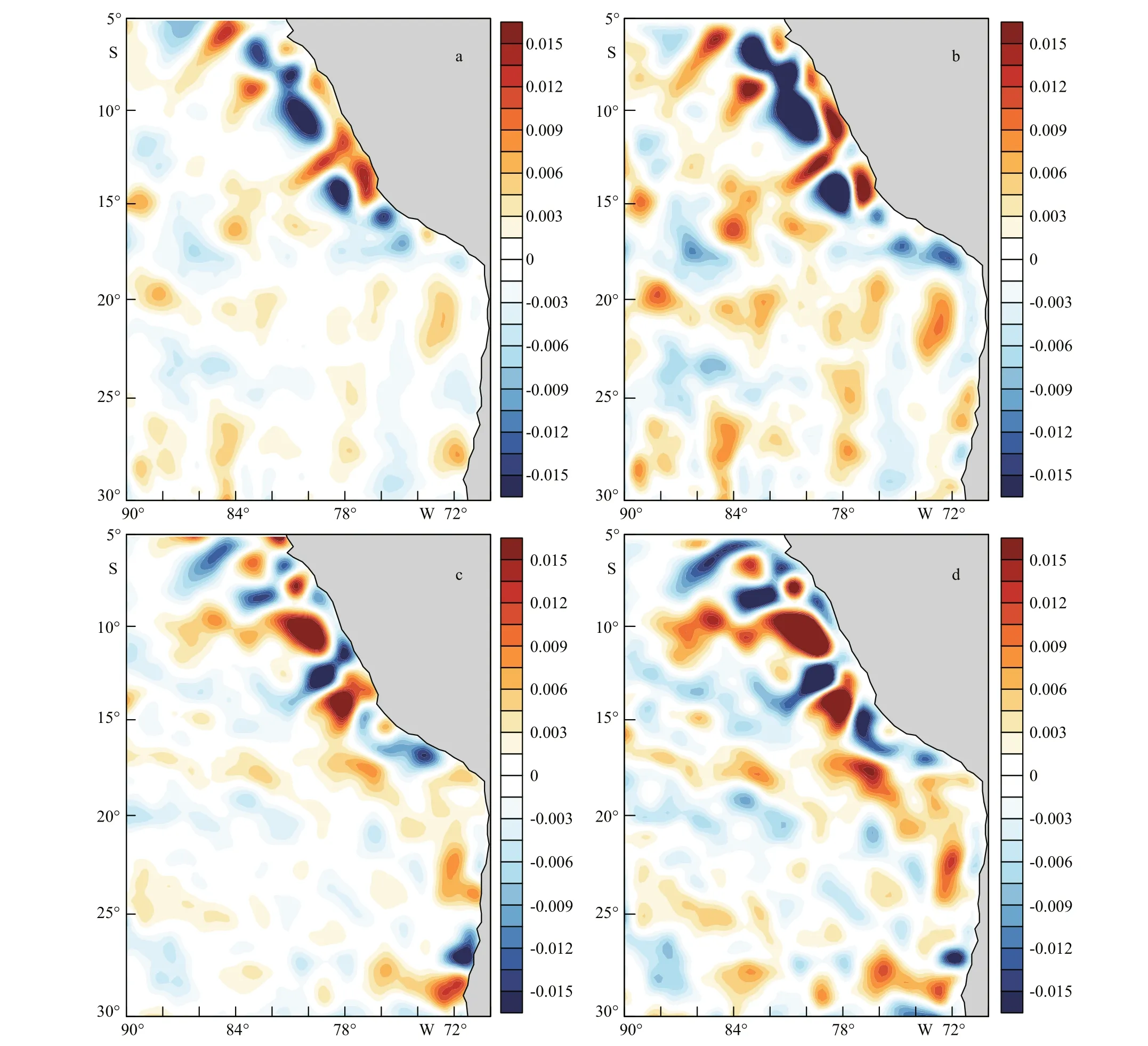
Fig.9 The distributions of wind stress perturbations in April 2007

To verify the reliability of the Tikhonov’s regularization method in the real cases, the WSmesocalculated from Div(WSmeso) and Curl(WSmeso) is compared with the WSmesooriginally obtained from the high pass fi ltered wind stress. For convenience, Div(WSmeso) and Curl(WSmeso) used in the verifi cation are directly derived from the Quik-SCAT wind data. An example is shown in Fig.9. The left panels are the spatially high pass fi ltered Quik-SCAT zonal and meridional wind stress in April 2007. The right panels are the reconstructed zonal and meridional WSmesowhich are derived from the observed Div(WSmeso) and Curl(WSmeso) in April 2007. It shows that the patterns of reconstructed WSmesoare highly consistent with the original WSmeso. The regions with relatively large error are mainly in the nearshore area, but the overall error is less than the 1% of the observed WSmeso, indicating that the Tikhonov’s regularization method is an accurate way to compute WSmesofrom Div(WSmeso) and Curl(WSmeso). We have also tried to use the SVD method to represent WSmeso, but the results (not show) are not as good as that of the LOESS and Tikhonov regularization method in the west coast of South America.

So far, the reliability of this Tikhonov regularization method has been verifi ed. Based on this method, we reconstruct WSmesofrom ∇downSSTmesoand ∇crossSSTmesoin April 2007. The results (not shown) indicate that the magnitude of reconstructed WSmesois weaker than the observed WSmeso. The error may be related to the coupling relationships between Div(WSmeso) (Curl(WSmeso)) and ∇downSSTmeso( ∇crossSSTmeso), which are gained from the observed data. As the coupling coeき cients are obtained from the linear regression method with daily data during years, the coupling coeき cients may be underestimated in some regions. Besides, the Tikhonov regularization parameter may also induce small errors to the results. Both reasons mentioned above may lead to the weak magnitude of reconstructed WSmeso.

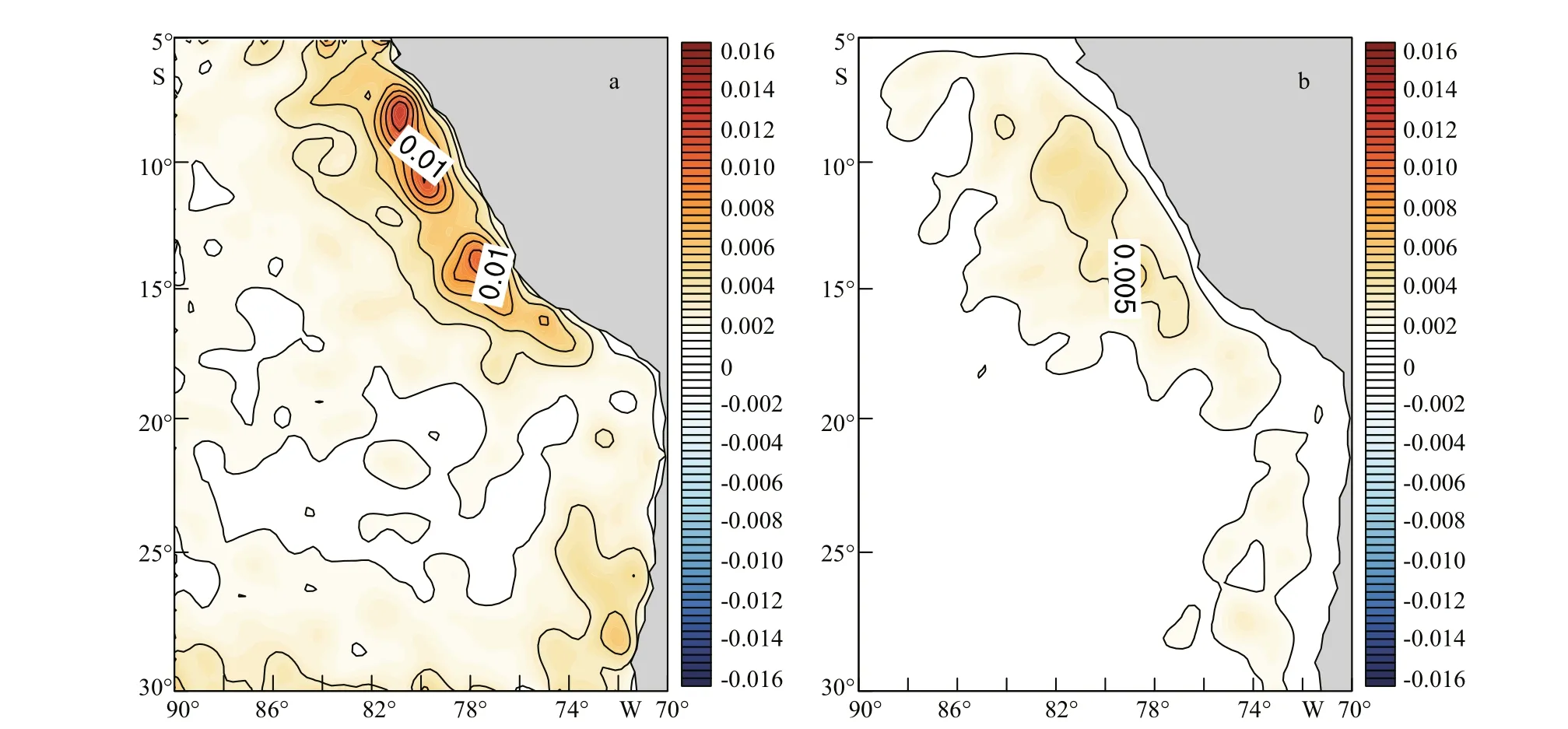
Fig.10 Horizontal distributions of the standard deviation for the Quik-SCAT wind stress magnitude perturbations during 2003-2008 (a); the reconstructed wind stress magnitude perturbations (b)

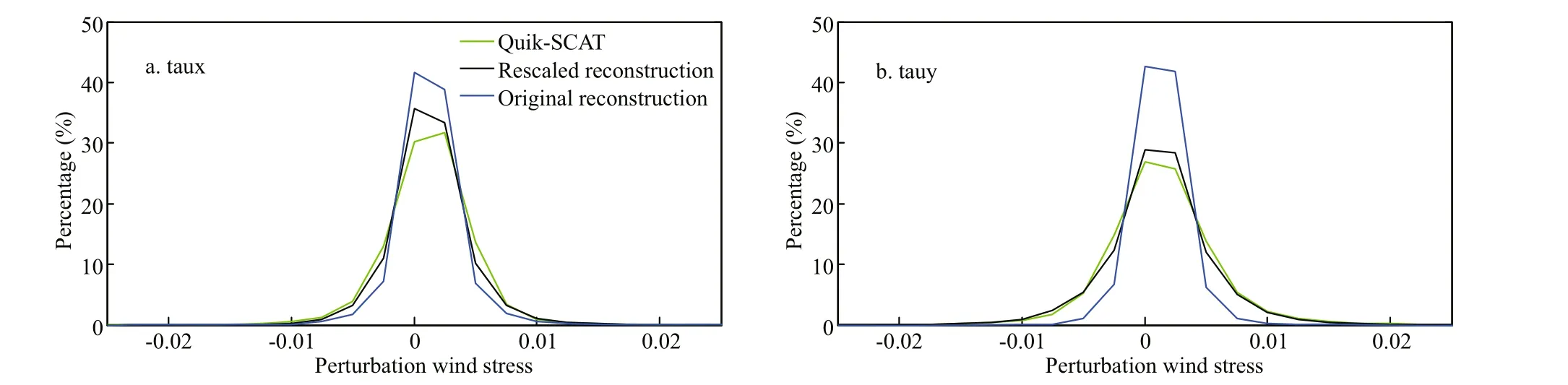
Fig.11 The probability distributions of the mesoscale perturbations of zonal (a) and meridional (b) wind stress during 2003-2008

To reduce the error caused by the coupling relationships, it is necessary to make a correction to the reconstructed WSmeso. The standard deviations of the observed and reconstructed WSmesomagnitudes during 2003-2008 are calculated (Fig.10). The regions where the standard deviations of the reconstructed and observed WSmesohave high values are both in the nearshore area of Peru Sea, and the spatially averaged maximum standard deviation in the observations is almost 2.2 times larger than that in the reconstructed WSmeso. To rescale the reconstructed WSmesomagnitude back to the corresponding observations, the magnitude of reconstructed WSmesois multiplied by 2.2. With this correction, the magnitude of new reconstructed WSmesoderived from ∇downSSTmesoand ∇crossSSTmesois closer to the observations. The probability distributions of the original, rescaled reconstructed WSmesoand observed WSmesoare calculated and averaged with daily data from 2003 to 2008 (Fig.11). It shows that the probability distributions of the rescaled reconstructed WSmesoare highly similar to those of the observed WSmeso. The new reconstructed WSmesoderived from ∇downSSTmesoand ∇crossSSTmesoin April 2007 is displayed in Fig.12. It shows that the magnitude of reconstructed WSmesois comparable to the observed WSmeso(Fig.9a & c), and the patterns of reconstructed WSmesoare highly consistent with those of the observed WSmeso. By comparing with the patterns of SSTmesoin April 2007 (shown in Fig.3a), it is found that the patterns of reconstructed WSmesoare highly consistent with those of SSTmeso, indicating that WSmesocan be well represented by the Tikhonov regularization method. The regions with relative high difference erence between reconstructed wind stress perturbations and observation are mainly in the nearshore area.

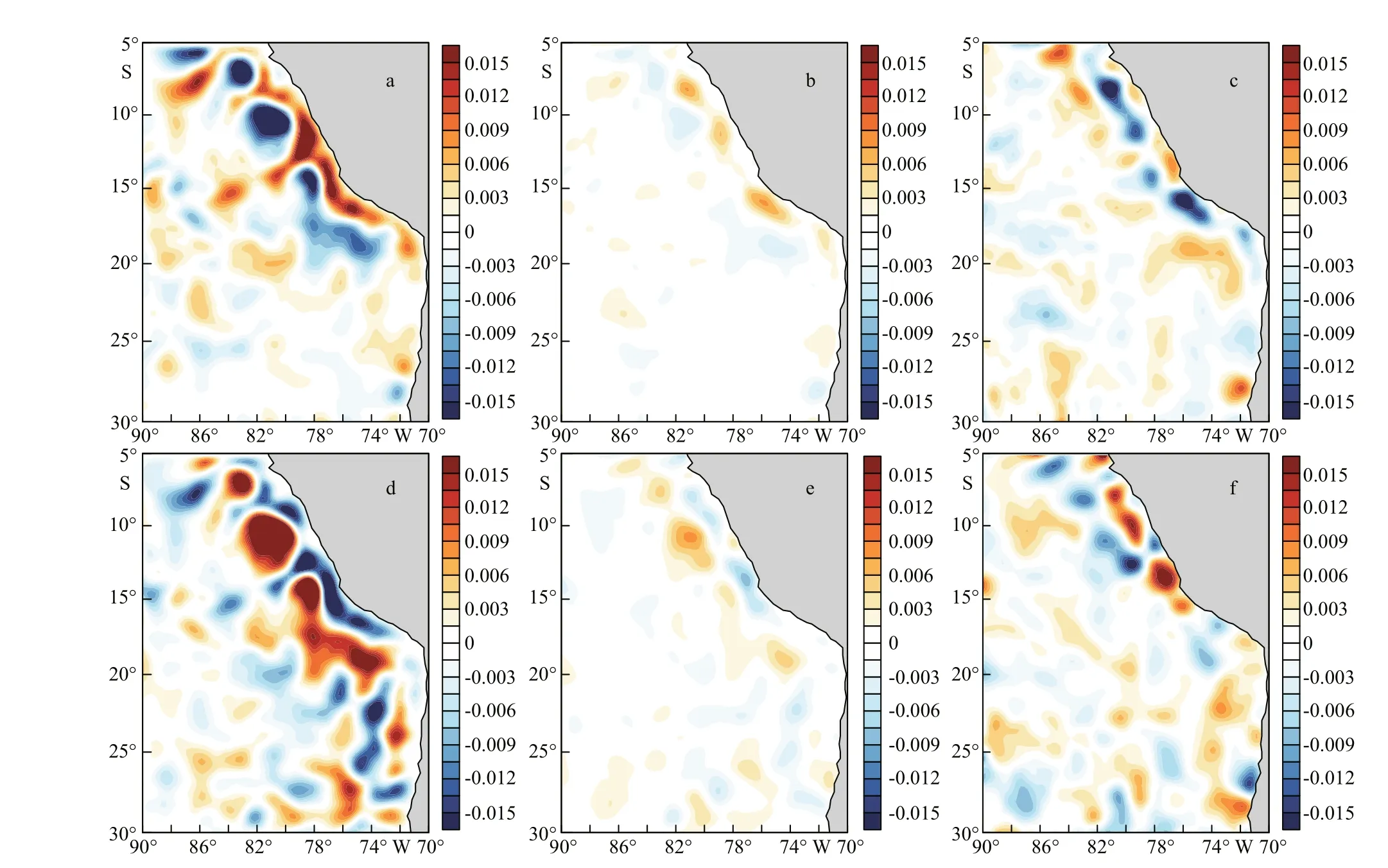
Fig.12 The distributions of wind stress perturbations in April 2007

Another example is shown for February 2005 (Fig.13). The results show that the patterns of reconstructed WSmesoare almost consistent with those of the observed WSmeso. Meanwhile, the main characteristics of the observed WSmesocan also be well represented by the Tikhonov regularization method, especially in the nearshore regions. In general, the Tikhonov regularization method is an efference ective way to represent WSmesoin response to SSTmeso. Furthermore, the meridional and zonal WSmesocan be separately calculated, which is another important advantage of using this method.

4 DISCUSSION AND SUMMARY

In this work, the relationship between SSTmesoand WSmesoin the western coast of South America is quantifi ed based on satellite data. To extract the mesoscale perturbation fi eld, a locally weighted regression (LOESS) method with the half-span parameter of 10° is used. The results show that the mesoscale perturbations of wind stress, wind stress divergence, and wind stress curl are positively correlated with the high pass fi ltered SST, downwind SST gradients, and crosswind SST gradients, respectively. The coupling coeき cient between SSTmesoand WSmesois about 0.009 5 N/(m2∙°C) in winter and 0.008 2 N/(m2∙°C) in summer. According to the horizontal distributions of the coupling coeき cient between SSTmesoand WSmeso, it is found that the mesoscale coupling is strong in the nearshore area. The time series of three mesoscale coupling coeき cients show the consistent seasonal variability and indicate that the stronger mesoscale SST-wind stress coupling in winter and autumn. All the results indicate that there is strong mesoscale SST-wind stress coupling in the western coast of South America. However, the mesoscale SST-wind stress coupling in these regions cannot be well simulated in many models currently used (Bryan et al., 2010). It is necessary to develop an efference ective method to represent WSmesoin response to SSTmeso.

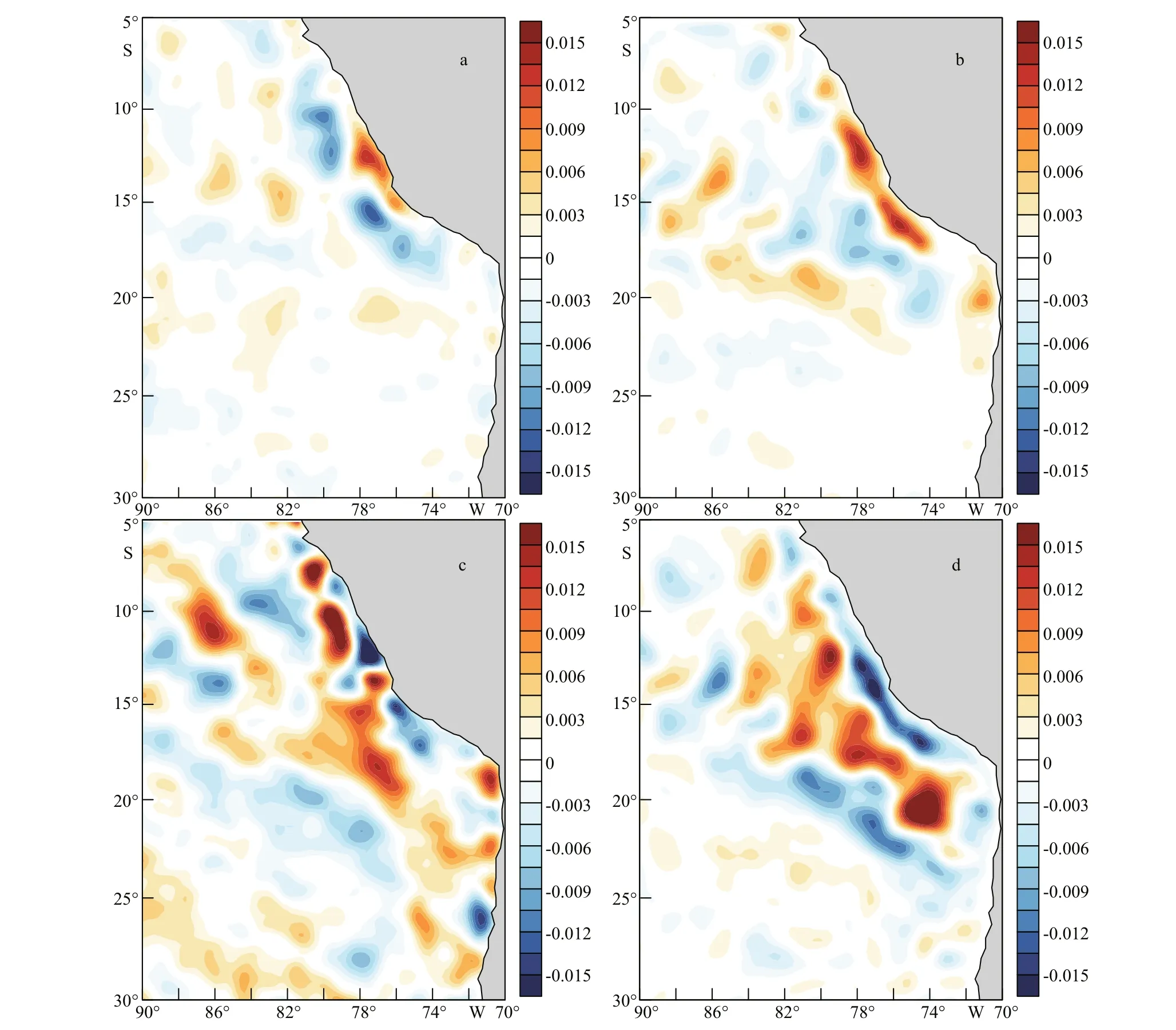
Fig.13 The distributions of wind stress perturbations in February 2005

The Tikhonov regularization method is used to compute WSmesoas a response to SSTmesoin this study. Based on the observed coupling coeき cient between Div(WSmeso) (Curl(WSmeso)) and ∇downSSTmeso( ∇crossSSTmeso), Div(WSmeso) and Curl(WSmeso) can be obtained from ∇downSSTmesoand ∇crossSSTmeso. Then, WSmesocan be calculated from Div(WSmeso) and Curl(WSmeso) with the Tikhonov regularization method. Results indicate there is a large difference erence between the magnitude of reconstructed WSmesoand observations when the coupling coeき cients are obtained with daily data during 2003-2008. By comparing the spatially averaged standard deviations of reconstructed WSmesomagnitude and observations, it is found that a reasonable magnitude of WSmesocan be obtained when a rescaling factor of 2.2 is used. With the Tikhonov regularization method, the meridional and zonal WSmesocan also be calculated separately. Furthermore, the patterns of the reconstructed WSmesoare highly consistent with SSTmeso, indicating that the Tikhonov regularization method is a useful way to represent WSmesoin response to SSTmeso.

Although the computational applications of the Tikhonov regularization method in this study are located in the western coast of South America, this method can be applicable to any regions and useful for a variety of applications. One important application is to improve large-scale ocean model simulation, a similar way used in the TIW-induced wind feedback studies (Zhang and Busalacchi, 2008; Zhang, 2016). By using the Tikhonov regularization method to calculate WSmesofi eld, ocean models can be forced by the reconstructed WSmesoas well as the prescribed wind stress and heat fl ux. Thus, the feedback of the mesoscale air-sea coupling on the ocean can be included in the ocean model simulation, which would improve the ocean model simulation skills. Other applications include the studies on the mesoscale SST-wind coupling in any region. As the atmospheric processes are very complicated, it is diき cult to well simulate the atmospheric wind response to SSTmesoin the climate models. The Tikhonov regularization method can be used to reconstruct the WSmesoin response to SSTmesoefference ectively . Thus, the feedback of the mesoscale SST-wind stress coupling on the ocean dynamics can be taken into account. Furthermore, these applications can shed light on a better understanding of the physical processes that are involved in the mesoscale SST-wind coupling.

For example, in the western coast of South America, there is a systematic warm SST bias in the climate model (Zuidema et al., 2016; Zhu and Zhang, 2018, 2019). According to the previous work, it might be caused by too little stratus cloud cover in the model simulations, and so an excessive amount of solar radiation reached the sea surface (Davey et al., 2002; Meehl et al., 2005). Besides, the warm SST bias could also be caused by the mesoscale interaction which is not adequately represented in the model simulations (Penven et al., 2005). All these studies do not take into account the efference ect of the mesoscale SST-wind stress coupling on the ocean. As the wind stress curl is an important factor inducing the upwelling and can be modifi ed by the mesoscale SST gradients, the Ekman upwelling would be infl uenced by the mesoscale SSTwind stress coupling in the regions with strong SSTmesosignals. As has been demonstrated before, the simulated coupling coeき cient between WSmesoand SSTmesois weaker than observations in this region (Bryan et al., 2010). Then, the magnitude of Ekman pumping may be underestimated with less cold waters being pumped to the sea surface. Therefore, it is necessary to develop a way to represent mesoscale SST-wind stress coupling in the models to reduce the warm SST bias. With the Tikhonov regularization method, we can adequately calculate WSmesoin response to SSTmeso. This method allows us to study the feedback of the mesoscale SST-wind stress coupling on the ocean efference ectively and helps us to improve the model simulations, which will be examined in the future.

5 DATA AVAILABILITY STATEMENT

All of the data are obtained from the Asia-Pacifi c Data-Research Center (APDRC) of the University of Hawaii which is available at http://apdrc.soest.hawaii.edu/las/v6/dataset?catitem=1 .

6 ACKNOWLEDGMENT

The authors wish to thank the anonymous reviewers for their numerous comments that helped to improve the original manuscript.

References

Albert A, Echevin V, Lévy M, Aumont O. 2010. Impact of nearshore wind stress curl on coastal circulation and primary productivity in the Peru upwelling system. J. Geophys. Res., 115(C12): C12033, https://doi.org/10. 1029/2010JC006569.

Bakun A. 1990. Global climate change and intensifi cation of coastal ocean upwelling. Science, 247(4939): 198-201, https://doi.org/10.1126/science.247.4939.198.

Bourras D, Reverdin G, Giordani H, Caniaux G. 2004. Response of the atmospheric boundary layer to a mesoscale oceanic eddy in the northeast Atlantic. J. Geophys. Res., 109(D18): D18114, https://doi.org/10.1029/2004JD004799.

Bryan F O, Tomas R, Dennis J M, Chelton D B, Loeb N G, McClean J L. 2010. Frontal scale air-sea interaction in high-resolution coupled climate models. J. Climate, 23(23): 6 277-6 291, https://doi.org/10.1175/2010JCLI3665.1.

Businger J A, Shaw W J. 1984. The response of the marine boundary layer to mesoscale variations in sea-surface temperature. Dyn. Atmos. Oceans, 8(3-4): 267-281, https://doi.org/10.1016/0377-0265(84)90012-5.

Capet X, Colas F, McWilliams J C, Penven P, Marchesiello P. 2008. Eddies in eastern boundary subtropical upwelling systems. In: Hecht M W, Hasumi H eds. Ocean Modeling in an Eddying Regime, Volume 177. American Geophysical Union, Washington. 350p, https://doi.org/10. 1029/177GM10.

Castelao R M. 2012. Sea surface temperature and wind stress curl variability near a cape. J. Phys. Oceanogr., 42(11): 2 073-2 087, https://doi.org/10.1175/JPO-D-11-0224.1.

Chelton D B, Esbensen S K, Schlax M G, Thum N, Freilich M H, Wentz F J, Gentemann C L, McPhaden M J, Schopf P S. 2001. Observations of coupling between surface wind stress and sea surface temperature in the eastern tropical pacifi c. J. Climate, 14(7): 1 479-1 498, https://doi.org/10.1175/1520-0442(2001)014＜1479:OOCBSW＞2.0.CO;2.

Chelton D B, Schlax M G, Freilich M H, Millifference R F. 2004. Satellite measurements reveal persistent small-scale features in ocean winds. Science, 303(5660): 978-983, https://doi.org/10.1126/science.1091901.

Chelton D B, Schlax M G, Samelson R M. 2007. Summertime coupling between sea surface temperature and wind stress in the California Current System. J. Phys. Oceanogr., 37(3): 495-517, https://doi.org/10.1175/JPO3025.1.

Chelton D B, Xie S P. 2010. Coupled ocean-atmosphere interaction at oceanic mesoscales. Oceanography, 23(4): 52-69, https://doi.org/10.5670/oceanog.2010.05.

Cleveland W S, Devlin S J. 1988. Locally weighted regression: an approach to regression analysis by local fi tting. J. Am. Stat. Assoc., 83(403): 596-610, https://doi.org/10.2307/2289282.

Colas F, McWilliams J C, Capet X, Kurian J. 2012. Heat balance and eddies in the Peru-Chile current system. Climate Dyn., 39(1-2): 509-529, https://doi.org/10.1007/s00382-011-1170-6.

Davey M, Huddleston M, Sperber K, Braconnot P, Bryan F, Chen D, Colman R, Cooper C, Cubasch U, Delecluse P, DeWitt D, Fairhead L, Flato G, Gordon C, Hogan T, Ji M, Kimoto M, Kitoh A, Knutson T, Latif M, Treut Le H, Li T, Manabe S, Mechoso C, Power S, Roeckner E, Terray L, Vintzileos A, Voss R, Wang B, Washington W, Yoshikawa I, Yu J, Yukimoto S, Zebiak S, Meehl G. 2002. STOIC: a study of coupled model climatology and variability in tropical ocean regions. Climate Dyn., 18(5): 403-420, https://doi.org/10.1007/s00382-001-0188-6.

Frenger I, Gruber N, Knutti R, Münnich M. 2013. Imprint of Southern Ocean eddies on winds, clouds and rainfall. Nat. Geosci., 6(8): 608-612. https://doi.org/10.1038/ngeo1863.

Gao J X, Zhang R H, Wang H N. 2019. Mesoscale SST perturbation-induced impacts on climatological precipitation in the Kuroshio-Oyashio extension region, as revealed by the WRF simulations. J. Oceanol. Limnol., 37(2): 385-397, https://doi.org/10.1007/s00343-019-8065-5.

Gaube P, Chelton D B, Samelson R M, Schlax M G, O’Neill L W. 2015. Satellite observations of mesoscale eddyinduced Ekman pumping. J. Phys. Oceanogr., 45(1): 104-132, https://doi.org/10.1175/JPO-D-14-0032.1.

Giordani H, Planton S, Benech B, Kwon B H. 1998. Atmospheric boundary layer response to sea surface temperatures during the SEMAPHORE experiment. J. Geophys. Res., 103(C11): 25 047-25 060, https://doi.org/ 10.1029/98JC00892.

Gruber N, Lachkar Z, Frenzel H, Marchesiello P, Münnich M, McWilliams J C, Nagai T, Plattner G K. 2011. Eddyinduced reduction of biological production in eastern boundary upwelling systems. Nat. Geosci., 4(11): 787-792, https://doi.org/10.1038/ngeo1273.

Hofference man R N, Leidner S M. 2005. An introduction to the nearreal-time QuikSCAT Data. Wea. Forecasting, 20(4): 476-493, https://doi.org/10.1175/WAF841.1.

Jin X, Dong C M, Kurian J, McWilliams J C, Chelton D B, Li Z J. 2009. SST-wind interaction in coastal upwelling: oceanic simulation with empirical coupling. J. Phys. Oceanogr., 39(11): 2 957-2 970, https://doi.org/10.1175/ 2009JPO4205.1.

Li Z J, Chao Y, McWilliams J C. 2006. Computation of the streamfunction and velocity potential for limited and irregular domains. Mon. Wea. Rev., 134(11): 3 384-3 394, https://doi.org/10.1175/MWR3249.1.

Lynch P. 1989. Partitioning the wind in a limited domain. Mon. Wea. Rev., 117(7): 1 492-1 500, https://doi.org/10.1175/1520-0493(1989)117＜1492:PTWIAL＞2.0.CO;2.

Ma X H, Jing Z, Chang P, Liu X, Montuoro R, Small R J, Bryan F O, Greatbatch R J, Brandt P, Wu D X, Lin X P, Wu L X. 2016. Western boundary currents regulated by interaction between ocean eddies and the atmosphere. Nature, 535(7613): 533-537, https://doi.org/10.1038/nature18640.

Meehl G A, Covey C, McAvaney B, Latif M, Stoufference er R J. 2005. Overview of the coupled model intercomparison project. Bull. Amer. Meteor. Soc., 86: 89-93.

Minobe S, Kuwano-Yoshida A, Komori N, Xie S P, Small R J. 2008. Infl uence of the Gulf Stream on the troposphere. Nature, 452(7184): 206-209, https://doi.org/10.1038/nature06690.

O’Neill L W, Chelton D B, Esbensen S K, Wentz F J. 2005. High-resolution satellite measurements of the atmospheric boundary layer response to SST variations along the Agulhas return current. J. Climate, 18(14): 2 706-2 723, https://doi.org/10.1175/JCLI3415.1.

O’Neill L W, Chelton D B, Esbensen S K. 2010a. The efference ects of SST-induced surface wind speed and direction gradients on midlatitude surface vorticity and divergence. J. Climate, 23(2): 255-281, https://doi.org/10.1175/ 2009JCLI2613.1.

O’Neill L W, Chelton D B, Esbensen S K. 2012. Covariability of surface wind and stress responses to sea surface temperature fronts. J. Climate, 25(17): 5 916-5 942, https://doi.org/10.1175/JCLI-D-11-00230.1.

O’Neill L W, Esbensen S K, Thum N, Samelson R M, Chelton D B. 2010b. Dynamical analysis of the boundary layer and surface wind responses to mesoscale SST perturbations. J. Climate, 23(3): 559-581, https://doi.org/10.1175/2009JCLI2662.1.

O’Neill L W. 2012. Wind speed and stability efference ects on coupling between surface wind stress and SST observed from buoys and satellite. J. Climate, 25(5): 1 544-1 569, https://doi.org/10.1175/JCLI-D-11-00121.1.

Oerder V, Colas F, Echevin V, Masson S, Hourdin C, Jullien S, Madec G, Lemarié F. 2016. Mesoscale SST-wind stress coupling in the Peru-Chile current system: which mechanisms drive its seasonal variability? Climate Dyn., 47(7-8): 2 309-2 330, https://doi.org/10.1007/s00382-015-2965-7.

Penven P, Echevin V, Pasapera J, Colas F, Tam J. 2005. Average circulation, seasonal cycle, and mesoscale dynamics of the Peru Current System: a modeling approach. J. Geophys. Res., 110(C10): C10021, https://doi.org/10. 1029/2005JC002945.

Piazza M, Terray L, Boé J, Maisonnave E, Sanchez-Gomez E. 2016. Infl uence of small-scale North Atlantic sea surface temperature patterns on the marine boundary layer and free troposphere: a study using the atmospheric ARPEGE model. Climate Dyn., 46(5-6): 1 699-1 717, https://doi.org/10.1007/s00382-015-2669-z.

Renault L, Molemaker M J, McWilliams J C, Shchepetkin A F, Lemarié F, Chelton D B, Illig S, Hall A. 2016. Modulation of wind work by oceanic current interaction with the atmosphere. J. Phys. Oceanogr., 46(6): 1 685-1 704, https://doi.org/10.1175/JPO-D-15-0232.1.

Seo H, Miller A J, Norris J R. 2016. Eddy-wind interaction in the California Current System: dynamics and impacts. J. Phys. Oceanogr., 46(2): 439-459, https://doi.org/10.1175/JPO-D-15-0086.1.

Seo H. 2017. Distinct infl uence of air-sea interactions mediated by mesoscale sea surface temperature and surface current in the Arabian Sea. J. Climate, 30(20): 8 061-8 080, https://doi.org/10.1175/JCLI-D-16-0834.1.

Small R J, DeSzoeke S P, Xie S P, O’Neill L, Seo H, Song Q, Cornillon P, Spall M, Minobe S. 2008. Air-sea interaction over ocean fronts and eddies. Dyn. Atmos. Oceans, 45(3-4): 274-319, https://doi.org/10.1016/j.dynatmoce.2008.01.001.

Spall M A. 2007. Efference ect of sea surface temperature-wind stress coupling on baroclinic instability in the ocean. J. Phys. Oceanogr. 37(4): 1 092-1 097, https://doi.org/10.1175/JPO3045.1.

Strub P T, Mesias J M, Montecino V, Rutllant J, Salinas S. 1998. Coastal ocean circulation ofference western South America. In: Robinson A, Brink K eds. The Sea. Wiley, New York. p.29-67.

Sweet W, Fett R, Kerling J, La Violette P. 1981. Air-sea interaction efference ects in the lower troposphere across the north wall of the Gulf-stream. Mon. Wea. Rev., 109(5): 1 042-1 052, https://doi.org/10.1175/1520-0493(1981) 109＜1042:ASIEIT＞2.0.CO;2.

Tikhonov A N, Arsenin V Y. 1977. Solution of Ill-Posed Problems. Winston and Sons, Washington.

Wei Y Z, Wang H N, Zhang R H. 2019. Mesoscale wind stress-SST coupled perturbations in the Kuroshio Extension. Prog. Oceanogr., 172: 108-123, https://doi.org/10.1016/j.pocean.2019.01.012.

Wei Y Z, Zhang R H, Wang H N. 2017. Mesoscale wind stress-SST coupling in the Kuroshio extension and its efference ect on the ocean. J. Oceanogr., 73 (6): 785-798, https://doi.org/10.1007/s10872-017-0432-2.

Xie S P, Philander S G H. 1994. A coupled ocean-atmosphere model of relevance to the ITCZ in the eastern Pacifi c. Tellus A: Dyn. Meteor. Oceanogr., 46(4): 340-350, https://doi.org/10.3402/tellusa.v46i4.15484.

Zhang R H, Busalacchi A J. 2008. Rectifi ed efference ects of tropical instability wave (TIW)-induced atmospheric wind feedback in the tropical Pacifi c. Geophys. Res. Lett., 35(5): L05608, https://doi.org/10.1029/2007GL033028.

Zhang R H, Busalacchi A J. 2009. An empirical model for surface wind stress response to SST forcing induced by tropical instability waves (TIWs) in the eastern equatorial pacifi c. Mon. Wea. Rev., 137(6): 2 021-2 046, https://doi.org/10.1175/2008MWR2712.1.

Zhang R H, Gao C. 2016. The IOCAS intermediate coupled model (IOCAS ICM) and its real-time predictions of the 2015-16 El Niño event. Sci. Bull., 66(13): 1 061-1 070, https://doi.org/10.1007/s11434-016-1064-4.

Zhang R H, Gao C. 2017. Processes involved in the secondyear warming of the 2015 El Niño event as derived from an intermediate ocean model. Sci. China Earth Sci., 60(9): 1 601-1 613, https://doi.org/10.1007/s11430-016-0201-9.

Zhang R H. 2016. A modulating efference ect of Tropical Instability Wave (TIW)-induced surface wind feedback in a hybrid coupled model of the tropical Pacifi c. J. Geophys. Res., 121(10): 7 326-7 353, https://doi.org/10.1002/2015JC011567.

Zhu Y C, Zhang R H. 2018. An Argo-derived background difference usivity parameterization for improved ocean simulations in the tropical Pacifi c. Geophys. Res. Lett., 45(3): 1 509-1 517, https://doi.org/10.1002/2017GL076269.

Zhu Y C, Zhang R H. 2019. A modifi ed vertical mixing parameterization for its improved ocean and coupled simulations in the tropical Pacifi c. J. Phys. Oceanogr., 49(1): 21-37, https://doi.org/10.1175/JPO-D-18-0100.1.

Zuidema P, Chang P, Medeiros B, Kirtman B P, Mechoso R, Schneider E K, Toniazzo T, Richter I, Small R J, Bellomo K, Brandt P, de Szoeke S, Farrar J T, Jung E, Kato S, Li M K, Patricola C, Wang Z Y, Wood R, Xu Z. 2016. Challenges and prospects for reducing coupled climate model SST biases in the eastern tropical Atlantic and Pacifi c oceans. Bull. Amer. Meteor. Soc., 97(12): 2 305-2 327, https://doi.org/10.1175/BAMS-D-15-00274.1.