城市浅埋小净距隧道爆破施工优化与分析
吴波,兰扬斌,杨仕升,王帅帅,代义昌
城市浅埋小净距隧道爆破施工优化与分析
吴波1, 2,兰扬斌1, 2,杨仕升1, 2,王帅帅3,代义昌3
(1. 广西大学 土木建筑工程学院,广西 南宁 530004;2. 广西大学 工程防灾与结构安全教育部重点实验室,广西 南宁 530004;3. 中交第一公路工程有限公司,湖北 武汉 430056)
针对福州地铁2号线洋里站矿山法段爆破施工优化问题,采用数值软件计算不同工况下小净距隧道的力学响应;以左右洞错开距离、爆破开挖进尺、上台阶长度为试验因素,以后行洞右侧拱腰水平位移峰值、中隔岩有效应力峰值、地表振速峰值以及双洞贯通时长为评价指标设计三因素四水平的正交试验;采用灰色关联度分析和组合赋权法进行结果数据处理,并获得最优参数组合。研究结果表明:左右洞错开20 m,爆破开挖进尺3 m,上台阶长度10 m为小净距隧道爆破施工最优化方案,且与现场实际采用的爆破方案对比,隧道中隔岩拱腰水平位移、中隔岩有效应力峰值、地表振速峰值分别降低11.4%,33.7%和12.84%;基于正交试验的灰色关联度分析可以通过少次数的试验获得最优化参数方案,具有良好的应用前景。
小净距;隧道爆破;数值模拟;正交试验;灰色关联分析
进入21世纪以来,我国铁路建设规模持续扩大,尤其是城市轨道交通发展最为迅猛,在地铁隧道里程持续增长的同时,地铁隧道建设的形式越来越多,难度也越来越大,其中浅埋小净距隧道是一个较为典型的例子。在城市地铁建设过程中,难免会遇到较为坚硬的岩体,这时常规的TBM掘进方法满足不了施工要求,便需要进行钻爆法施工。对于城市浅埋小净距隧道爆破施工,如何控制地表振速、隧道稳定性,同时不影响施工进度是值得研究的施工优化问题。目前,国内外对于小净距隧道的研究主要采用数值模拟法、现场监测法、模型试验法和力学解析法等。ZOU等[1]通过数值模拟对浅埋小净距隧道爆破施工对地表振动特性进行了研究,提出了开挖后成洞区对地表振动强度具有放大作用,且放大倍数与爆破掌子面位置有关。凌同华 等[2]通过对分岔隧道过渡段进行实时监测,得出了先行洞在不同监测位置处的振动波传播规律,并结合数值模拟和拟合分析确定了分岔隧道过渡段爆破安全控制标准。Sterpi等[3]将铝棒作为相似材料进行模型试验,以气囊逐步卸压来模拟隧道的逐步开挖过程,研究了单洞和小净距双洞浅埋隧道的破坏状态。苏芳芮[4]通过力学解析法,对小净距隧道围岩应力计算理论和公式进行了完善,提出了小净距隧道的破坏模式构造方法。关于隧道工程中优化问题的研究,目前主要有BP神经网络法、回归分析法、灰色关联度法。田明杰等[5]通过现场试验获取实测数据,并利用BP神经网络对数据进行回归、预测对隧道在施工过程中的稳定性进行评价。苑绍东等[6]通过萨道夫斯基经验公式对现场监测数据进行线性回归,确定了青岛地铁沿线建筑物的安全振速控制标准及范围。Koopialipoor等[7-8]通过ANN法和混合遗传算法两种智能系统对隧道钻爆作业进行预测和控制。Hyun等[9]通过AHP法对盾构掘进机在掘进过程中发生不良事件的潜在风险进行了探。Nezarat等[10]通过FAHP法对隧道机械化掘进的地质风险进行排序,并指出隧道掌子面隧道失稳的概率最高。本文针对城市浅埋小净距隧道爆破施工过程中遇到的问题,如对地表建筑的振动影响、隧洞围岩收敛变形、施工进度快慢等,采用正交试验和灰色关联度分析法对小净距隧道爆破施工进行优化设计,并结合组合赋权法最终确定一种既能提高隧道施工的安全性,又能兼顾工期的最优化施工方案。
1 工程概况
福州轨道交通2号线工程洋里站南端矿山法段两隧道全长均约72 m,两隧道净距仅1.6~3.5 m,属超小净距隧道,其中左洞为先行洞,右洞为后行洞,且两隧道的断面尺寸一致,断面最宽处距离均为7.2 m,隧道净空高度为8.4 m。两隧道爆破施工时相互影响程度较高。隧道覆土厚度约9.0~11.2 m,相对较浅,属于浅埋。围岩级别为Ⅵ~Ⅴ,施工难度极大。如何选取合理的步距和开挖进尺,既能控制地面振速和隧道稳定性,又能保证工期是施工单位急需解决的难题。图1为洋里站隧道进口。
2 数值模拟
2.1 模型尺寸及参数
根据福州地铁2号线洋里站南端矿山法段的实际情况建立三维模型。考虑到隧道对围岩扰动的影响范围为3~5倍的隧道洞径,因此取模型的,,方向的尺寸分别为48,72和30 m,其中方向上部中风化岩厚度为8 m,下部微风化岩厚度为22 m,模拟开挖方式为上下台阶开挖。左右洞隧道的尺寸相同,隧道断面最宽距离均为7.2 m,高度为8.4 m,其中上台阶高度为4.4 m,下台阶高度为4 m,两隧道之间的净距为1.6 m。且4个侧面和底部均设置为无反射的黏性边界[11]。图1为数值网格模型。

(a) 数值网格;(b) 隧道模型
根据施工现场提供的地勘报告可知,洋里站所处地层为复合地层,其上部地层为厚度8 m的中风化岩,下部地层为厚度22 m的微风化岩。具体岩层参数取值见表1。

表 1 岩层参数
2.2 爆破方案及荷载
在现场进行监测试验时,由于隧道净距较小,同时断面较小,因此现场初步方案一致采用上下台阶爆破开挖方式。此次现场爆破测试具体情况为:左右洞掌子面错开距离为10 m,上台阶爆破进尺为4 m,上台阶长度为12 m,分为7段,且上下台阶隔天起爆,其中每段爆孔个数以及爆孔装药量见表2。图2为现场上台阶炮孔布置图。

表2 上台阶爆破参数

单位:cm
在隧道掘进爆破过程中,一般是分布在一定空间内的多孔装药起爆,围岩内壁任意一处由爆破产生的应力是多个应力波叠加的结果,目前还没有一种理论方法能较为准确地计算多孔装药起爆在围岩内壁产生的应力。由于掏槽孔距离隧道轮廓面较远,对围岩的扰动较小,因此,本文主要考虑周边眼所产生的爆破荷载,即对应于上台阶中的15段,并认为爆破荷载均匀的作用在开挖面轮廓线各单元节点上,作用方向为洞周法线方向。周边眼装药量是根据周边眼炮孔的数目,炮孔的深度,装药的耦合度来确定的,本文中近似认为炮孔深度代表开挖进尺。由于现场多采用不耦合装药,根据文献[12]可知,在不耦合装药情况下,爆孔岩石壁受到爆破荷载时程函数为:

式中:ρ0为炸药密度;D为炸药炮轰速度;lc为炮孔长度;lb为装药长度;dc为炮孔直径;db为装药直径;b为阻尼系数;t为作用时间;n为爆轰产物撞击内壁时的压力增大倍数,取值多为8~11,这里取10。周边眼的具体装药结构如图3所示,其中lb=lb1+lb2+lb3+lb4+lb5+lb6+lb7。本文中,当作用时间t=tr=6 ms时,爆破荷载达到峰值P0,爆破荷载时程曲线如图4所示。
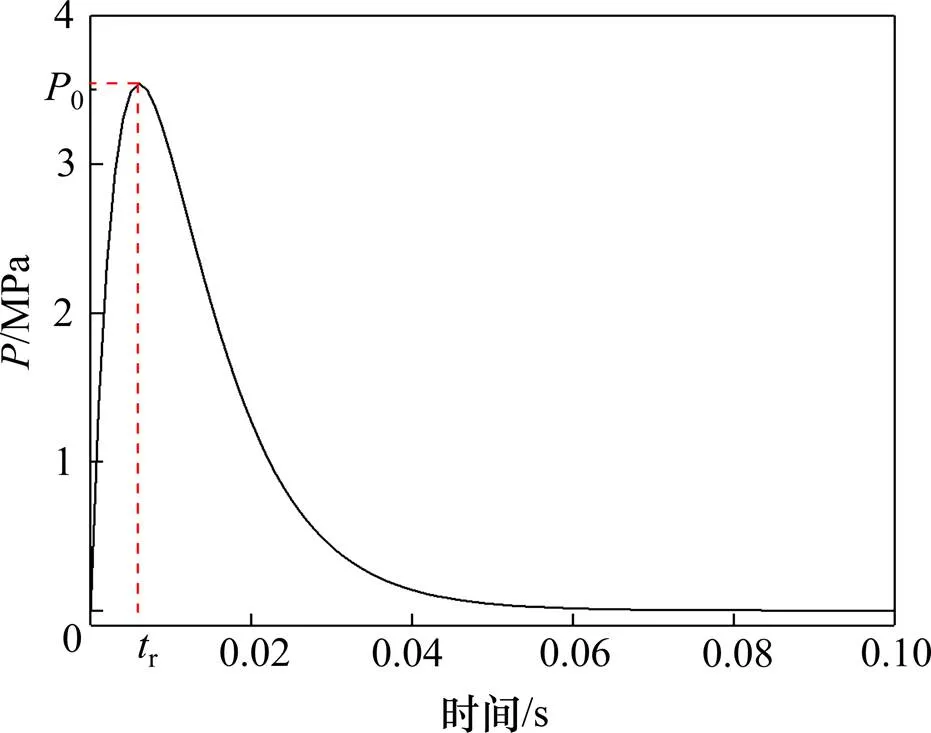
图4 爆破荷载时程曲线
2.3 结果对比分析


表3 现场采取方案计算结果

图5 现场实测振速曲线
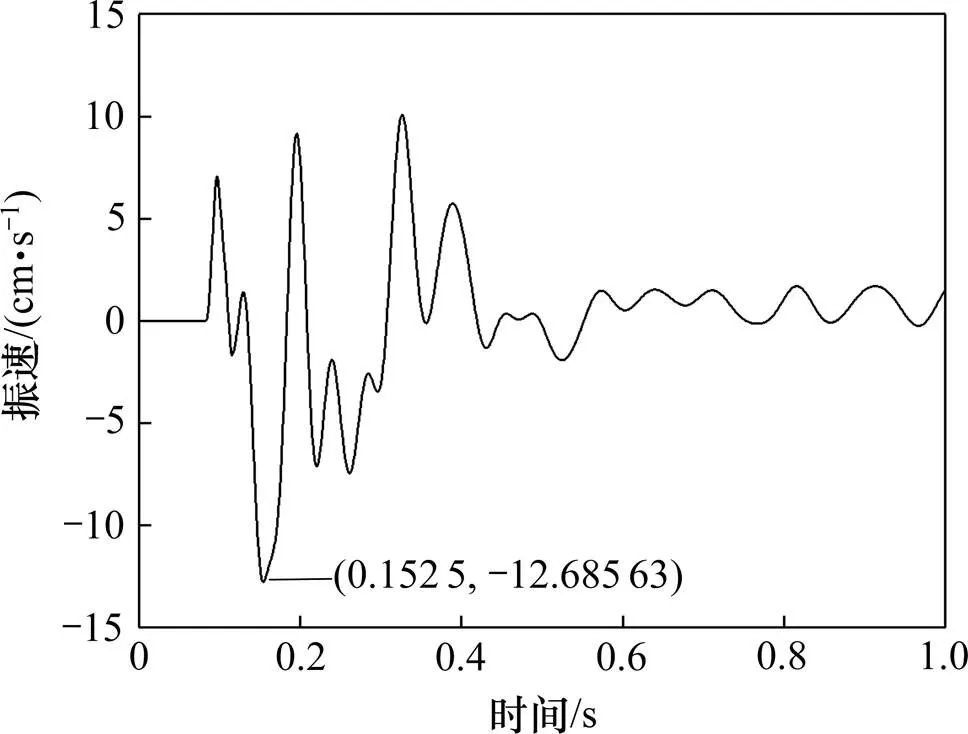
图6 模拟振速曲线
通过观察表3和图5和6可发现,数值模拟振速曲线频率低于实测振速曲线,主要源于模拟将爆破荷载简化了,但两者大体的趋势和峰值相差较小,说明数值计算用于分析小净距隧道爆破施工是具有可行性的。
3 正交试验设计
3.1 确定试验因素与评价指标
由隧道贯通总时长的计算公式()易知左右洞的开挖进尺和上台阶长度会对工期产生影响,另开挖进尺和左右洞的掌子面的错开距离会对地表振速、隧道内壁收敛变形以及中隔岩柱的应力产生影响。综合以上因素,将D,,和作为正交试验的评价指标。
3.2 正交试验设计过程
正交试验是以正交表为依据对试验进行整体设计、统计分析,从而可以实现进行少数试验便能找到最佳方案的一种方法。本文中将,和作为正交试验的因素,设计了如表4所示的三因素四水平的正交试验。根据参考文献[13]可知,一般上下台阶法施工中,只有当上台阶长度大于1~1.5倍洞宽,即上台阶长度至少为7.6 m时,上下断面基本上可以采用平行作业。以D,,和作为正交试验的评价指标作为小净距隧道爆破施工优化设计评价指标,具体正交试验设计见表4。表5为不同工况数值计算结果。

表4 正交试验设计

表5 数值计算结果
4 数据处理
4.1 灰色关联度
本文通过比较左右洞不同错开距离、不同开挖进尺、不同上台阶长度等参数与结果评价标准之间的灰色关联度,确定隧道爆破施工最优参数。计算灰色关联度的具体步骤如下。
4.1.1 构造指标矩阵
根据灰色关联分析法原理可假设评价系统是由个评价指标和个试验方案组成,本文中=4,=16,可构造评价指标矩阵如式(2)。

4.1.2 指标矩阵归一化处理
由于本文爆破施工优化系统中的各种评价指标均是越小越优,矩阵归一化处理后有:

式中:=1,2,…,;=1, 2,…,。
矩阵经过式(3)处理后:

4.1.3 计算关联系数矩阵


4.2 组合赋权法
权重赋值法主要分为主观赋权法和客观赋权法,其中常见的主观赋权法有:专家评分法和层次分析法;常见的客观赋权法有:粗糙集[15]、均方差法[16]、熵值法[17]等。为了使决策结果更加真实可信,本文结合熵值法和层次分析法确定评估指标的组合权重。
4.2.1 熵值法
对指标矩阵进行归一化处理:

各个指标的信息熵:
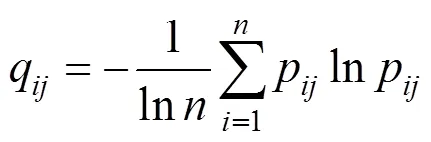
熵值法权重:

4.2.2 组合权重
将主观权重和客观权重进行组合处理,具体组合权重计算公式为:

式中:α为基于熵值法的客观权重;为基于层次分析法的主观权重;为综合权重。
4.2.3 最优化方案的关联度计算
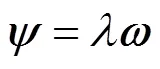
式中:为目标函数灰色关联度矩阵;为组合权重系数矩阵。
4.3 确定最优化参数组合
隧道爆破施工优化设计中的后行洞右侧拱腰水平位移、中隔岩有效应力、地表振速、双洞贯通时长数值均越小越好,根据式(1)~(6)计算得灰色关联系数矩阵为:

通过式(7)~(9)计算得到主、客观权重结果分别为=[0.153 8 0.076 9 0.615 4 0.153 8],α=[0.073 6 0.181 3 0.107 8 0.637 2];然后结合式(10)计算组合权重为:=[0.059 7 0.073 6 0.349 9 0.516 9];最后通过式(11)计算目标函数关联度见表6。4水平平均关联度见表7。图7为关联度柱状图。
通过分析表7和图8可知,小净距隧道爆破施工最佳施工方案为左右洞错开20 m,爆破开挖进尺选为3 m,上台阶长度选为10 m。

表6 目标函数关联度

表7 四水平平均关联度

图7 关联度柱状图
5 施工优化结果分析
通过观察表7中的数据可发现小净距隧道爆破施工优化设计参数的最佳组合为“左右洞错开距离为20 m,爆破开挖进尺为3 m,上台阶长度为10 m”。这一组组合数据并没有在正交试验表中出现,说明采用正交试验方法虽然减小了试验次数,但并不影响找到最佳参数组合。为了确定该组合是否为最佳参数组合,需要对该方案进行数值计算,计算结果见表8。

表8 优化前后各项指标数数值对比
通过分析表8可知,采用优化后的施工方案虽然在贯通时长上增加了13 d,但在工程建设的允许工期范围内,是可以被接受的;而后行洞右侧拱腰处的水平位移峰值降低了11.4%,中隔岩有效应力峰值降低了33.7%,地表振速峰值降低了12.84%,因此小净距隧道采用优化后的方案进行施工能够有效的控制中隔岩收敛变形值、有效应力值以及地表振速峰值。
6 结论
1) 运用正交试验和灰色关联度分析,并结合组合赋权方法,综合考虑主观和客观因素,实现进行较少试验次数便能获得最佳试验参数的目的,说明了正交试验−灰色关联度分析法具有较强的工程使用价值,值得推广。
2) 通过正交试验和灰色关联度分析,确定小净距隧道爆破施工最优方案为左右洞错开距离为20 m,爆破开挖进尺为3 m,上台阶长度为10 m。
3) 小净距隧道爆破施工优化后,后行洞右侧拱腰处水平位移峰值降低了11.4%,中隔岩有效应力峰值降低了33.7%,地表振速峰值降低了12.84%。隧道爆破施工的安全性达到了大幅的提升,施工优化效果明显。
[1] ZOU Xinkuan, ZHANG Jichun, PAN Qiang, et al. Simulated analysis of ground vibration characteristics caused by excavation blasting of shallow tunnels with small clearance[J]. Journal of Disaster Prevention and Mitigation Engineering. 2016, 36(4): 646−651.
[2] 凌同华, 曹峰, 张胜, 等. 分岔隧道过渡段的爆破振动特性研究[J]. 振动与冲击, 2018, 37(2): 43−50. LING Tonghua, CAO Feng, ZHANG Sheng, et al. Blasting vibration characteristics of transition section of bifurcated tunnel[J]. Vibration and Impact, 2018, 37(2): 43−50.
[3] Sterpi D, Cividini A. A physical and numerical investigation on the stability of shallow tunnels in strain softening media[J]. Rock Mechanics & Rock Engineering. 2004, 37(4): 277−298.
[4] 苏芳芮. 城市小净距公路隧道开挖方法的力学行为研究[D]. 重庆: 重庆交通大学, 2014. SU Fangrui. Mechanical behavior study on excavation method of urban small clear distance highway tunnel[D]. Chongqing: Chongqing Jiaotong University, 2014.
[5] 田明杰, 牟智恒, 仇文革. 基于BP神经网络的隧道稳定性分析研究[J]. 土木工程学报, 2017, 50(增2): 260− 266. TIAN Mingjie, MOU Zhiheng, QIU Wenge. Tunnel stability analysis based on BP neural network[J]. Journal of Civil Engineering, 2017, 50(Supppl 2): 260−266.
[6] 苑绍东, 杨林, 黄舰. 青岛地区地铁隧道爆破施工影响范围研究[J]. 现代隧道技术, 2018, 55(3): 76−80. YUAN Shaodong, YANG Lin, HUANG Jian. Study on the influencing range of metro tunnel blasting construction in Qingdao area[J]. Modern Tunnel Technology, 2018, 55(3): 76−80.
[7] Koopialipoor M, Jahed Armaghani D, Haghighi M, et al. A neuro-genetic predictive model to approximate overbreak induced by drilling and blasting operation in tunnels[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(2): 981−990.
[8] Hyun K, Min S, Choi H, et al. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels[J]. Tunnelling and Underground Space Technology, 2015(49): 121−129.
[9] Nezarat H, Sereshki F, Ataei M. Ranking of geological risks in mechanized tunneling by using fuzzy analytical hierarchy process (FAHP)[J]. Tunnelling and Underground Space Technology, 2015(50): 358−364.
[10] 陈育民, 徐鼎平. FLAC/FLAC3D基础与工程实例[M]. 北京: 中国水利水电出版社, 2009. CHEN Yumin, XU Dingping. FLAC/FLAC3Dfoundation and engineering examples[M]. Beijing: China Water Conservancy and Hydropower Press, 2009.
[11] 孙艳军, 赵亚克, 张世平. 新柳林河隧道掘进爆破对既有隧道的影响[J]. 爆破, 2015, 32(1): 75−80. SUN Yanjun, ZHAO Yake, ZHANG Shiping. Influence of excavation blasting of new Liulin river tunnel on existing tunnel[J]. Blasting, 2015, 32(1): 75−80.
[12] LI D Q, XIAO T, CAO Z J, et al. Auxiliary slope reliability analysis using limit equilibrium method and finite element method[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1004−1013.
[13] 邓聚龙. 灰色控制系统[J]. 华中工学院学报, 1982, 10(3): 9−18. DENG Julong. Grey control system[J]. Journal of Huazhong Institute of Technology, 1982, 10(3): 9−18.
[14] 王铁滨, 刘文龙. 基于粗糙集理论的光纤传感网络故障诊断系统[J]. 激光杂志, 2019, 40(3): 130−134. WANG Tiebin, LIU Wenlong. Fault diagnosis system of optical fiber sensor network based on rough set heory[J]. Laser Magazine, 2019, 40(3): 130−134.
[15] 孙佳美, 任秀丽. 无线传感网中基于均方差赋权法的路由协议[J]. 传感技术学报, 2019, 32(2): 258−265. SUN Jiamei, REN Xiuli. Routing protocol based on mean square error weighting in wireless sensor networks[J]. Journal of Sensing Technology, 2019, 32(2): 258−265.
[16] 林春荣, 杨晓英. 基于熵值法和序关系分析法的产品质量评估[J]. 组合机床与自动化加工技术, 2018(10): 156−160. LIN Chunrong, YANG Xiaoying. Product quality evaluation based on entropy method and rank correlation analysis[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2018(10): 156−160.
Optimization and analysis of blasting construction of shallow-buried tunnel with small clear spacing in city
WU Bo1, 2, LAN Yangbin1, 2, YANG Shisheng1, 2, WANG Shuaishuai3, DAI Yichang3
(1. College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China;2. The Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, Nanning 530004, China;3. China Communications First Highway Engineering Co., Ltd, Wuhan 430056, China)
In order to optimize the blasting construction of Yangli Station of Fuzhou Metro Line 2, numerical software was used to calculate the vibration response of tunnel under different working conditions. In addition, three factors and four levels of orthogonal test were designed by taking the staggered distance between left and right holes, the length of blasting excavation footage and the length of upper steps as test factors, and taking the peak horizontal displacement of backward hole, the peak effective stress of the middle rock, the peak surface vibration velocity and the length of the two holes as evaluation indexes. The grey relational degree analysis and combination weighting method were used to process the result data, and the optimal combination of parameters was obtained. The results show that the optimum blasting scheme for tunnel with small net distance is that the left and right holes are staggered 20 m, the blasting excavation footage is 3 m, and the length of the upper step is 10 m.Compared with the actual blasting scheme, the horizontal displacement of the middle diaphragm arch waist, the peak effective stress of the middle diaphragm and the peak surface vibration velocity of the tunnel are reduced by 11.4%, 33.7% and 12.84% respectively. The grey correlation analysis based on orthogonal experiment can obtain the optimal parameter scheme through a few times of experiments, which has a good application prospect.
small net distance; tunnel blasting; numerical simulation; orthogonal test; grey relational analysis
U455.6
A
1672 − 7029(2020)05 − 1201 − 08
10.19713/j.cnki.43−1423/u.T20190688
2019−07−31
国家自然科学基金面上资助项目(51478118,51678164);广西特聘专家专项资金资助项目(20161103);广西自然科学基金资助项目(2018GXNSFDA138009);广西科技计划资助项目(桂科AD18126011);广西大学科研基金资助项目(XTZ160590);广西岩土与地下工程创新团队资助项目(2016GXNSFGA380008)
吴波(1971−),男,四川阆中人,教授,博士,从事隧道及地下工程方向的教学与研究工作;E−mail:813792833@qq.com
(编辑 蒋学东)

