相依指数分布次序统计量的随机比较

张 帅，方龙祥

（安徽师范大学数学与统计学院，安徽芜湖241002）

在日常生活中，次序统计量被广泛运用在应用概率、生命实验、可靠性理论、统计推断等领域，是近些年来的研究热点。当观察样本是独立同分布时，次序统计量的研究已经非常广泛，但在许多现实情形中，观察样本通常是独立非同分布或者是既不独立也不同分布的。现有文献中，研究最多的是来自于指数分布的次序统计量。最早在文献[1]中被讨论，令X1,X2,…,Xn是一组独立指数随机变量，且Xi～E(λi)，i=1,2,…,n；令是另一组独立指数随机变量，且其证明了[1]

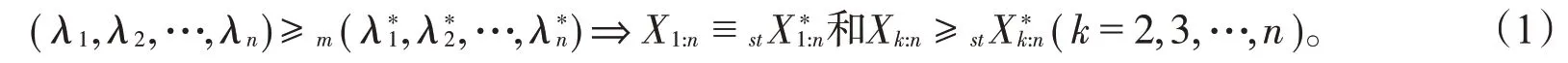
随后，Proschan等[2]将上述结果从普通随机序加强到普通多元随机序，紧接着Khaledi 等[3]将(1)式部分改进后，得出在p-larger 下对于其他结论可以参阅文献[4-5]等。

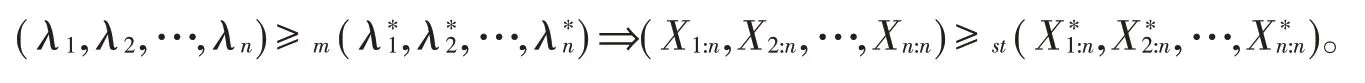
本文主要研究在非独立情形下的指数分布。为了刻画指数分布下随机变量的相关性，这里引入了Copula函数[6]，并使用阿基米德Copula工具[7-8]来刻画随机变量的相依性。

1 有关概念及性质

优化序是重排向量元素以后的一种偏序。

定 义 1[9]（1）令表 示 两 个n维 实 向 量 ，令分别为λ和λ*的分量由小到大的有序排列。若

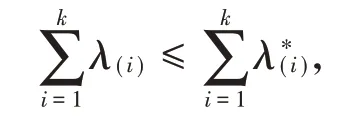
对所有的k=1,2,…,n-1成立，且那么称λ优化于λ*，记为λ≥mλ*。

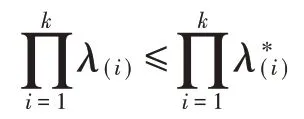
成立，则称在p-larger序下λ比λ*大，记为λ≥pλ*。

定义2[10]对定义在n维实数空间上的多元函数φ:ℝn→ℝ，如果对于所有其定义域内的向量x≥my满足：（1）φ(x)≥φ(y)，则称φ是Schur凸函数；（2）φ(x)≤φ(y)，则称φ是Schur凹函数。

下面的不等式通常用来判定Schur凸（凹）函数。若多元实值函数中的φ为置换对称函数且可导，则称φ为Schur凸（凹）函数的充要条件是对所有的i≠j满足如下不等式：

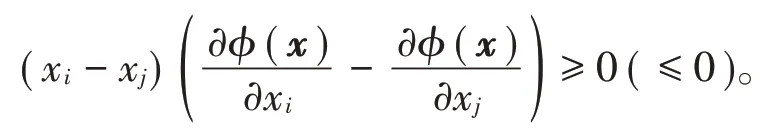
定义3[8]阿基米德Copula是Copula函数的一种，其表达式为

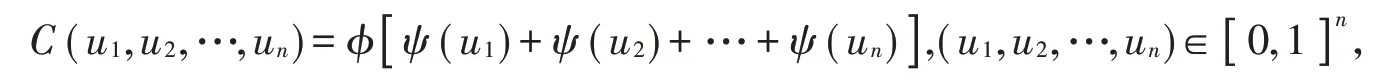
其中，φ(u)称为阿基米德Copula函数C(u1,u2,…,un)的生成元，满足以下性质：

（2）(-1)kφk(x)≥ 0，k=0,1,…,n-2；

（3）ψ=φ-1。

阿基米德Copula 函数的生成元φ(u)决定了其函数表达式。下面以阿基米德Copula 中Frank 连接函数为例其形式为

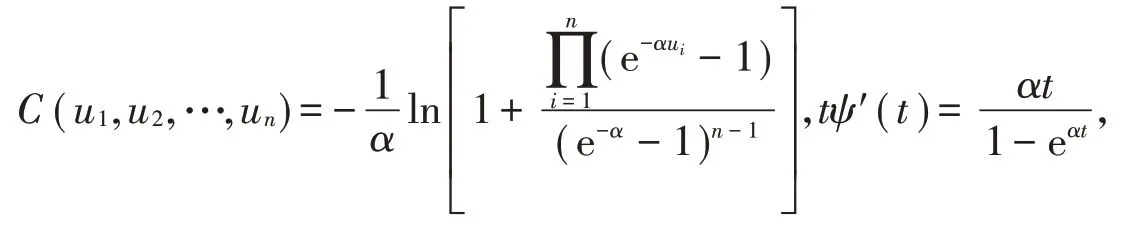
当α＞ 0时，tψ′(t)是关于t单调递增的函数；当α＜ 0时，tψ′(t)是关于t单调递减的函数。

注1当生成元φ(t)=e-t，ψ为φ反函数，则此时为独立情形。

定义4[11]（1）设X和Y是两个随机变量，若对任意的t∈ ℝ，都有P(X＞t)≤P(Y＞t)成立，则称随机变量X在普通随机序的意义下小于Y，记为Y≥stX。

（2）设X=(X1,X2,…,Xn) 和Y=(Y1,Y2,…,Yn) 是两个随机向量，若对任意的单调增加函数f(x1,x2,…,xn)(每个分量是增加的)有f(Y)≥st f(X)，则称随机向量X在普通多元随机序下小于Y，记为Y≥stX。

2 主要结论

定理1令X1,X2,…,Xn是一组随机变量，且Xi～E(λi)，i=1,2,…,n，其相依性由生成元为φ(t)的阿基米德Copula刻画；令是另一组随机变量，且其相依性由生成元为φ(t)的阿基米德Copula刻画。若则。

证明当只要证明对于x＞ 0，

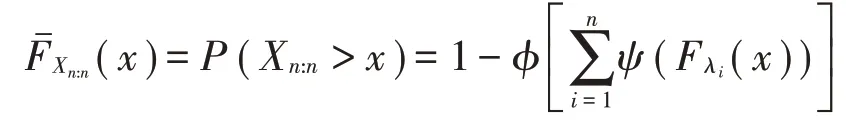
关于(λ1,λ2,…,λn)是Schur凸函数即可。

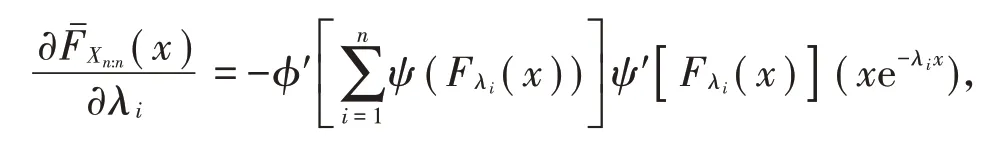
故可得，

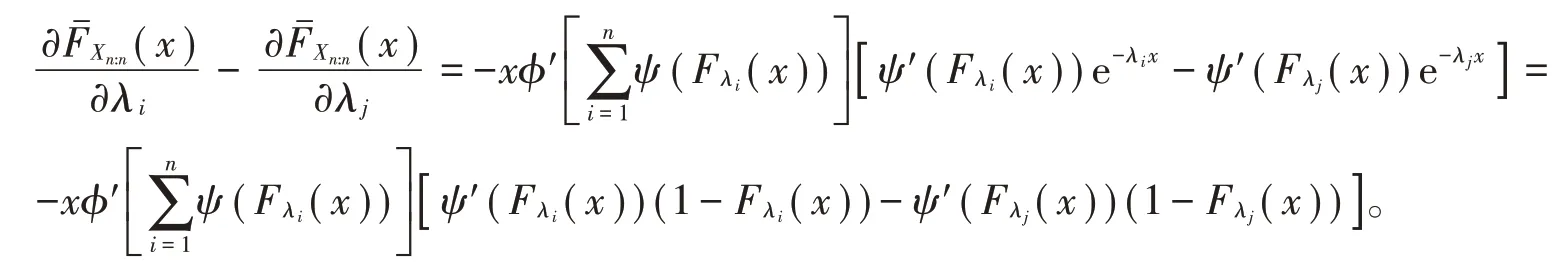
由于φ′≤ 0，则

令h(t)=ψ′(t)(1-t)，h′(t)=ψ″(t)(1-t)-ψ′(t)。因ψ′(t)≤ 0，ψ″(t)≥ 0，t∈ [ 0 ,1 ]，h′(t)≥ 0，故h(t)是一个单调递增的函数。当λi≥λj时，Fλi(x)是随着λi的增大而增大，ti=Fλi(x)，i=1,2,…,n，ti∈[ 0 ,1 ]，则

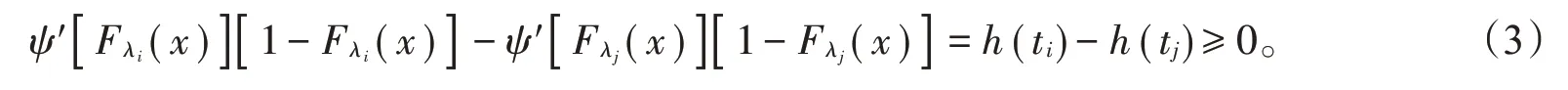
由（2）式和（3）式，可得：

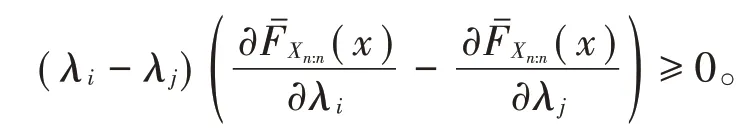
例 1令X1,X2,X3是一组随机变量，且Xi～E(λi)，i=1,2,3，对应参数向量λ=(0.6,0.2,0.2)；令是另一组随机变量，且，对应参数向量λ*=(0.4,0.3,0.3)，都有一样的Frank Copula和生成元当α=5时如图1所示；同样，当α=-5，有如图2所示。由两图的图像可以看出与定理1结论一致。

定理2令X1,X2,…,Xn是一组随机变量，且Xi～E(λi)，i=1,2,…,n，其相依性由生成元为φ(t)的阿基米德Copula 刻画；令是另一组随机变量其相依性由生成元为φ(t)的阿基米德Copula刻画，

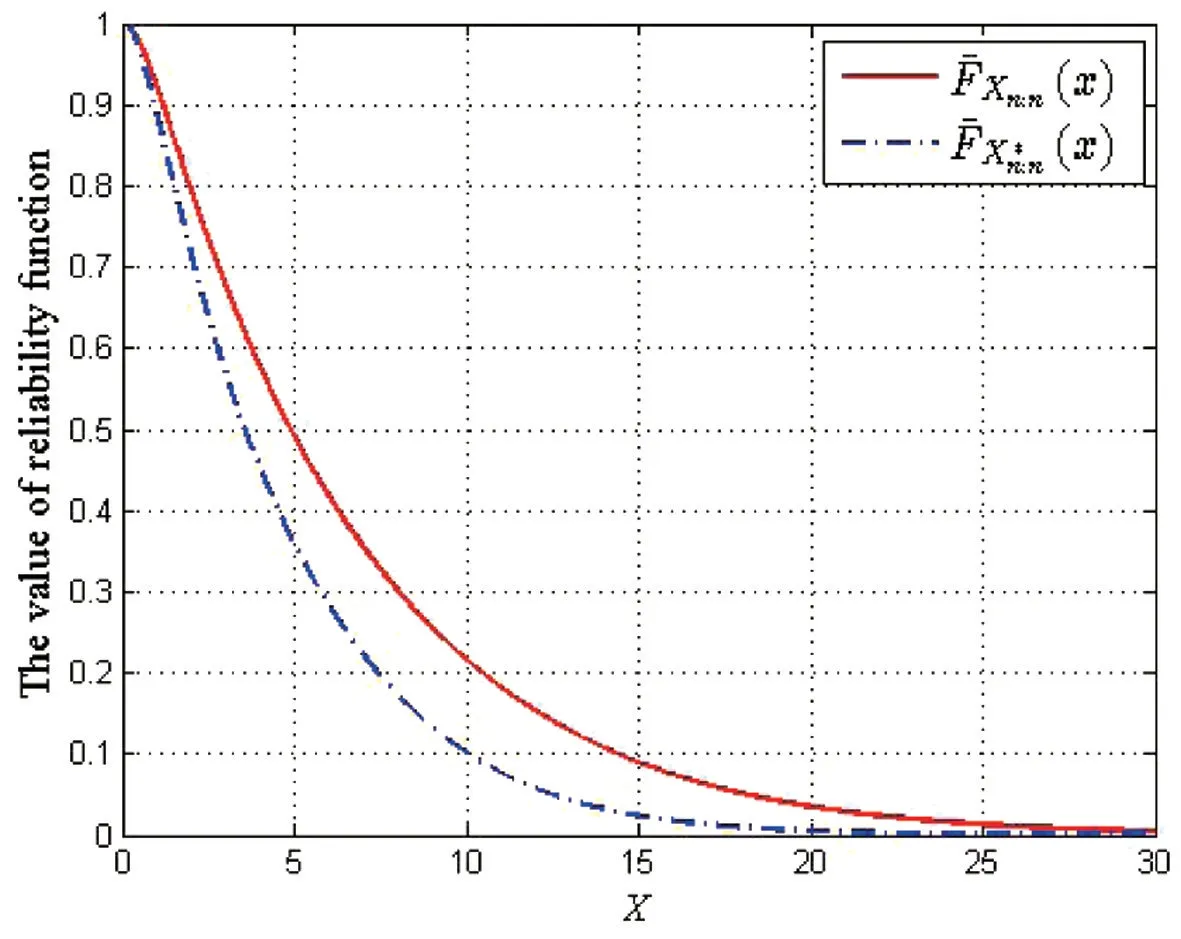
图1 α=5时(x)与(x)的图像

证 明（1）当且关于t单调递增，若证只要证明对于关于(λ1,λ2,…,λn)是Schur凹函数即可。

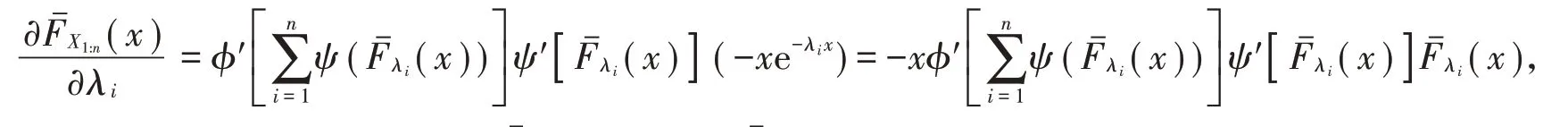
由于φ′≤ 0，则

若tψ′(t)关于t单调递增，则λi≥λj时，

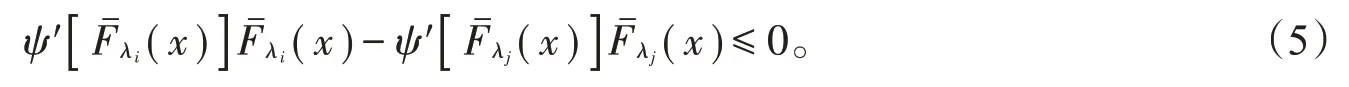
由（4）式和（5）式，可得：

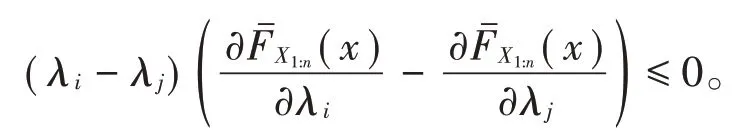
类似的，若tψ′(t)关于t单调递减，则λi≥λj时

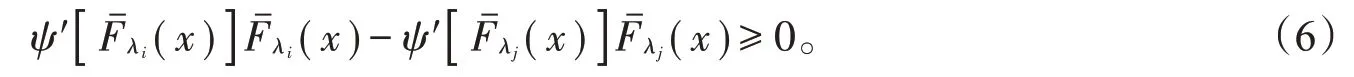
由（4）和（6）式，可得：

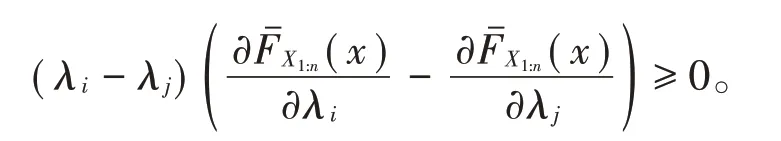
因此，FˉX1:n(x)是关于(λ1,λ2,…,λn)的Schur凸函数，于是由定义2和定义4得。

注2当φ(t)=e-t时既是关于t单调递增的函数，也是关于t单调递减函数，从而由定理2得同时成立，也即此结论与文献[1]中研究来自于独立指数分布的次序统计量的结论一致。

例 2令X1,X2,X3是一组随机变量，且Xi～E(λi)，i=1,2,3，对应参数向量λ=(0.6,0.2,0.2)；令是另一组随机变量，且对应参数向量λ*=(0.4,0.3,0.3)，都有一样的Frank Copula和生成元当α=5时，tψ′(t)是关于t单调递增的如图3所示，当α=-5，tψ′(t)是关于t单调递减的，如图4所示。由两图的图像可以看出与定理2结论一致。

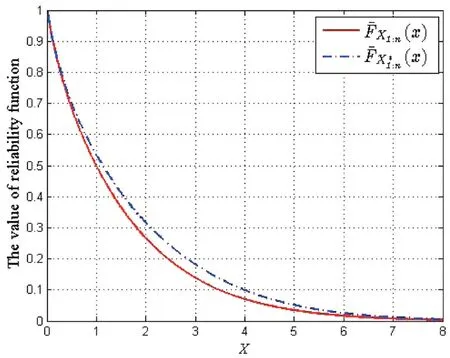
图3 α=5时，(x)与(x)的图像

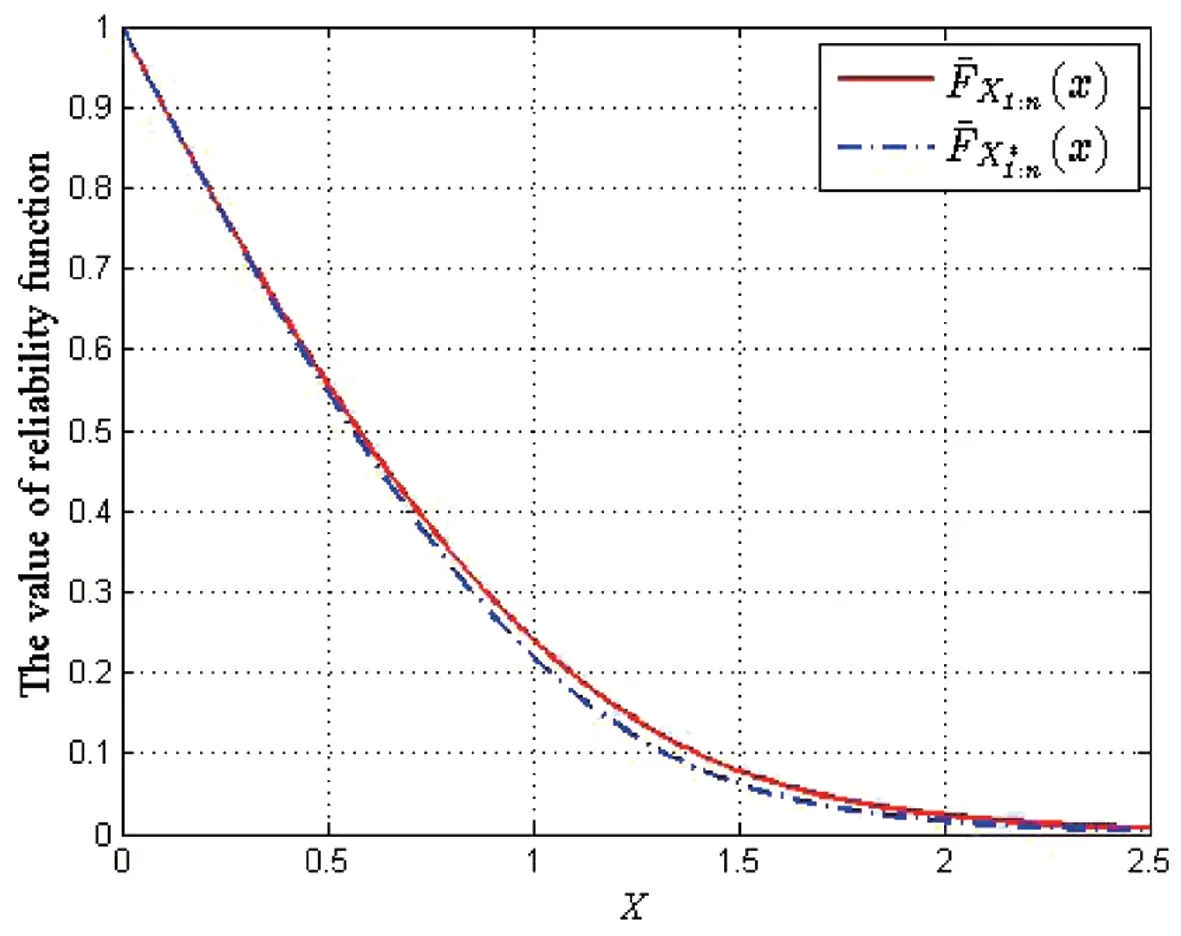
图4 α=-5，(x)与(x)的图像

3 总 结

本文主要讨论了相依指数分布下最大与最小次序统计量的随机比较，具体地说就是通过优化序这个工具，找到了指数分布中参数满足的条件，同时，运用阿基米德Copula刻画指数随机变量之间的相关性，最后，研究了由n个不独立且不同分布的指数随机向量的最大与最小次序统计量在普通随机序下的随机比较。但是，本文仅给出了相依指数分布下最大与最小次序统计量的随机比较，对于其它阶次序统计量Xi:n(i=2,3,…,n-1)的随机比较，仍然是个挑战。