基于改进UKF的组合导航系统航向角估计方法研究

程建华，王 诺，尚修能

(哈尔滨工程大学自动化学院，哈尔滨 150001)

0 引言

捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)与全球卫星导航系统(Global Navigation Satellite System，GNSS)在误差传播性能上互补，组合之后的系统精度、性能和可靠性等多个方面均优于单独的子系统，具有良好的应用前景[1]。SINS/GNSS通常用于陆地车辆导航，为其提供可靠的速度、位置和姿态信息。伴随着微机电系统(Micro-Electro-Mechanical System，MEMS)技术的快速发展，基于MEMS技术的惯性器件因具有低成本、低功耗、小体积以及可大批量生产等优势[2]，受到了广泛关注。但由于成本的降低导致MEMS陀螺仪的输出存在许多不确定性误差，使得陀螺仪的姿态精度降低，从而导致整个导航系统的精度下降[3]。因此，必须提出一种能够提高MEMS-SINS/GNSS组合导航系统姿态估计精度的解决方案。

采用速度、位置和姿态全组合方式进行组合导航，虽然相较于传统的位置和速度组合方式的姿态角精度有了较大改善，但在实际应用中实现复杂，抗干扰性差，且只适用于多天线卫星导航系统[4-5]。文献[1]在简化组合导航模型的基础上进行姿态估计，使用常规组合导航的算法解算横摇角与纵摇角，对于航向角则采用级联卡尔曼滤波算法进行单独估计。这种方法虽然能够得到精度较高的姿态角，但是系统运算量增大，从而导致其实时性变差[6]。而文献[7]则研究了线性系统下，基于改进常规卡尔曼滤波的姿态估计算法，但是该算法并不能直接应用于非线性系统中[8]。因此，目前需要一种针对非线性系统的导航估计算法，在提高导航精度的同时减少计算量，提升系统的实时性。

针对上述问题，本文建立了以速度、位置和航向角误差为系统状态矢量的组合导航模型。首先对传统的速度和位置组合导航非线性系统进行可观测性分析，为了增强航向角的可观测性、抑制航向角易发散的问题，辅助以GNSS航向角作量测量；采用转弯判断规则和自适应算法降低了GNSS测量误差对姿态估计的影响。上述方法具有良好的适应性，导航精度高、实时性强，满足运载体的导航需求。

1 SINS/GNSS非线性误差模型

由于捷联惯导系统的误差模型本质上为非线性的，并受限于惯性器件本身的测量误差等因素，使得系统显示出较强的非线性和时变性。直接建立非线性误差模型，能够减少约束条件，使得误差模型能够更准确地描述系统的误差传播特性，有助于分析并提高系统的导航性能。

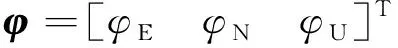
(1)

式中，各项变量定义见文献[6]。

由误差方程建立滤波状态微分方程为[11]

(2)

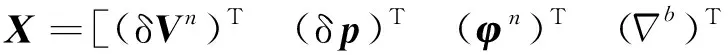
由于陆地车辆导航不需要考虑天向位置和速度，所以量测方程为

(3)

式中

(4)

其中，Z(t)是l×1观测向量；ZV和ZP分别由SINS和GNSS的速度和位置的差值得出；V为零均值噪声向量[12]。离散化状态方程和量测方程之后，对SINS/GNSS进行积分，获得长时精度的位置和速度。系统原理如图1所示。

图1 MEMS-SINS/GNSS系统原理Fig.1 System principle of MEMS-SINS/GNSS

2 非线性系统可观测性分析

对系统进行可观测性分析能够确定卡尔曼滤波效果的好坏，系统状态的可观测性可以反映该状态的估计精度，并确定收敛速度的快慢[13]。对于不可观测的状态，系统无法精确估计甚至不能估计。可观测性分析中的定性分析为确定状态是否可观测，定量分析为确定状态的可观测程度，即可观测度[14]。通常，对于线性时变系统采用由Goshen-Meskin和Bar-Itzhack提出的分段线性定常系统(Piece Wise Constant System，PWCS)可观测性分析方法，即PWCS方法[15]。可观测度分析通常采用基于PWCS的奇异值分解(Singular Value Decomposition，SVD)方法，即SVD方法[16]。但是目前所有线性系统的可测性分析方法都无法直接应用于非线性系统，并且非线性系统的可观测性分析现在没有统一的定义方法。由于现有的非线性系统的分析方法实现复杂，难于应用，因此通过将非线性系统线性化为线性系统，然后使用PWCS方法和SVD方法对其进行可观测性和可观测度分析。

2.1 可观测性分析

对式(2)状态微分方程中的t在[tk,tk+1]上积分得

(5)

(6)

将f(X(t))在Xk处进行Taylor展开得

≜f(Xk)+F(Xk)(X(t)-Xk)

(7)

将X(t)在tk处进行Taylor展开得

(8)

将式(8)代入式(7)得

f(X(t))=f(Xk)+F(Xk)f(Xk)(t-tk)

(9)

将式(9)代入式(6)并积分得

(10)

式中，T=tk+1-tk。此即为得到的离散线性化状态方程。

(11)

所以，可以得出

(12)

对式(3)量测方程直接进行离散化得

Zk+1=HXk+1+Vk+1

(13)

结合式(13)得到

(14)

所有时间段i=1,2,…,j的总观测矩阵(Total Observability Matrix, TOM)构造如下

(15)

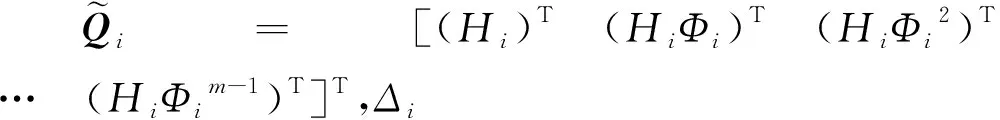
(16)

2.2 SVD可观测度分析

(17)

式中

(18)

(19)

其中，X(0)是初始状态矢量，经过矩阵变换可得

(20)

其中，Xi(0)是奇异值σi的初始状态矢量。所以第k个状态的可观测度定义为

(21)

其中，σi是使Xi(0)取得最大值的奇异值，σ0为观测量对应的奇异值。表1给出了在不同的外部观测量条件下的非线性系统可观测度分析结果。

表1 不同外部观测量条件下的系统可观测度

分析表1可知，增加外部观测量有效地提高了系统状态量的可观测程度。

3 航向角精确估计

3.1 GNSS航向角约束

速度位置组合导航系统通过常规无迹卡尔曼滤波器(Unscented Kalman Filter，UKF)滤波后可得到精度较高的俯仰角和横滚角。但是由于航向角可观测性弱，当载体为匀速直线行驶或者静止状态时，航向角误差较大，即使是在机动情况下，航向角的估计误差也不容忽略。所以，可通过增加航向角观测约束，提高航向角的可观测性和姿态角的精度。

单天线GNSS在多数情况下都可以给出速度、位置和航迹角。单天线GNSS航迹角为

(22)

式中，vE和vN分别为地理坐标系下单天线GNSS测得的东向和北向速度。在量测方程中加入航向约束，此时，量测量变为

(23)

式中，Zk为k时刻的量测向量；ΔVk、Δpk分别为k时刻MEMS传感器积分得到的速度、位置信息和GNSS获取的速度、位置信息的差值；Δφk为单天线GNSS航迹角与MEMS陀螺仪航向角的差值。

通过加入单天线GNSS航向约束可以解决航向角可观测性弱的问题，提高估计精度。

3.2 改进型滤波器

当运载体处于直线运动状态时，GNSS得到的航迹角与运载体的航向角是一致的，不存在偏流角的影响；但是当运载体处于转弯状态时，由于偏流角的存在，导致测量得到的航迹角与真实的航向角之间存在误差。由于系统先天存在这种误差，所以运载体在测量到转弯状态后，需要关闭GNSS航向辅助，短时间内仅通过陀螺积分来维持航向角的输出。但是由于MEMS-IMU的精度低，即使是短时间内关闭GNSS航向辅助也可能造成比较大的航向误差。为解决这个问题，对UKF进行了改进，从而有效地抑制了由于MEMS精度低而导致的航向误差增大。

3.2.1 转弯判断规则

通过单天线GNSS航向约束改善了航向角可观测性弱的问题，但是在载体转弯时会产生偏流角，GNSS测得的载体航迹角实际上为真实的航向角与偏流角之和，使得测量值与实际值之间产生了偏差。为了消除偏流角对系统的影响，在检测到车辆转弯时，关闭航向角观测。对于车辆转弯的判断可以通过测量转弯角速率的航向角陀螺的输出值导出，即

(24)

3.2.2 自适应UKF

常规UKF算法见文献[6]。对于系统中未知的噪声，利用基于Sage-Husa的极大后验估值算法对Qk和Rk进行估计。

(25)

(26)

结合UKF中的Pk/k-1则式(26)为

(27)

(28)

(29)

在这个基础上再采用渐消指数加权的方法，推导出非线性系统时变噪声统计估计器为

(30)

式中，dk=(1-b)/(1-bk)，b为遗忘因子，0

3.2.3 改进模糊自适应UKF

Sage-Husa滤波器通常会出现滤波发散的问题，为了解决这个问题，考虑在协方差匹配方法的基础上引入对滤波发散趋势的判断规则，即

(31)

其中，α为一可调的储备系数(α≥1)，依据实际情况进行设定；tr()为矩阵的迹。当式(31)成立时，表示滤波效果稳定;当该式不成立时，就需要对Pk/k-1进行修正，使其变为

(32)

其中，λk如下所示

(33)

其中，λ0为模糊UKF的残差理论值与实际值之间的比值。

模糊UKF的残差方差理论值为

(34)

实际残差方差为

(35)

所以，λ0为

(36)

由此，通过自适应加权系数λk对Pk/k-1的修正，来抑制滤波的发散情况。

4 仿真验证

为验证本文所提出的算法的有效性，进行了车载实验仿真验证，设置初始地理位置为北纬45°、东经126°，陀螺漂移误差为20(°)/h，加速度计零偏5×10-3g，GNSS的速度测量误差为0.01m/s，位置测量误差为10m，MEMS-SINS解算频率为100Hz，系统滤波频率为1Hz，仿真时长为3h，运行轨迹包括静止、匀速直线、加速、减速和转弯等状态。匀速直线运动时，北向速度为3m/s；加速运动状态时，北向加速度为2m/s2；减速时，北向加速度为-2m/s2；转弯状态时，航向角速率为-30(°)/s，转弯时长为3s，GNSS航向角量测存在偏流角。结果如下所示，图2～图4分别为常规UKF在匀速直线状态下的姿态、速度和位置误差曲线图；图5～图7分别为加入航向约束并在330s加入转弯状态的UKF算法与加入航向约束后改进UKF所得误差曲线的对比图。

图2 UKF姿态误差曲线图Fig.2 UKF attitude error curve

图3 UKF速度误差曲线图Fig.3 UKF speed error curve

图4 UKF位置误差曲线图Fig.4 UKF position error curve

图5 航向约束UKF和改进UKF姿态误差曲线图Fig.5 Course constraint UKF and improved UKF attitude error curve

图6 航向约束UKF和改进UKF速度误差曲线图Fig.6 Course constraint UKF and improved UKF speed error curve

图7 航向约束UKF和改进UKF位置误差曲线图Fig.7 Course constraint UKF and improved UKF position error curve

分析上述仿真结果，由图2可以看出，在无航向辅助常规UKF算法中，匀速直线状态下，由于航向角可观测性弱，UKF之后航向角误差与理想误差值之间始终存在差值，且无法通过改变初始值的取值而改善滤波的估值。由图5～图7可知，在加入航向角约束辅助后的直线行驶阶段，同无辅助姿态估计算法相比，航向角能够较好的收敛，但是幅值振荡较大，且在转弯状态下，姿态角出现了不同程度的发散，这是由于GNSS航向角在转弯时出现的偏流角等其他因素导致的量测误差较大引起的。所以，为了能够使转弯时得到更好的估算效果，则需要改进滤波算法，通过引入转弯判断规则和改进自适应UKF来增强算法的适应性，提高估计精度。由图5可以看出，姿态角的估计精度得到明显的提升，水平姿态误差控制在0.01°以内，航向角误差控制在0.1°以内，速度误差控制在0.02m/s以内，位置误差控制在1m以内。由此可以证明，该算法能够很好地完成运载体的长航时、高精度的导航需求。

5 结论

本文针对系统可观测性弱导致的姿态估计差等问题，提出了一种基于MEMS的非线性组合导航系统航向角估计算法。算法分析与实验结果证明：

1)通过采用单天线GNSS航迹角对系统进行航向约束的方法，解决了因航向角可观测性弱引起的姿态估计精度差的问题，实现了姿态角高精度估计。

2)通过采用转弯判断规则判断车辆是否处于转弯状态，并在检测到转弯状态后采用改进的Sage-Husa自适应无迹卡尔曼滤波器，解决了由于转弯时GNSS航向角量测存在偏流角而影响姿态估计精度的问题，从而得到了较好的估计效果。

3)通过仿真实验结果可以证明，本文提出的基于单天线GNSS的非线性系统航向角估计方法满足了低成本导航系统高可靠性和高精度的要求，具有重要的工程应用价值。