基于化学计量学的一次性塑料餐盒红外光谱分析

马 枭， 姜 红*， 杨佳琦， 刘轩侨

(中国人民公安大学刑事科学技术学院，北京100038)

近年来，一次性餐盒以其方便、快捷、成本低等特点被广泛应用于食品行业中。市面上在售的一次性塑料餐盒主要有聚丙烯、聚对苯二甲酸乙二醇酯和聚苯乙烯三类[1]。目前，常见的检验塑料制品的方法有红外光谱法[2]、拉曼光谱法[3]、扫描电镜/能谱法[4]、裂解气相色谱法和热分析法等，尚未见检验一次性塑料餐盒的报道。红外光谱法作为一种无损、快速的检验方法，在检验塑料制品领域得到了广泛应用。傅里叶变换红外(FTIR)光谱法凭借其无损检测、简便快捷且灵敏度较高的特点被广泛应用于微量物证检验之中[5]。传统方法主要是将样本谱图与标准谱图库进行比对分析得出结果，标准谱图比对仅能提供餐盒主要成分的信息，且该方法可能忽视样本之间细微的差异。例如，增塑剂、稳定剂、润滑剂等填料的红外光谱信息可能被遗漏，导致分类不准确[6]。因此，引入化学计量学对红外光谱数据进行分析，可以避免遗漏光谱中所含的主要、次要信息，提高分析效率与分析准确率。

化学计量学是一门运用数学、统计学、计算机科学以及其他相关学科的理论与方法，对化学测量数据进行处理，从中最大限度地获取有价值的化学信息的基础理论与方法学[7]。在处理样品原始红外光谱方面，可利用平滑降噪、散射校正、降维处理等化学计量学方法对原始数据进行处理。通过平滑的方式可去除干扰光谱信息的随机误差即噪声；通过散射校正可提高具有价值的信息在光谱中所占的比例；通过降维处理可简化分析过程，直观表述分析结果。本实验以样本红外光谱数据为基础，建立基于余弦相似度[8]、主成分分析和Fisher判别分析的分析方法，从向量、降维和函数三个角度出发，多方面考察样本之间的关联性，达到对一次性塑料餐盒准确分类的目的。

1 实验

1.1 谱图采集

本实验搜集了来自不同餐饮行业的35个一次性塑料餐盒样本(样品表略)，利用Nicolet-6700型傅里叶变换红外光谱仪(美国，Thermo Fisher)对样本进行谱图采集：扫描分辨率为4 cm-1，扫描次数设置为32次，扫描600～4 000 cm-1波段。以空气为背景进行采集，采集后扣除大气背景谱图，获得样品原始红外光谱图。

1.2 谱图预处理

利用光谱处理软件对所得的原始谱图进行基线校正处理，采用Savitzky-Golay法对谱图进行平滑处理：同时考虑平滑效果和特征丢失情况，选择多项式阶(Polynomial Order)为5，窗口点数(Points of Window)为60。利用多元散射校正(Multiplicative Scatter Correction)对所得谱图进行处理，达到提高原光谱信噪比的目的[9]。

2 理论基础

2.1 余弦相似度

余弦相似度(Cosine Similarity)是基于向量之间夹角的余弦值考察两向量相似度的一种方法。光谱相似度是表示各光谱之间的相似程度的一个量化值,对光谱分类等处理具有指导意义。除了对夹角余弦值进行计算外，还可以通过计算相关系数、欧氏距离、马氏距离等方法计算相似度[10]。在选定共有模式目标即对照谱图后，通过计算各样本谱图与其夹角余弦值，可计算出相对相似值，其计算公式如下：

(1)

其中，A和B是两个相互独立的测量向量，Ai是向量A的分量，Bi是向量B的分量。

2.2 主成分分析

主成分分析(PCA)是将多指标化为少数综合指标的一种统计分析方法[11]。在光谱多元统计分析中，往往存在着变量数目过多的情况。利用PCA提取其主成分，借助较少的综合变量解释代替较多的初始变量，在保证原信息损失较小的情况下同时降低数据维度[12]。主成分计算公式如下[13]：

(2)

其中，PC1,PC2,…,PCp是提取出的主成分；a1,a2,…,ap是确定的函数系数；X=(X1,X2,…,Xp)是一个p维的随机向量。

2.3 Fisher判别分析

Fisher判别分析基本思想是将m组n元数据投影到一个方向，使组内差异最小化，组间差异最大化，达到判别分类的目的[14]。判别分析不同于相似度的相似思想和主成分的降维思想，而是根据已知变量信息，不断拟合修正判别函数中的待定系数，最终形成判别函数，从而对新的样本进行分类。

3 结果与分析

3.1 相似度分析

随机选取12#样本作为共有模式样本，分别计算其余样本与之的相似度系数，相似度计算分布结果见图1。

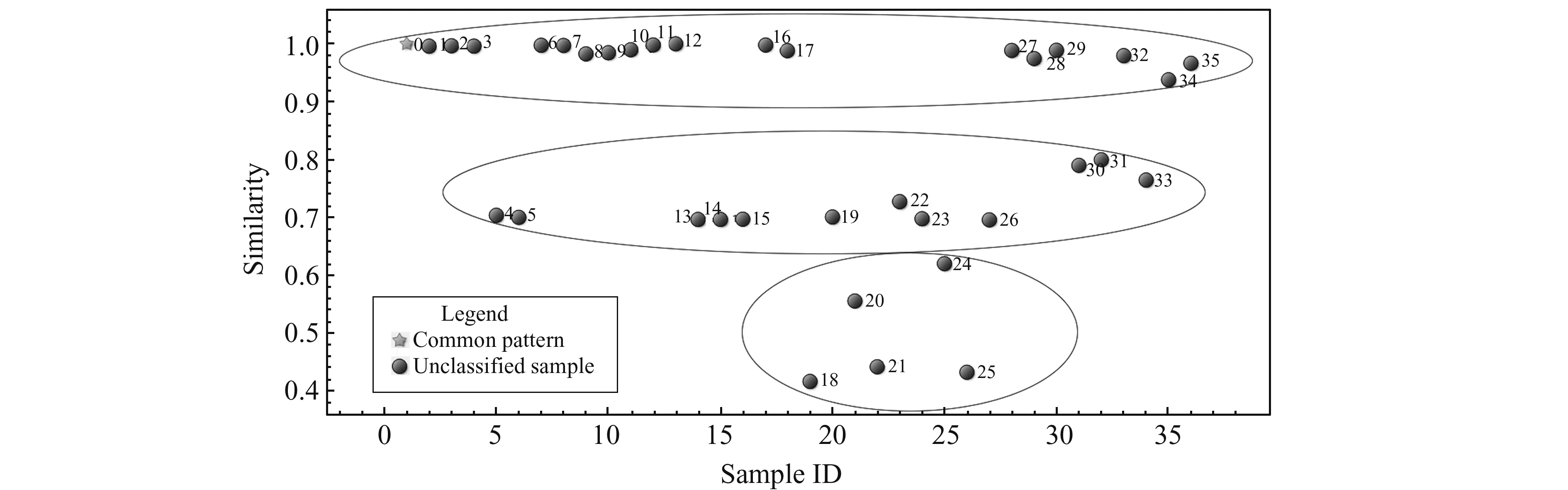
图1 35个样本相似度分析结果Fig.1 The results of similarity analysis of 36 samples

由图1可知，以12#样本作为共有模式样本进行相似度分析，35个样本根据其相似度值大致被分为了3类：相似度为0.4～0.7的样本有5个；相似度为0.7～0.9的样本有12个；相似度为0.9～1.0的样本有18个。三类样本的相似度差异较大，为后续分析分类提供了现实基础。

3.2 主成分分析

利用主成分分析对35个一次性塑料餐盒样本提取主成分，在累计方差大于85%的基础上，综合考虑各主成分的贡献率，最终选取累计贡献率最大的3个主成分，各主成分累计方差解释率见表1。

表1 累计解释方差贡献率

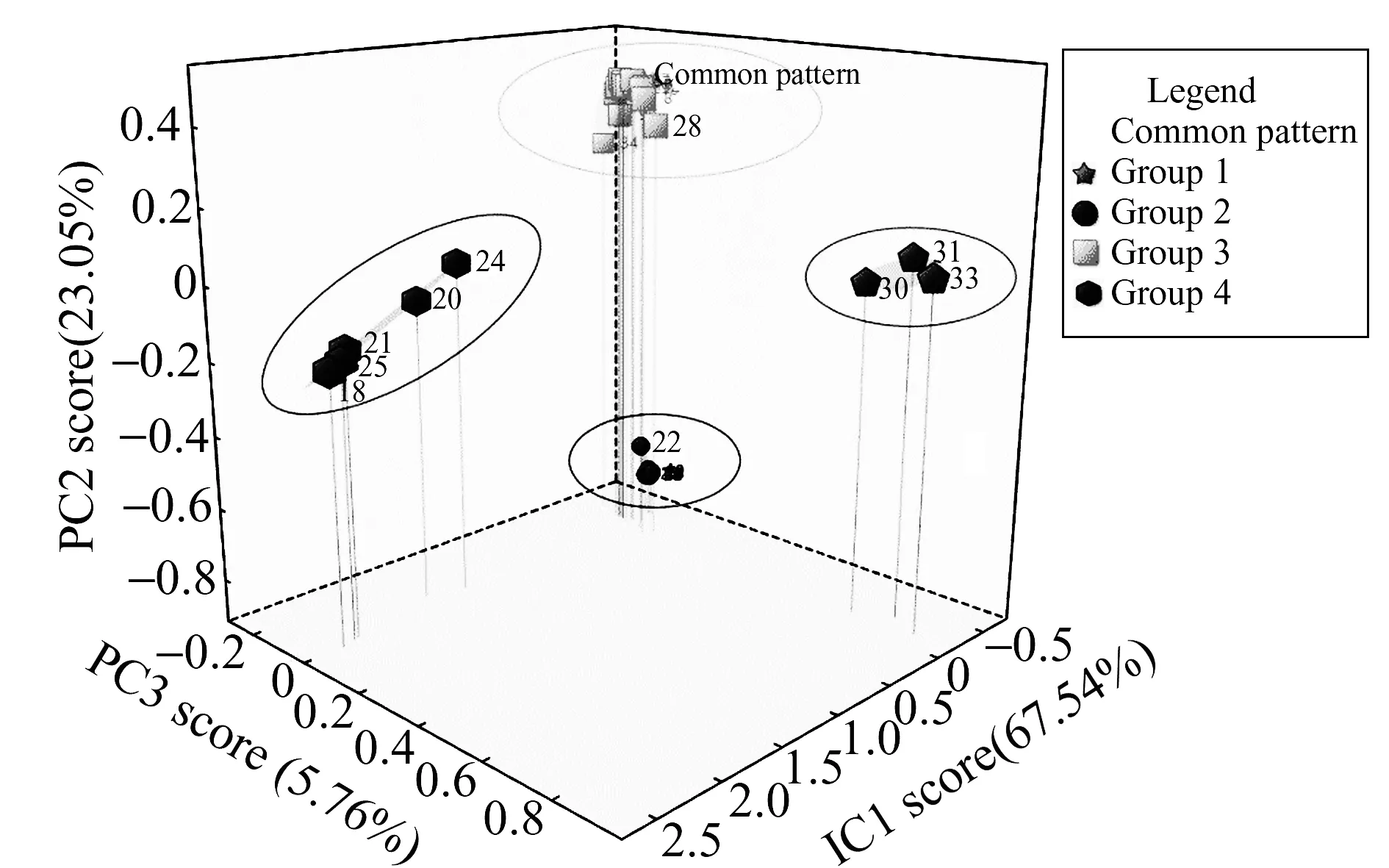
图2 35个样本主成分得分图Fig.2 The principal component score chart of 35 samples

分别计算35个样本的在各主成分上的得分，即各变量对于PC1、PC2、PC3三个主成分的重要程度，并绘制主成分得分图(图2)。35个一次性塑料餐盒样本根据其在不同主成分上的得分，被明显地分为了4类，且组内距离较小，组间距离较大，各组在三维空间上分散开来。主成分分析分类结果与相似度分析所分3类的结果不符，为探究其具体原因，对两种方法分类存在差异的样本：14#、19#、26#、30#、31#、33#进行相关性计算，考察其分类结果的准确性。

由表2可知14#、19#、26#三个样本之间相关性均大于0.99，表现出了极强的相关性，30#、31#、33#三个样本之间相关性均大于0.65，表现出了较强的相关性。但前三个样本与后三个样本之间相关性在0.25附近波动，相关性较弱，应分为两类。由此探究相似度分析分类结果错误原因：相似度分析是从向量角度入手，谱图数据可视为一个向量矩阵，数据维度较多且复杂，不同维度所求得相似度不同，最终相似度结果将各维度相似度结果叠加求和，并未考虑到各维度相似度的权重比，因此出现错误分类，但相似度分析仍是对未知类别样本进行初步分类的较好方法之一。因此在本实验中应当将35个一次性塑料餐盒样本按照主成分分析结果分为4类。

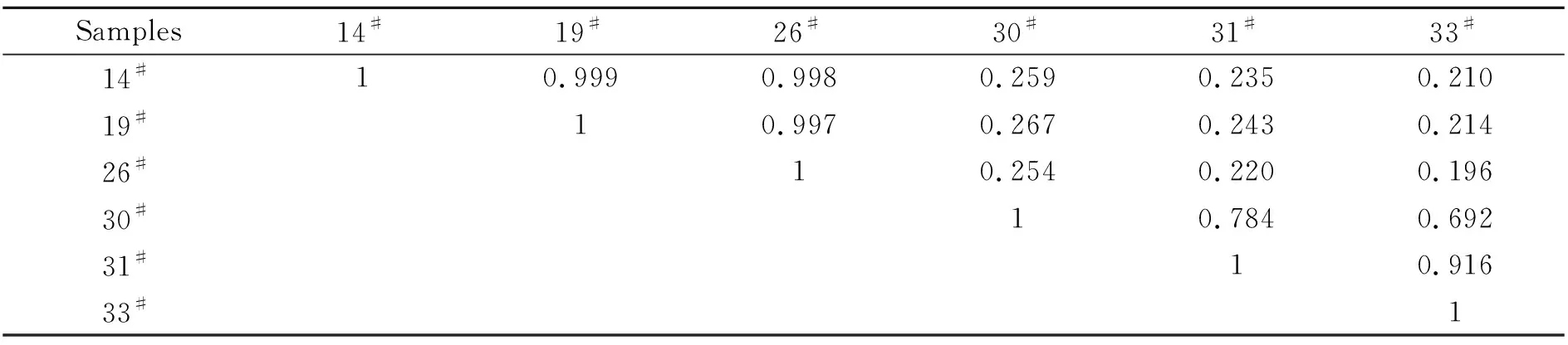
表2 6种样本相关性计算结果

3.3 Fisher判别分析

为进一步检验主成分分析分类结果是否准确，利用Fisher判别分析对35个一次性塑料餐盒样本进行分类，判别函数特征值摘要见表3。如表3所示，判别分析提取了三个特征函数，典型相关性(Canonical Correlation)可以很好地度量数据之间的相似性[15]，三个函数的典型相关性均大于0.99，表明所提取的三个函数与各类样本相关性极强[16]。函数1的特征值为557.294，占方差百分比的56.9%；函数2的特征值为354.414，占方差百分比的36.2%；函数3的特征值为67.020，占方差百分比的6.8%。前两个特征函数所占方差累计百分比为93.2%，其对于样本分类问题的解释能力远远大于函数3，因此分别选择函数1和函数2作为X轴和Y轴绘制判别分析联合分布图[17]，见图3。分析联合分布图可知，借助判别函数1和2将35个一次性塑料餐盒样本分为了4类，分类结果与主成分分析结果一致。为了防止过拟合，评估模型的泛化能力[18]，将样本主体作为训练集，轮流抽取单个样本作为测试集，借助留一交叉验证(Leave-One-Out-Cross-Validation)算法对分类结果进行交叉验证[19]，最终对97.1%的样本进行了正确分类，证明判别分析分类结果准确可靠。在判别函数1上主要将第1类、第2类、第4类样本区分开来，在判别函数2上将第3类样本与其他三类样本区分开来。4类样本组间重心明显分开，组内样本重心收缩靠拢，表明判别函数模型分类效果良好。若想实现未知样本的快速分类，可在该模型条件下将已知样本作为训练集，未知样本作为测试集进行自动判别分类。

表3 判别函数特征值摘要

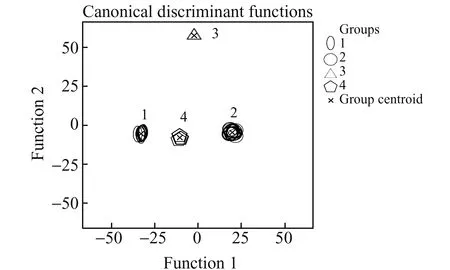
图3 根据函数1和2建立的联合分布图Fig.3 The joint distribution map based on functions 1 and 2

综上所述，35个一次性塑料餐盒样本分类结果见表4。

表4 35个样本的分类结果

4 结论

本实验对35个一次性塑料餐盒样本原始红外光谱图进行了多元散射校正等预处理，借助夹角余弦相似度对样本进行初步分类，但分类结果较为粗糙，不能准确反映样本所属类别关系。通过主成分分析和相关性计算，对样本的正确分类有了进一步的取舍，所绘制的三维散点图使得各样本与各类别之间的关系更加直观。最终借助Fisher判别分析，在检验前期分类结果准确性的同时构建了典型判别函数模型，该模型交叉验证正确率为97.1%，表明在该模型下能对新的未知样本进行模式识别分类。在后续的研究中，将引入感知神经网络等更为合理有效的模型，对样本的数据细节进行进一步的挖掘与探索。