基于遗传算法和支持向量机模型的高考成绩预测

金秀玲，卓艳如

(闽江学院 数学与数据科学学院，福建 福州 350108)

高考是由国家教育部统一组织的、国家或部分省份统一命题的、社会关注度极高且极其重要的考试，故根据模拟考试分数对高考分数进行预测有着重要的意义。

随着计算机技术的发展，机器学习中传统预测模型如线性回归、BP神经网络、模糊理论、支持向量机(SVM)等理论已被用于教育领域。有学者[1-2]研究发现高考成绩和模拟考试成绩虽然有一定的区别，但是也存在一定的关联，可以根据模拟考试成绩预测高考成绩。文献[3-5]挖掘了高招网的数据，利用线性回归和模糊理论预测高考录取分数线。周琦[6]利用高三学生平时成绩建立改进的决策树预测学生高考成绩和录取批次。张琼[7]利用高一新生的入学成绩建立Bayes网络对高考录取批次进行了预测。张莉等[8]运用SVM模型对江苏省海门市四中理科六次模考成绩进行挖掘来预测高考成绩和录取批次。武剑平[9]利用BP神经网络对学生高考分数进行了预测。

上述文献分析证实了机器学习在预测高考分数方面有良好的性能。然而，传统的算法在预测高考成绩时都有缺陷，预测的精度也有待提升。其中，SVM被广泛认为是一种普适且非常有效的学习方法，它基于结构风险最小化原则，在分类和回归问题上具有较好的稳定性和预测性。为了进一步提高SVM模型的预测精度，本研究引入遗传算法(GA)全局自主寻找最优的SVM参数组合，建立GA-SVM高考成绩预测模型，并将其应用到贵州省某高中2016届学生高三的4次模拟考试成绩数据中，从而预测其高考成绩。

1 GA-SVM预测模型

1.1 支持向量机算法(SVM)

SVM的核心思想是结构风险最小化原则，SVM算法对于非线性回归模型的泛化能力强。SVM通过核函数将输入低维的原始数据映射到高维的新特征空间，同时将非线性回归问题巧妙地转化成线性回归问题。SVM线性回归模型为

f(x)=wTx+b,

(1)

式中：w、b是待估参数。

利用松弛因子，可线性化的SVM回归模型可转化为凸二次函数规划问题，其最优化表达为

(2)

式中：ξ1i，ξ2i≥0，是松弛因子，i=1，2，…，n；C是惩罚参数，C>0；ε是容忍度。

引入拉格朗日因子，可以得到SVM非线性回归的对偶问题为

(3)

直接引入核技巧，核映射线性化非线性的问题，将SVM线性回归模型扩展到SVM非线性回归情景，最终得到SVM非线性回归模型的表达式为

(4)

1.2 用遗传算法(GA)寻找最优参数

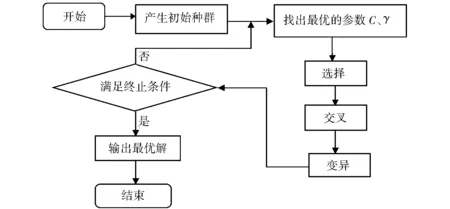
图1 GA-SVM流程Fig.1 GA-SVM flow chart

GA的特点是直接对结构对象进行操作，不受特定函数求导和函数连续性的限定，在全局采用概率化方法进行寻优，并能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。因此，可用GA来对RBF-SVM模型的参数组合C和γ进行优化。利用GA技术对RBF-SVM模型的参数(惩罚参数C和核函数参数γ)寻优时，先进行编码，然后在目标函数的约束下，通过随机选择、交叉和变异等步骤在全局寻找最优参数组合估计值，从而有效提高SVM高考分数预测的精度和效率。GA优化SVM模型寻优步骤如图1所示。

2 GA-SVM高考成绩预测模型

2.1 数据说明

实证分析数据来源于贵州省黔西县某高中2016届669名学生的4次模拟考试和高考分数，样本容量为669，数据维数是669×5。该校的生源在贵州省属于中等水平，多年来高考成绩比较稳定，数据真实可靠且具有较强的代表性。原始数据概况详见表1。从表1 可以清晰地看出：X1的均值为262，其他3次模拟考试和高考成绩均值在340左右；5个变量中位数都在350附近，它们的最大值取值在530左右，方差稳定在65附近。进一步通过箱线图(见图2)观察出预测变量和高考成绩数据的范围基本一致，方差也一致，所以建模时不需要对变量进行标准化。

对原始变量进行相关性分析，得到的结果见表2。其中，每次模拟考试分数与高考分数之间的相关系数为0.799 1～0.870 8，具有很强的相关性，可见模拟考试成绩对于高考而言具有很强的指导意义。对收集的669个学生的4次模拟考试成绩和高考成绩数据，其中569个数据作为训练集，剩余的100个数据作为测试集，用GA算法优化后的SVM算法对高考成绩进行预测。

表1 原始数据概况Tab.1 Raw data overview

图2 原始变量的箱线图Fig.2 Boxplot of the original variable

表2 相关系数Tab.2 Correlation table

2.2 基于GA-SVM算法的高考成绩预测

图3 参数优化过程Fig.3 Parameter optimization process

利用GA-SVM 算法对569个学生的高考成绩进行预测，使用5折交叉验证，重复测试10次。GA-SVM模型参数中，种群50个，进化100代，SVM模型惩罚参数C设置为[0.000 1，100]，高斯核函数参数γ设置为[0.001，50]。以第一次对569个学生成绩数据使用5折交叉验证为例，图3给出了使用GA-SVM算法优化支持向量机的参数进化运算曲线。

遵循GA最优选择法则，种群中的最优个体适应度逐渐减少，最终趋于716.352 4，此时惩罚参数C与核函数参数γ的组合达到性能最优，即当最佳惩罚参数C=6.549 266、最佳核函数参数γ=0.480 225 30时，训练集的均方误差为616.121 2、测试集的均方误差为713.581 7，结果见表3。重复测试10 次，得到GA-SVM高考成绩预测训练集均方误差平均值为616.345 6、测试集均方误差平均值为715.453 2。

表3 基于GA-SVM模型的高考成绩预测结果Tab.3 GA-SVM model predicting results of college entrance examination

3 结果与分析

引入多元线性回归模型、SVM和BP神经网络模型分别对569个学生的高考成绩进行建模，使用5折交叉验证，重复测试10次，计算10次均方误差的平均值，结果见表4。

表4 多元回归、BP神经网络、SVM模型与GA-SVM模型结果的比较Tab.4 Comparison of results of multivariate regression, BP neural network, SVM model and GA-SVM model

通过对比表4中的数据可知，GA-SVM模型在训练集的平均MSE和测试上的平均均方误差都是最小的，预测效果优于多元线性回归、BP神经网络和SVM模型。这是由于GA经过遗传、交叉、变异步骤不断对SVM的参数C和γ进行调整，最终得到全局最优参数组合，从而使得GA-SVM模型在预测高考成绩时，精度高于多元回归、BP神经网络和SVM等传统方法。

4 结语

以贵州省某高中2016届669名学生的4次模拟考试成绩和高考成绩为研究对象，提出了基于GA-SVM模型预测高考成绩的方法。该方法能够解决SVM算法在回归过程中主要依靠经验来选取参数的问题，通过GA对SVM中的参数进行全局自主优化和调整，最终获得最优参数组合。

采用GA-SVM模型对比多元回归、BP神经网络模型分别对测试集数据进行高考成绩预测，结果表明：GA-SVM模型测试集的均方误差最小，明显优于多元回归、BP神经网络模型和SVM模型等传统回归算法。因此，在已知模拟考试成绩后，GA-SVM模型能够预测学生高考分数的趋势，并利用预测分析结果帮助学生了解自己的不足之处，及时调整高考复习策略。同时，教师可以根据预测结果在后期制定针对性强的教学计划，做到个性化教学。