基于前景理论的毕达哥拉斯模糊TOPSIS法及其决策应用

常 娟，刘卫锋

(郑州航空工业管理学院 数学学院，河南 郑州 450046)

1986年，Atanassov[1]提出了直觉模糊集(IFS)，利用隶属度和非隶属度描述肯定和否定程度，从而能够更全面地描述模糊信息。直觉模糊集要求隶属度和非隶属度之和不大于1，但是在决策过程中，当独立给出满足属性的隶属度和非隶属度时，会有二者之和超过1的情况发生，此时若不修改属性信息，则直觉模糊的决策理论和方法是无法适用的。2013年，Yager等[2-3]在分析直觉模糊集补运算的基础上，提出复杂条件下可将隶属度与非隶属度放宽至平方和不超过1，由此给出了直觉模糊集的最新推广——毕达哥拉斯模糊集(PFS)。显然，与IFS相比，PFS是刻画模糊信息更有力的工具。 近几年来，研究者们对PFS表现出很大的兴趣，也取得了许多研究成果。 Zhang等[4-5]提出毕达哥拉斯模糊数(PFN)的概念，并定义了PFN的运算和距离、得分函数、精确函数及相似度；Peng等[6]定义了PFN的除法和减法运算；李德清等[7]则称PFN为勾股模糊数，比较了勾股模糊数的3种排序方法，并定义了勾股模糊数的几种距离测度。在决策方法方面：文献[4]和文献[7]将TOPSIS法推广至PFN环境；Ren等[8]提出了毕达哥拉斯模糊环境下的TODIM法；Zhang[9]提出了区间毕达哥拉斯QUALIFLEX法。在毕达哥拉斯集成算子方面：刘卫锋等[10-11]定义了PFN的一系列集成算子，如加权平均(PFOWA)和加权几何(PFOWG)算子、拟有序加权算子和毕达哥拉斯模糊交叉影响算子；Garg[12]提出了Einstein运算下的毕达哥拉斯模糊集成算子；Wu等[13]、彭定洪等[14]分别提出了毕达哥拉斯模糊Hamacher集成算子和优先集结算子；常娟等[15]研究了考虑属性信息分布的毕达哥拉斯密度算子。此外，关于毕达哥拉斯拓展形式的研究中，毕达哥拉斯模糊软集[16]、毕达哥拉斯模糊语言集[17-18]、毕达哥拉斯犹豫模糊集[19-20]等相继展开并用于解决不同模糊环境下的决策问题。

以上关于毕达哥拉斯的决策成果大多是在假设决策者完全理性的情况下给出的，但在实际决策过程中,决策者存在的非理性心理、对风险的偏好等都会对决策结果产生影响。为此，Kahneman等[21-22]提出了著名的前景理论，目前已得到广泛研究和应用。李鹏等[23]针对指标权重未知的随机直觉模糊决策问题，提出了基于前景理论和新的记分函数的随机决策方法；Li等[24]、王应明等[25]则提出前景理论与TOPSIS相结合的决策方法并分别应用于直觉梯形模糊、犹豫模糊环境；Peng等[26]提出了基于前景理论的TODIM和PROMETHEE法；Zhou等[27]则将前景理论用于研究投资组合群决策问题；罗承昆等[28]针对混合型多属性决策问题，提出了基于前景理论和证据推理的决策方法。

受文献[24]和文献[25]的启发，针对属性信息为PFN的多属性决策问题，本研究提出了基于前景理论的TOPSIS决策方法。首先，对文献[4]和文献[7]所提的毕达哥拉斯模糊TOPSIS法进行对比分析，并指出存在的问题，提出解决的方法；其次，提出毕达哥拉斯模糊数的前景价值函数，并将正、负理想方案作为参考点，通过计算各方案的收益-损失比对各方案进行优劣排序；最后，通过一个算例对所提方法的可行性与有效性进行了验证。

1 基本概念

1.1 毕达哥拉斯模糊数

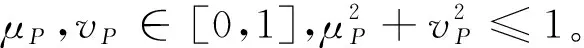
若将PFN的隶属度和非隶属度看成二维坐标系的横坐标和纵坐标，则根据文献[2]给出刻画PFN长度和方向的量。

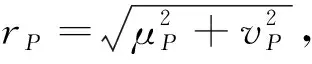
基于以上定义，毕达哥拉斯模糊数又可表示为P=rPeiθP，并称为∏-i型模糊数。

定义3设A，B∈PFNs，且A=<μA，vA>，B=<μB，vB>，λ>0。定义如下运算：

关于PFN大小的比较，文献[2]提出了排序函数值, 根据排序函数值的大小确定PFN的大小。

对于任意的P1=<μP1，vP1>，P2=<μP2，vP2>∈PFNs，则

(1)若V(P1)>V(P2)，则P1P2；(2)若V(P1)=V(P2)，则P1=P2。

文献[4]和文献[5]将直觉模糊数的得分函数和精确函数推广至PFN，并以此作为比较PFN大小的依据。

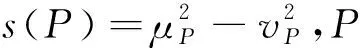
设P1=<μP1，vP1>，P2=<μP2，vP2>∈PFNs，则

(1)当s(P1)>s(P2)时，P1P2；

(2)当s(P1)=s(P2)时，若h(P1)>h(P2)，则P1P2；若h(P1)=h(P2)，则P1=P2。

文献[7]提出在比较P1=<0.5,0.1>和P2=<0.6,0.3>时，如果将P1、P2作为直觉模糊数，则利用得分函数可得P1P2，而作为PFN时，由定义5的方法可得P2P1，由定义4的方法可得P1P2。因此，文献[7]认为定义5所提的方法不够科学。

关于毕达哥拉斯模糊数的距离，文献[4]给出如下定义：

定义6设A=<μA，vA>，B=<μB，vB>∈PFNs，定义A、B的距离为

文献[7]认为上述距离的定义只考虑了隶属度、非隶属度和犹豫度，并且通过例子说明了上述定义的不合理性。事实上，PFN主要由隶属度、非隶属度、自信度、自信度方向4个因素决定。因此，李德清等给出了如下PFN的距离测度：

定义7设A=<μA，vA>，B=<μB，vB>∈PFNs，常数q>0。则

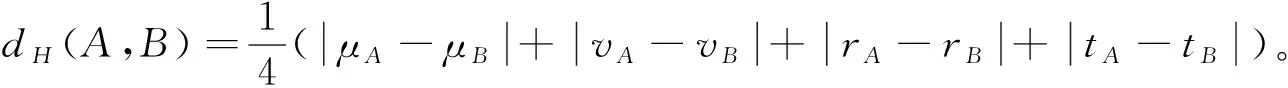
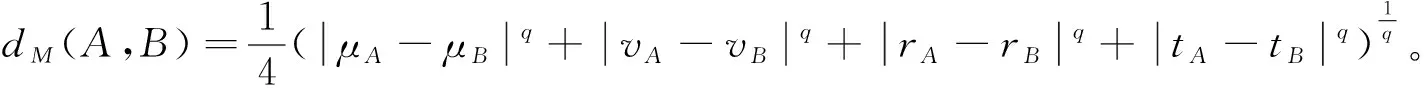
1.2 前景理论

在实际决策中，决策者会出现在面临损失时偏好风险、面临收益时厌恶风险的“有限理性”行为。文献[21]和文献[22]提出了前景理论和累积前景理论。前景理论中的前景价值由价值函数和概率权重函数确定，而前景价值函数是决策者根据实际收益或损失所产生的主观感受价值。1992年，文献[22]等提出如下形式的价值函数:

定义8设数x偏离某一参考点x0的大小为Δx，且Δx≥0表示x相对于x0获得收益，Δx≤0表示遭受损失，记x的价值函数

式中：参数α>0和β<1分别表示决策者对收益和损失的敏感程度；参数θ>1表示相对于收益，决策者对损失更加敏感。

Kahneman等通过经验数据认为，通常可取α=β=0.88、θ=2.25。

下面将上述定义推广至毕达哥拉斯模糊环境，提出毕达哥拉斯模糊前景价值函数。

定义9设毕达哥拉斯模糊数P1、P2，若以P2为决策参考点，则P1的前景价值函数为

式中：d(P1，P2)为P1、P2的距离；参数α>0，β<1，θ>1。

2 基于前景理论的毕达哥拉斯模糊TOPSIS法

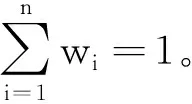
2.1 文献[4]与文献[7]的方法比较

文献[4]和文献[7]都将TOPSIS法推广至毕达哥拉斯模糊环境，但是二者的方法存在以下区别：

(1)选取正、负理想方案的方法不同。文献[4]利用PFN的得分函数确定正、负理想方案，即

而文献[7]则利用排序函数值作为选取依据，即

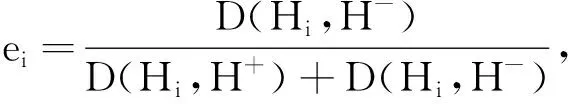
以上两种方法都是对TOPSIS法的拓展性研究，丰富了毕达哥拉斯模糊决策方法理论，但是也存在以下问题：

(1)在确定正、负理想方案时，利用得分函数或排序函数值会得到不同的结果。例：考虑毕达哥拉斯模糊数集{<0.6，0.3>，<0.5，0.3>，<0.7，0.4>，<0.6，0.6>}，如果利用得分函数则最优为<0.7，0.4>，而利用排序函数值则最优为<0.6，0.3>。模糊数的比较本身就是有争议的，无论是采取得分函数还是排序函数值得到的最优结果都是带有主观因素的。

(2)两种方法都是在决策者完全理性的条件下考虑的，而实际决策过程中，决策者对风险是有偏好的，是有限理性的。因此，考虑决策者实际风险偏好的毕达哥拉斯决策问题是有实际背景和意义的。

2.2 基于前景理论的毕达哥拉斯模糊TOPSIS法

为解决以上问题，首先,在确立正、负理想方案时，要采取更为客观的方法，直接从原始信息中构造正、负理想方案，避免因采用不同的标准而得到不同的结果。其次，考虑到决策者的风险态度，通过计算各方案到正、负理想方案的前景价值函数，从而得到收益-损失比，以此替代贴近度对各方案进行择优排序。下面提出基于前景理论的毕达哥拉斯模糊TOPSIS法。具体步骤如下：

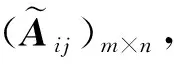
步骤2确定正理想方案H+和负理想方案H-，其中

以上确定正、负理想方案的方法，可以保证无论是在得分函数还是在排序函数值下，各属性值都是最优或者最劣的。

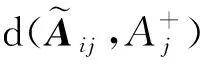
步骤4由于各方案的属性值相对于正理想方案都是损失的，相对于负理想方案都是获益的，设Hi相对于H+的综合损失值为Φ-(Hi)，相对于H-的综合收益值为Φ+(Hi)，则由定义9, 可得

3 决策应用

3.1 决策算例

随着我国社会经济的快速发展，飞机成为人们出行的重要选择。目前，随着航空市场的完善，以及我国高铁的全面覆盖，航空公司间的竞争也日趋激烈。为了争取更多的客源，各航空公司在保证同质量的基本服务之外，提高特色服务质量成了竞争的重要手段。因此，对我国航空公司服务质量的评估有重要的实际意义。假设现在对4家航空公司(H1、H2、H3、H4)进行航空服务质量评价和排序。邀请相关领域的专家并随机选取客户进行调研，从票务服务(u1)、登机服务(u2)、空中客舱服务(u3)、中转/联程服务(u4)4个方面对各航空公司进行评价，并以毕达哥拉斯模糊数的形式给出评估值。如H1在u1下的评估值为<0.9,0.3>，表示满意度为0.9，不满意度为0.3。类似地，其他属性值如表1所示。各属性权重向量为w=(0.15,0.25,0.35,0.25)。

表1 毕达哥拉斯模糊决策矩阵Tab.1 Pythagorean fuzzy decision matrix

步骤1由于各属性准则均为效益型，而且各属性信息量纲相同，故不需要对表1进行规范化处理。

步骤2确定正、负理想方案，如表1所示。

步骤3由定义7计算各方案与正、负理想方案相应属性值的距离(比如选取海明距离)，则得到距离矩阵如表2和表3所示。

表2 各方案属性信息到H+的距离 Tab.2 Distance from attribute value of each scheme to H+

表3 各方案属性信息到H-的距离 Tab.3 Distance from attribute value of each scheme to H-

步骤4计算各方案相对于H+的综合损失值与相对于H-的综合收益值。取参数α=β=0.88，θ=2.25。

首先，利用表2中H1和H+各属性值的距离，得到H1相对于H+的综合损失值：

Φ-(H1)=-2.25(0.15·0.048 10.88+0.25·0.2280.88+0.35·0.425 60.88+0.25·0.057 00.88)=-0.593 1。

类似地，利用表3中H1和H-各属性的距离，得到H1相对于H-的综合收益值：

Φ+(H1)=0.15·0.376 80.88+0.25·00.88+0.35·00.88+0.25·0.193 20.88)=0.122 4。

其他方案的综合损失值和综合收益值可做类似计算，具体结果如表2和表3所示。

步骤5计算各方案的收益-损失比分别为

s1=0.206 4，s2=1.203 7，s3=0.688 7，s4=0.704 2，

则各航空企业的排序结果为H2H4H3H1。

3.2 算例分析

首先，考虑到态度参数对决策结果的影响，分别令α、β取不同的值，当θ=2.25时，利用所提方法得到排序结果，如表4所示。

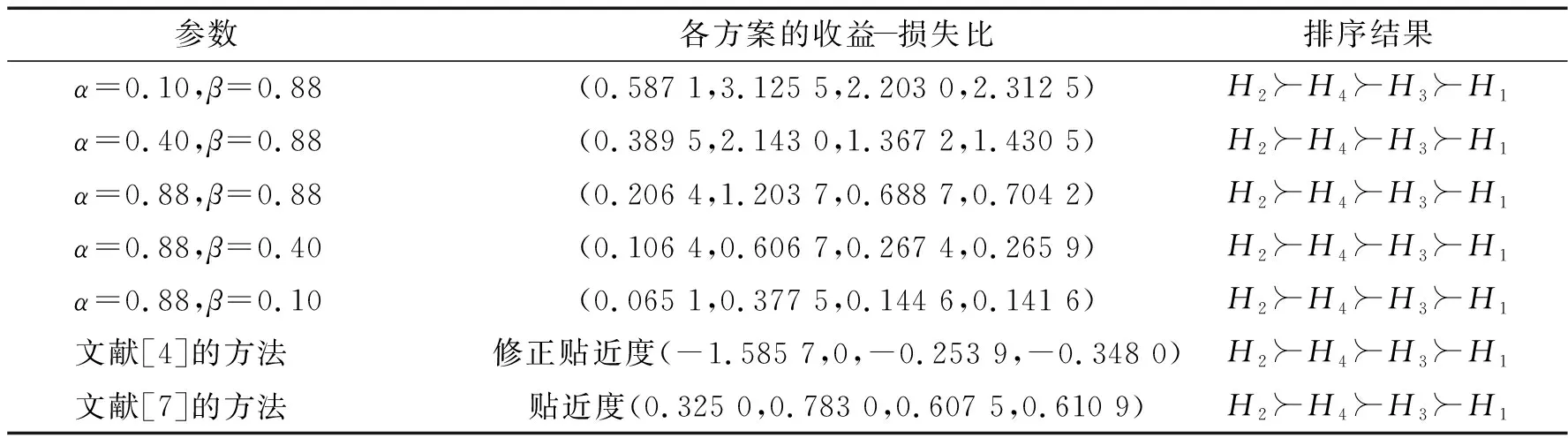
表4 θ=2.25时，不同参数下的排序结果 Tab.4 When θ=2.25, the sort results under different parameters

由表4可见，随着α增大、β减少，H2的收益-损失比与其他企业的差距越来越大，其排序第一的优势地位越来越凸显。这表明决策者更看重收益，而忽略损失的风险。相应地，各企业的排序发生了变化，但是最优企业均为H2，最劣企业均为H1，从表1的原始信息可以看出，H2的各属性值有明显的优势，而H1的各属性值有明显的劣势。因此，本方法在体现决策者风险态度的同时，是符合客观事实的。

其次，与本方法提出的当参数α=β=0.88、θ=2.25时的结果相比，文献[4]的方法排序结果不同，这是由于确定正、负理想方案，以及使用距离测度不同，并且本方法考虑了决策者风险态度。而文献[7]的方法结果与本方法结果是一致的。但是如果对本方法所得的收益-损失比归一化可得(0.073 6，0.430 7，0.245 7，0.251 2)，而将文献[7]的贴近度归一化可得(0.139 7，0.336 6，0.261 1，0.262 6)。可见相比贴近度，收益-损失比中H2得到明显提升，H1明显下降，H3、H4之间的区分度也更明显。这体现了决策者风险态度因素确实对决策结果产生了影响，表明本方法是有效的。

4 结语

针对属性值为毕达哥拉斯模糊数的多属性决策问题，对已有的TOPSIS法进行比较分析，指出了存在的问题。考虑到决策者的有限理性行为，提出了基于前景理论的毕达哥拉斯模糊TOPSIS法。该方法考虑了实际问题中人们对收益和损失的风险偏好，通过计算方案到正、负理想方案的收益-损失比对各方案排序。算例分析表明本方法是有效、可行的，是对毕达哥拉斯模糊决策方法的补充，可用于供应商选择、行业评估等多种实际决策问题。