多无人机自适应编队协同航迹规划

许 洋 ，秦小林 *，刘 佳 ，张力戈

（1.中国科学院成都计算机应用研究所，成都610041； 2.中国科学院大学计算机与控制学院，北京100080）

（∗通信作者电子邮箱qinxl2001@126.com）

0 引言

无 人 机（Unmanned Aerial Vehicle，UAV）航 迹 规 划（trajectory planning）是指在初始状态、任务目标、威胁区和一些已知环境信息的情况下获得性能最优的规划问题，是任务规划系统的关键技术之一。目前单机航迹规划技术已经相当成熟，然而在未来战场，多无人机编队协同执行任务将成为主要的作战形式，而协同航迹规划是提高无人机协同作战效能，保证无人机协同作战顺利实施的关键。多无人机协同航迹规划在为各无人机规划出满足约束条件的最优航迹时，还需考虑各无人机之间的空间协同性以及时间协同性［1］，其主要任务包括航迹规划、碰撞避免、队形形成/重构以及队形保持等。

目前，针对多无人机协同航迹规划问题，主要采用的算法包括人工势场法（Artificial Potential Field，APF）［2-3］、粒子群优化（Particle Swarm Optimization，PSO）算法［4］、滑模控制［5］、PID（Proportion Integration Differentiation）［6-7］等。文献［1］采用协同非支配排序进化算法，根据多架无人机的航行距离、安全性、时间以及空间的协同性进行规划；文献［8］采用混合粒子群优化算法与遗传算法相结合的方法，实现了对多无人机编队重构过程中参数最优化问题的求解；文献［9］通过引入分布式结构和层次网络，并基于由指挥官、虚拟领航者和跟随者组成的多无人机系统建立无人机协同机制，实现了多无人机自主编队和重组任务；文献［10］采用任务分配和粒子群优化算法，实现了对无人机群编队转换的高效策略。以上几种方法都是针对无障碍环境下多无人机的编队协同控制问题。

为了确保复杂环境下多无人机编队能够安全、快速到达任务区域，需要设计满足一定约束条件及性能指标最优的编队航迹。文献［11］利用共识的几何优化方法，结合分布式策略，实现了在包含静、动态障碍物的二、三维环境中，求解一组机器人协同控制的最优参数；文献［12］通过建立多无人机系统的特殊正交群（Special Orthogonal group）SO（3）控制模型，实现了多无人机在姿态一致的状态下以期望的队形稳定飞行；文献［13］采用神经网络方法，自适应地逼近和在线补偿动态逆误差，提高了多无人机队形的稳定性；文献［3，14-15］采用了人工势场法解决复杂环境下的编队控制及避障问题，通过各无人机之间的斥力与引力相互作用，实现整个协同任务，然而复杂环境下的避障动作会在一定程度上扰乱无人机编队队形，影响编队的稳定性。

基于滚动时域优化思想的模型预测控制（Model Predictive Control，MPC）策略能够显式地考虑各种约束条件，并滚动实施控制输入，具有鲁棒性较强等特点，因此在多无人机编队控制等问题中得到了广泛应用［16］；文献［17］利用分布式模型预测控制（Distributed Model Predictive Control，DMPC）对计算得到的参考轨迹进行跟踪，并对障碍物进行碰撞检测，通过加入惩罚项实现动态航迹跟踪及避障；文献［18］采用DMPC方法将编队重构问题转化为滚动在线优化问题，并采用微分进化（Differential Evolution，DE）方法进行求解。

然而上述工作主要集中在单一编队队形控制、编队飞行避障控制等方面，未考虑复杂环境下多无人机编队队形的适应性以及队形转换的高效性。

本文针对以上问题，提出了一种基于自适应分布式模型预测控制的快速粒子群优化（Adaptive Distributed Model Predictive Controller-Fast Particle Swarm Optimization，ADMPCFPSO）方法。该方法利用虚拟结构法与领航跟随法相结合的编队策略，构造出自适应虚拟编队引导点，并设计基于最小代价函数的优化目标；采用分布式模型预测控制方法将其转化为滚动在线优化问题，通过快速粒子群优化（Fast Particle Swarm Optimization，FPSO）算法对问题进行求解。仿真结果表明，该方法可以高效解决复杂环境下的多无人机协同航迹规划问题，与基于人工势场法的编队协同控制方案［3］相比，航迹规划的平均消耗时间降低了31.6%。

1 相关工作

1.1 模型预测控制

模型预测控制是一种基于滚动时域的在线优化控制策略，其基本思想是，假设当前时间点为k，在有限时域［k，k+j］，通过使某一性能指标最优化来确定其未来的控制作用，选择第一个最优控制输入作为当前的控制输入，在下一时刻k+1，计算［k+1，k+j+1］的控制输出，重复以上过程，直到任务完成。其原理如图1所示。

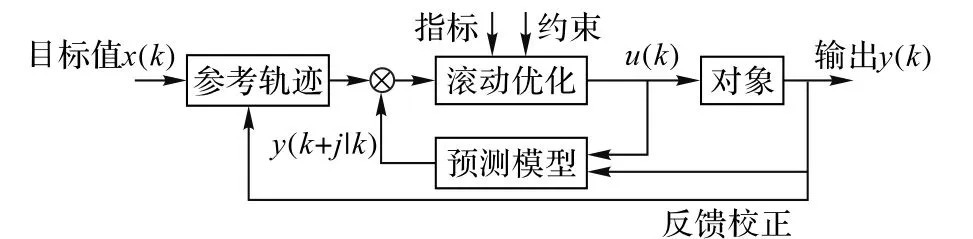
图1 模型预测控制原理框图Fig.1 Functional block diagramof model predictivecontrol

1.2 粒子群优化

粒子群优化（PSO）算法［4］是由美国 Kennedy和Elberhart于1995年，受到鸟群觅食的行为启发而提出的，是一种模拟鸟类飞行过程中群聚行为的智能优化算法。

由m个粒子组成的群体在超维空间内以一定的速度飞行，每个粒子表示问题的一个解。粒子在优化过程中，跟随两个极值实现自身的迭代。一个是粒子自身找到的历史最优解，称为个体极值；另一个是整个群体找到的最优解，称为全局极值。粒子的速度和位置更新公式分别为：

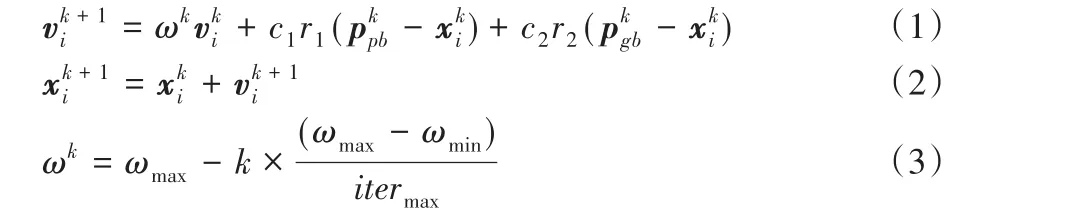
式（1）是PSO的速度更新公式，其中表示第i个粒子在第k次迭代时的速度；c1和c2为学习因子；r1和r2是[0，1]区间内均匀分布的随机数；ω为惯性权重，表示粒子对原有速度继承的程度；式（2）是位置更新公式，表示第i个粒子在第k次迭代时的位置；式（3）为惯性权重的更新公式，其中ωmin为最小权重；ωmax为最大权重；itermax为最大迭代次数。

2 问题描述

假定在某次任务中，由n（n＞1）架无人机组成的编队从某一起始区域飞往目标区域执行任务。以多旋翼无人机为例，讨论其由初始状态（初始区域）出发，以最小代价到达目标区域。在此过程中，需要综合考虑飞行环境中的威胁、无人机自身性能以及编队控制等约束条件，为各无人机实时规划航迹。因此，提出以下两个假设。

假设1 在航迹规划过程中，将单个无人机看作质点，多无人机编队需考虑编队宽度；线性编队属于特例，不考虑宽度。

假设2 多无人机在宽阔区域，保持特定的编队飞行，增大侦察范围，从而减小可能存在的风险；在狭窄区域，无需考虑侦察范围，以线性编队飞行，保证多无人机安全通过该区域。

2.1 协同控制架构

多无人机协同控制架构包括全局航迹规划系统和自适应编队协同系统，如图2所示。全局航迹规划系统主要根据部分已知环境信息，预先计算全局代价图，在满足相应的约束条件（自身动力学约束、编队队形约束、环境约束等）下，利用ADMPC-FPSO动态规划航迹，引导整个编队以最低代价从初始区域前往目标区域。

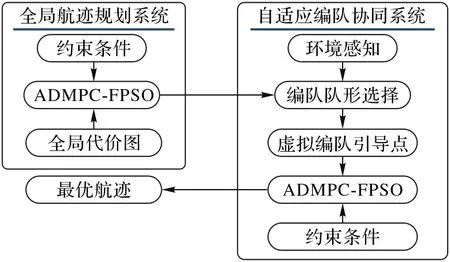
图2 多无人机协同控制架构Fig.2 Framework of multi-UAV cooperative control

自适应编队协同系统是以虚拟编队引导点为主的编队控制策略。无人机编队通过感知环境（通道宽度），选取合适队形，结合虚拟编队引导点与ADMPC-FPSO，在满足所有约束条件下，动态规划最优航迹并保持特定的队形。规划过程中，编队队形之间的变换通过改变虚拟编队引导点实现。

2.2 编队飞行中全局航迹规划问题

为满足假设2，在航迹规划过程中，若只考虑某一固定编队，可能因部分狭窄区域只允许线性编队通过，而造成该区域被忽略，大大增加全局代价，导致最终无法得到全局最优航迹。

利用“领航者-跟随者”结构（后文，将该结构中的“领航者”统称为“领航无人机”，而“跟随者”统称为“跟随无人机”），在全局航迹规划过程中，主要对领航无人机进行动态航迹规划。领航无人机处于编队的中间位置，在非线性编队的情况下，规划过程必须考虑无人机编队宽度约束，即领航无人机与任一障碍物的距离至少保持编队宽度的一半。当无人机进入狭窄区域，编队变换为线性编队，此时可不考虑编队宽度，从而尽可能减少全局代价。

在上述约束条件下，可将其看作单独地对领航无人机的航迹规划问题。

2.3 基于虚拟编队引导点的编队变换及控制

在本文中，主要考虑线性编队和三角编队之间的变换，如图3所示。在自适应编队变换过程中，首先根据领航无人机的状态信息，选取合适编队，并计算虚拟编队引导点。而后跟随无人机前往其对应的虚拟编队引导点，实现编队变换。

在形成虚拟编队引导点后，对各跟随无人机来说，与2.2节中描述的问题类似，只需将虚拟编队引导点作为各对应跟随无人机的临时目标位置即可。

各无人机的规划相互独立，通过建立通信保证实时信息交互，以实现对各无人机的分布式控制。

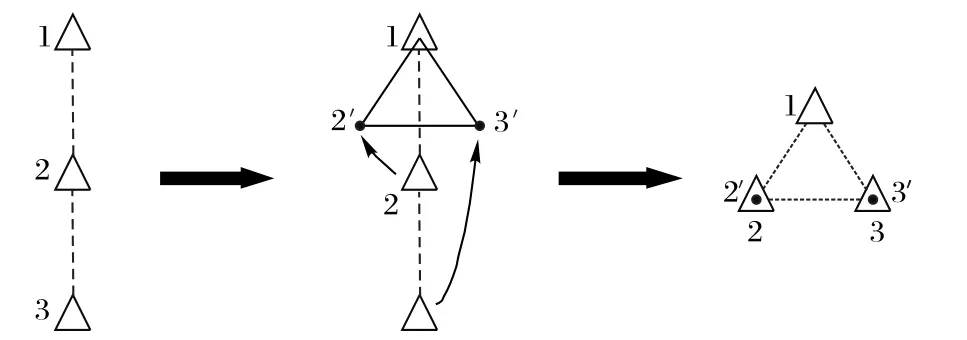
图3 多无人机编队变换示意图Fig.3 Schematic diagramof multi-UAVformationtransformation

3 数学模型

3.1 无人机动力学模型

在飞行过程中，假定无人机在短时间内保持在同一高度飞行，其二维质心运动方程［17］为：

式中：（xi，yi）为无人机i的二维坐标；V表示飞行速度；ψ̇i为航向角；ui为对应的控制量。控制量与航向角约束为：

3.2 航迹规划目标函数模型设计

多无人机系统中，对各无人机建立的数学模型一致，区别在于目标位置的选取，其线性时不变系统动力学可统一描述为：

式中：x(k)∈ RNx是状态向量，u(k)∈ RNu是输入向量；式（5）为无人机的状态空间模型，式（6）为状态和输入需要满足的约束条件；其中γ(k)为k时刻需要满足的约束条件，输出向量y(k)∈ RNy。

一般的目标函数，采用如下形式：

式中：l(∗)是代价函数，χF是目标集。

在航迹规划过程中，当控制输入被执行，形成新的状态，基于该状态进行下一步优化，产生新的控制输入，循环执行直到任务结束。采用MPC算法，基于滚动时域框架的优化描述为

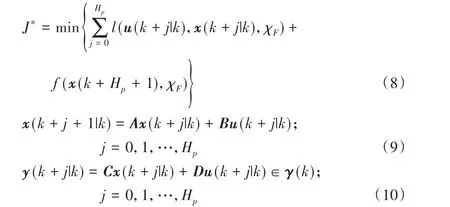
3.3 自适应虚拟编队引导点

本文采用虚拟编队引导点方法完成自适应编队飞行控制任务，如图4所示，以三个无人机为例，UAVleader为领航无人机，UAVfollower#1和UAVfollower#2为跟随无人机所对应的虚拟编队引导点，引导点沿无人机运动方向对称分布，领航无人机输入向量为（ulx，uly），UAVfollower#i的坐标为(xfi，yfi)，编队半径为rf。

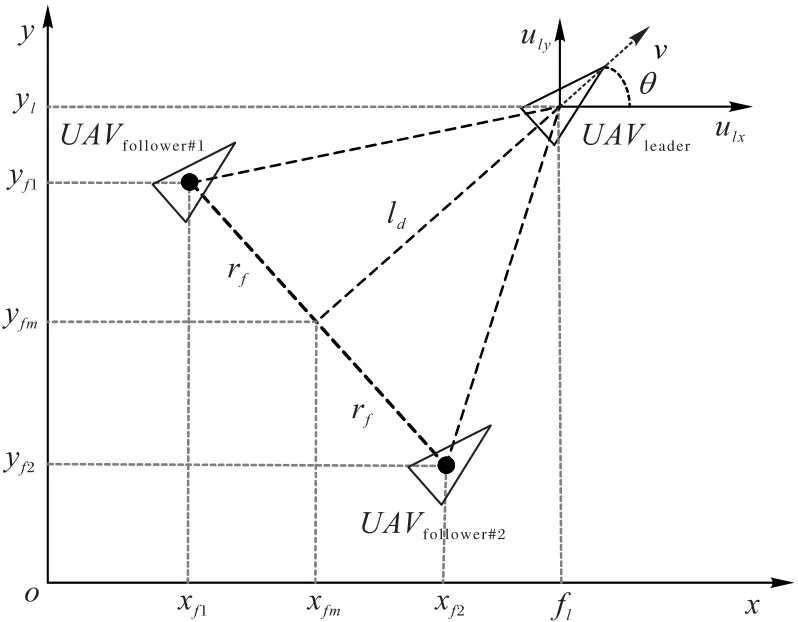
图4 虚拟编队引导点坐标系Fig.4 Virtual formation guidepoint coordinatesystem

由于本文针对多旋翼无人机飞行控制，在飞行过程中，领航无人机可能会出现转弯角度较大的情况，为避免出现大幅度甩尾情况，对ld做如下处理：

式中cld为减幅权重。

结合式（11）、（12）、（13），求出虚拟编队引导点中UAVfollower#1和UAVfollower#2的坐标。

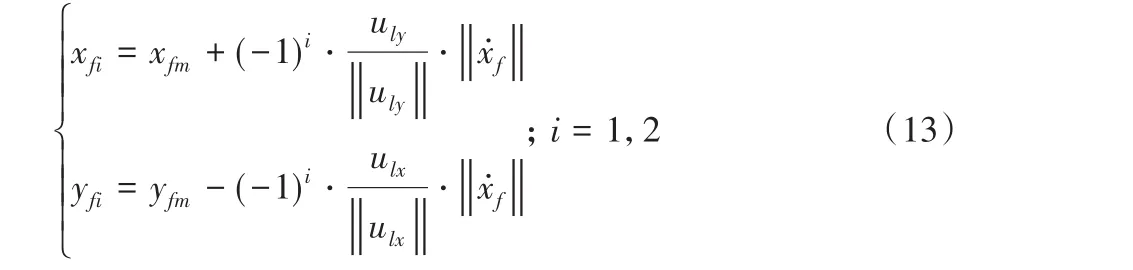
式中(xfi，yfi)为第i个虚拟引导点的坐标。

通过自适应调节rf值，可在一定程度上提高复杂环境下编队的适应度。假设检测前方通道宽度为Rdet，那么：

若Rdet＜Rmin，则变换为线性编队。Rmin为无人机之间的最小安全距离；φ为保证无人机飞行安全的一个极小值。

3.4 多无人机编队通信拓扑模型

本文采用图论对无人机之间的通信拓扑关系进行描述，设G（V，E，A）表示一个加权无向图，其中：V是图的顶点集，E是图的边集，A=(aij)N×N称为图的邻接矩阵。在多旋翼编队飞行问题中，将每一个无人机看作图的一个顶点，无人机之间的信息交互连接就可以用图G相应的边来表示。若aij＞0，则表示边(j，i)∈E，即第i个无人机能够从第j个无人机获得所需信息，否则aij=0。由此可以定义顶点i的邻居集为Ni={j∈V|(j，i)∈E}。

如图5所示，在无人机的整个通信拓扑结构中，各无人机只与距离其半径r以内的无人机建立通信，完成信息交换，满足以下公式：

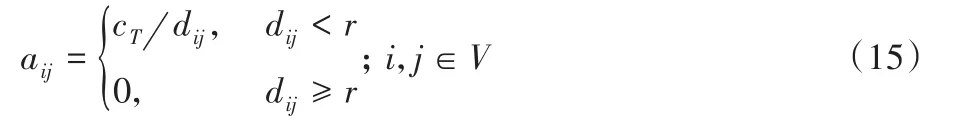
式中：d ij为i与j之间的距离，r为无人机的通信半径。

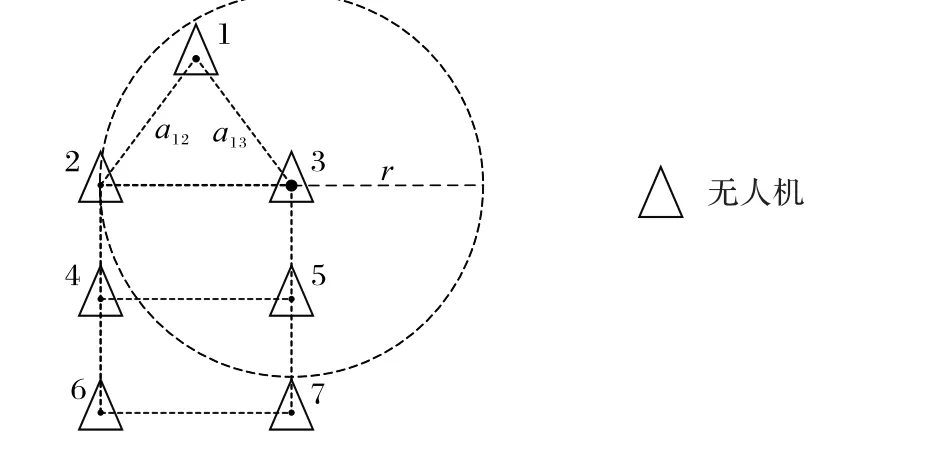
图5 多无人机编队通信拓扑示意图Fig.5 Multi-UAV formation communication topology

4 ADMPC-FPSO自适应协同航迹规划

多无人机协同航迹规划主要分为全局航迹规划和自适应编队协同控制两部分。全局航迹规划可简单看作对领航无人机的航迹规划过程，与单个无人机不同，这里必须考虑编队宽度的约束。对此，本文通过扩充障碍物的方法实现可视点迁移，以此满足编队协同控制的相应约束条件。

编队全局航迹规划过程主要包括两个阶段：第1阶段为代价评估阶段，根据当前环境生成代价图，利用计算得到的代价图来表示航迹端点到目标点的代价估计；第2阶段为实时航迹规划阶段，在问题描述中，已经将航迹规划表示成一个优化问题，在此主要是基于ADMPC-FPSO实时航迹规划的一个优化过程。

自适应编队协同控制主要包括两个阶段：第1个阶段为虚拟编队引导点的形成，根据无人机所处环境与自身状态，自适应选取并计算最优虚拟编队引导点的位置，为编队队形的形成、保持及变换提供前提条件；第2阶段为各无人机在整个多无人机系统中，基于ADMPC-FPSO协同完成编队队形的形成、保持及变换任务。

4.1 代价图

根据第1章可知，从航迹规划全局看，粒子群优化有可能陷入局部最优。因此，需要预先进行合理的代价转换，如文献［18］中提到的代价图方法，利用可视图［19］和Dijkstra［20］单源最短路径算法，搜索从目标点到各个点的最短路径。

对于领航无人机，由第3章可知，航迹端点为x(k+Hp+1)，因此基于代价图的终端惩罚项f(∗)可以表示如下：

式中：xvis为基于代价图的可视点；d(x(k+Hp+1)，xvis)为航迹端点到可视点的代价；Cvis为可视点到目标点的代价。

对于跟随无人机，在满足相应的约束条件，其规划过程实际上是局部的，因此终端惩罚项如下：

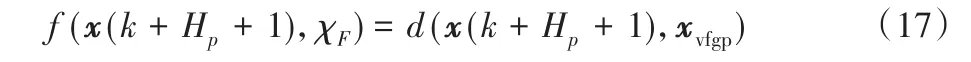
式中：xvfgp为对应的虚拟编队引导点；d(x(k+Hp+1)，xvfgp)为航迹端点到对应虚拟编队引导点的代价。

4.2 基于ADMPC-FPSO协同航迹规划

协同航迹规划是复杂约束条件下的最优化问题，采用粒子群优化算法进行航迹规划时，迭代初期，控制输入和状态可能存在违反约束的情况，算法需要迭代若干次才能产生满足要求的输入，并在此基础上进一步寻优。为提高算法的效率，本文根据粒子违反约束的程度来更新粒子。

在1.1节中对MPC进行了介绍，实际应用过程中，MPC分为集中式和分布式两种。集中式在多无人机编队飞行控制中，随着无人机数量的增加，其求解复杂度、通信量急剧增长。实际上，各无人机的动力学特性互相解耦［21］，无人机可以通过各自的约束和状态条件进行独立控制，故适于采用DMPC结构进行协同控制。

4.2.1 评价函数设计

评价函数用于粒子群中每个个体计算适应度。在文献［18］中，对任意输入，可采用下面的评价函数：

式中：C（u）为式（8）计算的航迹代价；BigM为一个比较大的数；C为约束违背量，采用式（19）计算如下：

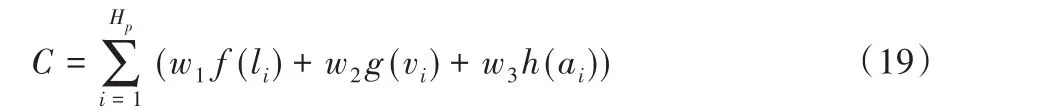
式中：f(li)表示航迹段穿越禁飞区的约束违背量；g(vi)和h(ai)表示速度和加速度的约束违背量；w1、w2、w3为权系数。

4.2.2 粒子群优化求解

根据第1章中相关工作的介绍，假设粒子群种群数为N，每个粒子的空间维数为D，第i个粒子的输入向量和速度为u i=(ui，1，ui，2，…，ui，D)，v i=(vi，1，vi，2，…，vi，D)。第i个粒子最优解 为P i=(pi，1，pi，2，…，pi，D)，粒 子 群 最 优 解 为G=(g1，g2，…，gD)。根据粒子群优化策略，按照式（1）、（2）、（3）更新粒子。在本文中，式（3）中的ωmax不再是一成不变的，而是根据粒子的适应值来更新，如果粒子是可行解，则按照ωk更新，如果粒子是不可行解，则按照式（20）更新：

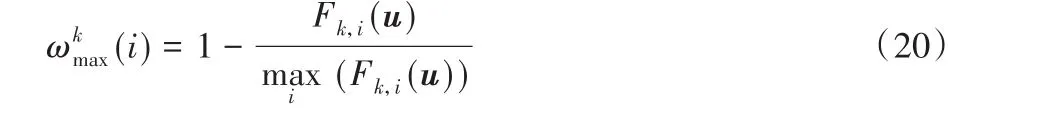
式中，Fk，i(u)为第k次迭代第i个粒子的适应度。基于ωmax改进的快速粒子群优化（FPSO）算法与经典粒子群优化算法相比，优化速度表现出明显的提升。

4.2.3 粒子群优化算法流程

根据上述描述，以下部分给出了粒子群优化算法的基本流程。

初始化粒子群P，包括粒子的位置和速度，全局最优值以及局部最优值

4.2.4 ADMPC滚动优化

在每一个采样时刻，MPC通过求解一个有限时域的优化问题，得到系统当前时刻的最优控制序列，从而实现在整个控制时域内系统的在线闭环控制。多无人机协同航迹规划ADMPC滚动优化过程如图6所示。

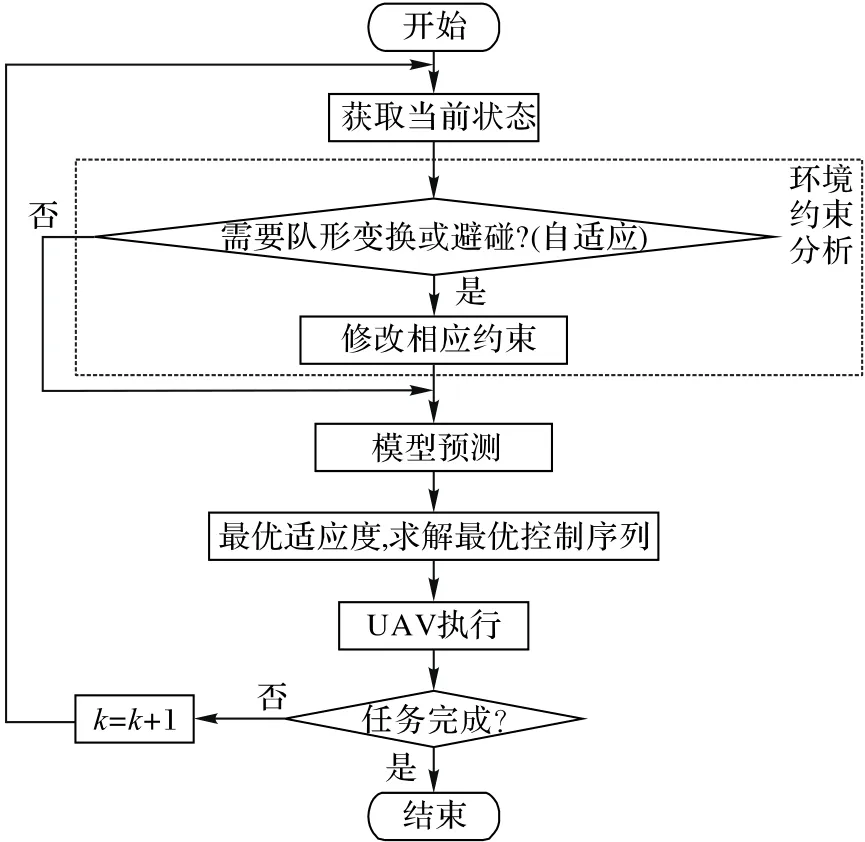
图6 多无人机协同航迹规划ADMPC滚动优化过程Fig.6 Flowchart of multi-UAV cooperativetrajectory planning ADMPCrolling optimization

其中，根据环境约束及自身状态，多无人机编队采取必要的队形变换或避障等动作。通过ADMPC方法对无人机状态进行预测，得到滚动在线优化问题，通过4.2.3节中提到的FPSO算法对其进行优化求解，计算其最优适应度，得到最优控制序列并执行，完成整个自适应编队控制任务过程。

4.3 多无人机协同航迹规划流程

步骤1 首先初始化无人机参数，设置最大速度、最大加速度等限制，设置模型预测控制参数，参数设置如表1所示。

步骤2 根据实时仿真环境，自适应选择多无人机编队宽度rf或队形，计算并更新虚拟编队引导点及与跟随无人机的对应关系，并根据式（15）建立各无人机间的通信关系。

步骤3 利用粒子群优化算法，分别对领航无人机和各跟随无人机进行航迹规划问题求解。

步骤4 取最优结果的第一个控制输入模型中，即代入式（5），计算无人机下一时刻的状态。

步骤5 如果到达目标点，完成协同航迹规划，任务结束；否则转步骤2。

5 仿真实验分析

为了验证方法的有效性，本文在Matlab 2016环境下进行了仿真实验。仿真实验将空间的障碍抽象为大小不一的矩形。领航无人机的预定起始位置为（25，0），目标位置为（-28，-6）。

多旋翼无人机其动力学可以由具有速度和加速度约束的质点动力学模型近似：

实验主要针对三架无人机在不同编队形式下的协同航迹规划，包括线性、三角、线性-三角编队（二者可根据环境情况相互变换），同时对三种编队形式下的飞行总航程进行了对比。另外，对九架无人机也做了简单的仿真实验，进一步展示了文中方法的灵活性和可扩展性。

表1为仿真实验参数，包括模型预测控制、多旋翼无人机基本参数、粒子群以及约束等基础参数。

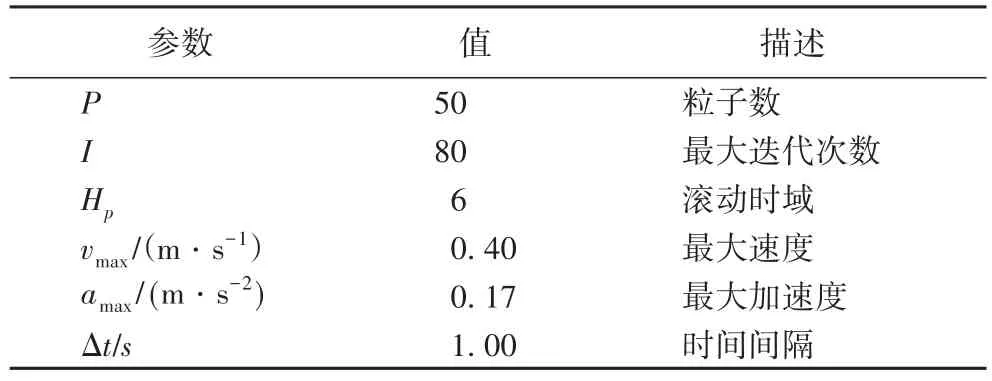
表1 仿真实验参数Tab.1 Simulation experiment parameters

实验一 三架无人机编队飞行。

图7展示了三架无人机协同航迹规划的预测过程，每次预测未来6个航迹点，并将第1个控制输入作为实际的输入值，剩下的预测航迹点作为参考航迹点。在此实验中，跟随无人机的初始位置分别为P1（26，0）和P2（27，0）。

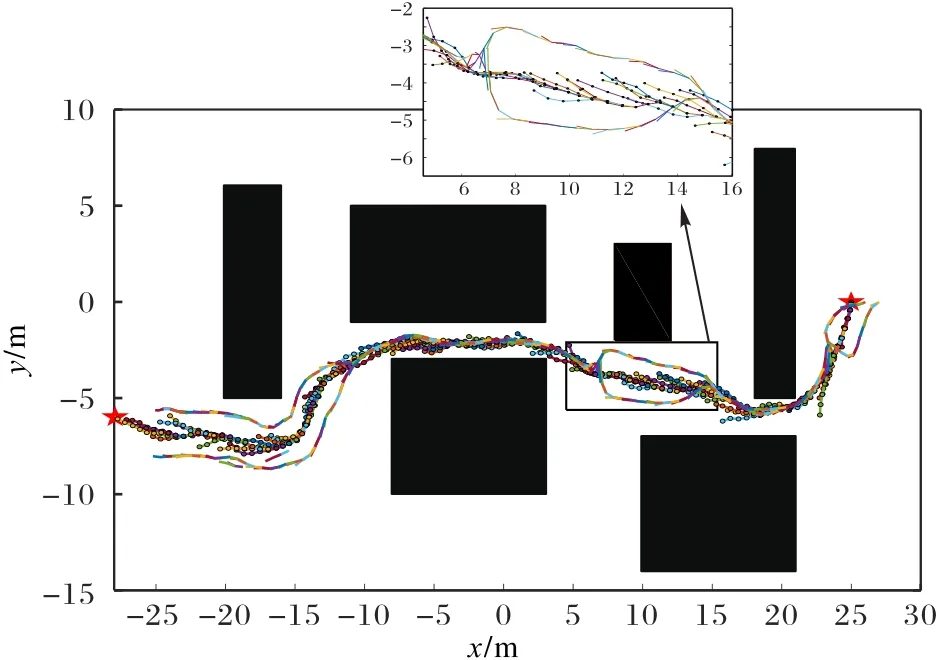
图7 多无人机协同航迹规划预测示意图（三架无人机）Fig.7 Prediction of multi-UAV cooperative trajectory planning（three UAVs）

如图8所示，实线为将每次预测值的第1个控制输入作为实际输入后规划的领航无人机完整航迹，6个虚线框则分别展示了不同环境下三架无人机的编队情况。在经过狭窄区域时，多无人机以线性编队飞行，而在经过空旷区域时，则以三角编队飞行。可以看出，在满足所有约束条件的前提下，规划出一条能保证多无人机编队安全穿过障碍区的实际可飞航迹。

实验二 线性、三角、线性-三角编队航迹规划对比。

图9展示了线性、三角、线性-三角三种编队形式下的飞行航迹对比情况。线性编队在编队航迹规划中，可简单地看作单个无人机并需满足其相应约束条件；而三角编队必须考虑编队宽度的约束；线性-三角编队表示整个编队根据不同环境进行相应队形转换，使得规划出的航迹在保证较低代价的同时，还满足假设2的要求。

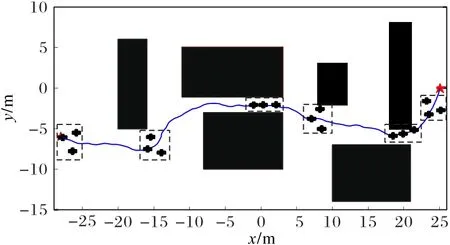
图8 多无人机协同飞行过程Fig.8 Processof multi-UAV cooperativeflight

图9 基于不同编队形式的航迹规划对比Fig.9 Trajectory planningcomparison of different formations

表2展示了在三种不同编队形式下，三架无人机飞行的航程对比情况，可以看出，在以航程为代价的航迹规划算法中，线性-三角编队在三种编队形式里，航迹规划最优，这也充分说明了本文所提出方法的优势所在。

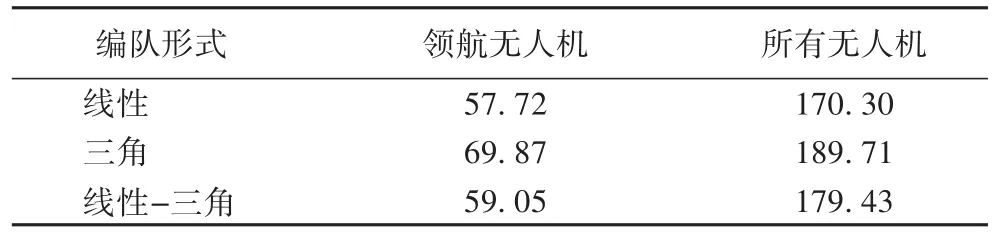
表2 不同编队形式航程比较 单位：mTab.2 Flight distancecomparison of different formations unit：m

实验三 基于人工势场法（APF）的编队协同控制方案［3］与本文编队协同控制方案的对比。

图10是利用APF进行多无人机编队协同控制的飞行效果，实线为虚拟领航无人机飞行航迹（航迹规划算法与本文一致），4个虚线框展示了4个代表性阶段的无人机编队飞行情况，实线上的圆点为虚拟领航无人机在各阶段的对应位置。可以看出，相较于本文的方案（如图8），基于APF的方案，无人机在一定程度上保持了编队飞行，但很难形成稳定的编队队形，且难以预测任一无人机的飞行情况。

图11进一步展示了利用本文方案，在整个规划过程中，其单步时间及平均时间都少于基于APF的编队控制方案。APF平均时间为0.0918 s，本文方案平均时间为0.0609 s。

实验四 无人机集群（九架）编队协同航迹规划。

无人机集群与三架无人机略有不同，其编队控制必须考虑通信距离与通信拓扑关系。在本实验中，增加的无人机以前三架无人机为参考，依据编队情况，确定相互之间对应的位置关系以及飞行次序，从而建立合理的通信连接，以保证实时信息交换，并形成稳定的编队队形。

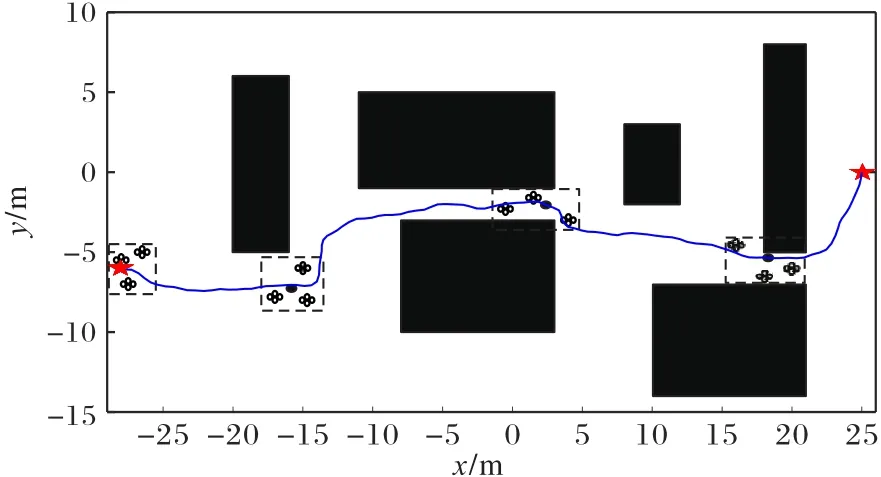
图10 基于人工势场法实现编队协同控制效果Fig.10 Effect of formation cooperativecontrol based on artificial potential field method

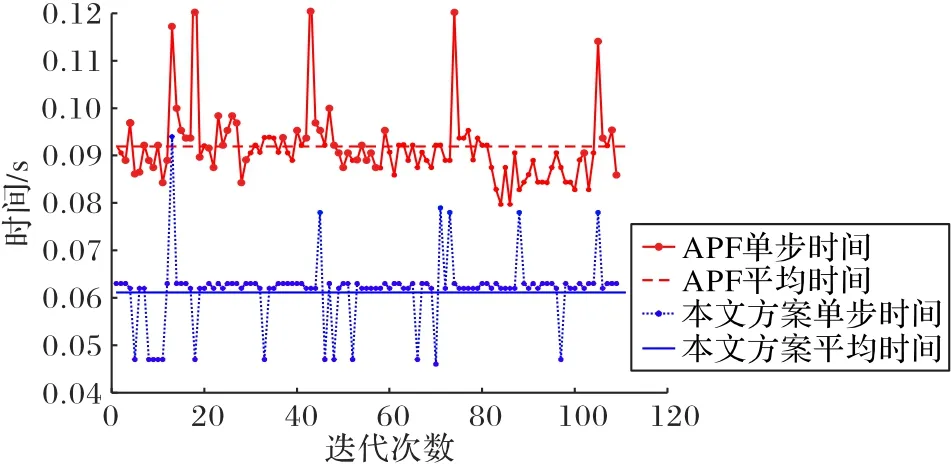
图11 协同航迹规划方案时间对比Fig.11 Timecomparison of cooperativetrajectory planningschemes

图12展示了无人机集群（九架）自适应编队协同飞行过程图，实线表示领航无人机飞行轨迹，两个虚线框展示了两个代表性阶段的无人机协同编队飞行情况。可以看出，在狭窄区域多无人机以线性编队飞行，在宽阔区域则以形呈特定编队飞行。通过此实验进一步验证了本文方法，有效解决了多无人机数量限制、通信拓扑结构约束等方面的难题。

6 结语

本文设计的基于自适应分布式模型预测控制的多无人机协同航迹规划方案，采用模型预测控制思想，将整个控制过程转化为基于滚动时域的在线优化问题；结合分布式策略，有效解决了多无人机在计算资源与通信链路等方面的约束限制问题，以及各无人机独立避障的问题。采用虚拟结构法与领航跟随法结合的策略，提出了虚拟编队引导点，对多无人机进行自适应编队控制，同时通过改进的粒子群优化算法对整个控制过程进行处理。仿真结果表明，利用本文提出的方案，有效解决了多无人机协同航迹规划问题，同时在编队队形的保持与变换控制中也表现出较好的效果；另外，该方案的应用还极大地增加了多无人机控制的灵活性，并降低了整个控制过程中的代价总和。在今后的工作中，可以把该方案扩展到三维环境下的无人机集群自适应编队协同航迹规划问题，并进一步提高求解算法的效率。