基于新的森林优化算法的特征选择算法

谢 琪，徐 旭，程耕国，陈和平

（1.武汉科技大学信息科学与工程学院，武汉430081； 2.格勒诺布尔高等商学院高等商业学院，格勒诺布尔38000，法国）

（∗通信作者电子邮箱85169023@qq.com）

0 引言

特征选择是机器学习和数据挖掘领域研究的热点之一［1］。特征选择是从一组特征中挑选出一些最有效的特征以降低特征空间维数的过程［2-3］。特征选择在数据预处理的过程中会去除冗余和无关的特征，能减轻维度灾难所产生的问题，同时能降低学习任务的难度，提升学习效果［4-5］。在分类问题中，特征选择能提高分类的准确性，能生成更快和更有效的分类器，能更好地了解关键特征的信息［6］。特征选择已被许多学者证明是有效的［7-9］。因此，特征选择是机器学习过程的重要组成部分，可以为之后的学习任务保留有用的特征，同时忽略不相关和不重要的特征［10］。

在2016年，Ghaemi等［11］提出基于森林优化算法的特征选择（Feature Selection using Forest Optimization Algorithm，FSFOA）算法［12］，该算法将森林优化算法（Forest Optimization Algorithm，FOA）用于特征选择。FSFOA与基于混合遗传算法的特征选择（Hybrid Genetic Algorithm for Feature Selection，HGAFS）算 法［13］、基 于 粒 子 群 优 化（Particle Swarm Optimization，PSO）算法的特征选择算法［14］和基于支持向量机的 特 征 选 择 算 法［15］（a novel Support Vector Machine based feature selection method using a fuzzy Complementary criterion，SVM-FuzCoc）等算法相比取得了不错的效果。FSFOA算法能提高特征学习的准确率，有效地除去冗余特征，并且还具备全局搜索能力。但是FSFOA算法存在一些不足：第一，FSFOA算法初始特征采用随机生成策略，随机初始化策略在非凸函数中可能会陷入局部最优，无法搜索到全局最优；第二，FSFOA算法远处播种使用的是候选森林中的树木，候选森林会产生优劣树不完备问题，影响到全局搜索；第三，实验发现，在最优树更新阶段会有相同适应度但是特征不同的树木，FSFOA算法会将这些树木淘汰，但是淘汰树木中存在维度更小或者能产生更高精度的树木。针对以上的问题，本文提出了基于一种新的森林优化算法的特征选择（New Feature Selection Using Forest Optimization Algorithm，NFSFOA）算法，该算法分别从森林的初始化、候选森林的生成和森林的更新3个方面作了改进。最后将新算法与传统算法在相同的测试数据下进行对比实验，实验结果表明，新的算法表现出了更准确的分类性能，并且能更有效地缩减维度。

1 特征选择综述

在机器学习和模式识别领域中，特征选择的好坏会直接影响分类器的性能，因此特征选择的方法非常重要。Dash等［16］提出了特征选择的框架。特征选择共分为4个部分：特征子集的搜索机制、特征子集的评价机制、停止准则和验证方法［17-18］。当前主要研究集中在搜索机制和评价机制。

根据特征子集评价机制的不同，可将特征选择方法分为三 类 ：过 滤 式（Filter）、包 裹 式（Wrapper）和 嵌 入 式（Embeding）［4］。过滤式方法［10，19］是先对数据进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关。过滤式特征选择方法一般使用评价函数来增加特征与类别之间的相关性，削减特征之间的相关性［1，16］。典型的过滤式特征选择是Relief。Kira等［20］提出 Relief方法是一种特征权重法，计算每个特征和类别之间的相关性，选择相关性大于一定阈值的特征作为特征子集或者指定要选择的特征个数K，然后选择相关性最大的K个特征作为特征子集。Relief方法只能处理二分类问题不能处理多分类问题。Kononenko［21］提出Relief-F方法，该方法用于处理多分类问题。过滤式方法的关键是选取评价函数，评价函数可分为四类：距离度量、信息度量、依赖性度量和一致性度量［16］。包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价准则［4］。典型的包裹式特征选择是拉斯维加斯包裹式特征选择（Las Vegas Wrapper，LVW）。Liu等［22］提出LVW方法在拉斯维加斯方法框架下，使用随机策略来进行子集搜索，并以最终分类器的误差作为特征子集的评价标准［4］。学者们使用不同机器学习算法用于包裹式特征选择，如决策树算法［23］、遗传算法（Genetic Algorithm，GA）［24］和 支 持 向 量 机（Support Vector Machine，SVM）［25］等。嵌入式特征选择是将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，即在学习器训练过程中自动地进行了特征选择［4］。正则化是典型的嵌入式特征的方法。Tikhonov等［26］提出岭回归算法在平方误差损失函数中引入L2范数正则化。Tibshirani等［27］提出套索算法（Least Absolute Shrinkage and Selection Operator，LASSO），与岭回归算法类似该算法使用平方误差函数作为损失函数，区别在于该算法使用范数正则化替代L2范数正则化。使用正则化求解得到的非零权重对应的特征就是最终求解的特征。正则化将特征选择和学习器训练同时完成，学习器训练完成则特征选择完成。

进化算法是通过模拟自然界生物不断进化的过程以实现随机搜索的一类算法［28］。进化算法具有高鲁棒性和自适应性，能有效处理传统优化算法难以解决的复杂问题，可用于求解全局最优解问题［29］。基于进化算法具备的上述优点，学者们使用进化算法用于特征选择［5］。遗传算法是进化算法的一种，Yang等［30］提出使用遗传算法进行特征选择。Dong等［31］提出一种颗粒信息与遗传算法相结合的特征算法，该方法使用改进的特征粒度遗传算法用于特征选择。Dorigo等［32-33］提出蚁群算法（Ant Colony Optimization，ACO），该算法是启发式算法，并用于求解组合优化问题。Kabir等［34］提出一种混合蚁群优化算法用于特征选择，该算法结合了过滤式特征选择和包裹式特征选择的优点。Wan等［35］提出一种改进的二进制编码蚁群算法用于特征选择，该算法使用遗传算法初始化蚁群算法的信息素的初始信息。Kenned等［36-37］提出粒子群优化（PSO）算法，该算法利用个体信息共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程。Xue等［14］提出了分类问题中基于粒子群算法的特征选择算法，该算法提出了三种新的初始化策略和三种新的个体最佳和全局最佳的更新机制。Zhang等［38］提出基于裸骨粒子群算法，该算法设计了一种增强记忆策略来更新粒子的局部领导者，避免了粒子中优秀基因的退化。Tran等［39］总结了粒子群优化算法在特征选择中的运用。最近几年进化算法产生了一个新的分支，Ghaemi等［11］根据森林中树木优胜劣汰的生长过程提出了森林优化算法（Forest Optimization Algorithm，FOA）。森林优化算法是一种仿生类智能优化算法，它模拟森林中种子传播的过程进行搜索最优解，用于解决非线性连续型优化问题［40］。

2 基于森林优化算法的特征选择

FSFOA算法共分为5个步骤：初始化森林（Initialize Trees）、本地播种（Local Seeding）、规模限制（Population Limiting）、远处播种（Global Seeding）和更新最优树（Update the Best Tree）。

步骤1 初始化森林。随机产生一些树木初始化生成一个森林，每棵树木由特征值、树龄（Age）和适应度（Fitness）值组成。特征值是一个随机产生的“0”或“1”的一维向量，“0”代表了对应的特征被删除，“1”代表了对应的特征被选择。Age设置为0。适应度是评价这棵树选择的特征在数据集上的学习能力，FSFOA算法使用的适应度函数为：邻近算法（K-Nearest Neighbor，KNN）［41］、支持向量机算法［42］和C4.5算法［43］。

步骤2 本地播种。在本地播种阶段，将森林中树龄为0的树参与本地播种，其余树木不参与本地播种。将树龄为0的树依据参数本地播种变换（Local Seeding Change，LSC）值复制生成若干个相同特征值的树木。每棵新生成的树特征值随机选择一位取反，如果值为“0”则变成“1”，反之亦然。最后森林中所有树木的Age值加1，新树Age值置0，并将新树加入森林之中。本地播种的过程用于算法的局部搜索。

步骤3 规模限制。FSFOA算法把控制树木数量的过程称为规模限制（Population Limiting）。规模限制的方式有两种：第一种，将树龄大于年龄上限（Life Time）值的树木淘汰，这种方式模拟树木正常死亡的过程；第二种，在淘汰掉树龄大于“Life Time”值的树木之后，森林数量的规模如果还大于规模上限（Area Limit）值，将所有树木的适应度（Fitness）做降序排列，淘汰掉适应度小的树木，将森林的规模控制在“Area Limit”值以内，这种方式模拟自然界适者生存法则。

步骤4 远处播种。FSFOA算法通过模拟远处播种的过程为算法提供全局搜索方法。算法依据转移率（Transfer Rate）的值随机选择候选森林中一定比例的树木用于远处播种。每棵远处播种的树木依据远处播种变化（Global Seeding Change，GSC）值随机选择若干个特征值取反。

步骤5 更新最优树。在更新最优树阶段，选择森林中适应度最大的树，将这些树的年龄值置为0，重新放入森林中。

3 基于改进的森林优化算法的特征选择

3.1 FSFOA算法的不足

FSFOA算法在以下3个方面存在不足：

1）FSFOA算法在初始化森林阶段，初始化的树木采用完全随机方式，完全随机策略在非凸函数问题中容易陷入局部最优解。

2）FSFOA算法在规模限制阶段通过两种策略限制森林的规模，并将淘汰的树木生成候选森林，并按一定比例数量用于远处播种。这种会产生“优劣”树不完备问题，影响全局搜索。

规模限制的第一种方式是模拟优质树的自然死亡，将树龄达到“Life Time”值淘汰进入候选森林，树龄能达到“Life Time”值的树以前没有被淘汰说明这类树的fitness会大于一般的树，否则之前就会被淘汰，这样的树是一种“优质树”。规模限制的第二种方式是如果森林的规模超过了“Area Limit”值，淘汰fitness最小的树。这种方式是模拟森林中优胜劣汰的过程，有的树由于基因或者环境的问题还没有长大就死亡了，说明这种树是一种“劣质树”。将优质树和劣质树混在一起形成候选森林，按一定比例进行远处播种，由于优质树和劣质树混在一起选择，有可能选择到的都是优质树或者都是劣质树，最终影响到全局搜索。

3）在最优树更新阶段会有相同适应度但是特征不同的树木，FSFOA算法是将这些树木淘汰，但是淘汰树木中存在维度更小或者能产生更高精度的树木。

3.2 FSFOA算法的改进

针对FSFOA算法以上的不足，本文相应提出了3点改进：

1）初始化策略的改进。初始化策略共分为两步：第一步，计算数据所有特征与标签之间的皮尔森相关系数，取相关系数为正的特征作为备选特征集；第二步，将备选特征集使用L1正则化特征选择法选出权重为非0的特征。

通过使用皮尔森相关系数和L1正则化两次选择之后产生的特征集合与标签之间具有很高的关联性。与随机初始化策略相比，新的初始化策略选择的特征集合能够快速地收敛到极值，并有助于搜索到最优的特征子集。

皮尔森相关系数（Pearson Correlation Coefficient）也称皮尔森积矩相关系数（Pearson Product-moment Correlation Coefficient），是一种线性相关系数。皮尔森相关系数是用来反映两个变量线性相关程度的统计量。相关系数描述的是两个变量间线性相关强弱的程度，相关系数的绝对值越大表明相关性越强。皮尔森相关系数等于两个向量的协方差除以各自的标准差，如式（1）所示：其中：Cov(X，Y)代表向量X和向量Y的协方差，σx代表向量X的标准差，σy代表向量Y的标准差，E代表期望，ρxy代表向量X和向量Y的皮尔森相关系数。

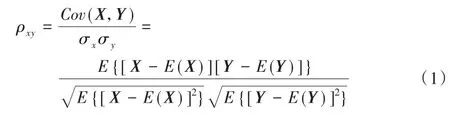
皮尔森相关系数的取值范围在-1到1之间：相关系数为0，说明两个向量不是线性相关；如果相关系数大于0，说明两个向量正相关；如果相关系数小于0，说明两个向量负相关。皮尔森相关系数特征选择法是过滤式特征选择的一种。

2）候选森林的改进。根据规模限制的两个策略将候选森林分为“优质森林”和“劣质森林”，将“优质森林”和“劣质森林”分别按“Transfer Rate”的值随机选择树木进行远处播种。由于规模限制的策略不同，“优质森林”和“劣质森林”会产生“类别不平衡”问题，即“优质森林”的数量会远大于“劣质森林”的数量或者相反。为了解决“类别不平衡”问题，当“优质森林”数量大于“劣质森林”数量时，在森林中选择fitness最小的若干个树木补足“优质森林”和“劣质森林”之间数量的差额；反之则在森林中选择fitness最大的若干个树木补足差额。

3）最优树更新和选择的改进。在FSFOA算法中，当远处播种生成的新树的最大fitness与森林中最大fitness相同时，新树被淘汰。在新的更新机制中，如果新树的最大fitness等于森林中最大的fitness时，则将这些新树Age置0后添加到森林中。这是因为当新树和旧树fitness相同时，存在维度更小的新树，因此将新树添加到森林之中有利于维度的缩小；如果fitness相同但新树的维度大于等于旧树，将这样的新树也添加到森林中，因为这样的新树再通过传播存在产生性能更好的树，以提高了搜索全局最优解的可能。最后，在最优树选择阶段，选择fitness最大的树，如果有多个fitness最大的树则选择特征数量最少的树。

3.3 算法的流程

改进算法的流程如图1所示。

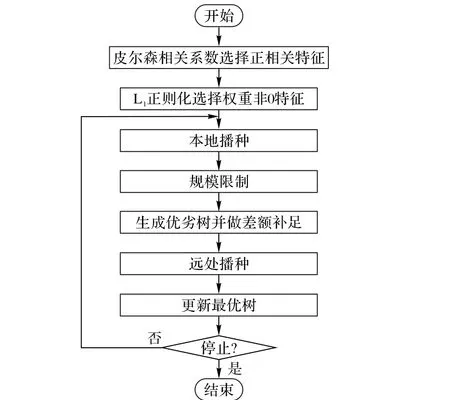
图1 NFSFOA算法流程Fig.1 Flowchart of NFSFOA algorithm

4 实验

为了证明新算法的有效性，实验采用与FSFOA算法相同的数据集和参数，实验从UCI机器学习库［44］中获得10个数据集。实验程序用python3编写，使用scikit-learn工具包编写L1嵌入式特征选择、皮尔森相关系数过滤式特征选择以及其他机器学习的算法。所有实验都在MacBook Pro 3.5 GHz Intel Core i7处理器下执行。

4.1 实验数据

实验数据一共包含了10个数据集合，分别是：Wine、Ionosphere、Vehicle、Glass、Segmentation、SRBCT、Heart-statlog、Cleveland、Sonar和Dermatology。FSFOA算法将实验数据集根据特征数量的个数分为“小维度”“中维度”和“大维度”数据集，分别对应的特征数量的范围是［0，19］、［20，49］、［50，∞］［12］。根据以上划分的依据，数据集中包含6个小维数据集、2个中维数据集和2个大维数据集。实验数据集合的相关说明如表1所示。

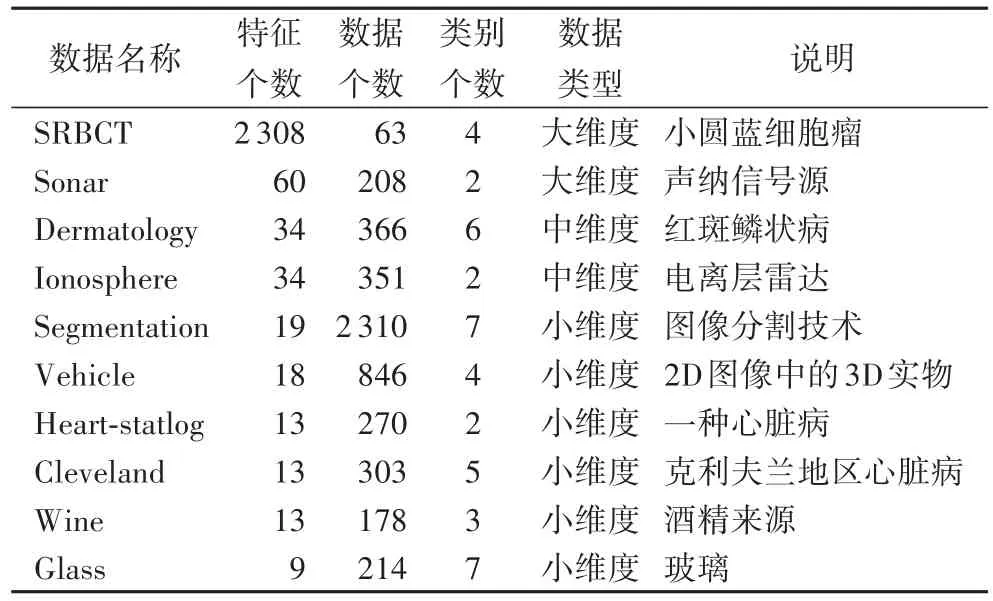
表1 实验数据集说明表Tab.1 Descriptions of experimental data

4.2 实验参数

新算法的参数与FSFOA算法的参数一致，FSFOA算法共有5个参数：树的年龄上限（Life Time）、树的规模上限（Area Limit）、远处播种的比例（Transfer Rate）、本地播种变化个数（LSC）和远处播种变化个数（GSC）。FOA指出参数“Life Time”“Area Limit”和“Transfer Rate”与数据集的数量无关［11］。FSFOA算法将这3个参数设定为固定值，“Life Time”为15、“Area Limit”为 50、“Transfer Rate”为5%［12］。FOA指出LSC 和GSC与特征的个数相关［11］。FSFOA算法设定了10个数据集的LSC和GSC值，如表2所示。

表2 实验数据集参数表Tab.2 Parametersof experimental data

为了防止产生过拟合问题，通常会将实验数据分为训练集、验证集和测试集，使用验证集来减少过拟合问题的产生。由于本次实验的数据较少，如果增加验证集，训练集较少将会产生欠拟合。因此实验不使用验证集，而使用10折交叉验证、2折交叉验证和70%训练集与30%测试集。10折交叉验证是指将数据集合分为10份，其中9份作为训练集，1份作为测试集，重复10次每次使用的测试集不同，最后将10次测试结果求均值。

评价算法的性能使用两个函数：分类精确性（Classification Accuracy，CA）和 维 度 减 少 率（Dimension Reduction，DR），CA和DR如式（2）和式（3）所示：

其中：N_CC是测试数据中分类正确的数据个数，N_AC是测试数据的总数。

其中：N_SF是通过算法选择到的特征个数，N_AF是特征的总数。

CA和DR的值域为［0，1］。CA是分类算法的准确性，CA值越大说明该算法分类性能越好；DR是特征选择算法特征维度选择能力，DR值越大说明算法维度缩减能力越强。

适应度函数使用KNN、C4.5、SVM，参数如表3所示。

表3 适应度函数和参数Tab.3 Fitness functions and parameters

4.3 实验结果

如表4所示，NFSFOA算法和FSFOA算法在不同数据集、不同适应度函数和不同验证方式下的实验结果。通过表4可以发现，在数据集Sonar、Dermatology、Ionosphere、Segmentation和Vehicle中，NFSFOA算法的测试精度和维度缩减能力相较于FSFOA算法在相同测试条件下都有提高。在SRBCT数据集中，NFSFOA算法和FSFOA算法测试精度相同，NFSFOA算法维度缩减能力提高。在Heart-statlog和Wine数据集中，NFSFOA算法在部分条件下测试精度有提高，维度缩减能力全部有提高。在Cleveland和Glass数据集中，测试精度都有提高，部分条件下维度缩减能力下降。

4.4 实验结果分析

第一，在SRBCT数据集中，NFSFOA算法和FSFOA算法测试精度相同是因为SRBCT数据集特征个数为2 308但数据只有63条，特征个数远大于数据个数，这样的数据集容易陷入过拟合。SRBCT数据集采用70%训练30%测试的方式，一共测试数据19条，94.73%的测试准确率，19条数据中18条数据分类正确，只有1条分类错误。94.73%的测试准确率达到了分类器的极限，如果精确率再提高则分类正确率达到100%。

第二，在Heart-statlog和Wine数据集中，在部分情况下分类精度有下降。在Cleveland和Glass数据集中，在部分情况下维度缩减能力有下降。主要原因是与其他数据集相比，Heart-statlog、Wine、Cleveland和Glass这四个数据集的特征维度最小，分别是13个特征和9个特征。说明NFSFOA算法在维度太小的数据集上分类性能和维度缩减能力有限。

第 三 ，在 数 据 集 Sonar、Dermatology、Ionosphere、Segmentation和Vehicle中，NFSFOA算法分类性能和维度缩减能力都有提高。说明NFSFOA算法在中大维度的数据集中有不错的性能。

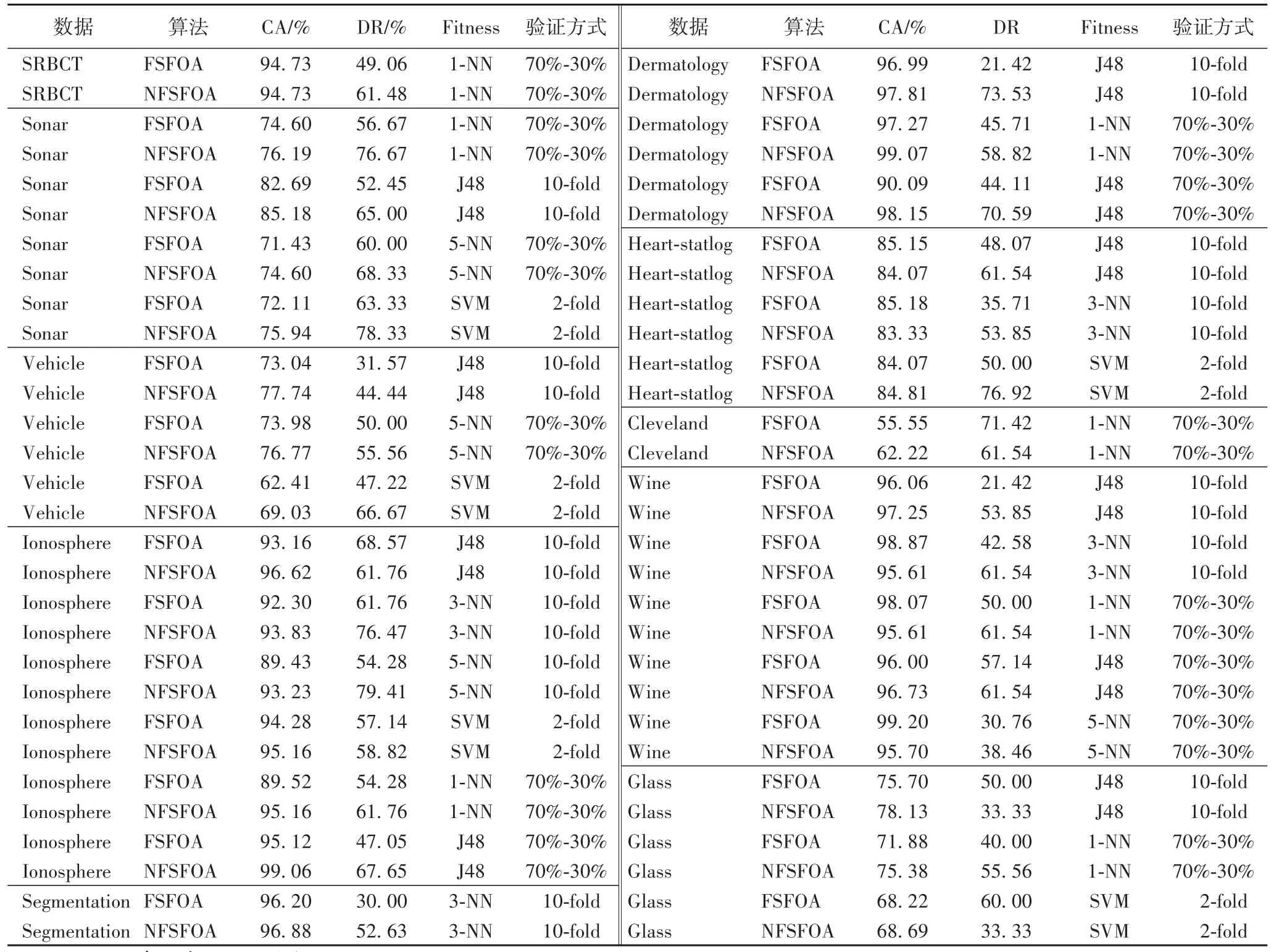
表4 NFSFOA算法和FSFOA算法在不同数据上性能的对比Tab.4 Performancecomparison between NFSFOA algorithmand FSFOA algorithmon different data

5 结语

本文针对FSFOA算法存在的三个问题，提出了一种基于改进的森林优化算法的特征选择算法。该算法提出了三个方面的改进：第一，在初始化阶段使用皮尔森相关系数和L1正则化代替随机初始化；第二，在候选森林生成阶段将优质树和劣质树分开采用差额补足的方法解决优劣树不平衡问题；第三，在更新解决段将精度相同但维度不同的树添加到森林中。本文通过实验，测试了小维度、中维度和大维度的数据集，新算法在中大维度数据上分类性能和维度缩减能力均有提高。