求解旅行商问题的多尺度量子自由粒子优化算法

杨云亭，王 鹏

（1.中国科学院成都计算机应用研究所，成都610041； 2.中国科学院大学，北京100049；3.西南民族大学计算机科学与技术学院，成都610225）

（∗通信作者电子邮箱wp002005@163.com）

0 引言

近些年来，元启发式优化算法［1］发展迅猛，不断地被挖掘应用到现实中的大规模问题中，如神经网络模型及参数优化、强化学习中的策略选择等热门技术中，相比传统算法中的精确算法中的动态规划、分支限定等，更加灵活和通用。元启发式优化算法求解优化问题的过程中，不受限于目标函数的可导性质和优化问题的对偶规则，就可以对问题进行算法的求解，同时可以在非常大的候选解空间中进行迭代搜索［2］。在通用的启发式优化算法中，模拟退火（Simulate Anneal，SA）算法［3-5］将优化问题看作是物理退火的过程，根据Metropolis准则选择是否接受搜索到的新解，直至退火过程结束；遗传算法（Genetic Algorithm，GA）［6-8］在当前搜索到解的基础上进行自然法则的变化：遗传、变异、交叉产生新解，在新解中应用“物竞天择，适者生存”法则进行最优解的替换；粒子群优化（Particle Swarm Optimization，PSO）算法［9］则根据鸟类的飞行规律进行解空间中的搜索，通过不同位置的速度和位移变化进行新解的搜索和替换。这些不同的搜索方式会使解沿着某种方向趋近于全局最优解，当搜索足够充分的情况下，这类启发式算法会以概率1收敛于全局最优。本文模拟量子体系下自由粒子的波函数的概率解释进行优化算法搜索行为的指导，提出了多尺度量子自由粒子优化算法（Multi-scale Free Particle Optimization Algorithm，MFPOA）。

组合优化问题是现实生活中很多问题的抽象，求解此类问题可以借助元启发式优化算法进行离散状态空间中的搜索。本文使用MFPOA对组合优化问题中的旅行商问题（Travelling Salesman Problem，TSP）［10-12］进行求解，首先对MFPOA进行了物理模型和基本流程进行了阐述，并采用了光骨头烟花算法（Bare Bones Fireworks Algorithm，BBFWA）［13］中的尺度迭代策略对算法进行了改进，将算法应用到TSP数据集上进行优化问题的求解。另外，通过与目前较优的启发式优化算法中的混合粒子群优化（Hybrid Particle Swarm Optimization，HPSO）算法［14］、模拟退火算法、遗传算法和蚁群优化（Ant Colony Optimization，ACO）算法［15］进行TSP求解能力的对比，进一步验证自由粒子模型下优化算法的性能。使用量子概率驱动解的搜索过程是一种创新的方式，同时完善的量子理论可以支撑算法的求解可行性。

1 基于量子概率的MFPOA

1.1 MFPOA的物理模型描述

多尺度量子谐振子优化算法（Multi-Scale Quantum Harmonic oscillator Optimization Algorithm，MQHOA）［16-18］是一种基于一维量子谐振子波函数原理提出的优化算法，模拟量子系统下的谐振子运动规律，将优化问题的求解通过量子谐振子过程和多尺度过程实现全局区域的逐步搜索定位和局部区域的充分搜索。在该算法的基础之上，对量子微观系统下的自由粒子的运动方式进行了分析，并将自由粒子的运动规律映射到函数优化过程中。物理学中的薛定谔方程可以通过给定的势阱函数求解出粒子的波函数，进一步通过波函数平方计算得到粒子在势阱下的概率密度函数。而复杂的势阱较难通过薛定谔方程求解出波函数，在此通过势阱函数的泰勒展开公式的近似求得近似波函数，在波函数的指导下进行可行解空间的采样搜索。在优化问题中将优化问题的目标函数近似薛定谔方程中的势阱，采用势阱函数的零阶泰勒公式近似，可以得到简洁的势阱表达，然后通过薛定谔方程求解出近似波函数形式。借助物理学中波函数的概率意义，指导优化算法在空间中进行采样。

多尺度量子自由粒子优化算法是从微观系统中的自由粒子衍生出来，自由粒子是量子系统下简单的粒子之一，在空间中不受力的作用，并且没有能级结构，转化到优化求解过程中，可以实现简洁的搜索结构。目标函数的零阶泰勒展开式为常数，在薛定谔方程中使用0表示势阱，这与自由粒子在空间中不受力等效。首先将自由粒子的势阱0带到薛定谔方程中得到波函数的表达，然后通过波函数的平方表征粒子在空间中出现的概率，该概率形式指导算法在当前搜索的最优解和当前的搜索尺度下依此概率进行迭代搜索。将量子空间中简单的粒子形式映射到优化算法中，通过均匀分布采样和尺度收缩在求解过程中实现当前最优解的替换，当搜索足够多次后实现最优解的收敛。

量子理论中的不受力的自由粒子的薛定谔方程写作如下形式：

其中：ℏ为普朗克常数，m为粒子的质量，ψ(x)为粒子的波函数，E为粒子的能量。

通过方程求解的波函数如下所示。

粒子在空间中的存在是不确定的，但是可以通过波函数模的平方表示粒子在空间某位置上的概率，如式（3）：

式（3）可以看出自由粒子的波函数的概率意义表示粒子在空间中任何位置存在的概率是一个常数，也即在空间任何位置中存在的概率相同，在算法求解过程中可以使用均匀分布进行近似。MFPOA模拟粒子的运动过程，采用均匀分布在可行域中进行采样，根据采样点在优化函数中的函数值的信息选取下次迭代过程中的采样中心，并根据多次采样信息决定尺度的收缩，直到搜索过程中达到结束条件，退出迭代。

1.2 MFPOA的基本工作流程

MFPOA在算法搜索过程中是逐渐减小搜索区域的，直至搜索区域减小到给定搜索区域的最小值，说明算法求解已经收敛到接近全局最优的程度，算法结束。算法基于概率的形式进行采样，在某一个尺度是否达到充分的搜索只能通过一些预设条件的判断，但是这种判断一般都是存在一定误差，在判定充分搜索后可能还存在跳过的区域。基于这种判断的误差性，本节介绍了一种自适应的尺度变化策略，这种策略不同于预先设定迭代充分搜索的次数，而是使用搜索过程中的信息进行尺度的持续自适应变化。模拟量子自由粒子在空间中的存在概率，MFPOA通过概率采样在可行解空间中进行搜索，并实现优化问题的求解，其伪代码如下所示。

算法1 MFPOA。

算法初始化自由粒子的个数k，搜索空间的最小值min，最大值max，最后停止迭代的搜索空间的最小值δmin，初始的搜索区间在[min，max]，和充分搜索的判定条件c值，实验一般设定c值为10，f(x)表示目标函数。2）～3）行表示随机生成k个解空间中粒子，并计算每个粒子的在目标函数中的函数值，并记录其中最优解f(x)best；4）～12）行表示算法迭代搜索的过程，分别以k个粒子为中心进行均匀分布采样产生新的粒子，采样的尺度跟当前的δ有关。采样后的粒子在目标函数中表现更优的情况下进行粒子的替换，并将当前粒子中的最差用当前k个粒子中的最好粒子更新。若此次迭代过程中的最优值相较上次迭代过程中的最优值没有发生变化，则最优值的优越性系数为2，下次迭代若最优值依然不变，优越系数增加1，如此累计，直到优越系数等于c时，表示此搜索区域已搜索充分，搜索区域减半，进行更精细的搜索。否则，在当前尺度下进行最优值替换，进一步地迭代搜索，尺度不减小。

模拟自由粒子在空间中存在的概率分布的形式，MFPOA通过均匀分布采样，探索可行域中最优解的存在位置，不断地通过迭代进行中心替换和搜索尺度变化，逼近可行域中的最优解。这种方式是将最终解的形式看作是一种在特定区域的概率分布，而不再是一个特定的值。当无限次迭代后，可行解会慢慢逼近到一个极小的区域中，回到最终的值的形式。从伪代码中也可以看出，算法中控制搜索区域变化的参数c决定整个算法求解在当前搜索尺度下收敛的情况。c值设置得过小，在当前尺度下进行采样搜索不够充分，进行尺度减半会丢失大部分解空间，导致算法求解性能下降。c值设置得过大，会使算法在解空间中进行大量采样和最优值判断及替换，大幅增加算法求解的时间，而使算法求解速度不可忍受。c值的设定使算法增加了可调参数的设置，c值设置的不合理性会严重影响算法的收敛能力和求解精度，一般设置为10。

基于此，本文参考了2018年提出的BBFWA中搜索区域变化的策略。BBFWA在烟花算法的基础上简化了算法求解的结构，对烟花爆炸的半径距离进行了动态的调整来提高算法的求解效果。烟花算法模型同样采用了均匀分布的采样方式进行可行解的探索，不同的是MFPOA在搜索过程中通过判断当前尺度搜索的充分性进行尺度的缩小，而BBFWA在搜索过程中根据采样前后最优值的变化情况进行尺度的更新。这种尺度的自适应更新实质是对尺度持续衰减的一种改变，在每次采样完后进行在原尺度的更新，在最优值变得更优的情况下，下一次采样尺度在当前尺度上扩大至原来的1.2倍；否则，在当前尺度上缩小至原来的0.9倍。这种尺度的变化更加缓慢，相对于尺度减半策略不会丢失解空间中的大部分信息。

为了减少MFPOA中可调参数c值的影响和避免尺度减半导致的解空间的信息的丢失，采用了BBFWA中烟花爆炸半径的改变策略对算法的搜索尺度进行了一种改进，使用迭代过程中的信息指导尺度的减小，去掉c值的判定条件，采用量子自由粒子的概率解释在搜索空间中寻优的方式是一种新型搜索算法的框架。BBFWA实质上是对自由粒子模型下的算法进行了搜索尺度的改进，在MFPOA简单结构的基础上进一步地改进策略的指导，可以产生性能更优的算法，同样自由粒子算法可以对同样机理搜索的算法进行可行性的解释。光骨头烟花算法在自由粒子优化算法的解释下的伪代码可以进一步改写成如下形式，并记为MFPOA-DS（Multi-scale Free Particle Optimization Algorithm-Dynamic Search）。

从算法1和算法2中的两段伪代码中可以明显看出，MFPOA-DS版本中尺度的更新使用了公式δ=δ*λ，其中λ的取值有两种0.9和1.2：只有迭代中产生的新粒子比上一次迭代中的粒子的最优值好，设置λ=1.2，进行搜索区域的扩大；否则进行搜索区域的衰减。MFPOA减半的搜索方式使得算法搜索过程中会忽视搜索中心外围区域，过于关注内部区域，这种方式会导致可行解空间中的部分信息丢失，从而对优化问题的求解不准确。这种策略引入动态尺度搜索的概念，将前后两次搜索到的解的变化情况代替尺度收敛的控制条件值c的判断，可以使尺度灵活缩放，进而改善算法的性能。

2 自由粒子模型求解TSP的基本过程

TSP一直是组合优化问题中经典的NP难问题。TSP的描述是给定若干城市和城市之间的距离，通过算法求解访问每座城市并返回出发城市的最小回路距离，也称为最短路径问题。启发式优化算法往往更擅长连续空间中的优化问题，在求解组合优化问题时需要先对组合优化问题进行合适的映射，进而按照函数优化求解的思路进行求解。相比连续空间中的函数优化，组合优化问题需要先选择优化问题解的编码方式以及可行解的更新方式。TSP解的编码与给定的城市数目有关，路径距离基于城市序列计算欧几里得距离得出，所以城市序列的表示尤为重要，简单的一种表达方式是对城市进行编号，比如5个城市，分别给每个城市编成1，2，…，5。城市序列123451便表示TSP的一个可行解，表示从城市1出发，分别经过城市2，3，4，5，再回到城市1。在编码方式的基础之上，通过随机选择两个位置进行交换产生新解。

TSP作为离散问题求解的代表，一直是组合优化问题中经典问题。如何求解城市序列的最优路径，使得旅行商经过的总路程最小，也一直以来被用来测试启发式算法的性能。MFPOA求解TSP的策略主要包含两个步骤：1）在当前尺度下进行城市序列的迭代并记录最优解的情况和采样中心的变化；2）在不同尺度下进行城市序列在已搜索到最优区域的精细搜索。根据多尺度量子自由粒子模型，MFPOA-DS求解TSP的基本工作流程的伪代码如下所示：

由伪代码和算法的基本思想，可以将自由粒子模型求解TSP的基本过程概述为以下3个主要步骤：

1）随机初始化k个城市序列，2，…，k）作为当前尺度（初始尺度）下的搜索中心。

2）在当前尺度δ上的收敛过程，以每次迭代过程中保留的k个较好的采样位置作为k个局部搜索区域的中心，形成k个区间为δ的均匀分布函数U(xi-δ2，xi+δ2)。分别根据每个中心序列进行随机位置的交换产生新解，在迭代过程中记录最优解和最优解的位置，实现单一均匀分布的收敛，多个均匀分布采样迭代的过程实现当前尺度下的基本收敛。

3）搜索区域的聚焦过程，在上一尺度搜索下达到基本收敛的情况下，根据实际求解到的最优解的变化情况进行当前尺度的变化，实现局部区域的精细搜索，直到搜索区域减小到足够小或者得到预设定的迭代次数。

当给定n个城市的坐标时，可以通过欧几里得距离计算城市之间的距离。可行解空间表示为n个城市的全排列，一共有n！种方案，算法的求解便在这些方案中进行搜索求解。一一穷举这些解在城市数目很多的情况下是不可行的，启发式算法在求解过程中根据当前最优解的分布进行下一步的搜索，有选择地进行搜索区域的迭代来避免全部空间的穷尽搜索。在求解TSP时，算法中δ的初始值设为城市总数，δmin设置为1，在[1，δ]区间内进行均匀分布随机位置的产生，当δ小于1时没有意义。l(x)表示城市序列的路程长度，从一个城市出发，历经所有城市后回到原始出发的城市的路径长度。在MFPOA求解中δ随着迭代过程按照固定倍数进行减小，在MFPOA-DS中δ随着迭代过程中搜索到的解的情况进行自适应的尺度增减。这一尺度的变化控制着算法求解TSP的收敛情况，当尺度缩小到一定程度(δmin=1)，算法终止。

MFPOA本身模拟量子系统下的自由粒子的特点进行优化问题中的可行域的搜索，搜索策略简洁，通过均匀分布采样和最优值替换得到最终整体的最优解。同样在TSP中通过简单的城市序列变换在可变的搜索空间中进行最优解的搜索。当迭代足够充分，算法求解的最优城市序列会逼近最优解。

3 仿真实验与分析

本章使用组合优化问题中代表性的TSP测试自由粒子模型算法的性能。连续优化问题更容易针对不同的问题在合适的范围进行采样，组合优化问题需要先进行合适的映射，将问题中的求解结果用合适的序列表示，同时采样过程需要根据问题制定。使用自由粒子优化算法求解TSP时，将问题映射成一个在初始解的基础上进行交换位置的均匀分布采样产生新解，根据新解比当前解的效果进行采样尺度的变化（采样尺度初始为城市序列中的城市个数）。在MFPOA中的尺度变化根据迭代过程中的解不发生变化的次数进行尺度的减半策略。在尺度自适应改变版本MFPOA-DS的算法中，根据搜索中的解的变化进行采样尺度的放缩变化，相比原始做法，降低了算法的复杂度，使算法更加灵活。

所有仿真实验均在Intel Xeon CPU E5-1630 v3 3.7 GHz，16 GB内存的计算机上进行，程序采用Matlab 2018a实现。经过反复实验测试，在本次TSP上测试过程中使用参数设置如下，初始粒子个数k为30，初始的搜索尺度δ为求解TSP时的城市数目，算法停止迭代的条件δmin设置为1，最大迭代次数w0设置为30 000，搜索尺度变化系数λ初始为1，在迭代过程中随最优解的变化在1.2和0.9之间变化。城市间的距离采用欧几里得距离进行度量。

3.1 尺度自适应变换策略的有效性

实验采用不同的对称性TSP的数据验证算法求解的可行性。实验采用了 ulysses16、ulysses22、eli51、burma14、bayg29的实验数据，通过这些数据测试了MQHOA和使用尺度自适应改进策略的MQHOA（MQHOA-DS）、MFPOA和MFPOA-DS。由于算法的随机性，采用了10次重复实验数据进行对比，实验数据如表1。

表1 10次重复实验在不同实验数据上的结果对比Tab.1 Result comparison of 10 repeated experiments on different experimental data

MFPOA在MQHOA的启发下，考察了量子系统中的不同粒子在微观系统下的运动形式对算法指导优化求解过程的影响，主要考察了10次独立重复实验的最优值（Global Best，GB），10次实验结果的平均值（Mean Best，MB）和10次实验结果的平均值与最优值间的差距（MB-GB）。对比MFPOA和MFPOA-DS，MFPOA-DS在5种数据集上性能比MFPOA都有相应的提升。根据迭代过程中得到的解的情况进行尺度的缩减和放大，可以有效提高算法的搜索能力。而且通过观察重复实验中最好值和平均值的差距，可以发现使用自适应尺度变化策略后的算法会减弱算法每次运行的随机性，每次实验的差距变小，说明实验的性能更加稳定。对比基于量子谐振子的概率进行寻优的算法，自由粒子模型求解的结果更好，在eli51和bayg29数据上的数据对比尤为明显。这从侧面验证了自由粒子中的搜索模型更适合求解TSP，均匀分布采样过程在求解组合优化问题上比高斯采样具有一定的优势。在TSP中，由于解空间的离散化很难保证解之间的相互关系，这种相互关系在函数优化问题中体现得较为明显，一般最优解和次优解紧挨或者距离很近。这也就导致了算法求解过程中依高斯概率在当前次优解周围采样后的新解，回路距离减少不代表新解跟最优解的相对距离更近。这种相对距离可以理解成城市序列在相同位置上不一样的城市的个数。

3.2 拓展实验

本节是对自由粒子算法框架改进算法和其他启发式优化算法的对比实验分析。对比实验分析了自由粒子模型的算法跟HPSO、SA、GA、ACO性能。HPSO混合了遗传算法中的交叉变异操作，将标准粒子群中的速度更新和位置更新替换为粒子与个体最优和全体最优进行交叉的过程，算法的初始参数设置如下：粒子数目为1 000，进化次数为1 000；SA的初始参数设置如下初始温度为1000，终止温度为0.001，在每个温度下迭代500次，降温速率设置为0.9；GA的初始参数设置如下：种群个数为100，最大遗传代数为1 000，交叉概率为0.9，变异概率为0.05，选择进行交叉和变异的染色体数目的控制系数（有时被称为个体间的代沟）为0.9；ACO的初始参数设置如下：蚂蚁数量为50，信息素重要程度因子为1，启发函数重要程度因子为5，信息素挥发因子为0.1，最大迭代次数为1 000。在这些参数下相应的算法均能求解出相对较好的性能解。

为保证算法的稳定性，分别对6种算法进行了10次重复实验，对比了6种算法的最优值如表2所示，平均花费时间如表3所示，表中MV（Mean Value）表示10次重复实验中求解结果的平均值，MT（Mean Time）表示10次重复实验中求解所花时间的平均值。

表2 不同算法求解的最优值结果对比Tab.2 Comparison of theoptimal valuesobtained by different algorithms

表2中加粗数字表示不同算法求出的解中最好的结果。对比一些其他的优化算法，可以看出自由粒子模型算法的求解效果与HPSO、AS、GA、ACO在eli51、bayg29数据集上的求解精度有些差距，在burma14、ulysses16、ulysses22数据集上求解结果更好。在这些数据集中的MFPOA-DS比MFPOA求解的结果都是更优的，自适应尺度的变化有效提高了算法的求解性能。内部机制搜索的有效性保证了算法求解的可行性，自由粒子模型是一种基础的骨架模型，算法性能在此基础上通过一些策略机制的加入，可以进一步提高算法的性能。以上是对算法求解精度层面进行的对比，接下来对算法的求解时间上进行对比。

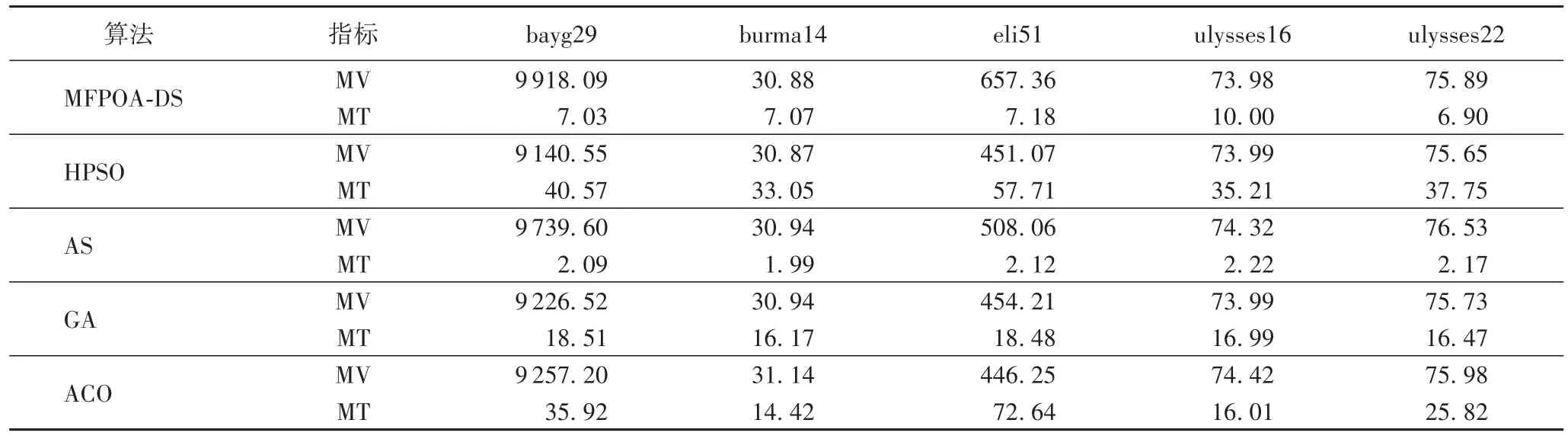
表3 求解TSP实例时不同算法求解时间的对比 单位：sTab.3 Solving timecomparison of different algorithms in solving TSPexamples unit：s

表4表示在不同的测试集上，MFPOA-DS相对HPSO、AS、GA、ACO在求解时间上减少的百分比，分别用IT1、IT2、IT3、IT4表示：

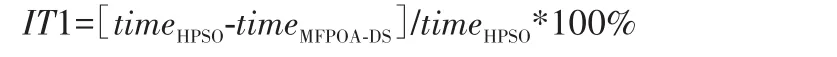
IT2、IT3、IT4同IT1。由表4可见，MFPOA-DS并不比AS算法有时间上的优势，所以表格中的数据为负值。

从相对节省时间数据可以得出，AS比其他算法求出最优解的求解时间最少，在时间复杂度上求解更优，在时间效率上MFPOA-DS仅次于 AS。相比HPSO、GA和 ACO，MFPOA-DS在5个测试集上将运行速度分别平均提升了80.42%、55.72%、66.45%。可见基于自由粒子简单结构构造的优化算法，具有更小的时间复杂度，能够快速、相对高效的求解组合优化问题。

值得注意的是，自由粒子优化算法结构简洁，在求解TSP时却有着比较好的表现。这种结构更适合对领域定义不是非常明确的问题，MFPOA的均匀分布结构对任何可行解都是同等看待，会使在可行空间上的搜索更加充分。后续工作会继续验证。

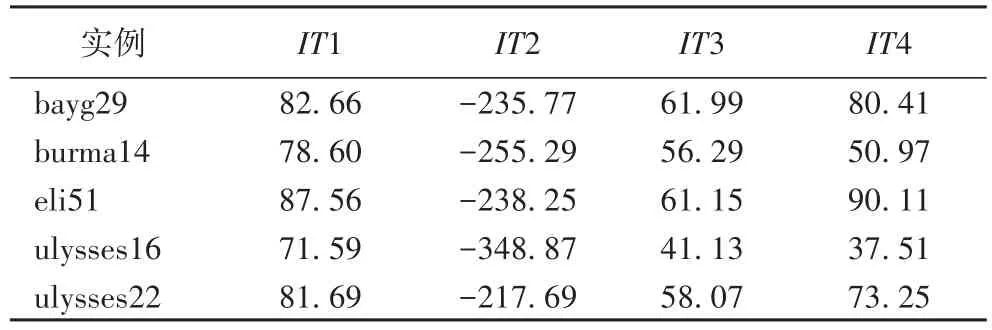
表4 不同测试集下MFPOA-DS相对其他算法在求解时间上减少的百分比 单位：%Tab.4 MFPOA-DSreducesthepercentageof thesolution timeof other algorithms respectively under different test sets unit：%

4 结语

多尺度量子自由粒子优化算法模拟了量子系统下自由粒子的简单运动过程，在优化问题中通过粒子在空间中的运动进行可行域中解的采样，根据采样信息对搜索空间进行缩放控制，实现在同一搜索尺度下的精细搜索和不同尺度下搜索中心的聚焦。自由粒子优化算法作为基于量子算法模型中的骨架模型，结构简洁，易于实现，通过对算法进行策略的改进，会使得算法的性能得到很好的提升。在自由粒子模型下的零势阱和谐振子模型下的高斯势阱的启发下，将优化问题中的目标函数进行势阱等效和泰勒近似实现量子模型下的转化，通过粒子在空间中的存在形式指导优化算法的寻优过程，实现量子模型的搜索机制。MFPOA和MFPOA-DS求解TSP的结果可以证明自适应尺度改进策略的有效性，MFPOA-DS改进算法与HPSO、AS、ACO和GA在TSP上的求解数据表明，MFPOA-DS算法在不同数据集上的求解结果表现不同，但在保持较好结果精度的情况下，在求解速度上比HPSO，ACO和GA平均提升50%，但是在求解精度方面算法并不总是比其他的优化算法最好，如何使算法的求解精度进一步提升成为下一步研究工作中的重点。

MFPOA的搜索结构简单，作为优化问题求解的一种基本的搜索框架，能够衍射出很多基于均匀分布为采样方式的算法。未来的工作将重点对算法的改进和算法间的联系进行深入研究，找出算法在不同应用上的优势。