动态事件时间数据的多任务Logistic生存预测方法
阮灿华,林甲祥
(福建农林大学计算机与信息学院,福州350002)
(∗通信作者电子邮箱ruancanhua@fafu.edu.cn)
0 引言
生存分析(survival analysis)是一种估计事件时间(timeto-event)的统计方法,已被广泛应用于临床医学、卫生保健、生物信息学、人口统计学、机械制造、经济学等领域[1]。在生存分析问题中,“生存”不仅可以指人或动物存活的状态(相对于死亡事件),还可以表示某药物的有效作用(相对于失效事件)、患者病情稳定的状态(相对于疾病复发或病情恶化事件),以及仪器设备的正常工作状态(相对于故障事件)等。因此,“生存时间”也是广义的,不单单是指通常意义下生物体的存活时间,而是泛指研究者所关心的某现象(如患者体征稳定)的持续时间。生存分析的核心问题是对事件时间进行估计,即预测某研究对象的生存时间或特定时间段内某事件未发生的概率。生存分析是研究特定人群寿命、各类慢性疾病、药物疗效以及提高医疗卫生服务的一项重要课题。例如,临床医学研究需要预估冠心病患者出院后下一次可能复发的时间;流行病学和生物学研究则需要检测样本从接触感染到发病所需要的时间;机械制造过程中人们常常对设备的可靠性进行测试,并估算故障发生时间(即设备使用寿命)。
传统生存分析方法按照生存时间分布假设及模型参数可以分为无参、有参和半参三种类型。无参模型主要包括Kaplan-Meier(KM)估计[2]、Nelson-Aalen 估计[3]以及生命表法(life table);有参模型通常假设事件时间服从某种特殊分布时,并采用正态、韦伯(Weibull)、log-Logistic等分布函数估计生存概率。然而,大多数情况下,关于事件时间的先验知识相对较少,因此应用局限性较大。半参(semi-parametric)模型的主要代表是比例风险(proportional-hazard)Cox回归模型[4],该模型具有简单易用的特点。近年来,机器学习方法也被广泛用于生存数据处理以及生存模型的参数学习:Leblanc等[5]提出了一种针对删失数据的分类回归树,即生存树(survival tree);Khan等[6]提出了一种针对删失数据的支持向量回归(Support Vector Regression,SVR)模型;杨铭等[7]针对复杂中医肿瘤临床数据提出了一种采用生存网络结构模型;潘浩等[8]提出了一种基于深度学习的Cox-Lasso生存分析方法用于肺癌细胞自动检测;Fisher等[9]针对纵向数据(longitudinal data)提出了一种动态Cox模型;Cortese等[10]提出了一种可以处理内在(internal)风险因子变量的多状态对比风险模型;Wang[11]提出了一种针对动态风险因子的数值插入法以及对未知链接函数进行估计的动态比例风险模型。
研究事件发生规律常常需要对样本进行长期追踪,因此本文需要处理的事件时间数据包含大量随时间变化的风险因子变量(如哮喘病患者在不同时间点的血液含氧量和二氧化碳分压观测值)。然而,现有的生存分析方法大多无法有效处理这类复杂的动态数据,这些方法通常采用简单的单点取样[12](如当前值抽样和平均值抽样),在估计某时刻的生存概率时只考虑当前记录时间点的风险因子变量值而忽略历史数据的作用,这在许多实际应用中并不合理,例如哮喘患者在服用β2激动剂之后,本文会观测到生理指标一秒钟用力呼气容积(Forced Expiratory Volume in one second,FEV1)在很长一段时间内都会受该药剂影响,因此某一时刻的FEV1观测值并不能刻画病人的病情发展以及变量FEV1与生存概率之间的关系。总体而言,如何有效分析复杂的动态事件时间数据、构建事件时间预测模型是一个亟待解决的难点和热点问题,因此,本文的工作重点是探究刻画风险因子变量观测序列的数据模型以及生存机器学习方法。
事件时间数据作为一种特殊的观测型数据,包含大量删失数据,可以用于事件预测模型学习的事件时间信息多有缺失。多任务学习方法能够为每个训练任务提供更多的信息,从而提高模型精度并降低预测错误率,例如,多任务学习预测病情发展、HIV(Human Immunodeficiency Virus)治疗、基因数据分析等[13-14]。鉴于此,本文提出了一种多任务Logistic生存学习模型(Multi-task Logistic Survival Learning,MLSL),该模型将生存预测任务转化为一系列不同时间点的Logistic生存回归学习与分类问题,即多任务学习与预测。针对风险因子变量的动态观测值,本文将构建一个新的全数据生存函数,利用所有可观测值估计累计事件风险,提高数据利用率;另外,本文的新方法利用Logistic回归模型分别估计事件样本和删失样本在不同时间点的事件概率,并根据各时间点的概率对事件时间进行估计。为了学习MLSL模型的参数,本文在优化目标函数中对模型参数进行了正则化和平滑处理,避免模型过拟合。最后,本文在多个临床事件时间数据上开展对比实验,并验证模型的有效性和实用性。
1 生存预测
本章介绍事件时间数据,并描述动态事件时间数据特性以及Logistic生存函数和概率模型。
1.1 事件时间数据
不同于一般类型的数据,事件时间数据是一种特殊的观测型数据,常常包含右删失(right-censoring)、左删失、区间删失等类型的事件删失样本。事件删失的主要原因有以下两种:
失访 某些与研究无关的原因导致样本无法访问,如肺癌患者在随访期间死于心肌梗塞、自杀或车祸。
追踪终止 追踪在事件发生之前终止。
如图1所示的7个样本中,A、B、G的初始观测时间未知,即事件左删失;样本B、C、E中途退出实验,G在追踪终止时仍未有事件发生,这4个样本都属于事件右删失类型。本文主要针对最常见的右删失类型数据开展模型研究和应用研究。

图1 事件时间数据示例Fig.1 An exampleof time-to-event data
1.2 动态事件时间数据
样本i在t时刻的D个风险因子变量的观测值记为x(i t)=(xi(1t),xi(2t),…,xiD(t))。对于给定数据集,假设所有非删失样本的事件时间点为τ1<τ2<…<τK。给定风险因子变量观测时间点集合为φ,动态事件时间数据X i=(x(i u1),x(i u2),…,xi(u|φ|)),其中uj∈φ是风险因子变量观测时间点。特别地,本文用φ(t)表示在时间t之前的所有观测时间点。生存状态zi为表示事件是否发生的二元变量,即zi∈{0,1}:当i的事件已发生则取值为1,否则为0;标签时间变量yi∈R+在zi=1时为生存时间Ti,即yi=Ti,而当zi=0,则为删失事件时间Ci,即yi=Ci。本文用E1={i|zi=1}表示追踪期内有事件发生的所有样本。对于删失事件样本,本文无法在追踪期内观测到事件是否发生,也无法得知其在追踪期外的生存状态,但至少本文已知在丢失其可观测的最后时间点之前仍是“存活”的。换言之,右删失样本的生存时间大于或等于删失时间,即Ti≥Ci,∀i∈E0,集合E0={i|zi=0}包含所有追踪期内没有事件发生的样本。
1.3 Logistic生存函数
生存预测的核心任务是预测事件时间,即预测事件在某时间点发生的概率,其概率密度函数为F(t)=Pr(T≤t)。生存函数S(t)表示t时刻的生存概率,即事件不会早于t发生的概率,因此S(t)=Pr(T>t)=1-F(t)。实际上,任意形式的分布(如指数分布、Weibull分布、正态分布),只要满足时间变量t∈[0,∞)都可以作为生存分布假设[15]。例如当且仅当lnT=η+σU时(U∈(-∞,∞)为随机变量),T服从log-Logistic分布,生存概率则为:

从式(1)可以看出,生存函数与风险因子变量无关,因此传统的log-Logistic有参模型无法估计风险因子变量对事件发生的影响。本文改写η为风险因子变量的线性函数,并构造如下生存函数:

这里,参数w刻画了风险因子自变量在t时刻对事件发生的瞬时作用。生存函数S表示观察对象随访到t时刻的累积生存率,该生存概率只由当前观测值决定,而风险因子观测值的变化对事件时间的影响作用被忽略。
2 多任务Logistic事件时间预测
本章给出新的风险累积Logistic生存函数和多任务学习方法、回归模型系数的选择策略,以及事件时间估计方法。
2.1 风险累积Logistic生存函数
为了估计风险因子变量在整个观测期内对生存概率的累积作用,本文构建以下Logistic生存函数:

其中Ri(u,W)是i在观测时间点u的累积事件风险,计算如下:
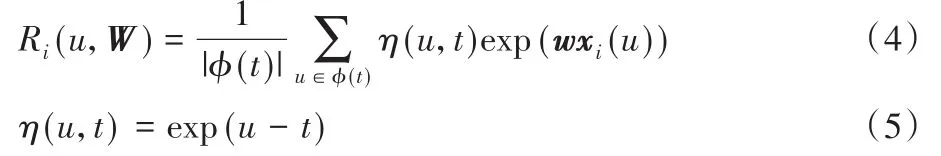
指数函数η(u,t)为u时刻的事件风险到t时刻的衰减率,取值范围为(0,1],即时间越久,风险衰减越多。换言之,累积生存函数可以充分利用观测数据,更符合临床应用中的实际情况,例如病人用药之后的很长一段时间内,生理指标都会受到药效影响,且该影响会随着时间变小。
2.2 多任务生存学习
实际上,风险因子变量与事件发生概率之间的关系是随时间而变化的,因此本文设定一个新的回归系数矩阵W=(w0,w1,w2,…,w K)用于描述风险因子变量对生存概率的潜在影响力:w k是在tk时刻的D维回归系数向量。样本i的生存状态在观测期内的变化可以表示成一个二元序列,zi(τ2),…,zi(τK)),当t≤Ti时,zi(t)取值为0,t>Ti时则取值为1。为了求取最优的回归系数W*,本文将优化关于W的似然函数。该似然估计实际上是在给定参数时对z i概率的估计。给定i∈E1,关于W的似然函数为:
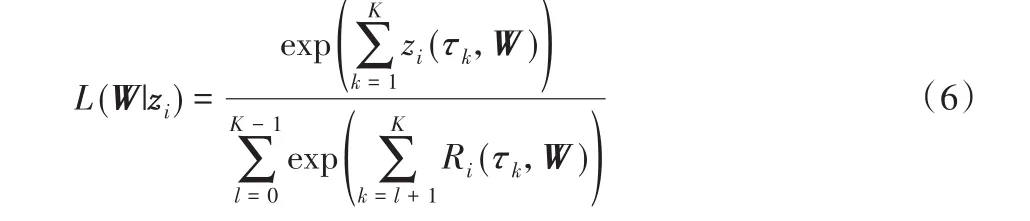

最大化似然函数可以转化为最小化似然函数的负对数,由此,本文的学习任务为:


2.3 正则化系数选择
正则化系数λ可以在验证集上采用交叉验证方法进行优化。为了避免优化过程中目标函数出现常数项,本文对训练集风险因子变量矩阵X和验证集风险因子变量矩阵U的各列,以及训练集事件输出列向量Y和验证集事件输出列向量Q都进行标准化处理。最优的λ值能够使得模型在验证集上的预测错误率最低,因此正则化系数优化的核心是解决下述最小化问题:

为了计算方便,上述优化问题的解可以近似估计为ridge回归模型的正则化系数最优解,因此

目标函数O关于λ的偏导数为:

根据推论1以及矩阵计算,本文可以得到:

将式(11)和式(9)代入式(10),并令J=XTX+λI,则本文有:
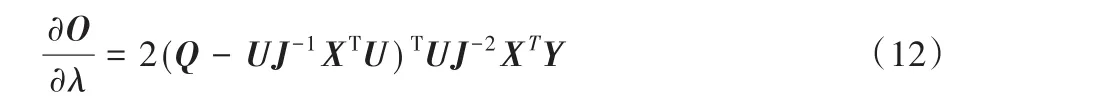
式(12)包含大量的矩阵转置计算,难度大且效率低,因此,本文用XTX的分解特征值来改写式(12)。假设矩阵V的每列为特征向量,γ为特征值向量,那么XTX=Vdiag(γ)VT。G=XTX+λI的特征向量仍然为V,特征值则为γ+λI。因此,本文有G=Vdiag(γ+λI)VT。假设P=diag((γ+λI)-1),P-1=VPVT,则

推论1 假设M是一个基于实参κ的方阵,且各分量函数可导,M(κ)对于所有的T都是可逆的,那么d
证明假设mij(κ)是M的分量函数,mjk(κ)是M-1(κ)的分量函数。给定矩阵M的阶n以及克罗内克(Kronecker)函数,对于任意κ,本文有:

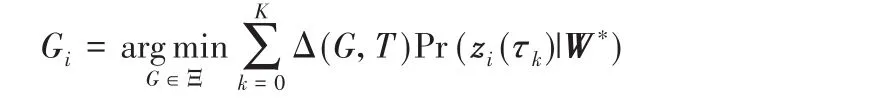
其中Ξ={τ1,τ2,…,τK}。损失函数Δ(G,T)为预测事件时间G和真实事件时间T之间的误差,如绝对误差|G-T|或对数误差|lnG-lnT|。
2.5 模型分析
本文的多任务回归学习方法将生存函数(曲线)的拟合问题转化为各时间点的生存状态预测问题。这些预测任务是紧密相关的,各时间点的预测结果满足生存概率的单调性。
与参数模型相比,本文的新模型无需生存时间分布假设,而且可以给出各时间点的事件风险率以及风险因子变量对风险率的影响,具有一定的普遍适用性。Cox模型采用比例风险假设,并估计生存概率为:

其中:基线风险H(0t)为不考虑风险因子变量时的累积风险,通常由Breslow估计法[16]确定;基线概率SCo(xt)=S(t(|0,0,…,0)),表示在t时刻的基准死亡比例(即发病密度或死亡密度)。回归系数β描述了生存概率与风险因子变量之间的关系,该关系不随时间变化而变化。静态回归系数简单,但却不如本文的动态回归参数更符合实际情况,这也是动态Cox(Time-dependent Cox,TCox)模型[9]采用动态系数βk的主要原因。类似地,Cox的半比例风险(Semi-Proportional Hazards,SPH)[17]模型也采用动态回归系数。与SPH模型的全数据学习方法类似,新模型充分利用删失数据优化参数。本质上,新模型和基于Cox的模型采用的都是风险乘积方式。
新模型中的全数据似然函数不同于Cox模型的最大化如下局部似然估计(Maximum Partial Likelihood Estimate,MPLE)[18]函数:

2.4 事件时间预测
模型学习在训练样本上优化生存函数参数并得到最优值W*。因此,对给定风险因子变量值Xtest的测试样本,本文用Logistic回归函数估计生存概率为S(t|Xtes)t=(1+R(i u,W*))-1。鉴于生存函数只能估计生存概率,且目前尚没有具体的生存时间估计方法,本文对样本i的事件时间估计如下:
其中χ(yi)是在时间yi前所有未有事件发生的样本。另外,新模型的目标函数没有采用传统的Elastic-Net[19]惩罚因子
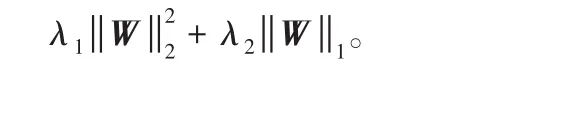
3 实验
本章首先说明数据集及预处理工作,接着给出对比模型和性能评价标准,最后介绍实验过程并根据实验结果对模型的有效性和效率进行分析。
3.1 实验数据及预处理
本实验将在如表1所示的10个数据集上开展,其中,Lung、Prostate和Colorectal三个癌症数据集是由NIH CDAS(https://cdas.cancer.gov)提供;其他7个数据集从R database获得,且本文利用tmerge函数[20]为每个数据集生成动态风险因子变量值。为了减少观测值差异对相似度度量的影响,本文将数值型数据集的观测值都进行标准化处理。对于类属性变量,本文利用虚拟变量法(dummy variable)将其转化为0-1二元变量,这样所有风险因子变量便可以直接用于回归模型的计算。虚拟变量法的核心是将有l(l≥2)个观测值的分类型风险因子变量用其中任意l-1个观测值所构成的0-1二元虚拟变量所表示。例如,生理指标BMI(Body Mass Index)一般有“体重过轻”“正常”“超重”和“肥胖”四个类属性变量值,本文任选三个变量值作为虚拟变量来描述变量BMI。假设(体重过轻、正常、超重)为一组虚拟变量,每个虚拟变量取值1(“是”)或0(“否”),(0,0,0)则表示“肥胖”。本文都从每组数据中抽取10%的样本作为验证集用于选择MLSL的正则化系数。
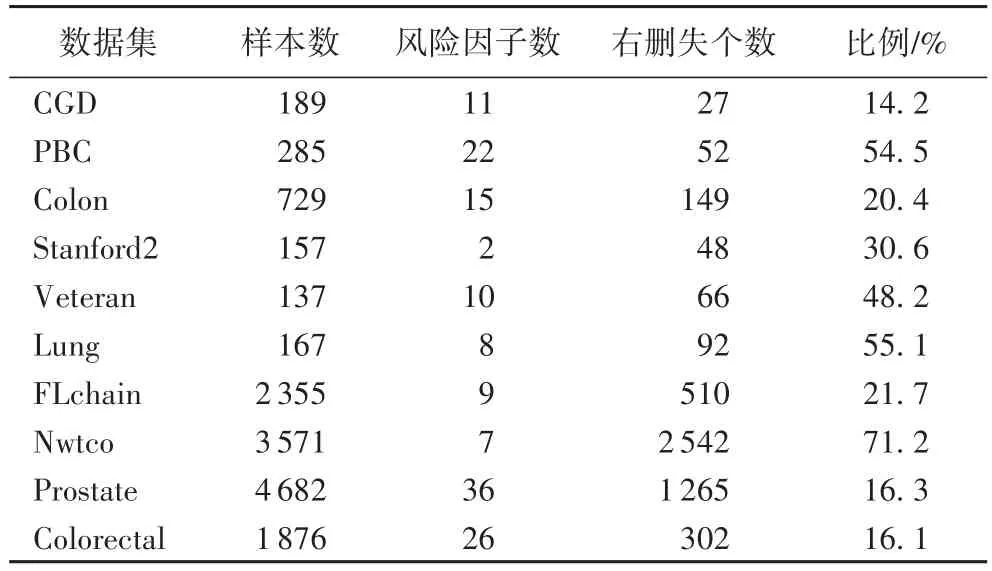
表1 事件时间数据集统计信息Tab.1 Statisticsof time-to-event datasets
3.2 对比模型
本文将MLSL与以下6个具有代表性的生存预测模型作对比:
1)TCox,即动态 Cox模型[9],由 R 提供的 survival宏包实现。
2)CoxEN,即弹性网络(Elastic-Net)规范化Cox模型[19],由R宏包survival和glmnet实现。
3)RSF,即随机生存森林(Random Survival Forest)[21],可以用randomForestSRC包实现,模型参数为R函数默认值。
4)Cox-TRACE,即基于Cox的迹准则多任务生存分析模型,由文献[22]提供的开源代码实现。
5)SPH,即半比例风险模型,以Cox为基础用于处理序列型特征变量,本文对比实验采用与文献[17]相同的参数设置。
6)AFT,即叠加失效时间(Accelerated Failure Time)模型[23],假设事件时间满足 Weibull分布,由R函数WeibullReg实现。
3.3 评价指标
为了评价各模型的生存概率预测能力,本文采用常用的AUC(Area Under the Curve)和C-index[24]作为评价指标。在随访学习结束时,预测事件是否发生是一个二元分类问题,因此本文采用如下的AUC指标检测模型的预测(二分类)能力:

其中:I是0-1示性函数,t0为随访时间。
C-index指标是AUC指标的泛化形式,用于评价模型概率预测的能力。若数据集共有n个可以按照真实事件时间排序的样本组合,则:
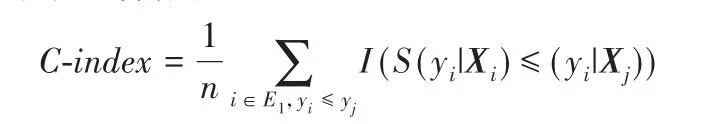
其中:i∈E1,yi≤yj表示所有可排序的样本组合i、j。C-index统计在各观测时间点yi所有满足预测事件概率的排序与真实事件时间排序一致的样本对i、j的个数,并考虑了生存并列(ties)样本的存在[25]。AUC和C-index指标的取值范围通常是0.5(完全随机预测)到1.0(最佳预测)。
为了检测模型预测事件时间的准确率,本文对比预测时间G和真实事件时间T之间的误差,并定义如下相对错误率(Relative Error rate,RE):
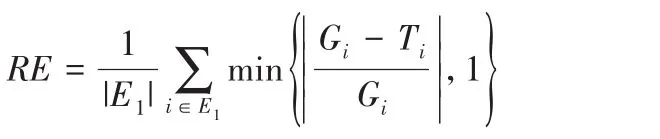
显然,RE值越小,模型预测的事件时间越准确。
3.4 结果与分析
3.4.1 生存预测结果对比
每个模型在10个数据集上各进行100次10折交叉验证,所得结果的平均值为最终结果。表2的每个单元格列出了平均AUC和平均C-index值,同时表3给出了对应的MLSL模型正则化系数。

表2 各模型关于AUC和C-index指标的预测结果比较Tab.2 Comparison of prediction resultsof each model in termsof AUCand C-index
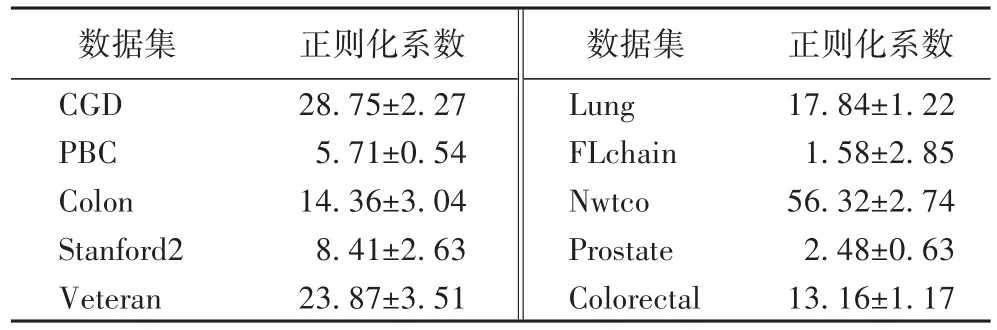
表3 MLSL正则化系数Tab.3 Regularized coefficientsfor MLSL
表2结果表明不论是对于删失比例很高的PBC、Nwtco、Veteran和Lung四个数据集,还是在样本数和维度都较大的Prostate和Colorectal数据集上,MLSL均获得了较高的预测精度,由此可见本文提出的MLSL模型对各类复杂数据具有较强的适用性。尽管对比模型能够在个别数据集上取得较好的结果,如SPH在CGD和Lung数据集上,Cox-TRACE在Standford2数据集上达到或超越了MLSL的预测精度,但是整体表现不如MLSL,其主要原因就是这两个模型是基于Cox的等比例风险假设。同样地,TCox和CoxEN鲁棒性也较差。参数模型AFT在所有数据集上都表现较差,原因在于Weibull分布假设并不符合大多数数据的真实情况。值得注意的是,多数情况下,模型在同一数据集上获得的C-index精度往往比AUC略低,这是因为C-index作为泛化的AUC,在计算过程中需要对全部样本生存时间进行精确排序,难度较大。
表4给出了模型在测试集上的事件时间预测结果的相对错误率。除了在FLchain数据集上相对错误率比SPH的稍大以外,MLSL关于事件时间的预测结果都是最好的,这主要得益于全数据学习和多任务学习对生存概率的估计和生存函数参数的优化。另外,生存函数本身也对事件时间的预测起决定性作用,本文的Logistic生存函数只需要在参数得到优化的情况下就可以较精确地拟合数据集中的样本生存概率分布。然而,基于Cox的方法虽然在参数学习过程不需要估计基线风险,但是在预测生存概率和事件时间时则需要用到某些参数估计方法(如Breslow估计)[16],从而影响了预测准确率。
3.4.2 生存概率曲线对比
图2绘出了一位67岁的男性肺癌(Lung)患者和一位82岁女性直肠癌(Colorectal)患者在一年内(52周)的生存概率曲线。肺癌患者和直肠癌患者的生存时间分别为13周和10周,因此从理论意义上说,从第13周开始,肺癌患者的生存概率为0,即S(t>13)=0,而直肠癌患者则从第10周开始生存概率应当为0,即S(t>10)=0。从图2(a)可以看出MLSL在第13周时所预测的生存概率最低,且早在第8周,MLSL预测该肺癌患者的生存概率低于50%,远比其他预测模型所得到的生存概率低。在图2(b)中,MLSL预测的结肠直肠癌患者生存概率在第10周之后是最低的。由此可见,MLSL模型具有一定的预警能力,能够尽早发出警告,这在临床决策具有相当重要的意义。另外,目标函数中的参数平滑处理使得MLSL生存曲线要比其他曲线略微平滑。
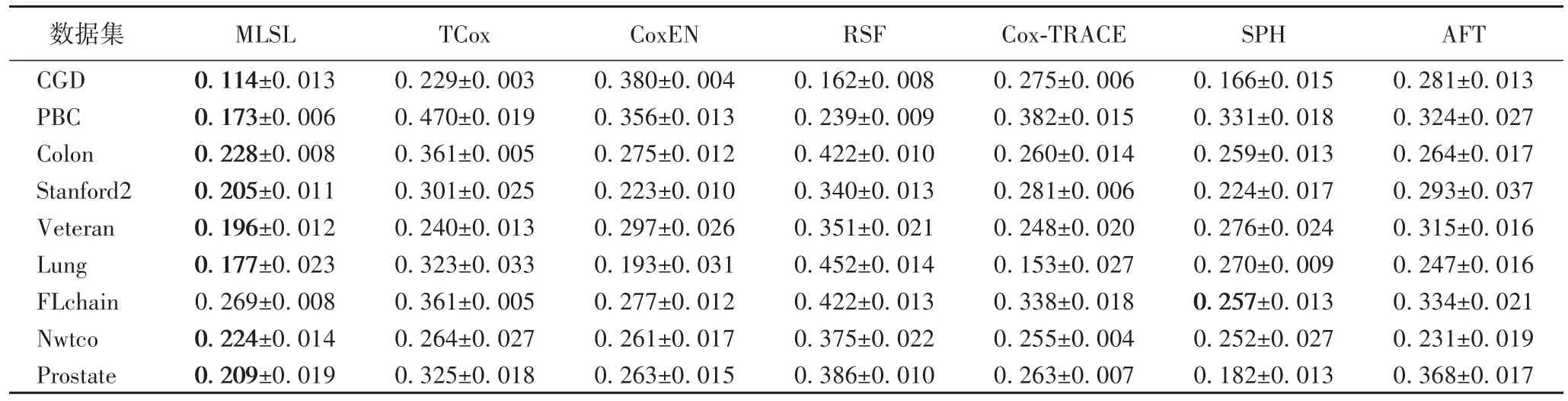
表4 事件时间预测的相对错误率比较Tab.4 REcomparison of predicted time-to-events

图2 各模型预测的生存概率曲线对比Fig.2 Comparison of predicted survival curves by different models
3.4.3 模型效率对比
对比实验中预测模型的测试效率都较高,且差异不明显,因此本文只给出各模型的训练效率。图3列出了各模型在10个数据集上的训练时间(单位:s)。由图可见,MLSL在大数据集上的效率高于同样采用动态系数的TCox模型,这主要是由于新模型的似然估计对每个样本的生存概率估计是相互独立的,目标函数收敛速度比偏似然估计快。CoxEN需要估计两个模型参数,当风险因子变量较多时,参数优化消耗时间较多,因此处理维度较高的数据时效率较低。RSF模型中,树节点的分裂过程需要评估log-rank结果,训练时间受样本数量影响较大,因此处理不同规模数据的效率差异明显。SPH优化具有瞬时风险约束条件的目标函数,模型复杂度相对较高,算法迭代次数增加,因而其运行时间也有所增加。
为了进一步分析MLSL的泛化能力,本文检测了MLSL的效率与样本数量N和数据维度D之间的关系。以Prostate数据为例,本文重新合成该数据集,分别调整N和D并测试MSLS的效率:固定数据维度D=30,并不断增加样本数量,MLSL的运行时间与样本数呈线性关系,如图4(a)所示;当固定样本数量N=3500,并不断增加风险因子个数,MLSL的运行时间与维度D也呈现线性关系,如图4(b)所示。以上结果表明本文的MLSL具有很强的泛化能力,适用于不同规模的数据。

图3 MLSL的训练时间与数据规模和数据维度之间的关系Fig.3 Relationship between training time and data size/dimensionality of MLSL
4 结语
本文提出了一种针对动态事件时间数据的多任务Logistic生存学习模型MLSL。新模型通过全数据学习方式估计事件样本和删失样本的生存概率,并构建了具有参数正则化约束和平滑约束的优化目标函数。MLSL将生存预测转化为一系列在不同时间点的Logistic回归学习任务,无需未知数据生存分布假设,同时增强了模型对删失数据的预测能力。针对动态数据的特性,MLSL刻画了风险因子序列特征,并估计事件累积风险。与传统方式相比,新模型能够挖掘出风险因子变量与生存概率之间的潜在关系。在实际临床数据上的对比实验结果表明,MLSL可以有效地预测动态事件时间数据,其预测精度优于目前经典的生存分析方法,并且大幅度提升了预测结果的稳定性。

