水下多缆多体拖曳系统运动建模与模拟计算

王 飞，丁 伟，邓德衡，吴小峰

(1. 上海交通大学 海洋工程国家重点实验室； 高新船舶与深海开发装备协同创新中心， 上海 200240； 2. 武汉第二船舶设计研究所， 武汉 430064； 3. 中国船舶科学研究中心， 江苏 无锡 214082)

水下拖曳系统作为一种基本的水下探测装备，广泛应用于海底探测、军事反潜、海工应用等领域，能否准确预知其在各种情况下的空间姿态及动力响应特性，是拖曳系统设计与应用中的重要问题.拖曳系统通常由水面拖曳母船、牵引缆、水下拖体、阵列、尾绳等设备组成，拖曳形式也因用途的不同而千变万化[1-2].现代新型拖曳系统为了增强探测能力，开始向多阵列(拖缆)多拖体系统发展，一个系统中可包含数个阵列、数个拖体或其组合，效率显著提升；但系统也因此变得更为复杂，实际应用中也暴露出一些问题，如运动响应特性不明晰、缆索纠缠、海底触碰，这些问题常会对系统的正常运行造成影响.

水下拖曳系统动力学的理论研究在很早就已经广泛展开，国内外众多学者针对各自的研究目标，建立运动数学模型，采用数值模拟等方法来研究其在不同情况下的运动响应特性，包括各种稳态运动研究及动态运动研究.稳态运动研究方面，Wang等[3]在前人研究结果的基础上，针对多种形式的拖曳系统，较为全面地考虑了各种情况下的稳态运动，建立初始值方程，提出了多维嵌套二分法进行求解，以解决诸多实际问题，并将其应用到系统设计中去.系统的动态运动研究更为广泛，通常研究人员在拖缆运动微分控制方程的基础上采用集中质量法、有限差分法等，来分析其在各种情况下的动态运动[4-12].Huang[4]最早提出了集中质量法来计算拖缆的动态运动响应，它们能够很好地预报拖缆系统在正常状态下的运动.在此基础上，国内外众多学者展开了卓有成效的拓展性研究[5-12]，内容涉及水下拖体耦合动力学研究[5,7-9]、拖曳系统导杆影响分析[10]、系统收放模拟[11]、海底缆铺设运动研究[12].

多阵列拖曳系统作为近些年出现的一种系统，相关研究文献较少，其在不同情况下的运动响应特性不甚明晰.为此本文针对水下多阵列多拖体拖曳系统，展开基础研究工作，探讨其在不同情况下的稳态和动态运动响应特性.拟采用集中质量法建模思想，结合潜艇6自由度运动控制方程，建立拖缆(阵列)及拖体的运动控制方程，并通过建立不同的连接耦合边界条件将其耦合成一个整体.通过数值模拟研究系统在各种不同情况下的运动响应特性，以期给出一些规律性结论.

1 系统运动建模

本文将拖缆(阵列)视为理想的柔性缆索，忽略缆弯曲及扭转刚度的影响； 鉴于水面拖曳母船的排水量逾3 000 t，且配有航迹姿态控制系统，本文忽略缆对水面拖曳母船的耦合作用；因各个缆的运动控制方程均一致，简便起见A、B、C、D 4根拖缆(阵列)的参数符号全文统一表示，不再单独指明.

典型的多阵列拖曳系统如图1所示，其中水下拖体内部载有多种测控设备，并连接4根拖缆，缆A为牵引缆，水中长度可调整用以进行变深控制，缆B和缆C为近乎0浮力的阵列缆，缆D下端为一小型拖曳设备.水下拖体尺度较大，对系统运动有重要影响，本文采用6自由度运动建模，而缆D下端的小型设备则将其视为质量点进行简化建模处理.对于每一根拖缆(阵列)，s为缆长坐标，S为其总长，其中拖缆下端/尾端的坐标记为s=0，(θ,φ)为拖缆微元姿态角，方位角θ为缆顺时针偏离y轴的角度，φ为抬升角，这两个角度取决于缆的空间位置.水下拖体的3个姿态角，参考潜艇操纵性运动分别定义为：艏向角ψ，为艏向水平偏离y轴的角度，顺时针为正；纵倾角ϑ，抬艏为正；横倾角φ，右倾为正.

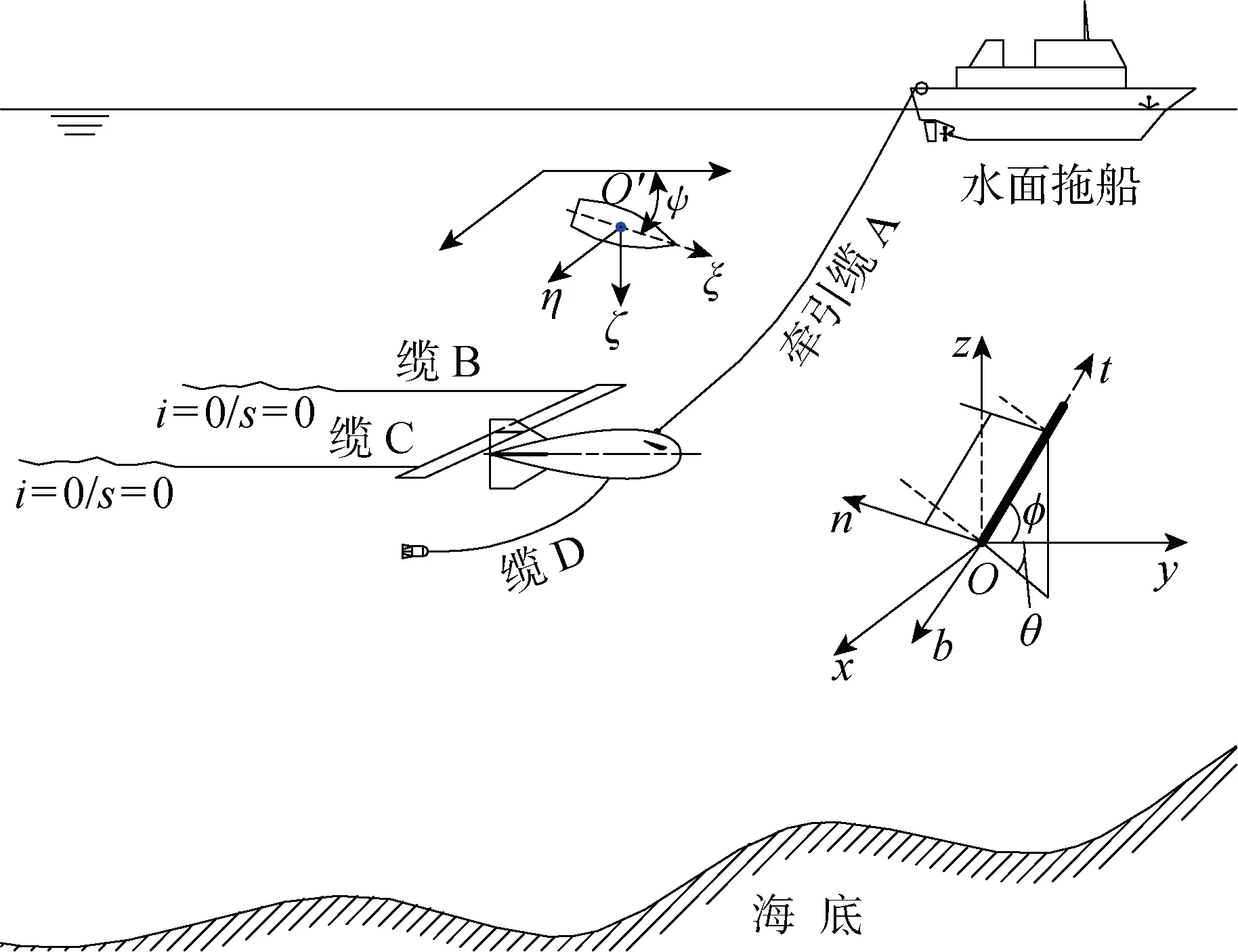
图1 水下多缆多体拖曳系统Fig.1 Multi-cable multi-body towed system

1.1 坐标系统

建立3个坐标系统描述整个系统的运动：惯性坐标系(Oxyz)，拖缆局部坐标系(Obtn)和拖体/拖船运动坐标系(O′ξηζ).其中惯性坐标系原点位于水面，z轴垂直向上；拖缆局部坐标系附于拖缆上，t轴为切向，n为法向，b为侧法向；拖体运动坐标系随拖体运动，ξ轴指向船首，η轴指向右舷，ζ轴指向下方.这3个坐标系通过姿态角相互关联，其转换关系为

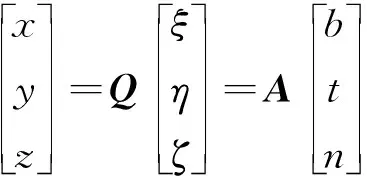
(1)

式中：Q与A分别为拖体和拖缆坐标系转换矩阵.

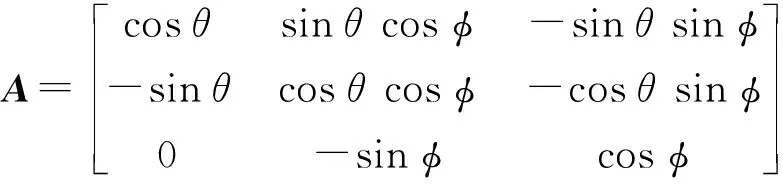
1.2 拖缆运动控制方程

拖缆微元的控制方程为

(2)

式中：M为拖缆微元质量矩阵；T为张力；D为阻力；G为重力；B为浮力；x为其空间位置向量.

根据集中质量法思想，将一拖缆从尾端至上端离散为N段，即N+1个节点，其中：尾端s=0，为第i=0个节点；上端s=S，为第i=N个节点.

对第i个节点应用牛顿第二定律，得拖缆节点的基本运动控制方程：

(3)

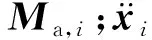
1.3 拖体运动控制方程

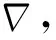
XH+XS+∑Xci

YH+YS+∑Yci

ZH+ZS+∑Zci

MH+MS+∑Mci

其中：(u,v,w,p,q,r)为拖体的线速度及角速度；I为各个方向上的转动惯量；方程右侧(X,Y,Z,K,M,N)为作用在拖体上的力和力矩；下标H表示拖体水动力；下标S表示拖体重浮力作用分量；下标c表示拖缆作用力.拖缆作用力将作为边界条件在1.4节给出.

拖体的重浮力作用力为

作为运动关联条件，水下拖体的姿态角同角速度有如下关系：

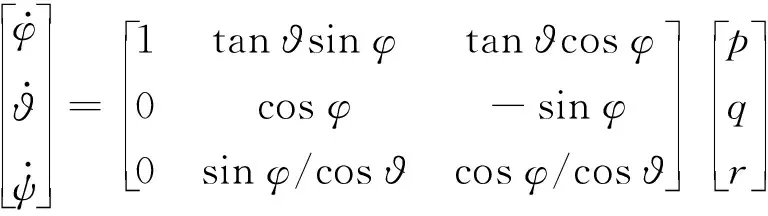
1.4 边界条件

在拖曳系统运动过程中，拖缆与水下拖体/水面拖船是相互作用、相互影响的.根据不同的情况，有3种不同的边界条件：拖缆自由端边界条件、拖缆下端边界条件和水下拖体(水面拖船)-缆耦合条件.为简便起见，一些公式中将拖缆节点的下标忽略不写.

(1) 拖缆自由端边界条件.对于没有拖体的自由端(缆B和缆C)，视其为一节点，应用集中质量法控制方程：

(4)

式中：I为单位矩阵；l为节点间长度；g为重力加速度；下标1/2表示节点0和1之间的物理量.

(2) 拖缆下端小型设备边界条件(缆D).该处设备尺度相对很小，可直接将其溶入到缆的控制方程，采用3自由度运动方程进行求解：

(5)

式中：Md为小型设备的3自由度质量及附加质量矩阵；Fd为其上的作用力，

右式第1项为其重浮力，第2项为其运动阻力，Sd为设备的特征面积，Cd为其阻力系数.

(3) 水下拖体(水面拖船)-缆耦合边界条件.在拖缆与拖体连接点处边界条件包括运动条件和动力条件，本文将连接点处拖体的位置和速度作为运动耦合边界条件，以确定拖缆连接节点的位置速度；而拖缆的张力作为动力耦合边界条件，融入到拖体操纵运动控制方程.

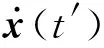
(6)

式中：t′为时间；(xt,yt,zt)表示拖体在惯性坐标系下的位置；Rtp为拖体坐标系下连接点的坐标值.

作为动力耦合边界条件，拖缆作用于拖体的作用力(如缆A下端，其余类似)，经过坐标转换可以表示为

水面拖船的位置与速度为整个系统的输入，是已知的时间函数；而水下拖体的位置与速度则由拖体的运动控制方程计算得到.

1.5 系统稳态运动求解

系统的稳态解通常作为动态运动的初始条件.各拖缆的稳态运动控制方程在局部坐标系下为

(7)

式中：u、d、σ分别为缆的单位长度质量、直径、截面积；u=(ub,ut,un)为局部坐标系下缆的速度；T为拖缆张力；Ct、Cn分别为切向、法向阻力系数；ε为缆的应变.

拖缆位置在惯性系下的微分关系为

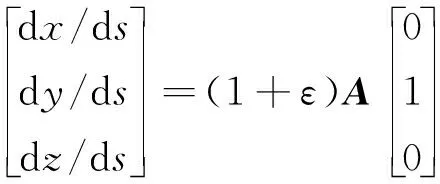
对此稳态运动控制方程，采用4阶龙格库塔积分从拖缆下端开始沿缆长积分，得到整个拖缆的稳态解，拖缆在下端的初始值(T0,θ0,φ0)根据不同的情况分别如下：

(1) 拖缆自由端初始值.对于缆B和缆C的自由端，拖缆张力与欧拉角的变化率均为0.因拖缆侧向无作用力，姿态角

θ≡ const=ψ

所以可以将稳态问题转换到二维空间下求解，最终拖缆的初始值为

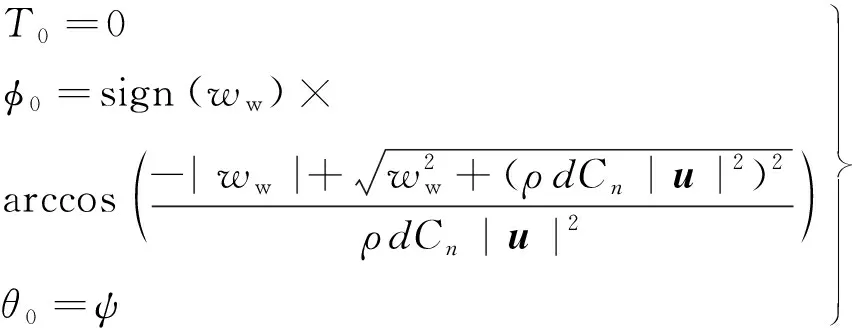
(8)

式中：

ww=(μ-ρσ)g

ww为缆在水中单位长度重量，

(2) 水下拖体连接点初始值.对于缆A以及缆D的下端，可以由作用在拖体上的外力来确定拖缆的初始值，

(9)

式中：Fx、Fy、Fz为作用在水下拖体上除该拖缆以外的外力.

(3) 水下拖体稳态求解.由于拖体的控制方程是一个高阶的非线性系统，其稳态解不能解析计算，本文在缆B以及缆C张力稳态解的基础上，采用动态计算足够长时间的方式得到其稳态解(u,w,ϑ)，而拖体的横向速度和横倾角均为0，艏向角则为系统的艏向角.

2 控制方程数值求解

由式(3)可得各拖缆的运动控制方程：

(10)

将式(10)与拖体运动控制方程和边界条件联立，可得到整个系统的运动方程，并采用4阶龙格库塔方法在时域内积分求解.由于控制方程是条件稳定的，计算时间步长必须很小，一般为毫秒级.

3 仿真计算与分析

整个拖曳系统由4个拖缆、1个拖体和1个小型拖曳设备组成，属短阵高航速系统，其主要参数如表1和表2所示，海水密度取为ρ=1 025 kg/m3，无海流，牵引缆上端连接于水面拖曳母船，水面母船的位置与速度为整个系统的输入量.4个拖缆同拖体连接点坐标分别为A(0, 0, 0) m，B(-1.7, -1.1, 0) m，C(-1.7,1.1,0) m，D(-0.2,0,0.62) m.整体上拖缆以5 m的间距进行离散，在曲率变化较大的地方适当加密，拖缆节点数量共126个，计算时间步长取2 ms.

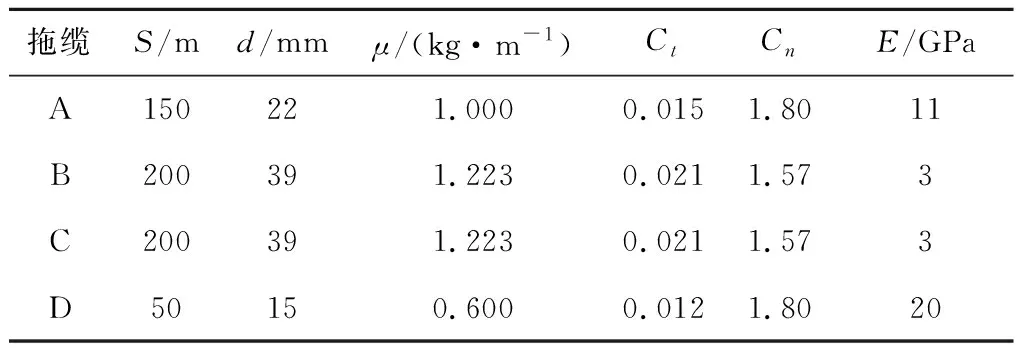
表1 各拖缆物理参数Tab.1 Physical parameters of the towed cables

表2 水下拖体参数及无因次惯性类水动力导数

Tab.2 Parameters and non-dimensional inertial derivatives of the underwater towed body

参数取值长度/m2.72质量/kg673体积/m30.312重心/m(0.02, 0, 0.46)浮心/m(0.00, 0, 0.22)Z'q·,M'w·0.01570K'p·-0.00207K'r·,N'p·0.00020M'q·-0.00278N'r·-0.00371X'u·-0.0067Y'v·-0.0763Y'p·,K'v·0.00682Y'r·,N'v·0.0159Z'w·-0.0861Ixx/(kg·m2)170.4Iyy/(kg·m2)197.6Izz/(kg·m2)175.3Ixz/(kg·m2)6.2

鉴于水下拖体一般无大幅机动，水动力仅取主要项，各无因次导数分别为

缆D下端小型拖曳设备的参数为：质量61 kg，体积0.028 m3，其质量矩阵(单位：kg)及作用力(单位：N)近似为

3.1 稳态运动计算与分析

系统的稳态计算结果作为下文动态运动计算的初始条件.

本节拖曳速度v=4,6,8,10 kn，方向沿y轴正方向，水面拖船拖曳点位置为(0,0,0) m.经计算得到不同速度时系统的稳态结果， 如表3、图2和图3所示.其中牵引缆上端的张力分别为Ti=N-1/2=5.7,8.6,13.5,20.2 kN，阵列缆尾端在水下的深度分别为z=-74.2,-47.6,-33.7,-25.2 m.

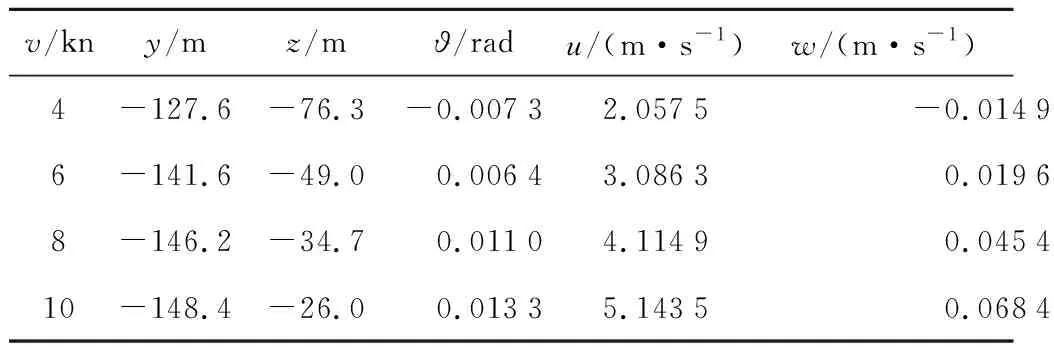
表3 拖体的稳态参数Tab.3 Steady state parameters of the towed body

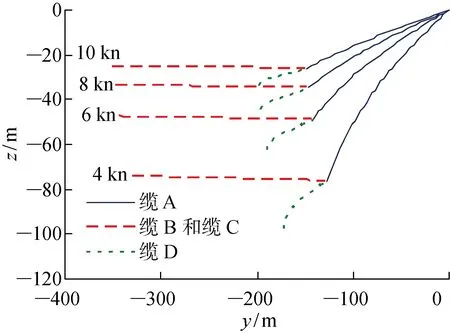
图2 稳态缆形Fig.2 Steady state configurations

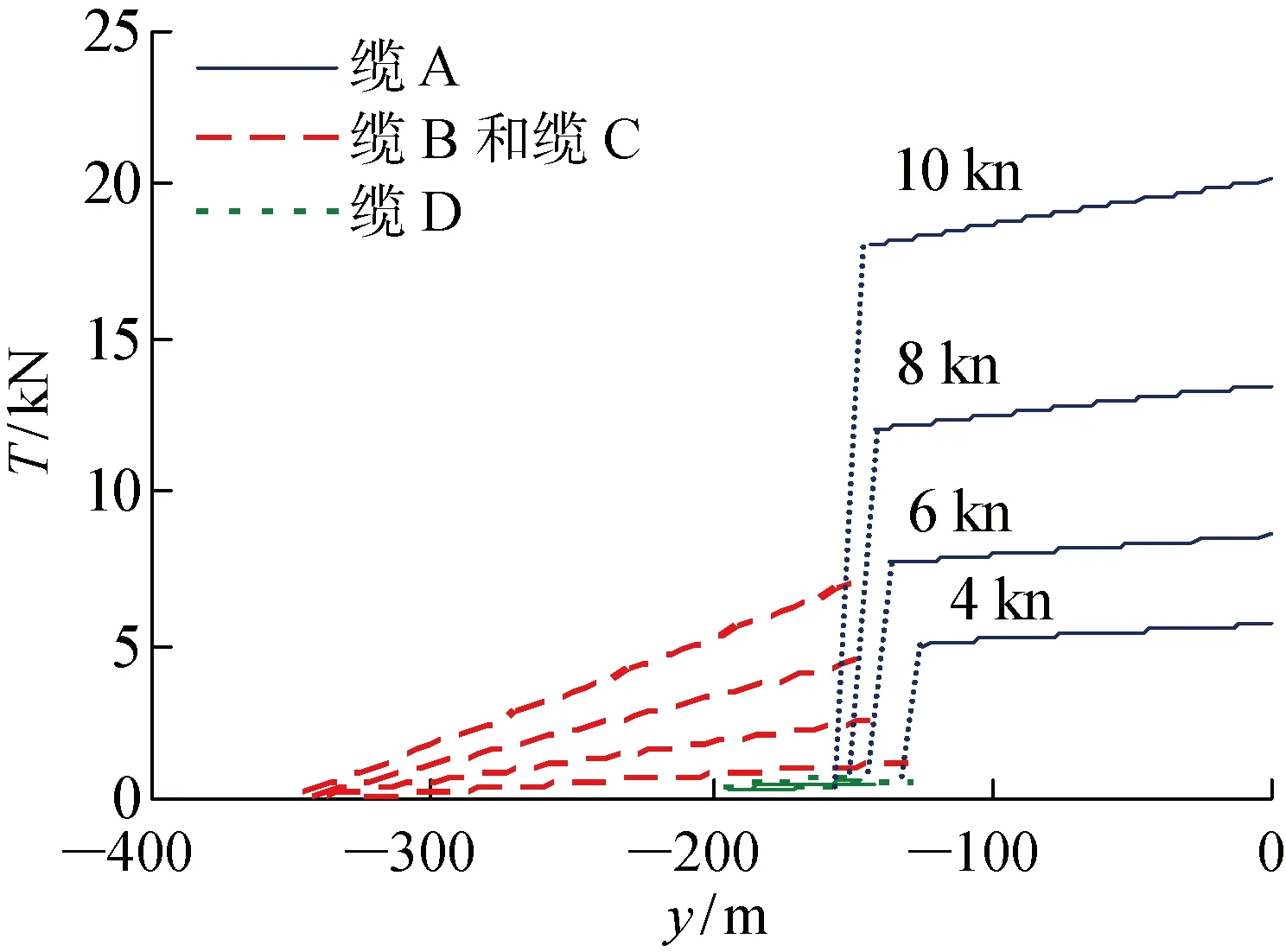
图3 稳态张力分布Fig.3 Steady state tension distribution

结果显示，阵列缆尾端较前端稍有些上浮，因为阵列缆的密度低于水密度，有正浮力.而水下拖体纵倾角由于受到拖体重浮力力矩、水动力纵倾力矩和缆张力形成的力矩多种因素的影响，所以不同速度时变化较复杂，低速时为负值，高速时逐渐增大为正值，且不具有线性关系.

3.2 加速运动计算

加速运动由4 kn加速至10 kn，加速时长分别取为100和400 s.图4所示为牵引缆上端张力变化曲线，图5所示为系统各部位深度变化曲线.由图可见，缆上张力不论加速时间长短，加速过程中逐步增加，在加速过程结束后很快达到稳态，没有出现超调；而拖体和阵列缆在水下的深度，则没能很快地达到稳态，加速时间越短达到稳态的时间越长，特别是零浮力的阵列缆.

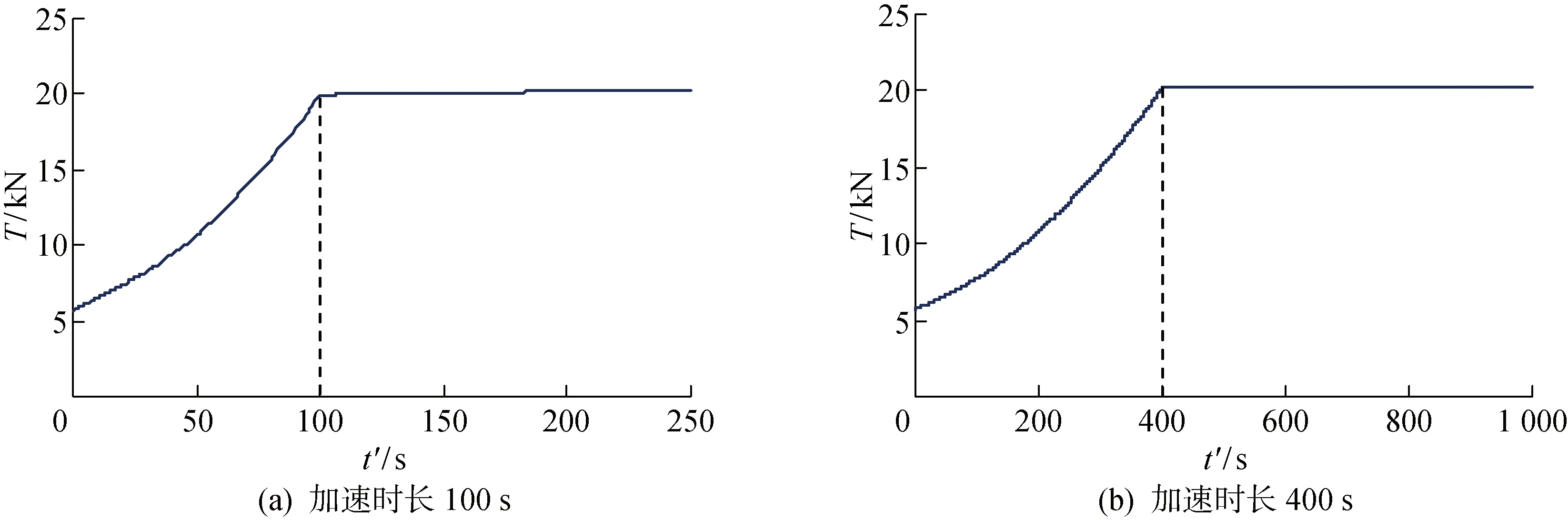
图4 加速运动牵引缆上端张力变化曲线Fig.4 Tension at the lead-in cable upper end for acceleration motion

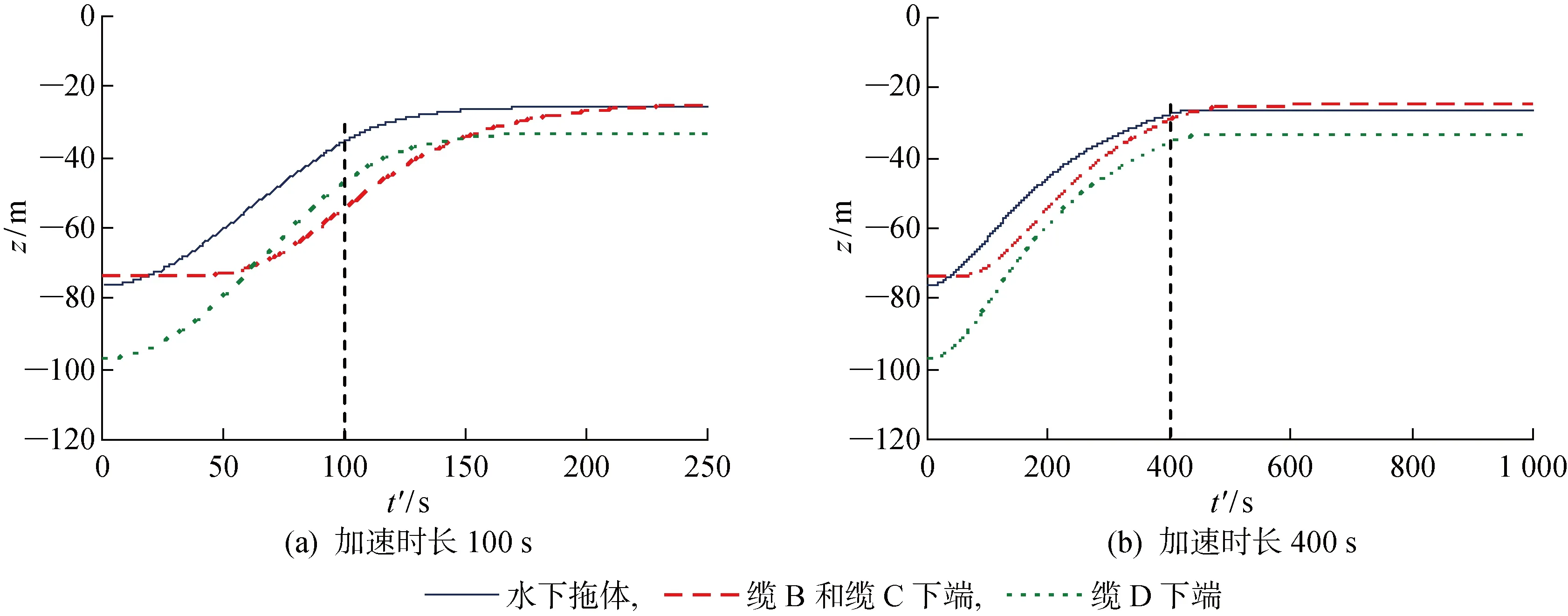
图5 加速运动系统深度变化曲线Fig.5 Depth of the towed system for acceleration motion

3.3 回转运动计算

拖曳系统作360° 匀速回转，然后继续沿原方向直线航行，计算参数为：回转半径取R=100,200 m；回转速度取v=10 kn.图6所示为回转过程中系统的响应曲线，包括拖体深度、拖体横倾角、纵倾角及缆张力的变化， 图7所示为各参考位置的轨迹历时曲线.

结果显示：两个水听器阵列缆尽管间距很小，但回转中始终接近平行运行，无交叉缠绕现象.拖体回转过程中在水下的深度有较大幅度变化，特别是小半径回转时，深度由初始时26 m降低至47.6 m，增加了83%，如水深有限则可能发生碰撞事故；与此同时缆上的张力大幅降低，拖体的横、纵倾角也有较大幅度变化，且有一定的冲击变化现象； 同时系统上的各参考位置，其回转半径均小于拖船的回转半径，特别是阵列缆尾部，回转半径越小减小幅度越厉害，此时阵列缆有可能和牵引缆碰撞或缠绕，导致系统不能正常工作.经仔细计算观测，在R=100 m，t=144 s 左右时阵列缆末端同牵引缆之间的点线距离已接近于零，碰撞缠绕现象可能已发生.

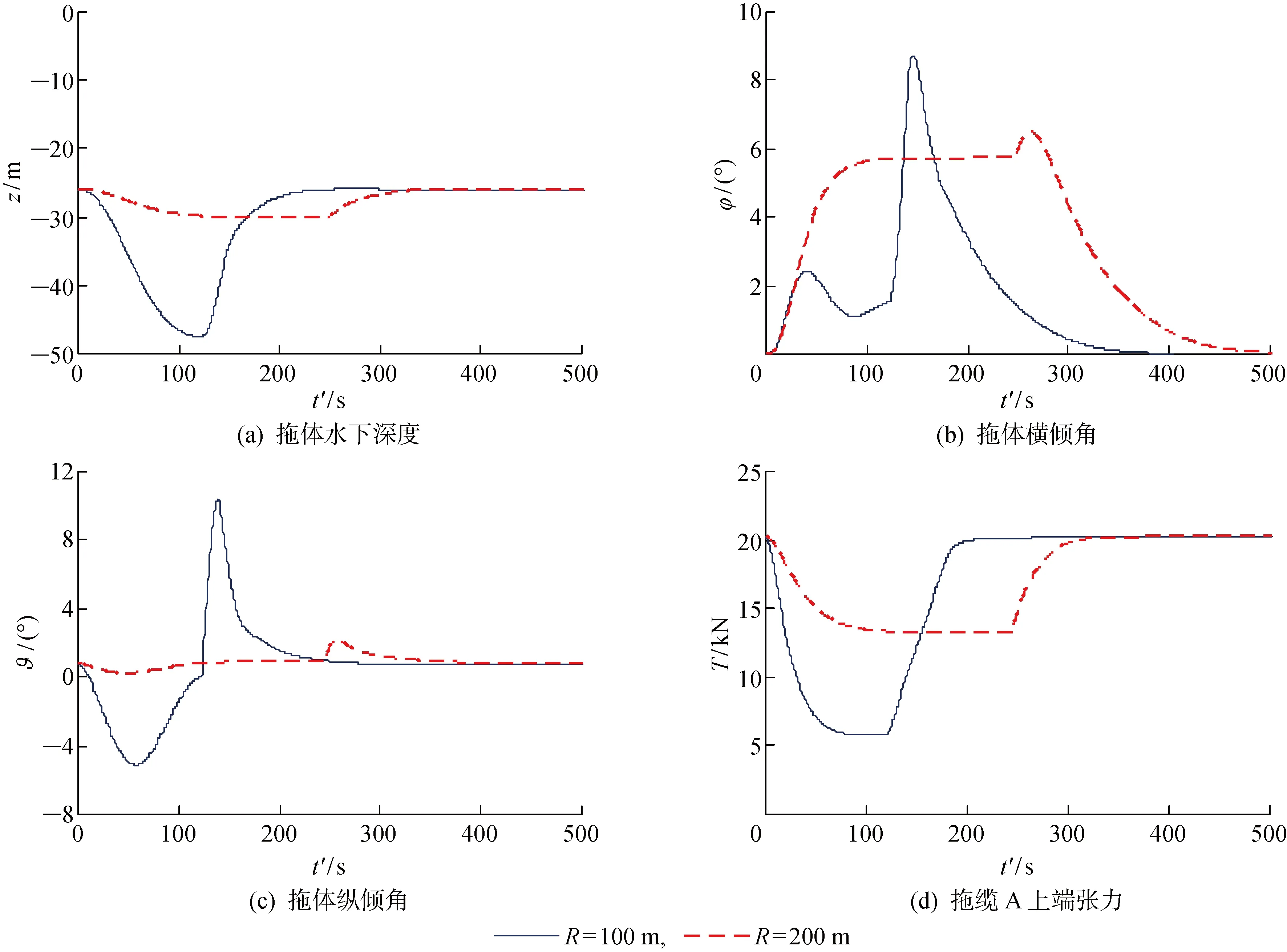
图6 拖曳系统回转运动响应曲线Fig.6 Dynamic response of the towed system during loop maneuver

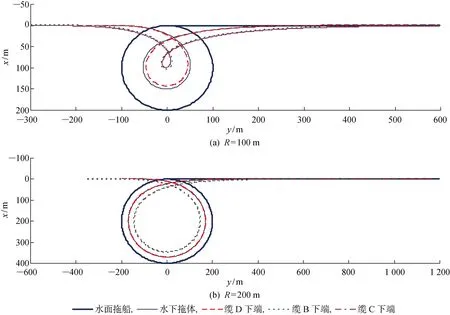
图7 系统回转轨迹曲线Fig.7 Trajectory of the towed system during loop maneuver

3.4 水面拖船振荡响应计算

分别考虑3个方向上拖船振荡(横荡、纵荡、垂荡)对于系统的影响，幅值取为0.5 m，周期为10 s；拖曳速度为v=4,10 kn.图8～10给出了稳定后(t′>800 s)，系统各参考位置处偏荡历时曲线，图中Δx,Δy,Δz为各个方向上的偏荡变化量； 其中横荡时拖船处(缆A上端)张力由于几乎没有变化而没有在图中给出，缆C的结果同缆B全都类似，也没有给出.

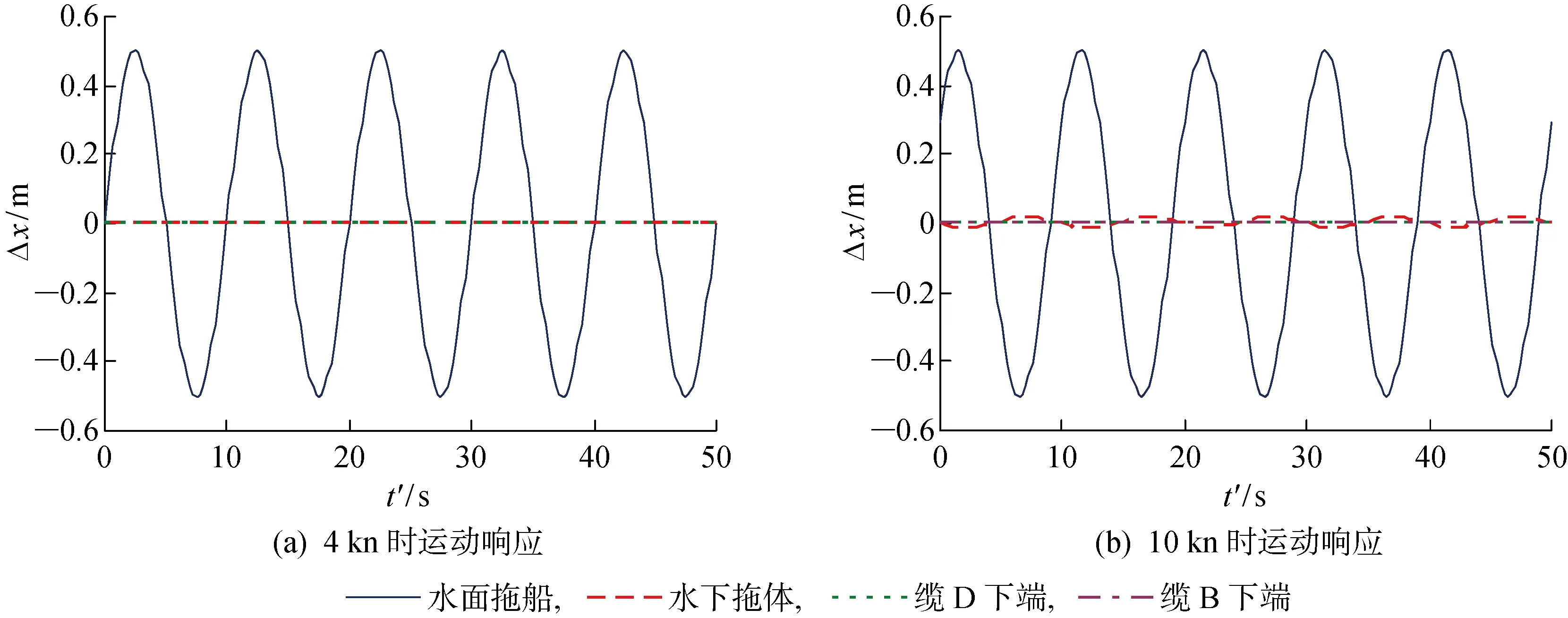
图8 横荡运动响应Fig.8 Response for sway motion

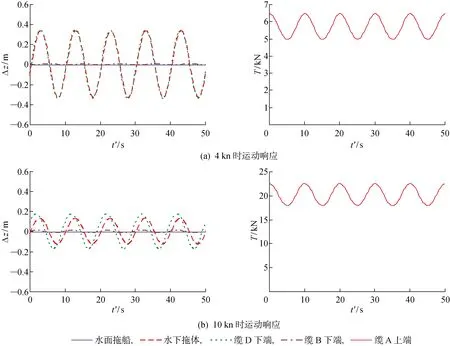
图9 纵荡运动响应Fig.9 Response for surge motion

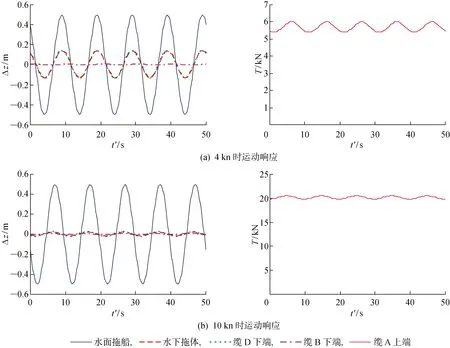
图10 垂荡运动响应Fig.10 Response for heave motion

结果表明，拖船的横荡运动对于系统的影响很小，拖缆张力几乎没有变化，各参考位置的横荡幅度也极小，可以忽略.但是纵荡和垂荡运动对于整个系统有着显著的影响，拖缆张力及各参考位置的深度均有较大幅度的波动，同时结果显示，随着拖曳速度的增加，纵荡和垂荡运动的影响程度会逐渐减小(参考位置偏荡幅度减小)，但横荡的影响会稍有增大.

4 结语

本文采用数值仿真方法，针对水下多缆多体拖曳系统，通过建立其运动数学模型，展开了较为系统的研究，以探讨其在不同情况下的运动响应特性.其中水下拖缆(阵列)采用集中质量法进行建模，水下拖体采用潜艇6自由度运动控制方程，通过建立拖缆和拖体耦合条件以形成整个系统的运动数学模型，采用4阶龙格库塔方法积分求解.最后针对4缆2拖体拖曳系统展开数值模拟研究，分析其在不同情况下的稳态和动态运动响应特性，给出了一些规律性结论：

(1) 系统回转时，拖曳深度和缆上张力有大幅度地降低，拖体的横、纵倾角在回转结束时会出现较大的冲击现象，同时发现高速小半径回转为最危险，拖体及阵列缆旋回半径大幅减小，阵列缆可能同牵引缆发生碰撞缠绕现象.

(2) 水面拖船横荡运动对于系统的影响很小，而纵荡和垂荡却对拖曳深度及缆张力有显著影响，其影响程度负相关于航速的变化.