基于改进二次规划算法的X舵智能水下机器人控制分配

李岳明，王小平，张军军，曹 建，张英浩

(1. 哈尔滨工程大学 船舶工程学院，哈尔滨 150001； 2. 中国舰船研究设计中心，武汉 430064)

X型尾舵(下文简称X舵)是分离式舵的一种形式，最先应用于潜艇.1961年美国海军利用“大青花鱼”号潜艇对X舵的可操纵性进行实验，获得的结论为X舵优于十字型尾舵(下文简称十字舵)[1].目前，各国都十分重视开发海洋资源及发展军用水下无人装备，智能水下机器人(AUV)成为了研究热点之一，而X舵AUV比十字舵AUV具有更好的操纵性[2]，因此X舵AUV获得了广泛关注.X舵AUV的产品有法国的A-18D、冰岛的GAVIA、日本的Yumeiruka、沈阳自动化研究所的便携式X舵AUV[3].X舵AUV拥有诸多优点[4]：① 在近水面处舵效更好；② 卡舵时拥有更高的容错性；③ 可控制横滚；④ 在舵面积相同的情况下，X舵比十字舵的转弯半径小.国外研究虽有涉及X舵AUV或潜艇等方面，但对其中的控制分配技术少有提及，因此控制分配技术的研究具有重要的意义.

控制分配是过驱动航行器与冗余控制系统中的一项关键技术，控制分配技术的研究始于20世纪90年代.文献[5]基于转矩可达集提出直接分配法，利用几何优化法直接寻找可行解，但存在计算量较大的问题.文献[6]针对水下机器人提出一种加权伪逆分配法，其计算过程虽然简单有效，但未考虑执行器约束.文献[7]将序列二次规划算法(SQP)用于7km载人潜水器的控制分配，考虑执行器约束，分配精度较高，但同样存在计算复杂的问题.文献[8]针对X舵AUV提出一种基于 L’evy flight理论的控制分配方法，但由于其迭代是随机的，所以计算量同样较大.

AUV的工作环境十分复杂，在其自主作业过程中，对自身状态控制的准确性与稳定性要求较高.复杂的控制分配算法会降低其控制的实时性，从而增加AUV的反应时间.本文基于Lagrange乘子法和序列二次规划算法，以考虑执行器约束、控制分配精度、减少计算量为目标，提出一种改进的适用于X舵AUV的控制分配方法，最后通过仿真试验验证该方法的有效性.

1 X舵AUV的运动控制

1.1 运动控制体系结构

X舵AUV的运动控制方法与十字舵AUV的控制方法基本一致，因此适用于十字舵AUV的运动控制，如比例微分积分(PID)控制、模糊控制、S面控制等方法.X舵AUV在运动控制体系结构中与十字舵AUV的不同之处在于增加了控制分配环节.X舵AUV的运动控制体系如图1所示.在X舵AUV的实际控制分配问题中，虚拟控制指令τ为3×1向量，包含横倾力矩K、纵倾力矩M、偏航力矩N；u为4×1向量，包含各执行机构的输入，分别对应X舵的4个尾舵；r为期望控制目标；y为AUV的运动状态信息.X舵AUV执行机构的个数多于实际要求的自由度个数，因此是一类具有冗余控制特性的航行器.

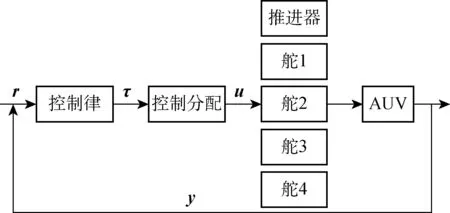
图1 X舵AUV运动控制体系Fig.1 X-rudder AUV motion control architecture

1.2 控制器设计

本文的研究重点是验证控制分配算法的可行性与正确性，因此可选用传统的PID控制.传统的PID控制以其结构简单、稳定性好、工作可靠、调整方便等优点获得了广泛应用.由于研究对象并没有装备垂推与侧推，只有一个主推，AUV通过尾舵产生的偏航力矩与纵倾力矩实现转向与升沉运动，所以对剩余的4个自由度分别设计一个独立的控制器.

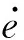
(1)

式中：kP，kI，kD分别为比例项、积分项、微分项的调节系数，不同控制器的参数不同；O为控制输出，在X舵AUV的运动控制过程中，可取K,M,N中的任意项.

对于深度控制，由于需通过改变AUV的纵倾角度来间接实现深度调节，所以不能直接使用深度偏差作为控制输入.使用虚拟变量期望纵倾角θd与实际纵倾角θ的偏差来代替深度偏差作为控制输入，θd可通过下式获得：

(2)

式中：zd为AUV的期望目标深度；sat1(·)为饱和函数；z为AUV的实际深度；C为常数，其值可由不同AUV模型及实际工作任务而定.获得期望纵倾角后，进而可以获得角度偏差eθ=θd-θ，将eθ带入式(1)可获得控制输出.进一步通过控制AUV的纵倾角度，就可实现对于AUV的深度控制.

2 X舵AUV控制分配的数学模型

2.1 控制分配问题描述

线性控制分配问题一般可表述为如下形式：

(3)

s.t.ul≤u≤ut

式中：B为控制分配效率矩阵；ul与ut为所有执行机构的上下限约束向量.实际输入与期望控制力矩的映射可以用函数f表示，非线性映射关系可以表示为

2.2 X舵AUV的控制分配模型

X舵有4个尾舵，每一个尾舵均可独立偏转，因此其操舵组合灵活.X舵相对于十字舵也有诸多优点[4].X舵AUV的三维模型如图2所示，其X尾舵的配置形式如图3所示.由图3可知，从尾部往艏部看，序号1、2、3、4分别代表AUV尾部的4个舵叶，每一个舵叶都有一个单独的舵机与之相连，舵与舵之间的夹角为90°，每个舵与水平轴及其垂直轴的夹角大小均为45°.根据文献[2]的研究结果，45° X舵潜艇的水动力性能较为优良，而X舵AUV可看成是缩小版的X舵潜艇.

图2 X舵AUV的三维模型Fig.2 Three dimensional model of X-rudder AUV

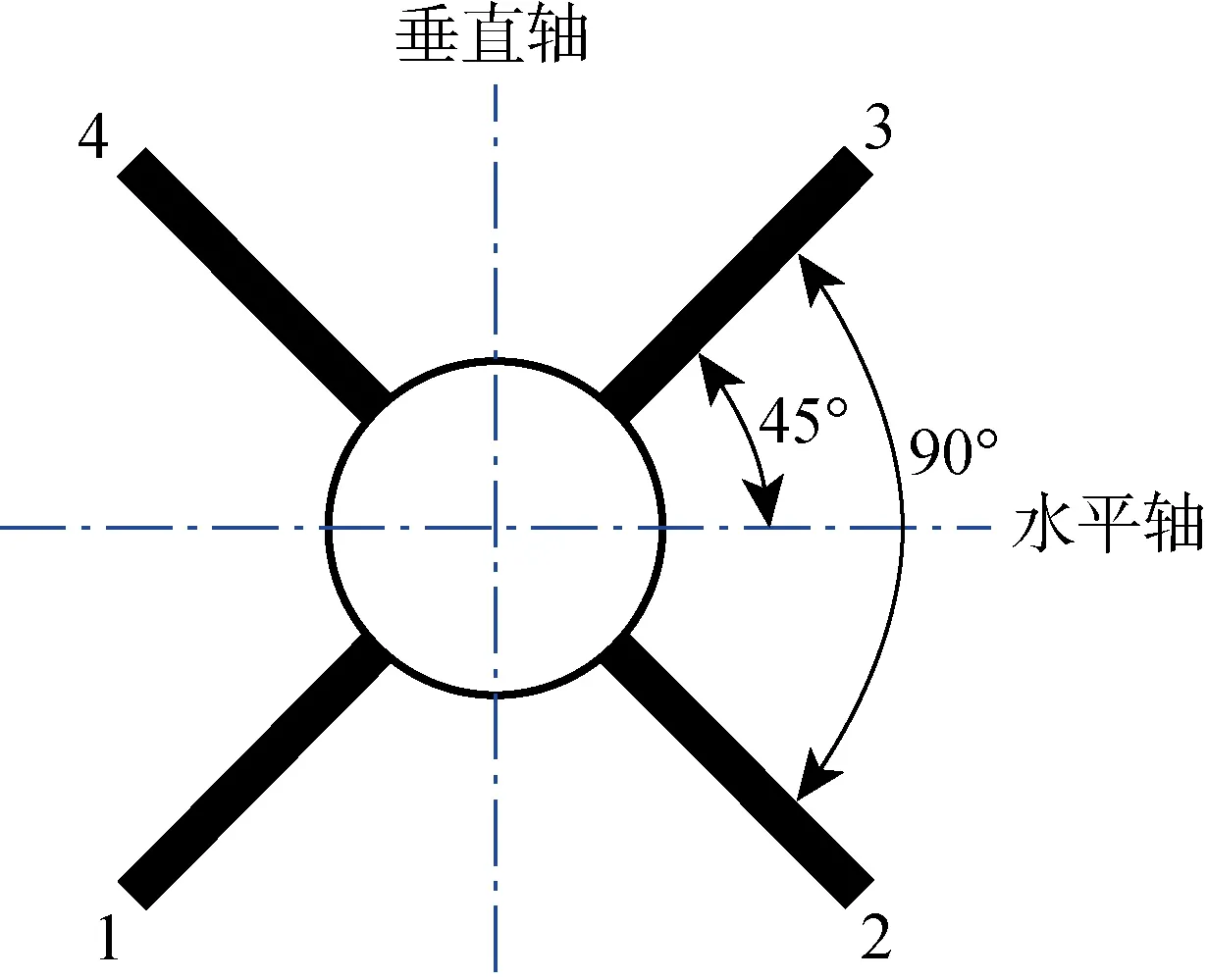
图3 X尾舵的配置形式Fig.3 Configuration form of X tail rudder

X舵AUV的工作环境及其分配环境比较复杂，为了减小复杂度，在保证模型合理的前提下，做出如下假设：

(1) 从虚拟指令到执行机构的输出映射均为线性；

(2) 每个舵的材料、表面平滑度、尺寸完全一样；

(3) 不考虑舵与机器人本身以及舵与舵之间的耦合.

将问题线性化后，可获得B.对于具体的某型X舵AUV，B与AUV的速度、尾舵等参数相关，可表示为

(4)

式中：v为AUV的速度；ki(i=1,2,3,4)为X舵AUV舵叶的横倾力矩系数；mi为舵叶的纵倾力矩系数；ni为舵叶的偏航力矩系数.这些系数可以通过专业的流体计算软件计算并加以处理获得.

AUV的总力矩τ=[KMN]T，u=[u1u2u3u4]T，ui(i=1,2,3,4)分别对应每一个舵叶的指令输入，即需要偏转的舵角大小.则式(3)可表示为

(5)

X舵AUV的控制分配问题，简单而言就是通过已知的τ，求解未知的u.

3 X舵AUV的控制分配

3.1 伪逆法

伪逆(Pi)控制分配是常用的一种控制分配方法，许多的控制分配方法都以伪逆控制分配为基础进行开发.伪逆法具有计算量小和易于实现等优点,但未考虑执行机构的饱和 (位置和偏转速率) 约束限制，也不能实现可达集的全覆盖.Bordignon等[9]通过F-18 High Alpha Research Vehicle (HARV)实验得出伪逆法只可实现可达集中的部分虚拟指令，最好的情况也只能达到其中的42.7%.

本文所提的伪逆是Moore-Penrose逆矩阵，可以通过证明[10]验证矩阵的伪逆是唯一的，欠定方程组的伪逆解即是最小范数解，是方程组的一个可行解，可表示为

u=BT(BBT)-1τ=B+τ

(6)

式中：B+为B的伪逆矩阵.通过伪逆法求出的解有时会超出执行机构的约束限制，所获得的结果一般也不是最优解.对于多目标优化求解问题，常采用非线性规划方法进行求解，例如序列二次规划算法.

3.2 改进二次规划控制分配算法

SQP是求解约束问题最有效的方法之一[11]，其基本思想为每一步迭代均通过求解一个二次规划子问题来确立一个下降方向，以减少价值函数获取步长，重复这些步骤直到求得原问题的解.引用一种基于Lagrange函数Hesse矩阵的SQP,在原方法的基础上改进X舵AUV的控制分配，用以求解控制分配约束的优化问题.

二次规划思想中需要求解的问题可以用如下的通用方程组表示：

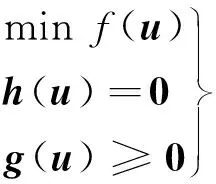
(7)

式中：f(u)为目标优化函数；h(u)为等式约束函数；g(u)为不等式约束函数.针对以上问题求解，首先构建Lagrange函数

L(x,μ,λ)=f(x)-μTh(x)-λTg(x)

(8)

式中：μ，λ分别为等式约束与不等式约束对应的 Lagrange 乘子.再构造二次规划子问题

(9)

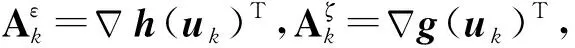
(1) 求解ϖ，方法如下：

ϖk+1=ϖk-σkh(xk)

(10)

式中：σ为系数乘子.若‖h(uk+1)‖≥‖h(uk)‖，则修改σk+1=ησk，其中η∈(0,1)为系数乘子，σk=2，h(uk)为等式约束函数对应的uk值，这里应用了类似梯度下降法求解ϖ.

(2) 求解d，将式(9)转化为

(11)

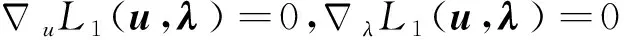
(12)

式中：方程左边的系数矩阵为Lagrange矩阵；a为等式约束h(uk)中的系数矩阵.

定理1设Bk∈Rn×n对称正定，a行满秩.若在式(9)的解d*满足二阶充分条件，即

(13)

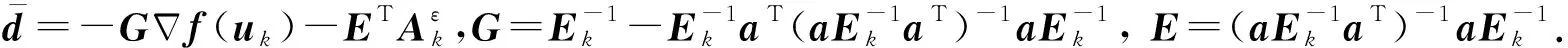
对于式(9)中的不等式约束限制，设立一个饱和函数sat2()来考虑，表达式为

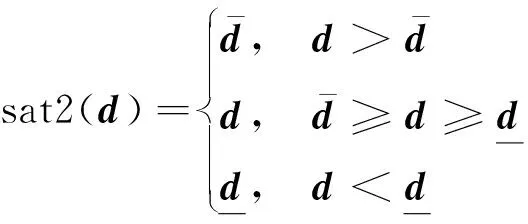
(14)

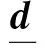
改进二次规划算法(IQP)计算步骤如下：

步骤1指定u初始迭代点u0=[0 0 0 0]T.

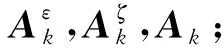
步骤3用改进的算法求解子问题，获得dk,ϖ.

步骤4判断，若‖dk‖1≤β1且 ‖hk‖+‖(gk)-‖1≤β2，停止计算，输出解uk；否则，进入步骤5.

步骤5选择某种价值函数fv，设jk为满足下式的最小正整数j，则有

令αk=ρjk，uk+1=uk+αkdk.

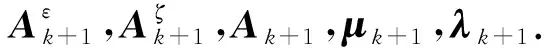
步骤7更新Ek，k=k+1，转步骤3.

4 控制分配算法验证及其仿真分析

4.1 控制分配方法静态对比实验

为了验证IQP的快速性，不考虑AUV的运动控制模型，只考虑一个优化求解问题，目标函数、约束函数如式(13)所示.将改进二次规划算法的计算时间与序列二次规划算法的计算时间进行对比，参考文献[12]中的舵升力解析模型建立方法.当AUV的运动速度为1 m/s时，计算所得的控制分配效率矩阵参数如表1所示；SQP与IQP的计算结果对比如表2所示，其中：eK为横倾力矩误差；eM为纵倾力矩误差；eN为偏航力矩误差；t为计算时间.

表1 控制分配效率矩阵参数Tab.1 Parameters of control allocation efficiency matrix

表2 SQP与IQP的计算结果对比Tab.2 Comparison of SQP and IQP calculations

由表2可知，IQP减少了40%的计算时间，而分配结果误差与SQP相当.

4.2 X舵AUV控制分配方法的动态对比实验

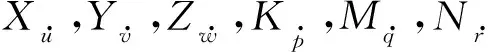
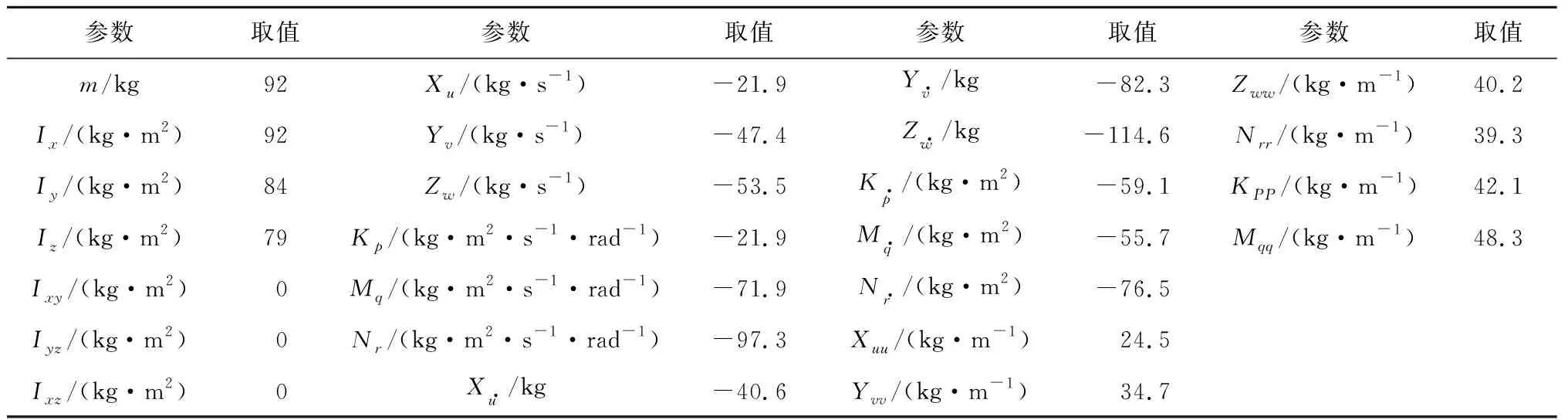
表3 运动模型参数Tab.3 Parameters of motion model

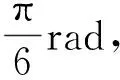
minf=

(1-ϑ)uTw1u+ϑ(τ-Bu)Tw2(τ-Bu)

(13)

等式约束：τ=Bu

式中：w1，w2为单位对角权值矩阵，通过调节其大小可改变对应舵的使用率及优先使用权；ϑ=0.5,为能源消耗问题与分配精确问题的权重；ul=[-30°,-30°,-30°,-30°]T和ut=[30°,30°,30°,30°]T.

将Pi与IQP的控制分配结果进行对比， AUV的纵向速度、深度、艏向角以及横倾角的仿真控制曲线如图4～7所示.其中，ψ为艏向角；φ为横倾角.由于Pi分配结果在t=3 s时超出舵位置偏转约束，所以采用Pi控制分配的结果比IQP更晚达到稳定状态，且采用IQP的AUV姿态控制的效果更好.

X舵AUV采用两种控制分配算法获得的各个尾舵执行的偏转角度曲线如图8～11所示.

X舵AUV采用两种控制分配算法获得的实际横倾力矩、纵倾力矩、转艏力矩与对应3个自由度的期望力矩的分配误差曲线如图12～14所示.

从图4～7可以看出，X舵AUV的艏向、轴向速度、深度在经过一定时间的控制调整后都稳定在了设定值.对于设定的X舵舵角的位置偏转约束[-30°,30°],当t=3 s时，显示Pi控制分配在舵1的分配上超出了约束限制(见图8)，此时Pi控制分配的结果与AUV实际的执行器输出会产生较大的误差(见图12～14).相对的，IQP分配角度曲线没有超出约束，对于Pi控制分配超出约束部分，IQP将其分配到了其余的3个舵上，且K与N的分配误差较小，可以忽略不计，而M的分配误差相对较大，但仍小于分配舵角值的1%，故是优化算法计算时做出的取舍结果.从计算时间、分配误差以及分配结果来看，仿真结果都证明了IQP的有效性与可行性.

图4 AUV的纵向速度曲线Fig.4 Longitudinal speed curves of AUV

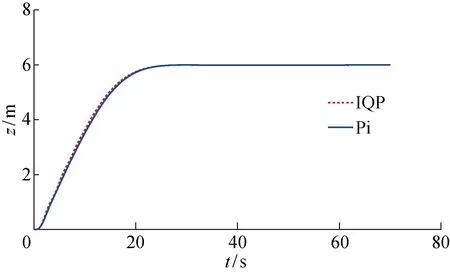
图5 AUV的深度曲线Fig.5 Depth curves of AUV

图6 AUV的艏向角曲线Fig.6 Yaw curves of AUV

图7 AUV的横倾角曲线Fig.7 Rolling angle curves of AUV

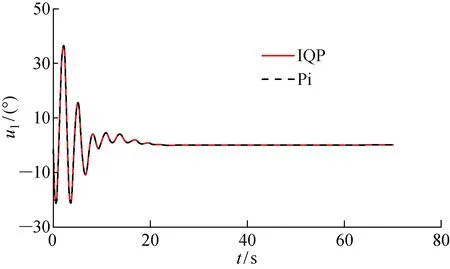
图8 舵1偏转角度曲线Fig.8 Deflecting angle curves of Rudder 1

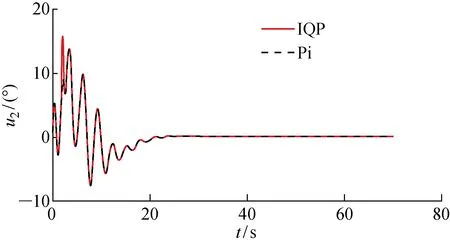
图9 舵2偏转角度曲线Fig.9 Deflecting angle curves of Rudder 2

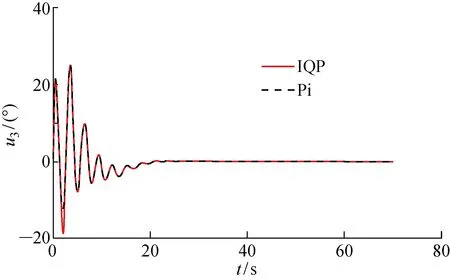
图10 舵3偏转角度曲线Fig.10 Deflecting angle curves of Rudder 4

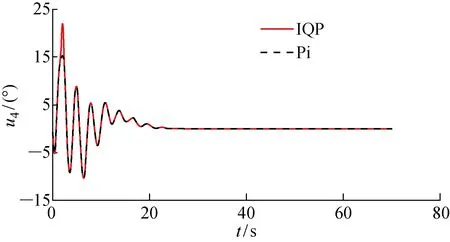
图11 舵4偏转角度曲线Fig.11 Deflecting angle curves of Rudder 4

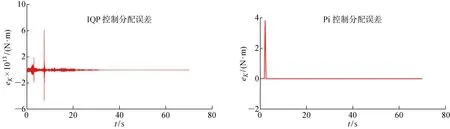
图12 横倾力矩分配误差对比Fig.12 Comparison of rolling torque allocation errors

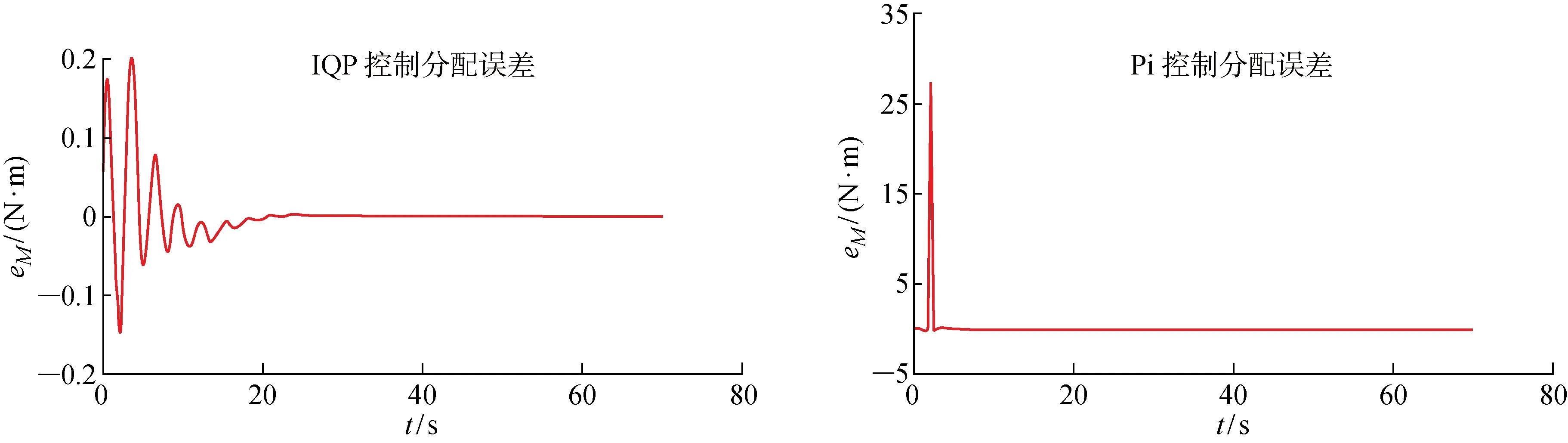
图13 纵倾力矩分配误差对比Fig.13 Comparison of pitch torque allocation errors

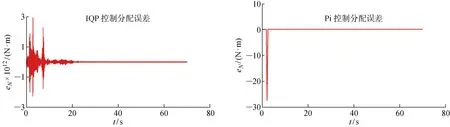
图14 偏航力矩分配误差对比Fig.14 Comparison of yaw torque allocation errors

5 结语

针对X舵AUV的姿态控制分配问题，采用序列二次规划方法，实现了执行器输出范围约束条件下的准确分配.为了改善序列二次规划求解的计算效率，采用Lagrange乘子法替代光滑牛顿法.仿真试验结果表明，改进的序列二次规划方法有效地提高了控制分配的计算效率，保证了控制分配的精度，AUV姿态控制效果满足作业任务需求.另外，所提方法基于约束函数的梯度计算可行下降方向，因此该算法同样适用于非线性约束的控制分配模型.