基于随机矩阵理论的电网事件监测研究

邓子晗，安 军

(东北电力大学电气工程学院，吉林 吉林 132012)

随着电力系统规模的不断发展，电网的动态响应越来越难以预见，若不能及时对这些响应进行态势感知，会给电力系统的安全运行带来隐患.电力系统的事件监测是电网态势感知研究的主要内容，如何进行快速有效的事件监测是对大规模电力系统实时安全运行分析提出的新的挑战[1-4].

传统的电力系统事件监测方法多归于模型驱动[5-9]，文献[5]利用不同事件对发电机同调特性的影响随着电气距离的变化而变化，提出了一种基于电气距离的事件监测方法.文献[9]通过李雅普诺夫方程，基于状态空间提出一种电力系统事件监测方法.该类方法需要事先确定电网的详细拓扑结构及物理参数，同时，电网运行方式产生的变化对监测结果的准确性有所影响，所以在实际应用中，基于模型驱动的方法有一定困难.

数据驱动的方法不依赖于具体模型，也不受运行方式改变的影响.同时，随着以广域量测系统为代表的多种数据采集装置的广泛应用，电气数据的测量维度和采集精度获得了巨大的提升，为事件监测提供了良好的数据基础，启发人们开始对于利用数据分析取代机理建模的相关思考，从而提出了数据驱动的分析模式.随机矩阵理论(Random Matrix Theory，RMT)是近年来兴起的对高维复杂系统进行统计分析的在线大数据分析方法之一.近年来，在金融[10-11]、物理[12]和通信[13]领域取得了一定的成果.随机矩阵理论已经在电力系统进行了初步的应用[14-20]，文献[14]建立一种基于RMT的电力系统大数据应用架构，提出平均谱半径(Mean Spectral Radius，MSR)作为指标应用于电力系统分析研究；在此基础上，文献[15]提出基于高维随机矩阵的WAMS量测大数据建模与分析方法；文献[19]提出一种基于数据相关性分析的故障时刻确定方法.经过大量实际算例表明，上述方法在数据质量较差情况下均难以进行有效检测，如何在噪声环境下进行有效事件监测成为关键.

本文基于随机矩阵理论，根据事件发生后与正常状态下随机矩阵特征值分布所呈现出的不同特征，进行电力系统事件监测.首先研究基于随机矩阵理论的数据模型构建方法；其次利用最大最小特征值极限分布以及特征值均值的能量特征定义一种全新的指标应用于电网事件监测中，对噪声具有一定的鲁棒性.最后通过IEEE39节点算例，与传统MSR方法分析结果相比较，验证方法有效性.

1 随机矩阵理论

1.1 随机矩阵理论概述

一个大维矩阵，若其所有元素均为随机变量，则可称其为随机矩阵.在随机矩阵的行数和列数趋于无穷大且行列比值保持恒定时，随机矩阵的特征值、奇异值以及其他相关参数的统计分布满足一定的特性.随机矩阵的经验谱分布函数是矩阵研究中常用的概念，对于一个n×n阶的矩阵A，它的经验谱分布函数为：

(1)

经验谱分布函数的极限称为极限谱分布函数，通常经验谱分布函数是随机的，但极限谱分布函数具有许多良好的数学性质.

1.2 M-P率和单环定理

利用随机矩阵理论进行电力系统事件监测，是根据随机矩阵在不同情况下谱分布特性的变化规律来评估.它主要涉及两个重要定律，即M-P定律(Marchenko-Pastur law)[20]与单环定律 (Ring Law).

假设X={xi，j}为一个N×T维非Hermitian随机矩阵，该矩阵中元素满足独立同分布的规律，且元素的期望和方差分别满足μ=0，σ2=1.当N，T→且c=N/T∈(0，1]时，即N与T在同一数量级上时，那么样本极限谱密度分布函数f(λsN) 由随机矩阵X的样本协方差矩阵SN的经验谱概率函数收敛得到，见公式(2).

(2)

单环定律在考虑L个独立标准非Hermitian矩阵Xu，i，定义矩阵乘积Z为

(3)

公式中：Xu，i为矩阵X的奇异值等价形式；U为酉矩阵.利用酉矩阵将特征值映射到复平面，其中元素均为独立同分布并且满足μ(x)=0，σ2(x)=1.为了简化，本文后续研究将L设置为1.将矩阵Z标准化为Zstd，使其满足σ2(Zi)=1/N，当矩阵行列比值保持恒定时，则Zstd的极限经验谱分布依概率收敛到为式(4)的概率密度谱分布函数.

(4)

公式中：λZ为特征值；d为N/T∈(0，1].根据单环定理，Zstd的特征值在复平面的分布是一个圆环，内环半径为(1-d)L/2，外环半径为1.

满足圆环率和不满足圆环率时效果图如图1所示.

特征值的分布随着系统运行状态的变化而变化，因矩阵的单个特征值由于随机性不能反映这种特性，为了表征这种数据特性，应寻找一个统计量来体现这种数据特性.传统的随机矩阵理论对系统进行事件监测时，采用平均谱半径作为判断指标平均谱半径是随机矩阵一种常用的线性特征值统计量，是矩阵特征值在复平面上距离原点的距离，MSR的定义为

(5)

公式中：rMSR为随机矩阵的平均谱半径；λi为矩阵的N个特征值.根据MSR与内环半径的大小关系，可以判断系统的运行状态，当MSR小于内环半径时，系统处于不正常运行状态[21].

2 高维随机矩阵应用方法

2.1 随机矩阵模型框架构建

在一个电力网络中选取n个节点的量测数据作为空间样本，其中每个节点共有m个状态变量，构成N个变量，即N=n×m.在任意采样时刻Ti，所有节点的量测数据构成一个列向量

(6)

则在一个时间段内，N个列向量在时序下以公式(7)矩阵表现为

X=[x(t1)，x(t2)，…，x(ti)，…]

.

(7)

为了实时对电力网络数据进行分析，这里采用实时滑动时间窗来生成上述矩阵.实时窗口长度为Nw，宽度为Tw，每次进行采样时采取向后平移一个采样点，ti时刻的实时滑动时间窗包含ti时刻的当前数据和(Tw-1)个相邻的历史数据，即

(8)

公式中：Xti为在ti时刻取得的数据列向量.数据窗的选择主要遵循以下原则：在保障计算速度足够快的前提下，包含所有分区的量测量数据(通常选择各检测点的三相电压及其三相电流数据)；同时为了使不同分区的计算结果可以进行对比，需要保证维容比c=N/T相同，本文一般选取为N/T≈0.5.

则在状态评估时间窗内，对系统的N个可测状态参量测量T次，则在截取的时间窗内，所有测量数据均可以组成的具有电网时空特性的N行T列数据为

(9)

2.2 事件监测方法

通过1.2节所示公式求得X的样本协方差矩阵S，此时矩阵S的特征值分布满足M-P率.由RMT的M-P率可知，样本协方差矩阵的特征值分布满足一定特性，当有事件发生时，该分布特性被破坏，其中，最大特征值和最小特征值的差值与特征值均值之比(DMM)将越过正常的统计范围.因此可通过该特性进行电力系统事件监测.

定义其阈值函数为

γ=(1+N/T)2

.

(10)

当DMM≥γ时，可以判定电力系统有事件发生.具体步骤如下：

(1)将各节点量测数据构造为数据源矩阵Xs.

(2)采用滑动窗口技术，确定其窗口宽度Tw，设定采样起始时刻t1，由阈值函数计算阈值γ.

(3)从数据源矩阵Xs中取得N×Tw维的滑动窗口矩阵X.

(4)对X的行向量进行标准化处理，得到标准的非Hermitian矩阵X.

(5)计算矩阵X的样本协方差矩阵Z.

(6)计算样本协方差矩阵Z的特征值，并计算各时刻下特征值最大值与最小的差值再除以特征值均值，作为电网故障检测指标DMM.

(7)判断DMM≥γ是否成立，若成立，则判定电网有事件发生，否则重复步骤(3)—步骤(7).

3 算例分析

为了验证本文所提的电力系统事件监测方法，算例分析在一个IEEE57节点系统和一个IEEEE 39节点系统下.具体设置是：在IEEE57节点系统借助Matpower软件开展负荷跃变测试；在IEEE39节点借助PSASP软件开展短路故障测试.仿真步长为0.01 s，而用于Matlab分析的量测数据是由所生成数据加上随机误差构成，随机误差设置为高斯白噪声.依据本文方法步骤，利用Matlab 2014a软件编制算法程序，通过与传统的平均谱半径分析方法及计算结果的比较，验证本文所提方法的有效性.

3.1 负荷跃变测试

分别在幅值标准差为1%和2%两种高斯白噪声的场景下研究，共计1000个采样时刻，其中各节点有功负荷变化情况如表1所示.

根据前文所提方法，选取所有节点全部时刻的母线电压数据，构成原始数据源矩阵，设置时间窗窗口长度Tw=120，即每个窗口内采集120列数据，其中包括1列当前全部母线电压数据和119列历史全部母线电压数据，因此本文所提两种方法获得的指标变化曲线都是从采样时刻t120开始.按照前文所提方法得到不同幅值噪声下的MSR方法和本文所提DMM方法指标变化图，分别如图2、图3所示.

由图2可以看出，在高斯白噪声幅值标准差为1%时，在t=0-239区间，MSR在一个正常水平波动，在t=240时，MSR开始下降，说明在t=240时，有事件发生，与算例设置相符.在t=719时刻，系统已经恢复至初始水平，当有功负荷增加100 MW时，MSR又一次发生下降，且比增加50 MW更加剧烈，可知负荷变化程度越大，MSR变化程度也越大；在高斯白噪声幅值标准差为2%时，增加100 MW时MSR法仍可检测到事件发生，但由于噪声干扰，检测不到事件发生，说明传统MSR法尽管能检测到数据发生的变化，但不能在噪声环境下进行有效事件监测.

由图3可以看出，在高斯白噪声幅值标准差为1%时，两种负荷变化均可以进行有效检测，说明了本文所提方法在事件监测方面的有效性；在高斯白噪声幅值标准差为2%时，DMM法不仅可以对增加100 MW的负荷波动进行有效监测，还可监测到增加50 MW这一次负荷波动，证明了DMM方法在噪声环境下的有效监测能力.

图2 负荷跃变情况下MSR指标变化图图3 负荷跃变情况下DMM指标变化图

3.2 短路故障测试

在IEEE39节点标准系统中，分别在1%、2%、5%三种不同幅值的高斯白噪声的场景下研究，共计1000个采样时刻，其中采样时刻t1至t299中无异常事件发生，设置从采样时刻t300起节点9母线出发生两相短路，持续0.02 s.

使用本文所提两种方法开展仿真计算，两种指标变化趋势，如图4、图5所示.

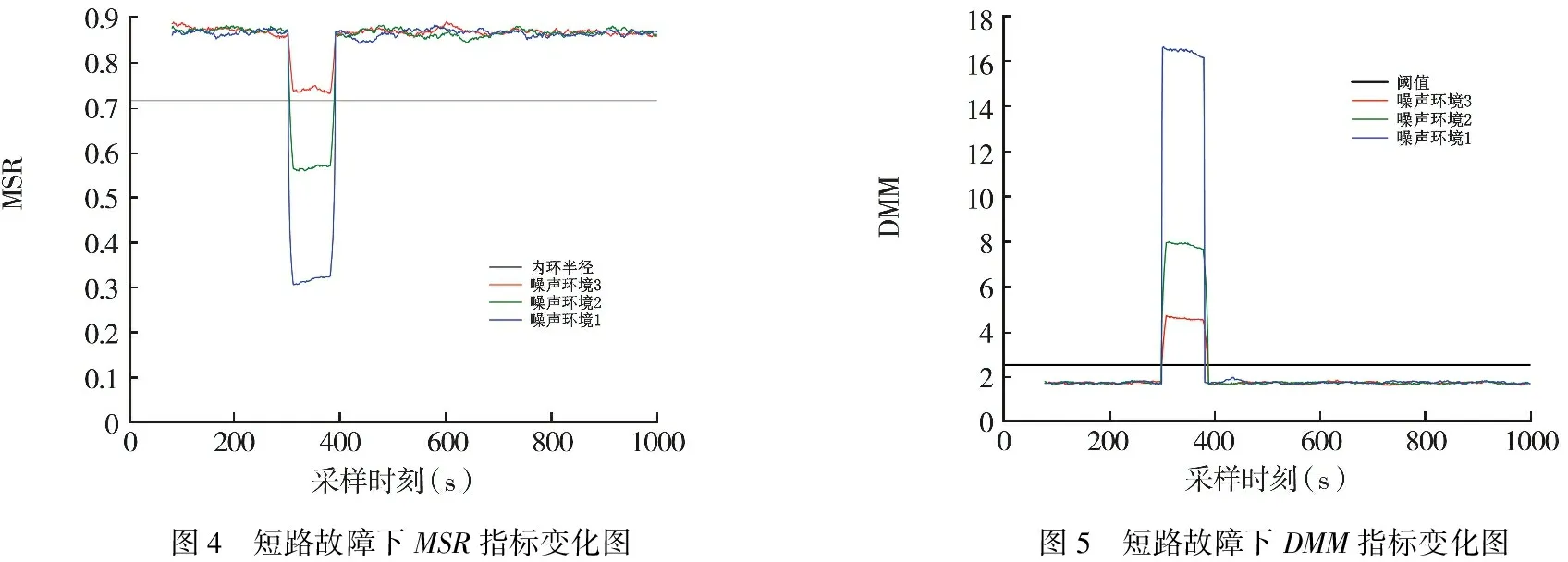
图4 短路故障下MSR指标变化图图5 短路故障下DMM指标变化图

通过对比图4、图5，在噪声幅值较低的环境1和环境2场景下，系统随机性被打破，平均谱半径越过了内环半径，DMM指标也越过了阈值，都可以监测到电力系统事件的发生.在噪声幅值标准差5%的环境3下，由于噪声的干扰，平均谱半径的变化没有越过内环半径，对此次短路故障事件没能进行有效监测，说明该方法在多噪声环境下有一定的局限性；而DMM指标越过了阈值，说明在此幅值噪声下，也可以正常监测到短路故障这一事件的发生.

在不同节点、发生不同类型的短路，添加不同幅值大小的噪声环境下，均进行了测试，本方法较传统MSR法不仅在弱噪声环境下的监测有更大的裕度，在强噪声环境时有更良好的事件监测能力.

4 结 论

本文研究了一种基于随机矩阵理论的电网事件监测方法，通过分析得到以下结论：

(1)基于随机矩阵的电网事件监测方法，在数据驱动模式下可准确确定事件的发生，避免了建模分析的局限性.

(2)相较于传统的MSR分析法，本文所提方法将最大特征值、最小特征值和线性特征值平均值统筹考虑用于事件监测，避免传统分析方法指标进行分析带来的阈值适应性差、抗噪性能差的问题.

(3)所提方法可满足在线实时分析的需要，所构建的在线数据集满足实际在线使用的需要，具有良好的自适应性.

上述结论表明，随机矩阵理论可用于电力系统事件监测，在后续研究中，将对随机矩阵在电力系统态势感知中的应用进行下一步探索.