基于用户感兴趣区域的地理不可区分性的位置扰动算法

罗惠雯，龙士工*

（1. 贵州省公共大数据重点实验室（贵州大学），贵阳550000； 2. 贵州大学计算机科学与技术学院，贵阳550000）

（*通信作者电子邮箱1136297177@qq.com）

0 引言

由于位置服务的普及，个人访问过的位置信息很容易被泄露，其中包括工作住址、喜好、运动模式等，攻击者甚至能够从中提取到关于用户生活习惯、健康状况等极其敏感的信息［1-3］。

目前较为流行的引入到位置隐私保护领域的技术主要是差分隐私［4-6］，其应用随机机制加入受控噪声，在数据发布中，已被证明是有效的。一些有关位置数据隐私保护的研究工作，主要将差分隐私直接应用到位置数据发布中。文献［7］提出了一种利用区域四叉树结构的空间分解技术，提供基于密度聚类算法的差分隐私保护。文献［8］则创建了一个多层的位置信息树模型，利用树型结构结合用户的签到次数来分配隐私预算。文献［9］将差分隐私与隐匿空间技术结合起来，对攻击者的攻击能力进行量化，限制了攻击的成功率。文献［10］证明了位置扰动机制是如何在隐私保护与其所提供服务的准确性之间进行权衡的。文献［11］提出一种基于差分隐私机制的位置数据发布模型。

如果直接将差分隐私应用到位置数据发布中，会存在以下问题［2-3］:首先，当直接利用差分隐私机制来保护位置信息时，由于位置数据集稀疏性的特点，则需要在查询返回值中加入较大的噪声量；其次，对于位置数据集，由于其敏感度［2］的测量与距离有关，如果运用传统的差分隐私方法来计算敏感度，会涉及到位置点间的最大距离，其对应的敏感度也会相对较大；再次，传统的差分隐私适合发布敏感度较小的聚合查询，但对于一组位置点几何质心的发布而言，改变单个位置点可能会极大影响其质心的位置。

3 满足地理不可区分性的位置数据清洗算法

3.1 机制的检索区域

定理2 设检索区域是一个以O为圆心、直径为dA的圆形区域A。给定实际位置x∈A，如果生成的近似位置落在区域A外，则重新在A∩G中生成近似位置，即:

其中:K为满足地理不可区分性的机制，G为笛卡尔网格。如果对用户感兴趣区域内的任意位置t，至少有1-δ的概率，使得检索区域A的圆心O=K(t)满足:

当扰动机制K满足式（9）时，则机制K满足(∂，δ)-效用［12］。

3.2 针对感兴趣区域位置数据的清洗

以用户实际位置x为圆心，假设用户感兴趣区域（Region Of Interest，ROI）的半径为rI。一方面，当机制生成的近似位置位于ROI 范围以内时，机制对服务器反馈的位置信息进行清洗，只将ROI范围内的信息呈现给用户；另一方面，如果生成的近似位置z落在感兴趣区域以外时，仍然将该近似位置作为报告点，可能会造成反馈给用户的查询结果与其感兴趣区域内的实际位置信息偏差较大。针对上述问题，提出基于用户感兴趣区域的地理不可区分性扰动方法，对位置数据进行清洗。

定理3 设ROI 的半径为rI，当d(x，z)＞rI时，报告位置点M为:

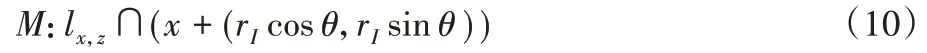
式（10）表示将z投影到rI的边界上，取x与z所在直线lx，z与感兴趣区域边界的交点M作为报告位置点，来代替近似位置z，如图2所示。图2展示了以x=(0，0)为中心，ε=1.25时的平面拉普拉斯概率密度函数，其中，d(x，z)=1.29，取rI=0.8。

图2 投影近似位置到感兴趣区域边界Fig. 2 Mapping approximate locations to boundary of ROI

下面将证明该方法的可用性。

3.3 算法描述

根据实际位置坐标提供l/r-地理不可区分性。首先为了实现ε-地理不可区分性的隐私保护水平，算法通过调整隐私参数ε，来确保其所需的可用性程度。对于用户的实际位置，采用扰动机制画出半径r和角度θ。然后，在指定区域内，通过对真实位置添加噪声(r，θ)，生成近似位置z。如果z落在感兴趣区域外时，将x投影到感兴趣区域的边界上，得到投影点M并报告该点。最后，对近似位置添加噪声(r0，θ)，得到检索区域A的圆心O。动态调整O的位置，使半径为r的保护区域范围内任一个近似位置z都在检索区域内的概率至少为1-δ。

结合上述内容，基于用户感兴趣区域的地理不可区分性（Geo-indistinguishability based on the Region Of Interest，GROI）的扰动算法如算法1所示。

3.4 查询结果定量分析

经过扰动后的位置数据主要用来进行地图查询。对各检索范围的位置数据进行统计，将真实位置的查询结果分别与ε-地理不可区分性算法及本文算法的查询结果进行对比。

本文涉及的查询主要分两种情况:

1）对实际位置点x生成的近似位置zi∈ROI。根据GROI算法，检索区域A取决于近似位置zi，假设检索区域内包含i个用户想要获取的地理位置点point1，point2，…，pointi，然后统计这些位置点Count(i)←Count[pointi∈A]。

2）生成的近似位置zi∉ROI。结合3.1节的内容，由于检索区域A的圆心位置取决于近似位置，即O←zi+(r0cosθ，r0sinθ)，为了能使A能够包含ROI，对位置点进行清洗后，再执行1）操作。下面对清洗位置点能够提升精确度进行理论分析。

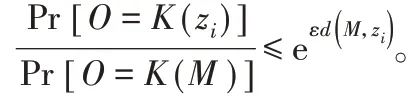
4 实验分析

4.1 检索范围对比分析

实验在谷歌地图查询下进行，设定用户实际位置位于堪萨斯州的国家一次世界大战（World War I，WWI）博物馆内，该用户对博物馆附近900 m 范围内的酒店位置信息进行查询。指定距该博物馆250 m范围以内的区域作为机制的保护范围。

在定理3 保证方法可用性及隐私保护水平的前提下，实验主要从对比查询结果与真实位置数据在不同检索范围内的准确度展开，分析影响查询结果准确度的因素，并在4.3 节的实验中将GROI算法与ε-G算法进行了对比。

本实验共生成4 个改变隐私参数大小的查询:0.1、0.2、0.4、0.6，通过ε-G算法对用户实际位置进行扰动。图3中展示的是不同检索范围内查询结果与真实位置数据的分布对比。

从图3 中能够看出，随着检索范围的扩大，在近似位置得到的查询结果会越来越接近实际位置。但当检索范围减小时，查询的准确程度有所降低。

图3 不同检索范围内实际位置与近似位置对比Fig. 3 Comparison between real location and approximate location with different query ranges

4.2 机制服务质量分析

本实验主要测试影响算法查询结果的因素。采用相对误差（Relative Error，RE）计算查询结果的精确度。设定用户位于堪萨斯州的一家名为Rozzelle Court 的餐厅内，并分别查询了0～0.8 km，及0.8～1.8 km 范围内的餐厅及宾馆位置分布比例如图4 所示。图4（a）展示了当ε= 1 时，改变保护范围，随着可区分性水平l的增大，分布比例的对比情况。图4（b）展示了当r不变时，隐私参数ε分别为0.10、0.50、1.00，随着l增大，在不同检索范围查询结果的位置分布比例情况。

图4 不同隐私水平下的查询对比Fig. 4 Query comparison under different privacy levels

表1展示了与图4（a）相应的误差率对比情况。与真实数据相比，l分别为1.36、6.55 时，查询结果的精确度分别降低了7.0%、15.0%。

表2 展示了图4（b）相应的误差率对比情况。与真实数据相比，l从0.313增大到2.104时，查询结果的精确度降低了9.1%。

表1 ε-G算法相对误差Tab. 1 Relative error of ε-G algorithm

表2 ε-G 算法查询相对误差Tab. 2 Relative error of ε-G algorithm query

4.3 清洗数据前后对比分析

通过以上实验可以发现，ε-G算法对小范围检索结果影响相对较大。基于此，从用户感兴趣区域的角度考虑，当生成的近似位置落在该区域以外时，如果仍然报告该近似位置，会导致查询结果的误差较大。针对上述问题，将用户感兴趣区域作为约束条件，依据GROI算法，对查询结果进行清洗，在隐私程度不降低的情况下，查询结果的位置分布比例如图5所示。可以看出，相比ε-G算法，GROI算法的查询结果更接近真实值。

对比GROI 算法与ε-G 算法的查询结果，在ε=0.2，0.8时，查询结果的相对误差如表3 所示。改变检索范围，尤其是针对近距离范围进行检索时，GROI算法查询结果的精确度比ε-G算法提升了至少2个百分点。

图5 算法查询结果对比Fig. 5 Query result comparison of algorithms

表3 两种算法的查询相对误差对比Tab. 3 Query relative error comparison of two algorithms

根据前面章节，由于ε-G算法与GROI算法均提供εd(x，z)-隐私，所以两者均引入O(|x|3)的隐私约束［13］。下面对两种算法的运行时间进行对比，如表4所示。从表4可以看出，GROI算法根据ROI对数据进行清洗，并没有造成额外的计算开销。

表4 两种算法运行时间对比Tab. 4 Running time comparison of two algorithms

5 结语

本文通过理论分析和实验，证明了基于感兴趣区域的地理不可区分性方法的可用性，并对比了在改变保护区域范围及隐私参数的情况下，扰动算法查询结果精确度的变化。当保护范围的半径固定时，随着可区分性水平的减小，隐私程度增大，查询结果的精确度有所降低，这取决于用户对隐私程度的要求。通过实验发现，地理不可区分性算法查询与真实位置相距较远的位置信息较为准确，而检索小范围内位置信息时，存在一定的误差。基于此，GROI算法将用户的感兴趣区域作为算法的约束条件，对查询结果进行清洗，在隐私保护程度不降低的情况下，进一步减少查询误差。并通过实验结果对比分析，表明了通过数据清洗后得到的结果精确度整体高于地理不可区分性算法。