基于扩展极大值变换沥青混合料数字图像预处理方法研究

曾晟，梁乃兴，薛轲，2，张莹莹

(1.重庆交通大学，重庆市 400074；2.中国市政工程西南设计研究总院有限公司；3.云南省交通规划设计研究院有限公司)

道路工程与数字化新技术相结合用于提高公路的施工和检测效率，尤其是数字图像处理技术的应用，成为现在公路工程热点研究之一。例如运用数字图像技术进行沥青混合料级配检测、集料筛分判别、裂缝检测等。近年来，有学者将数字图像技术应用于沥青路面摊铺均匀性检测，提出了一种新的沥青路面离析实时检测方法。即通过数字图像基础对采集到的二维摊铺沥青路面图像中颗粒进行均匀性评价。其中一个关键环节就是对采集到的图像进行预处理，即将采集到的图像通过计算机软件消除图像中的噪声干扰，提高图像的细节及质量，使图像的真实信息得以恢复，提高检测结果的准确性及真实性。但沥青混合料原始图像通过数字图像处理技术进行灰度化 、空间滤波、直方图均衡化、二值化、形态学处理等数字图像处理后，由于沥青的裹覆，图像中存在部分颗粒黏连的情况，与实际集料颗粒形态不符。为进一步将图像中黏连颗粒分开，需要采用分水岭分割方法(Watershed)对其进行分割，以还原图像集料颗粒的真实形状。传统的图像预处理方法应用在沥青混合料图像预处理时，在二值图像形态学分水岭分割处理中容易出现图像的过度分割，使预处理得到的图像无法反映沥青混合料颗粒的真实分布情况。该文采用基于扩展极大值变换的分水岭算法对二值化处理后的沥青混合料数字图像中黏连颗粒进行分割，为下一步图像分析奠定基础。

1 传统分水岭算法

所谓分水岭算法，是将灰度图像理解成一个拓扑表面，表面中f(x,y)值的大小被视为高度。其基本思想是与测量学中拓扑地貌想结合，地貌中的海拔高度则对应图像中的每一个像素点。在这个拓扑地貌中，极小值区域形成的低凹区称作集水盆，分水岭即为集水盆区域的边界。在集水盆区域的边界，假设通过刺穿一个小孔，并将分水岭地貌模型浸入水中，集水盆区域会随着浸入程度的深入，汇集而形成大坝，即为分水岭。

分水岭算法通过排序和淹没两个过程实现。即首先以低到高的顺序将灰度图像中每个像素对应的灰度级进行排序，再进行淹没操作。

通过分水岭算法得到的集水盆是封闭且连续的，可以保证图像区域特征得到分析，但传统的分水岭算法对图像中噪声和边界细致纹理反应敏感，沥青混合料中集料被沥青裹覆，对于黏连颗粒，图像分割时往往会造成图像的过度分割。

2 基于扩展极大值变换的分水岭算法

通过对传统分水岭算法分割后的二值图像进行欧氏距离变换后得到灰度图像，发现图像部分颗粒内部存在多个极大值点，是导致颗粒过度分割的原因。为了消除过度分割现象，通常有以下两种方法：① 根据经验提前去除无关的边界信息，但是复杂、灵活性差；② 修改梯度函数使影响域只响应目标区域，但是其准确性不高。

秦一博采用扩展极大值变换分水岭算法对黏连玉米颗粒图像进行分割,取得了良好的效果。其引入基于扩展极大值变换的分水岭算法将多个极大值点扩展合并，使得颗粒的局部极大值点唯一存在，从而降低图像过度分割。

数学形态学中有很多关于区域极大值(Regional-maximum)的变换方式，如H极大值(H-maximum)变换、扩展极大值(Extended-maximum)变换等。如图1所示，为极大值变换的示意图。

图1 极大值变换示意图

直观来看，原灰度图像的区域极大值为M，选取阈值为h的变换深度。对于H极大值变换，区域内所有灰度值大于M-h的像素其灰度值变换为M-h，区域内所有灰度值小于M-h的像素其灰度值保持不变；对于扩展极大值变换，区域内所有灰度值大于M-h的像素其灰度值变换为1，区域内所有灰度值小于M-h的像素其灰度值变换为0。

事实上，H极大值变换实现了对所有深度小于阈值h的极大值的抑制，而扩展极大值变换本质上就是H极大值变换后灰度图像对应的区域极大值，经过扩展极大值变换后，灰度图像转化为二值标记图像。

H极大值变换数学表达如式(1)：

(1)

式中：f为原始灰度图像；h为设定的阈值。

扩展极大值EMAX定义为对应于H极大值变换的区域极大值，如式(2)所示：

EMAXh(f)=RMAX[HMAXh(f)]

(2)

3 工程实例

依托云南玉溪至楚雄高速公路工程建设项目，从下面层AC-25型沥青混合料摊铺施工时采集照片。

沥青路面图像的预处理包括3个方面：图像有效目标的提取、图像的二值化处理及图像的分水岭分割。

3.1 图像有效目标提取

为了提取沥青路面图像中的有效目标方便后续处理计算，首先要将数码相机采集到RGB彩色图像转换为灰度图像。每个像素点的转化公式为：

Gray=0.299R+0.587G+0.114B

(3)

转为灰度图像后基本保留了图像的原有信息，原有物体清晰可见，视觉效果良好。

采集的图像受内部、外界的影响，常常掺杂一些噪声，导致图像质量降低。为了改善图像质量，去除高频噪声干扰，增强影响边缘，还原真实图像，去除模糊，采用中值滤波对图像进行空间滤波处理。

为了进一步增强图像对比度、提升图像清晰度需要对图像进行直方图均衡化。直方图均衡化后的图像动态范围得到扩展，如图2所示。

图2 直方图均衡化处理效果

3.2 图像的二值化

考虑到沥青混合料采集的图像本身呈灰黑色，仅通过灰度转换无法完成后续计算，因此需要进行进一步调整。为了统计集料颗粒在平面上的面积分布情况，需要将灰度图像转化为二值图像，如图3所示。

图3 灰度图二值化对比效果

3.3 小颗粒过滤

玉溪至楚雄高速公路路面为AC-25型沥青混合料下面层。过滤掉对均匀性影响不大的粒径小于9.5 mm的小集料颗粒，便于图像分析。

假设：① 集料颗粒都呈圆形；② 混合料摊铺过程中粒径为9.5 mm的集料颗粒在数字图像上直径所占据的像素为d。

(4)

得到d=32.3≈33；因此，整个粒径为9.5 mm的圆形颗粒所占据的像素大小处于850～900之间，此处取850。过滤9.5 mm以下颗粒后图像如图4所示。

图4 小颗粒过滤效果

3.4 图像的形态学处理

如图4中，二值图像颗粒存在不光滑的“毛刺”，为了对图像进行平衡化，消除图像中的小洞，需要对图像进行形态学处理。在实际应用中，主要利用不同的形态学基本运算，如腐蚀、膨胀、开运算、闭运算的合理组合，对图像进行处理，改善图像质量。

3.5 分水岭分割方法

经过形态学处理后的二值图像，如图5(a)所示，局部放大后可以看到有部分颗粒黏连在一起的情况，如图5(b)所示，对后续颗粒数目统计和静矩计算的准确性造成影响，需要寻找一种有效的方法将黏连的颗粒分割开。

图5 形态学处理后二值图像

为进一步将图像中黏连颗粒分开，需要采用分水岭分割方法(watershed)对其进行分割，以还原图像集料颗粒的真实形状。

(1) 传统分水岭算法

通过传统分水岭分割方法对图像中黏连颗粒进行分割，由于图像中的噪声、物体表面细微的灰度变化，使处理结果产生过度分割的现象，如图6所示。

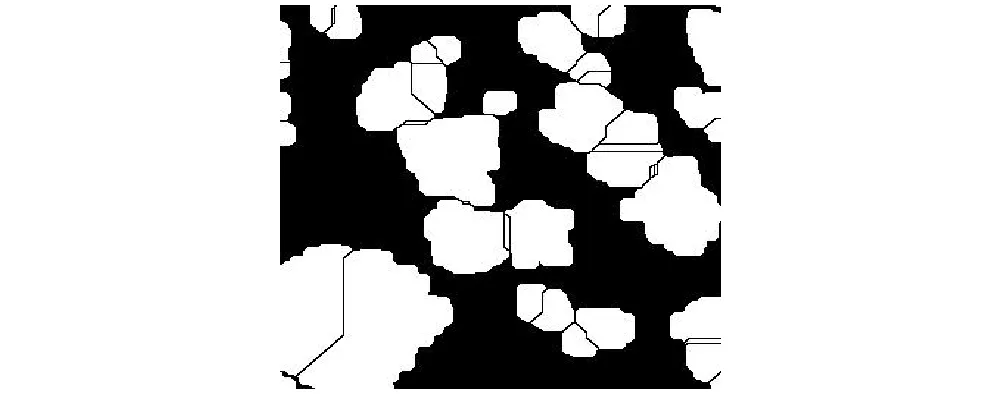
图6 过度分割现象

(2) 基于扩展极大值变换的分水岭算法

基于扩展极大值变换的分水岭算法将多个极大值点扩展合并，使得颗粒的局部极大值点唯一存在，这样会大大消除图像的过度分割，对黏连颗粒图像具有很准确的分割率和很好的适用推广性。

通过对形态学处理后的二值图像采用基于扩展极大值变换的分水岭算法进行黏连颗粒分割，得到局部区域放大后的二值图像，如图7所示。与图6对比，图7中碎片颗粒较少，有效地减少了过度分割现象。

图7 扩展极大值变换后的二值图像

该算法的关键在于确定合适的阈值才能避免过度分割出现，实现对原始图像的正确分割。由于距离变换后的灰度值出现小数，为了提高运算的准确性，采用灰度归一化处理，即距离变换之后的灰度值控制在[0，1]之内，然后逐步增加Δh来确定h的最优取值范围。试验表明：选取阈值h较小时，能够准确统计颗粒的数目，这里设置阈值h=0.1。

3.6 分割结果验证

级配能够反映出集料各级粒径颗粒的分配情况，类似地，定义沥青路面的颗粒面积比A，如式(4)所示，用来描述图像中不同档集料颗粒的面积与沥青路面图像总面积的比值。

(5)

式中：Pi为图像中各档集料每个集料颗粒的像素值；Z为二值图像的行列数。

假设沥青路面集料分布均匀、颗粒形状为圆形，由不同集料密度、质量大致推算出按合成级配各档集料的颗粒面积比。

计算现场采集的1 085张AC-25下面层预处理后图像中9.5 mm以上颗粒平均颗粒面积比，并与合成级配下颗粒面积比进行对比，对图像预处理结果进行验证，结果如表1所示。

表1 9.5 mm筛孔以上颗粒面积比对比结果

由表1可知：通过扩展极大值法预处理得到的二值图像中26.5 mm颗粒面积比与按合成级配计算得到的颗粒面积比相差0.13%、19 mm颗粒面积比相差2.12%、16 mm颗粒面积比相差0.79%、13.2 mm颗粒面积比相差1.58%、9.5 mm颗粒面积比相差0.93%。

并将最终处理形成的二值图像与最初采集的RGB图像相叠加，如图8所示。通过对9.5 mm粒径以上的集料颗粒进行面积统计，其面积所占比例为38.8%，与实际路面较为吻合。

图8 处理前后叠加图

4 结论

数字图像预处理是运用数字图像处理技术的基础。该文通过Matlab软件对沥青混合料数字图像进行预处理，提出了扩展极大值变换的分水岭算法。主要研究结论如下：

(1) 通过对沥青混合料数字图像进行数字图像预处理，得到的二值图像局部出现颗粒黏连情况，需要对其进行分割处理。

(2) 由于图像中噪声、表面灰度变化等因素，传统的分水岭算法会使沥青混合料数字图像出现黏连颗粒的过度分割。

(3) 提出扩展极大值变换的分水岭算法，大大消除了黏连颗粒的过度分割现象。

(4) 将最终处理得到的二值图像与原始沥青混合料图像进行重叠，直观上与实际相符，并通过计算9.5 mm以上集料颗粒的面积，其38.8%的面积占比符合实际规律。因此，采用扩展极大值分水岭算法对沥青混合料数字图像黏连颗粒分割具有良好的效果。