光栅二次分光理论在实验教学中的应用

张明霞，令维军

（天水师范学院 电子信息与电气工程学院，甘肃 天水 741001）

在大学物理光学理论及实验教学中，几何光学和波动光学是非常重要的内容，属于经典光学，三棱镜折射率的测定及光栅衍射实验是必做的基础性分光实验，棱镜和光栅是最基本的分光元件，在分光仪上通过望远镜可观察到棱镜光谱和光栅光谱，但二者的分光机理不同，棱镜光谱是由光的色散作用而形成的一级彩色光谱，以光的实验定律为基础，属于几何光学的范畴，用光的粒子性做出理论解释，而光栅光谱是同时考虑单缝衍射及缝间干涉而形成的多级彩色光谱，以惠更斯原理为基础，属于波动光学的范畴，用光的波动性做出理论解释。

笔者通过多年的光学理论及实验教学发现，在分光仪上做分光实验时，若将复色光先通过棱镜分光，可得到一级彩色光谱，若再通过光栅进行二次分光，可以将棱镜得到的一级彩色光谱转化成多级彩色光谱，即夫琅和费光栅衍射图样，且谱线非常细锐非常明亮。下面以双棱镜为例，先用双棱镜分光，再用平面透射光栅（以下简称光栅）进行二次分光，通过理论分析及推导，得到测量双棱镜的折射率、光波波长及光栅常数的简易方法。

1 双棱镜及光栅的分光光路示意图

图1所示为在分光仪上做分光实验时的分光光路示意图，分光仪是测角度的仪器，先调好分光仪，具体调节方法参照文献[1-3]，然后在分光仪的载物台上依次平行放置双棱镜和光栅，高压汞灯发出复色光通过平行光管，平行光管出射平行光先通过双棱镜分光，再通过光栅进行二次分光，转动望远镜就可观察到两侧对称的彩色光谱线。

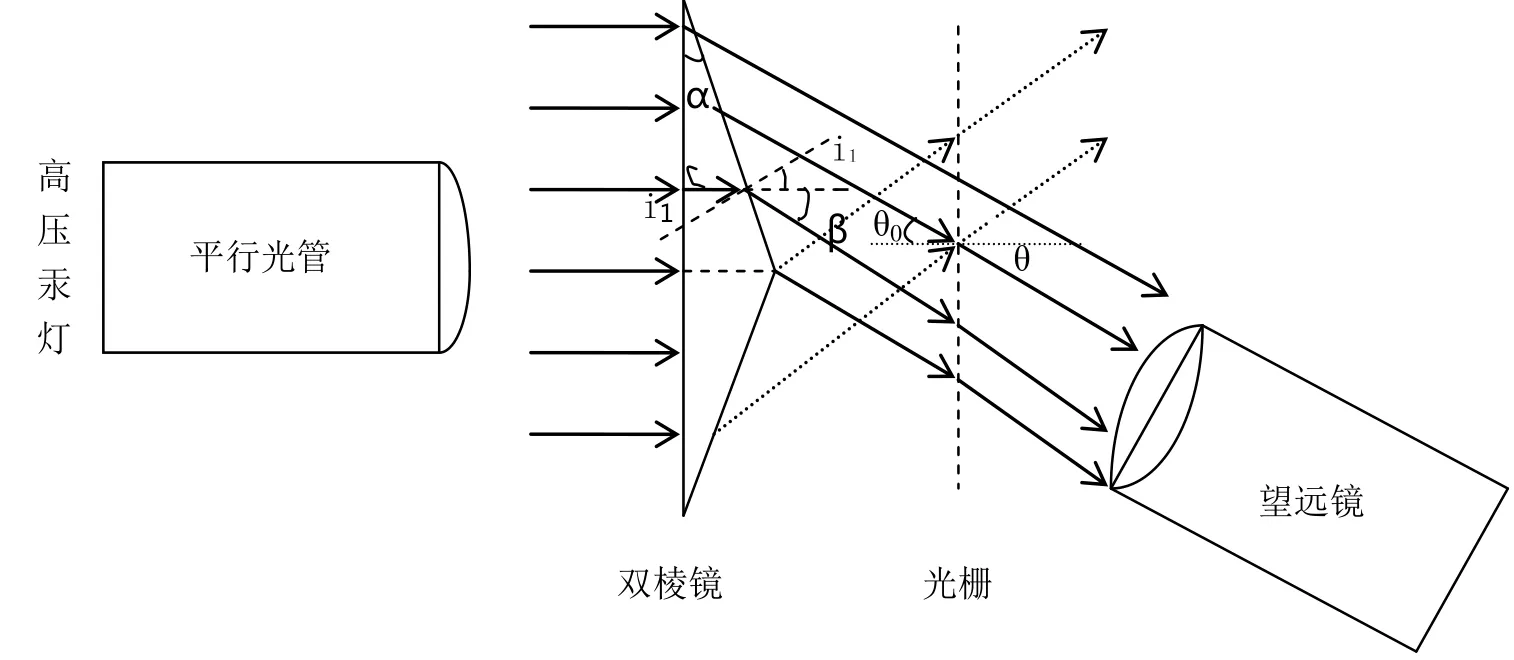
图1 双棱镜及光栅分光光路示意图

2 双棱镜折射率的计算公式推导及测量方法

2.1 双棱镜折射率的计算公式

图1中，双棱镜底角为α，双棱镜可看作是两个直角三棱镜，由于光的色散作用，平行光垂直通过直角三棱镜第一个面入射面折射，再通过第二个面出射面折射时，i1为出射面折射时的入射角，β为偏向角，由图中几何关系知，α=i1，入射角i1=α，折射角i2=α+β，则根据折射定律，双棱镜折射率n为：

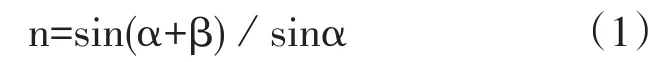
从理论上来讲，通过望远镜直接观察棱镜光谱，对准某一条谱线（如绿线）使竖直叉丝和谱线完全重合，记录刻度盘上两游标读数，通过分光仪测出α和β，即可测出双棱镜的折射率。但在实验时，仅用双棱镜一次分光，用望远镜直接观察谱线时发现，由于双棱镜的底角α比较小，直角三棱镜出射光进入到望远镜的光能量有限，导致观察到的光谱线比较宽且强度非常弱，不便于观察及测量偏向角β，且只有一级光谱。若先通过双棱镜一次分光后，然后通过光栅进行二次分光，再通过望远镜观察，由于二次分光时发生的是光栅衍射，既要考虑多缝夫琅禾费衍射，也要考虑多光束干涉，由于多光束干涉的结果，导致光谱线非常明亮非常细锐，方便观察及测量，并且得到多级的彩色光谱线，大大提高了测量精度。

在光栅进行二次分光时，由图1知，光的入射方式为斜入射，光栅在斜入射条件下的光栅方程为[4-8]

（2）式中，θ为衍射角，θ0为斜入射时的入射角，当入射线和衍射线在法线同侧时为正，异侧时为负，当θ=θ0时，对应的谱线为零级谱线，即k=0，因此，只要通过分光仪测出零级谱线对应的衍射角θ，即可测出斜入射时的入射角θ0，依据光路可知偏向角β就等于θ0，因此，只要测出零级谱线对应的衍射角θ，即可测出β。

由以上分析可知，通过光栅的二次分光，可得到非常明亮非常细锐的光谱线，可以方便测出偏向角β，若再用自准直法测出双棱镜的底角α，将α和β代入公式（1），即可测出双棱镜的折射率n。

2.2 测量双棱镜折射率的简要实验方法

（1）双棱镜底角α的测量

图2所示为利用自准直法测双棱镜底角α的简单示意图。测量时将双棱镜置于分光计载物台上，打开望远镜小灯，转动望远镜，使望远镜对准双棱镜的一个折射面，用自准直法调节望远镜的光轴与此折射面严格垂直，即使绿十字反射像和调整叉丝完全重合，记录刻度盘上两游标读数ν1和ν1′，再转动望远镜，用同样方法使望远镜光轴垂直于双棱镜第二个折射面，记录相应的游标读数ν2和ν2′，同一游标前后两次读数之差等于棱镜角A的补角，即

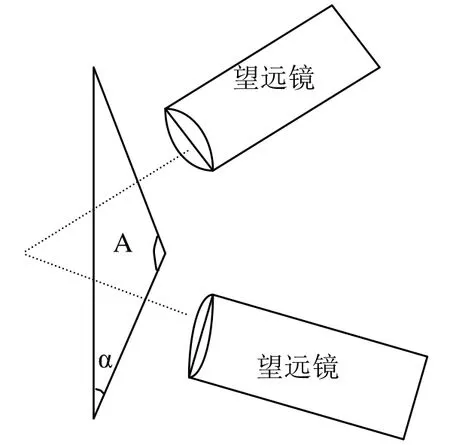
图2 双棱镜底角测量示意图

（2）β角的测量

关掉望远镜小灯，让准直管出射的平行光先通过双棱镜分光，再通过光栅分光，如图1所示，通过望远镜可观察到彩色光谱线，转动望远镜，对准某一条谱线（如绿线）使竖直叉丝和谱线完全重合，记录刻度盘上两游标读数u1和u1′，再转动望远镜，用同样方法用望远镜对准另一侧谱线，记录刻度盘上相应的游标读数u2和u2′，同一游标前后两次读数之差等于2β，即

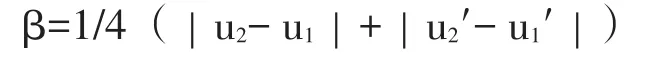
3 光波波长及光栅常数的测量

当光栅进行二次分光时，由于双棱镜相当于两个三棱镜，每一个三棱镜对应的平行出射光都斜入射于光栅平面，但根据对称性，一组向上偏，一组向下偏，相当于一个三棱镜通过光栅的二次分光可以得到一组彩色光谱线。由于是斜入射，两侧不对称，两个三棱镜均分光得到两组彩色光谱线，非相干地叠加在一起，即可得到两侧对称的彩色光谱线，谱线的数目是一个三棱镜的谱线数目的两倍。其光栅方程仍为

dsin(θ±θ0)=kλ

若已知绿光波长λ，先确定级数k，再利用分光仪测出零级谱线衍射角θ0及第k级谱线衍射角θ，即可测出光栅常数，根据测得的光栅常数，确定级数k，再利用分光仪测出零级谱线衍射角θ0及第k级谱线衍射角θ，即可测出未知光波波长。

4 结语

综上所述，在大学物理光学实验教学中，棱镜和光栅是最基本的分光元件，但二者的分光机理不同。棱镜光谱属于几何光学的范畴，而光栅光谱属于波动光学的范畴。在分光仪上若将复色光先通过棱镜分光再通过光栅进行二次分光，可以将棱镜得到的一级彩色光谱转化成多级彩色光谱。利用光栅进行二次分光时，由于既考虑了单缝衍射也考虑了缝间干涉，得到的光谱线非常细锐非常明亮，既方便观察光谱线也便于精确测量衍射角及折射角，进而可以非常方便地测出双棱镜的折射率、光波波长及光栅常数。几何光学是波动光学的一种极限、一种近似，分光实验中将棱镜和光栅两种分光机理不同的分光元件结合起来进行分光，便于学生更进一步理解几何光学和波动光学是一个统一的整体。棱镜光栅组合分光在大学物理光学理论及实验教学中都具有重要意义，同时也是对几何光学和波动光学理论及实验教学的拓展和完善。