极限平衡条件在土体剪切平衡状态中的应用

李晓莲，杨 静，魏秦生，吕向明

（1.天水师范学院 土木工程学院，甘肃 天水 741001；2.天水师范学院 机电与汽车工程学院，甘肃 天水 741001；3.中石油第二建设公司，甘肃 兰州 730060）

当土体受力后处于三向应力状态时，如果土体中任意一点在其某一方位上的剪应力τ等于该方位的抗剪强度τf，则该点就处于极限平衡状态，[1]也就是说此时土体处于将要破坏而又没有破坏的界限状态；而当土体中任意一点在其某一方位上的剪应力大于该方位的抗剪强度时，该点即破坏。根据上述条件，即可判断土体中某点所处状态。如果将土体中某点的应力状态用莫尔应力圆来表示，并同时将其与土体的抗剪强度包线即库伦强度包线，绘制在同一σ-τ坐标图上，即可根据莫尔应力圆与库伦强度包线之间的相对位置关系判断土体所处状态。其中当莫尔应力圆与库伦强度包线相切时，即该点（某一方向上）的剪应力等于抗剪强度，就是土体的强度条件，[2]土体的状态称为极限平衡状态。此时土的大、小主应力与土的抗剪强度指标之间的关系称为土的极限平衡条件。[3]由于该条件是由莫尔应力圆与库伦强度包线相切的几何关系所建立，所以该条件也称为莫尔-库伦强度理论，根据土的极限平衡条件就可以判断土体中任意一点的剪切破坏状态。

下面以平面应变问题为例，通过分析莫尔应力圆与库伦强度包线之间的关系，建立土体的极限平衡条件，给出土体任意一点的剪切破坏状态判断的七种方法。

1 莫尔应力圆与抗剪强度之间的关系

如果已知某土体的抗剪强度指标c、φ及剪切破坏面上的法向总应力σ（c为土体的粘聚力，φ为土体的内摩擦角），可以将库伦公式τf=c+σtanφ在σ-τ坐标图上表示为一条直线-抗剪强度包络线，即库伦强度包线；如果已知土体某点的应力状态（平面应力状态），利用应力圆原理，可以将该点各个方位上的应力情况在σ-τ坐标图上表示为莫尔应力圆，简称莫尔圆。将上述抗剪强度包线与莫尔圆绘制在同一张坐标图上（如图1所示），它们之间的关系就可能有以下三种情况：

1.1 相离

此时，整个莫尔圆（圆1）位于抗剪强度包线的下方，说明该点所有方位上的剪应力都小于对应平面上的抗剪强度，即τ＜τf，因此该点处于安全状态。

图1 莫尔应力圆与抗剪强度之间的关系

1.2 相切

此时，莫尔圆（圆2）与抗剪强度包线相切于一点，切点为A，说明在A点所对应的平面上，其剪应力刚好等于抗剪强度，即τ=τf，因此该点处于极限平衡状态，A点所对应的平面即为试样的剪切破坏面，此时应力圆2称为极限应力圆。

图2 土体中某点处于极限平衡状态时的应力圆

1.3 相割

此时，莫尔圆（圆3）与抗剪强度包线相交，即抗剪强度包线是应力圆的一条割线，理论上说明该点一部分方位上的剪应力大于对应平面上的抗剪强度，即τ＞τf。但实际上这种情况不可能出现，因为该点任何方向上的剪应力在与其对应平面上的抗剪强度相等时就已经破坏，不可能再出现超过土的抗剪强度的现象，即不存在τ＞τf，因为当土体剪应力达到其抗剪强度时，应力已不符合弹性理论解答。[4]

2 极限平衡条件的建立

土体极限平衡条件就是根据莫尔圆与抗剪强度包线相切的几何关系建立的。

在平面问题中，土的极限平衡条件是由莫尔—库伦强度理论所确定：当莫尔圆与抗剪强度包线相切时，土体即处于极限平衡状态，由极限应力圆与抗剪强度包线相切的几何关系（如图2所示），针对粘性土（c≠0）建立的极限平衡条件为：

针对非粘性土(c=0)建立的极限平衡条件为：

式（1）-（4）中，σ1、σ3为实际应力状态对应的第一主应力与第三主应力，σ1f、σ3f为土体处于极限平衡状态时某点应有的第一主应力与第三主应力值，φ为土体的内摩擦角。

3 土体剪切破坏状态的判断方法

土体所处状态的判断通常采用极限平衡条件，除此之外，还可以根据极限平衡状态时土体内摩擦角与实际工作状态下土体的内摩擦角之间的大小关系去判断，或者利用极限应力圆半径与实际应力圆半径之间的大小关系进行判断等等。下面简单介绍判断土体所处状态的几种方法。

3.1 极限平衡条件法

利用极限平衡条件法判断土体所处状态，是根据建立的极限平衡条件，通过计算，将实际情况下的大小主应力与该土体处于极限平衡条件下的大小主应力做比较，从而判断土体是否已被剪坏。

利用极限平衡条件中的表达式，知道土中某点实际所受的应力和土的抗剪强度指标c、φ，就可以很容易判断该点是否产生剪切破坏。比较计算所得极限平衡条件下的主应力与实际工作状态下的主应力数值大小，判断土体某点所处状态情况如下：

（1）σ1f＜σ1：土体中某点处于破坏状态（不可能状态）；

（2）σ1f=σ1：土体中某点处于极限平衡状态（破坏）；

（3）σ1f＞σ1：土体中某点处于弹性平衡状态（安全）。

或

（1）σ3f＞σ3：土体中某点处于破坏状态（不可能状态）；

（2）σ3f=σ3：土体中某点处于极限平衡状态（破坏）；

（3）σ3f＜σ3：土体中某点处于弹性平衡状态（安全）。

由以上条件可知：当σ1f=σ1或σ3f=σ3时，莫尔应力圆与抗剪强度包线相切，在切点所对应的方位上，土体的剪应力等于其抗剪强度，土体处于极限平衡状态，即将要破坏而又没有破坏的状态，实际上此时土体应划为破坏状态；当σ1f＞σ1或σ3f＜σ3时，莫尔应力圆与抗剪强度包线相离，应力圆位于抗剪强度包线的下方，说明该点所有方位上的剪应力均小于其抗剪强度，土体处于弹性平衡状态，或称稳定状态，即此时土体安全；当σ1f＜σ1或σ3f＞σ3时，莫尔应力圆与抗剪强度包线相交，应力圆与抗剪强度包线有两个交点，说明这两点及之间所对应的方位上的剪应力均大于其抗剪强度，土体处于破坏状态。实际上σ1f＜σ1或σ3f＞σ3是不可能存在的，因为严格来讲，当σ1f=σ1或σ3f=σ3时土体即开始破坏，不存在σ1f＜σ1或σ3f＞σ3的情况。

由应力圆的应用特点可知，在图2中，αf为剪切破坏面的方位角，在三角形ARD中，由外角与内角的关系可知：

式（5）表明，剪切破坏面与大主应力σ1作用面的夹角为，或剪切破坏面与小主应力σ3作用面的夹角为。由于土体与其他连续性材料不同，是一种具有内摩擦强度的材料。[5]所以，土体的剪切破坏并不产生于最大剪应力所在平面，而是在与最大剪应力面成φ/2夹角的面上，且通过土中一点可以出现一对滑动面，[3]这对滑动面均与大主应力的作用面成αf的夹角，如图2所示。

3.2 图解法

将实际工作状态下的莫尔应力圆和土体的抗剪强度包线绘制在同一坐标系中，[6]利用抗剪强度包线和应力圆的位置关系判断土体所处状态的结果如下：

（1）相离：土体中某点处于破坏状态（不可能状态）；

（2）相切：土体中某点处于极限平衡状态（破坏）；

（3）相割：土体中某点处于弹性平衡状态（安全）；

判断结果如图1所示。

3.3 内摩擦角法

若已知土中某点的主应力σ1、σ3，以及土体的内摩擦角φ，也可以用内摩擦角φ的大小判断该点土体是否处于破坏状态。

由图2极限平衡状态时的应力圆与抗剪强度包线之间的关系可知：

上式中，φ为实际工作状态下的内摩擦角，φm为土体达极限平衡状态时的内摩擦角。

根据计算所得φm与φ的大小关系，即可判断土体某点所处状态情况如下：

（1）φ＞φm：土体中某点处于破坏状态（不可能状态）；

（2）φ=φm：土体中某点处于极限平衡状态（破坏）；

（3）φ＜φm：土体中某点处于弹性平衡状态（安全）。

如果φ＞φm，表示保持土中某点不发生破坏所需的内摩擦角大于土的极限平衡状态时的内摩擦角。显然，此时土体已破坏。若φ＜φm，则土中某点处于安全状态，即弹性平衡状态。当φm=φ，则表示土中某点刚好处于极限平衡状态，即将要破坏而又没有破坏状态，或称塑性平衡状态。结果如图3所示。

图3 实际工作状态下的内摩擦角与极限平衡状态时内摩擦角的关系

3.4 斜率法

将土的抗剪强度包线与实际工作状态下的应力圆绘制在同一坐标，如图4所示。过点A（0，c）作莫尔应力圆的切线,设切线的斜率为K=tanφ,设抗剪强度包线的斜率为Km=tanφm，则有：

（1）Km＜K：土体中某点处于破坏状态（不可能状态）；

（2）Km=K：土体中某点处于极限平衡状态（破坏）；

（3）Km＞K：土体中某点处于弹性平衡状态（安全）。

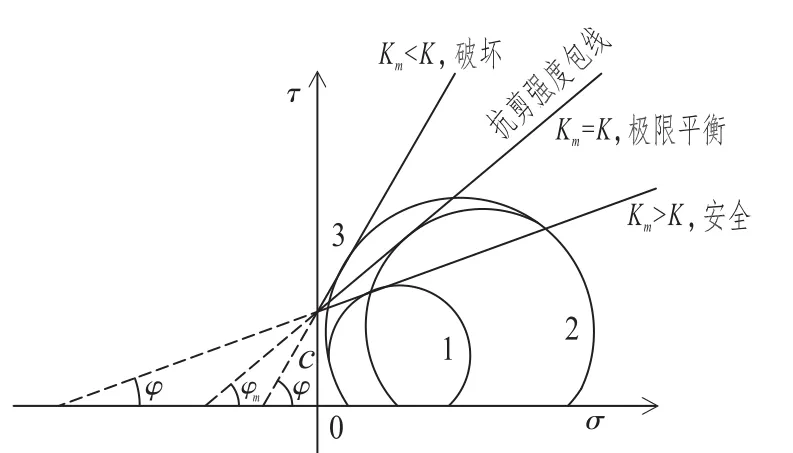
图4 莫尔应力圆切线斜率与抗剪强度包线斜率之间的关系

3.5 薄弱面法[7]

如前所述，土体达极限平衡状态时的剪切破坏面(即最薄弱面)与大主应力σ1作用面的夹角为，利用求出最薄弱面上的剪应力τ和法向应力σ,然后把法向应力σ代入抗剪强度的计算公式τf=c+σtanφ中，求出最薄弱面上的抗剪强度τf。则根据最薄弱面上剪应力τ与抗剪强度τf的关系判断土体所处状态如下：

（1）τf＜τ：土体中某点处于破坏状态（不可能状态）；

（2）τf=τ：土体中某点处于极限平衡状态（破坏）；

（3）τf＞τ：土体中某点处于弹性平衡状态（安全）。

3.6 距离法

将土的抗剪强度包线与实际工作状态下的应力圆绘制在同一坐标。设d为应力圆圆心到抗剪强度包线的垂直距离，为应力圆半径。则根据d与r的关系判断土体所处状态如下：

（1）d＜r：土体中某点处于破坏状态（不可能状态）；

（2）d=r：土体中某点处于极限平衡状态（破坏）；

（3）d＞r：土体中某点处于弹性平衡状态（安全）。

3.7 半径法

极限平衡条件的应用除了上述几种方法之外，还可以用图解法判断土中某点的安全状态，也可称之为半径法。

设想由于某种原因可以使得整个土体在水平方向均匀的伸展或压缩，[1]即可以任意增加或减小土中应力值。将极限平衡状态时的应力圆半径用Rf来表示，实际工作状态下的应力圆半径用R来表示。

（1） 当σ3→σ1f时，比较若得σ1f＞σ1，则有半径，[8]即实际工作状态下土体中某点的应力圆半径小于极限平衡状态时土体中某点的应力圆半径，此时实际应力圆位于极限应力圆下方，说明此时该点所有方位上的剪应力均小于其抗剪强度值，故土体中该点未达到极限平衡状态，处于安全状态；反之，则发生了剪切破坏。将此时的实际应力状态所对应的应力圆与极限应力圆之间的半径关系表示于σ-τ坐标图中，如图5中圆I与圆II所示。

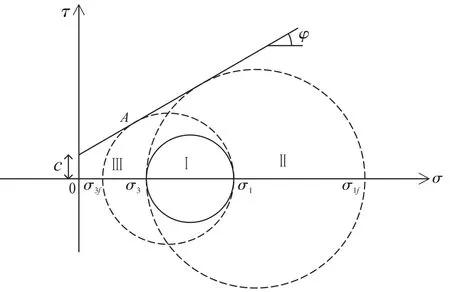
图5 实际应力圆半径与极限应力圆半径之间的关系

（2） 当σ1→σ3f时，比较若得σ3f＜σ3，则有半径，即实际工作状态下土体中某点的应力圆半径小于极限平衡状态时土体中某点的应力圆半径，此时实际应力圆位于极限应力圆下方，说明此时该点所有方位上的剪应力均小于其抗剪强度值，故土体中该点未达到极限平衡状态，处于安全状态；反之，则发生了剪切破坏。[9]将此时的实际应力状态所对应的应力圆与极限应力圆之间的关系表示于σ-τ坐标图中，如上图5中圆I与圆III所示。

上述情况也可表述为：当σ1f＜σ1，即极限应力圆半径小于实际应力圆半径，此时实际应力圆与抗剪强度包线相交，所以该点处于剪破状态，反之，该点处于安全状态；或当σ3＜σ3f时，极限应力圆的半径小于实际应力圆半径，即实际应力圆与抗剪强度包线相交，所以该点处于剪破状态，反之，该点处于安全状态。由实际应力圆半径与极限应力圆半径之间的大小关系判断土体剪切状态的方法，即称之为半径法。

用半径法判断土体的剪切状态直观、可靠、简便。

4 实例分析

设地基中某点的大主应力为450kPa，小主应力为100kPa，土的内摩擦角为30°，粘聚力为10kPa，问该点处于什么状态？

解法一：已知σ1=450kPa，σ3=100kPa，

由极限平衡条件，可得

则有σ3f＞σ3，由极限平衡条件法可以判断此时土中该点已破坏。或者，由极限平衡条件，可得：

则有σ1f＜σ1，由极限平衡条件法可以判断此时土中该点已破坏。

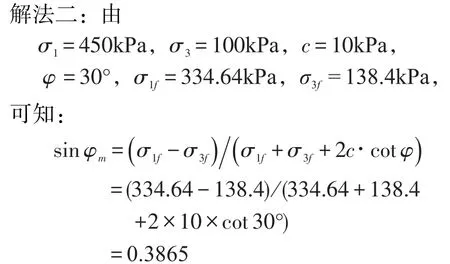
即φm=22.74°，而在实际工作状态下，φ=30°，比较可知，φ＞φm，由内摩擦角法可以判断此时土中该点已破坏。

解法三：由解法一和解法二可知，极限平衡状态时的大、小主应力分别为σ1f=334.64kPa，σ3f=138.4kPa，而实际工作状态下该点的大、小主应力分别为σ1=450kPa，σ3=100kPa，则有：

显然，R＞Rf，根据半径法可以判断此时土中该点已破坏。

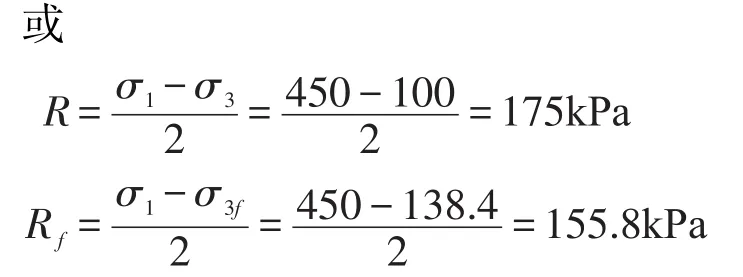
显然，R＞Rf，根据半径法可以判断此时土中该点已破坏。

由上述实例结果可知，三种判断方法结果一致。

5 小结

当抗剪强度包线与莫尔应力圆的图形位置相切时，土体即处于极限平衡状态，由此得出土的极限平衡条件。根据土的极限平衡条件判断土体所处状态的方法有多种，文中总结了七种，并用实例说明其结果的一致性。几种方法虽然形式不同，但基本原理一致，都是根据土体处于极限平衡状态时莫尔应力圆与抗剪强度包线相切的原理推得的，对于土体所处状态的判断具有很好的借鉴意义。