城市轨道交通大小交路结合 快慢车开行方案优化

段凌林 ，查伟雄，李 剑，严利鑫

（1.华东交通大学 交通运输与物流学院，江西 南昌 330013；2.华东交通大学 交通运输与经济 研究所，江西 南昌 330013)

0 引言

对于不同区段断面客流差异较大的城市轨道交通线路，为了适应客流需求，在高峰期实行大小交路与快慢车组合的运营模式，可以在提升长距离乘客旅行速度的同时提高繁忙区段的发车密度，提升运营效率。为此，在大小交路结合快慢车的列车开行模式下，制订科学合理的列车开行方案对城市轨道交通列车运行组织非常重要。

国内外学者对城市轨道交通列车开行方案问题进行了大量的研究。牛惠民等[1]考虑乘客等待时间作为目标函数的影响因素；邓连波等[2]同时考虑企业运营成本和乘客出行成本，将这2 个因素纳入目标函数中进行优化。城市轨道交通线路的区段客流不均衡，容易导致客流密度较低区段的运力浪费，为解决这一问题，王媛媛等[3]与许得杰等[4]引入大小交路的运营模式，根据折返站的位置，将客流分类并分别计算乘客的出行成本；Tirachini 等[5]采用“广义成本平方根”的方法推导各交路列车的开行频率。采用大小交路模式虽然提高了小交路区段的运输能力，但是却使长距离乘客的旅行时间增加，乘客的出行成本上升。为减少长距离乘客的旅行时间，汤莲花等[6]在多交路的基础上引入快慢车运营模式，优化乘客出行时间与企业运营成本。孙元广等[7]在研究快慢车开行方案优化问题时，优化列车周转时间，但没有考虑停站时间的优化问题。

目前，城市轨道交通列车开行方案的研究一般只考虑独立采用大小交路或快慢车的模式，鲜有将大小交路与快慢车2 种模式组合，也没有优化列车在各站的停站时间。为此，考虑客流需求，在大小交路模式的基础上引入快慢车模式，以乘客出行成本与企业运营成本最小为目标，构建双目标整数规划模型，优化大小交路与快慢车模式下，大交路快车、大交路慢车和小交路慢车的发车频率，以降低乘客出行成本和企业运营成本。

1 城市轨道交通大小交路结合快慢车开行方案优化模型

1.1 基本假设

设1 条城市轨道交通线路共有N 个车站，分别 为s1，s2，…，sε1，sε2，…，sN，其 中 车 站s1与sN为线路起终点站，车站sε1与sε2为折返站。γ 为列车运行方向，s1至sN方向为上行方向，γ = 1；反之为下行方向，γ = 2。线路起终点站间(s1—sN)开行全线贯通的大交路快车和慢车，在折返站区段(sε1—sε2)开行小交路慢车。表示列车交路种类n在车站s 是否停站，取值的含义为fn为第n 种交路列车的发车频率；si为乘客出行的起点站，sj为乘客出行的终点站；为自si至sj的乘客选择乘坐列车交路种类n 的客流比例，其取值与，fn有关。大小交路与快慢车结合开行方案如图1 所示。

考虑城市轨道交通列车开行实际情况，作出以下假设：①乘客选择直达列车到达目的地，中途不换乘；②乘客均匀到达出发车站，并乘坐第1 列可以乘坐的列车，不存在乘客滞留的情况。

1.2 目标函数

城市轨道交通列车开行方案优化模型涉及供给方(运营企业)与需求方(乘客)2 个主体，其成本是一对博弈制衡的关系。乘客出行成本最小目标要求尽可能多地开行列车，以减少乘客的等待时间，而这会导致企业运营成本的增加。因此，模型应以乘客出行成本与企业运营成本最小为目标，寻求开行频率的均衡点。

1.2.1 乘客出行成本。

乘客出行成本以乘客的出行时间衡量。乘客的出行时间包括站台候车时间与在途时间。由于实行大小交路与快慢车结合的运营方式，客流选择的列车交路不同，或途经的线路区间不同，其出行时间不同。因此，根据折返站的位置，将线路划分为3 个区段，其中车站s1至sε1为区段Ⅰ，车站sε1至sε2为区段Ⅱ，车站sε2至sN为区段Ⅲ。列车交路区段划分如图2 所示。

n 为列车交路种类，取值的含义为

图1 大小交路与快慢车结合开行方案Fig.1 Operation mode combining full-length and short-turn routing with express and slow train

图2 列车交路区段划分Fig.2 Division of train routing section

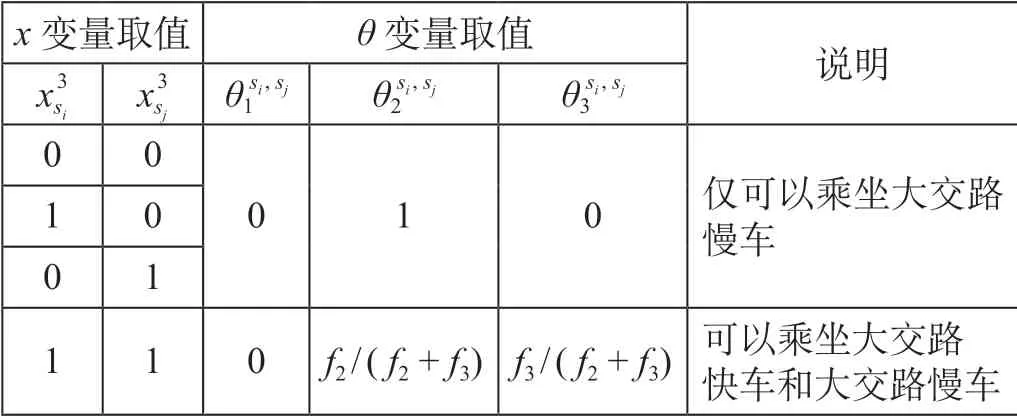
表1 区段Ⅰ或区段Ⅲ上车乘客列车分担客流比例Tab.1 Sharing rate of passenger boarding at segment I or segment III

对于在区段Ⅱ上车的乘客，讨论由车站sε1至车站sε2-1(ε1≤i ≤ε2- 1)上车乘客的候车时间。该区段开行3 种列车，由于小交路的存在，在上车站点分区段的基础上，对乘客下车站进行划分，将下车站划分为车站sε1+1至车站sε2(ε1+ 1 ≤j ≤ε2)与车站sε2+1至车站sN(ε2+ 1 ≤j ≤N)。区段Ⅱ上车乘客列车分担客流比例如表2 所示。

式中：cw1为上行方向乘客站台候车时间；cw2为下行方向的乘客站台候车时间；qsi,sj为在车站si上车且在车站sj下车的客流量。的取值方法参见表1和表2。

乘客站台候车的总时间计算公式为

式中：cw为乘客站台候车的总时间。

乘客的在途时间由列车纯运行时间与停站时间2 部分构成。对于相同起终点的乘客，由于列车纯运行时间相同，因而可以只考虑列车停站时间对乘客在途时间的影响。列车停站时间与高峰期该车站的上、下车人数，高峰小时开行列车对数，平均每人上、下车时间，列车编组数，每车每侧车门数，列车开关门时间以及车内乘客与站台乘客的不均匀系数有关。上行方向列车在车站sk的停站时间计算公式为

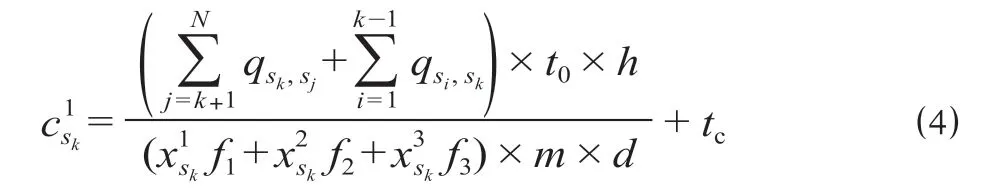
上行方向乘客所消耗的总停站时间为

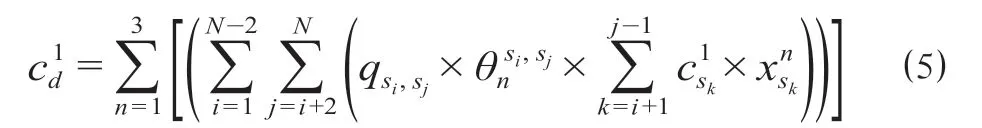
同理，下行方向列车在sk站的停站时间为

表2 区段Ⅱ上车乘客列车分担客流比例Tab.2 Sharing rate of passenger boarding at segment II

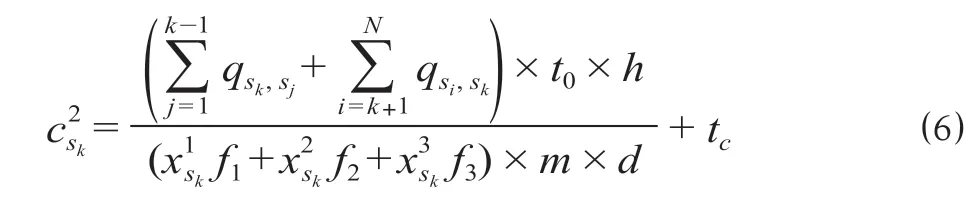
式中：cd为列车停站所消耗的乘客时间。

乘客总出行时间为

式中：cT为乘客总出行时间。

1.2.2 企业运营成本。

企业运营成本可以分为固定成本与可变成本。由于固定成本为定值，对结果影响较小，在模型中不考虑。可变成本与列车停站成本、列车运行成本有关。其中，列车停站成本与停站次数有关，列车运行成本与列车公里数有关。由于大小交路与快慢车的停站次数不同，导致不同运营方式的停站成本不同。列车停站成本计算公式为

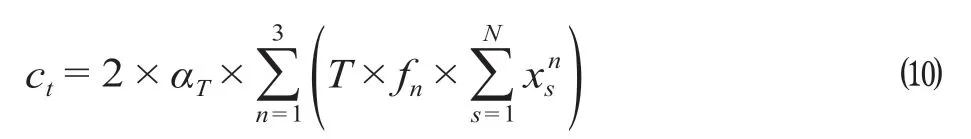
式中：ct为总列车停站成本；αT为单次停站成本。

列车的可变成本与列车走行公里有关，计算公式为

式中：cy为总列车运行成本；αB为单位车辆里程费用。

因此，企业运营成本可以表示为

式中：c0为企业运营成本。

1.3 约束条件

由于线路的承载能力有限，列车的发车频率有一定的限制。线路发车频率约束可以用以下公式 表示

式中：f0为线路最小发车频率；fM为线路最大发车频率。

列车开行应可以满足该时段的乘客需求，即途经某断面的列车的总定员应大于该断面客流。由于上、下行采用同样的开行方案，因而取上、下行方向中较大的断面客流作为约束。因而sk站与sk+1站之间上、下行方向断面客流的较大值计算公式为

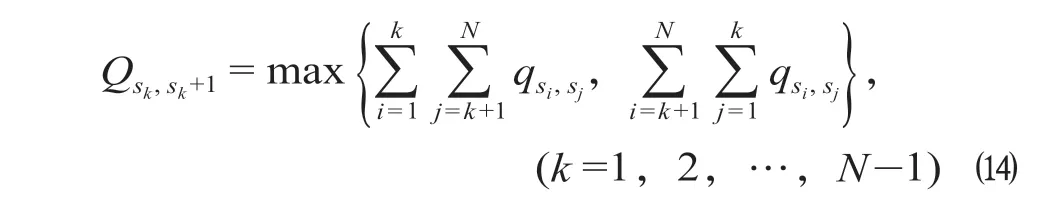
式中：Qsk,sk+1为sk站与sk+1站之间的上行方向与下行方向断面客流较大值。

由于区段Ⅰ与区段Ⅲ开行大交路快车和大交路慢车2 种列车，Ⅰ、Ⅲ区段开行列车总定员应大于该区段的上、下行各断面客流的较大值，对应的约束为

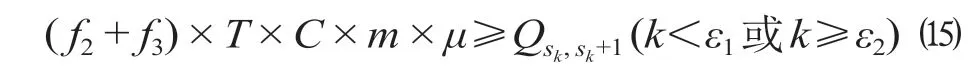
式中：C 为车辆定员；μ 为列车的满载率。

同理，由于区段Ⅱ开行小交路慢车、大交路快车、大交路慢车3 种列车，开行列车总定员应大于该区段的上、下行各断面客流的较大值，对应的约束为

1.4 求解算法

此优化模型为双目标非线性整数规划模型，需要将其转化为单目标整数规划问题求解。根据收入法，乘客的时间成本为人均小时工资的0.3 倍[8]。设pv为人均小时工资，此时2 个目标量纲相同，且乘客出行成本与企业运营成本需要同时优化至最小，因而将2 个目标进行加权相加，将双目标规划转化为单目标规划，得到以下转化后的目标函数为

转化后的模型为非线性整数规划模型，可以利用LINGO 12.0 进行求解。

2 算例分析

2.1 市郊线路分析

某城市轨道交通市郊线路共设24 个车站，编号1 至编号24，其中车站1 与车站24 为终点站，车站7 与车站17 为折返站。计划于车站7 至车站17 的区间开行小交路列车；于车站1 与车站24 的区间交替开行快车和慢车。大交路快车仅在车站1，7，8，13，17，24 停站。线路区间长度如表3 所示。

选取工作日早高峰(8 : 00—9 : 00)与晚高峰(5 : 30—6 : 30)的OD 客流数据作为输入条件。早高峰断面流量如图3 所示；晚高峰断面流量如图4所示。根据实际情况，模型参数取值如表4 所示。

表3 线路区间长度Tab.3 The length of the segment of the line

2.2 计算结果分析

求解单一交路与大小交路嵌套的运营模式，得到不同运营模式下的最优发车频率如表5 所示。

根据求解结果，高峰时期不同运营模式的列车运营指标如表6 所示；各种运营模式相比列车运营指标变化率如表7 所示。

图3 早高峰断面流量Fig.3 Passenger flow volume of stations on the morning peak

图4 晚高峰断面流量Fig.4 Passenger flow volume of stations on the evening peak

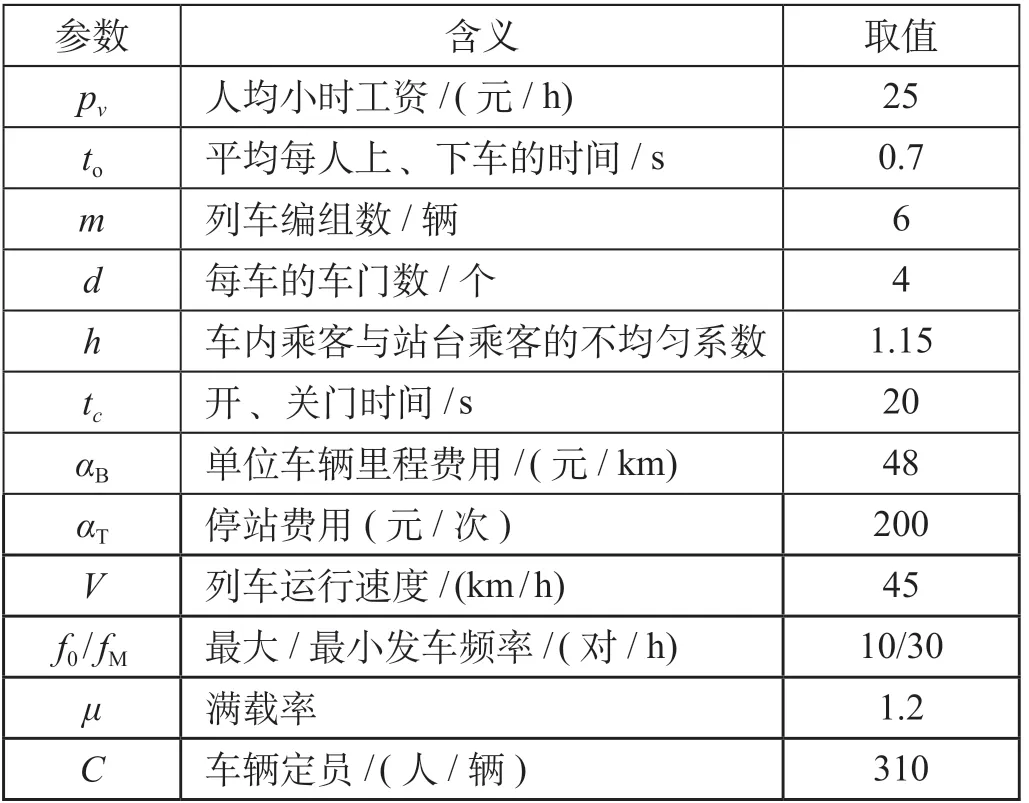
表4 参数取值Tab.4 Parameter value

由表7 可知，相比单一交路的运营模式，采用大小交路嵌套模式的早高峰企业运营成本降低19.29%，晚高峰企业运营成本降低20%，但是乘客在站台的等待时间有较大程度的延长，导致乘客出行成本的增加。而大小交路的基础上加入快慢车的运营模式，虽然也延长了乘客在站台的等待时间，但是乘客在途时间和总旅行时间均有所减少，早、晚高峰乘客出行成本均有所降低。综合考虑乘客出行成本和企业运营成本，采用大小交路结合快慢车模式后，早高峰总成本降低了6.77%，晚高峰总成本降低了5.21%。

表5 不同运营模式下最优发车频率Tab.5 Optimal frequency on different operation modes

表6 不同运营方式的列车运营指标Tab.6 Train operation index of different operation modes

表7 列车运营指标变化率 %Tab.7 Change rate of train operation index

3 研究结论

（1）考虑最大断面客流与线路能力等约束，建立双目标非线性整数规划模型，运用线性加权法将双目标模型转化为单目标模型。结果表明，该模型可以实现城市轨道交通大小交路结合快慢车开行方案的优化。

（2）城市轨道交通线路在大小交路的基础上加开快慢车，可以兼顾运营企业与乘客两者的利益，减少部分乘客的停站时间，缓解乘客的出行时间消耗，同时降低企业的停站成本。

（3）考虑快车是否停站的优化模型有待进一步研究。