金属有机骨架与相变芯材相互作用的分子动力学
海广通,薛祥东,苏天琪,魏永强,高志猛,马雨威,王静静✉
1) 北京科技大学材料科学与工程学院,北京 100083 2) 苏州阿德旺斯新材料有限公司,苏州 215000
随着化石能源的日益枯竭,如何提高能源的利用率成为当前科学界广泛研究的热点课题.储能技术正是在这样的背景下得以蓬勃发展的新能源技术,旨在有效解决当前能源利用中存在的时域与空域在供需关系上不匹配的问题[1].作为一种典型的储能技术,相变储能是实现热能高效存储与利用的有效途径,而实现相变储能的基础则是相变材料的开发与研究.基于固相-液相转变的相变材料由于其相变焓值较大,膨胀系数较小等诸多优点而备受关注[2].然而,这一类材料普遍存在相变材料在熔融状态的泄漏问题[3].因此,开发出一种可靠的载体材料实现相变芯材的有效封装,进而构筑兼具高热导率,高相变潜热及优异循环稳定性的定形复合相变材料具有重要的科学意义和应用价值.
金属有机骨架材料(metal-organic frameworks,MOFs)由于其具备规整的孔道结构、较高的孔隙率、超大的比表面积等结构优势而在催化[4]、气体存储[5]等领域被广泛应用.近年来科学家开始利用金属有机骨架材料作为载体开发新型定形复合相变材料.尤其是其孔道结构的可设计性,功能基团的可修饰性使其成为研究载体与相变芯材相互作用的理想材料.此外,十八酸、十八胺、十八醇和十八烷由于具备合适的相变温度(50~80 ℃),较大的相变潜热(120~300 J·g-1)而成为广泛应用的相变芯材[6],因此将其与金属有机骨架材料进行复合有望获得高性能的复合相变材料.但是两者的复合会引起相变芯材相变温度及结晶性等一系列理化性质的变化,这是由于相变芯材和金属有机骨架基体孔道内表面基团的相互作用引起的,因此研究两者之间的相互作用进而指导高性能复合相变材料的开发具有重要意义[7-10].
本文采用分子动力学的方法,选取热稳定性较高的金属有机骨架材料Cr-MIL-101与上述四种相变芯材以及由它们所构筑的复合体系进行了结构特性研究,包括芯材与金属有机骨架基体之间的相互作用以及芯材在金属有机骨架孔道内的分布特性,并比较了不同官能团对这些结构特性的影响,为该类复合相变材料的开发与设计提供了一定的理论依据和参考数据.
1 模型与算法
构筑的Cr-MIL-101的晶体结构模型如图1所示.图中可以看出,Cr-MIL-101具备规整的孔道结构,其孔径约为3 nm,可以有效填充十八酸等相变芯材,从而实现对相变芯材的有效封装.同时,Cr-MIL-101的单胞尺寸为6.284 nm×6.284 nm×6.284 nm,大于一般分子动力学模拟中截断半径的2倍,从而保证了计算模拟结果的可靠性.其填充相变芯材后的模型如图2所示,这里芯材的填充采用蒙特卡洛算法进行填充,模型中芯材质量负载率设置为70%[11],相变芯材的密度设置为0.9 g·cm-3,与真实的密度值基本吻合.
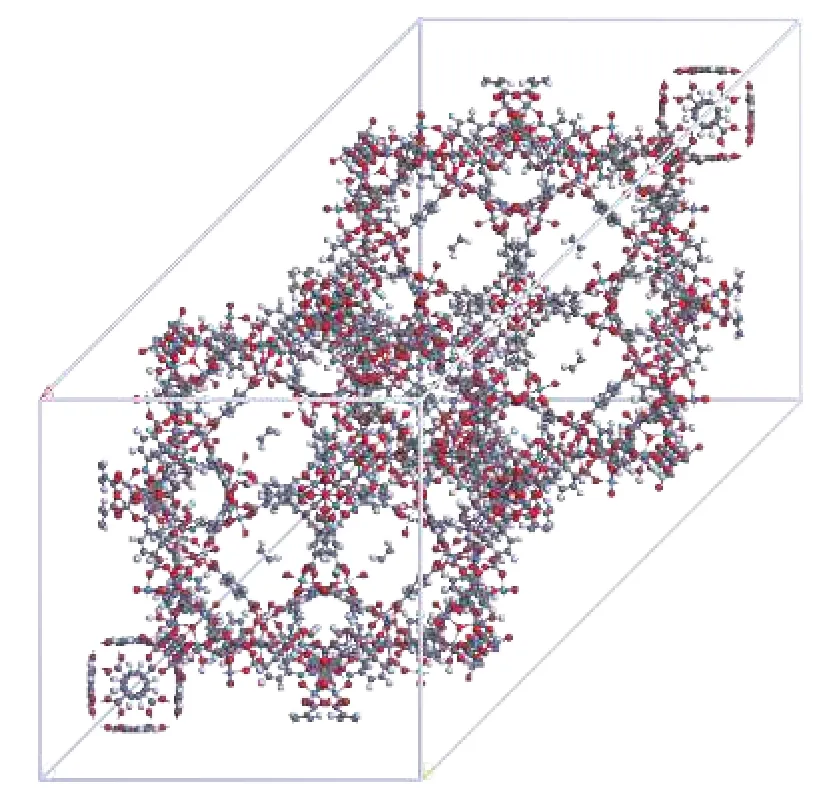
图1 Cr-MIL-101的晶体结构模型Fig.1 Crystal structure model of Cr-MIL-101
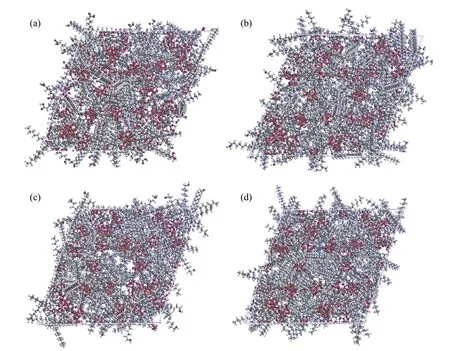
图2 Cr-MIL-101负载不同相变芯材的模型质量负载率为70%.(a) 十八酸;(b) 十八胺;(c) 十八醇;(d) 十八烷Fig.2 Structure model of Cr-MIL-101 loaded with different phase change core materials: (a) octadecanoic acid; (b) octadecylamine; (c) octadecanol; (d)octodecane
本文中的分子动力学模拟均在等温等压系宗下进行,温度为300 K,采用诺斯-胡佛链(NHL)恒温器施加热浴,其中Q比值的值为0.01,衰减常数为1 ps[12].采用Souza-Martins恒压器保证压力恒定,晶格时间常数设置为10 ps.为了保证模拟计算的稳定性,时间步长设为较小的1 fs,总的模拟时间为50 ps,并取最后10 ps的数据进行统计分析.分子间的作用势采用普适力场来描述,电荷分配方法则采用基于电负性平衡算法,考虑到与金属有机骨架体系的匹配性,收敛阈值选用5.0×10-4e.体系的静电势能通过埃瓦尔德(Ewald)求和算法来计算,范德华相互作用则采用基于原子的方法来描述,其截断半径设置为1.55 nm.
2 结果与讨论
2.1 Cr-MIL-101与相变芯材之间的相互作用能
相变芯材与金属有机骨架材料之间的相互作用能会显著影响芯材在金属有机骨架材料孔道中的分布与结晶度、相变焓等重要热学参数[13].因此研究不同相变芯材与金属有机骨架基体之间的相互作用能是很有意义的.通常,相互作用能的定义如下:

复合体系指两种物质复合之后的整体,基体指用作负载相变材料的载体物质,芯材指相变芯材,它们之间的相互作用能由分子动力学运动轨迹的最后10 ps的轨迹中每一帧的相互作用能的统计平均值给出,其中基体的能量为复合体系中移去芯材之后体系的能量值,芯材的能量为复合体系中移去基体之后的能量值.具体到本文中,基体为Cr-MIL-101,芯材分别为十八酸、十八胺、十八醇和十八烷.经过计算得到基体与芯材之间的相互作用能如表1所示.

表1 Cr-MIL-101与不同相变芯材之间的相互作用能Table 1 Interaction energy between Cr-MIL-101 and different phase change core materials
通过表格可以看出,十八酸芯材与金属有机骨架基体之间的相互作用最强,其次是十八醇和十八胺,十八烷最弱,这可能与十八烷的甲基基团有关.在十八酸、十八胺和十八醇分子中,电负性较强的氧原子和氮原子会带有局部负电荷,会与金属有机骨架基体中带有局部正电荷的原子(如金属原子等)之间产生静电相互作用(见表2),从而降低整个复合体系的能量.

表2 Cr-MIL-101与不同相变芯材之间的静电作用能Table 2 Electrostatic energy between Cr-MIL-101 and different phase change core materials
2.2 芯材分子的回转半径
回转半径是表征聚合物或者大分子在空间延展程度的物理量.由于聚合物分子通常具有大量的空间排列取向和不同的构型,所以通常用某些特性的统计(总体)平均值来描述分子链的构型.用于量化整体构型的其中一个重要参数就是回转半径.旋转半径s通常定义为分子中原子与其质心的均方根距离,即
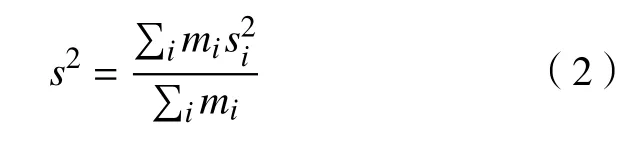
式中,si是第i个原子到质心的距离,mi为该原子的质量.
回转半径的分子动力学模拟结果如图3所示.在本文中,所有的回转半径都是基于相变芯材进行的.从图中可以看出,十八酸分子在金属有机骨架基体的孔道中回转半径较大,结合上述相互作用能的计算结果,推测这应当是十八酸分子和金属有机骨架基体之间的相互作用能较强,且表现为相互吸引作用,因此十八酸分子在孔道中受到周围金属有机骨架基体原子的吸引作用而被拉伸,从而增大了回转半径.同样的趋势可以在十八胺和十八醇分子的回转半径的计算结果中看到,十八醇分子的回转半径整体上大于十八胺分子的回转半径,这与十八醇分子与金属有机骨架基体之间的相互作用能更强的计算结果相一致.而十八烷分子与金属有机骨架基体之间的相互作用能较低,因此在孔道中表现出自发降低表面能的倾向,从而降低回转半径.回转半径的计算模拟结果与相互作用能的计算结果一致,表明这四种芯材在金属有机骨架孔道中存在不同的结构特性.
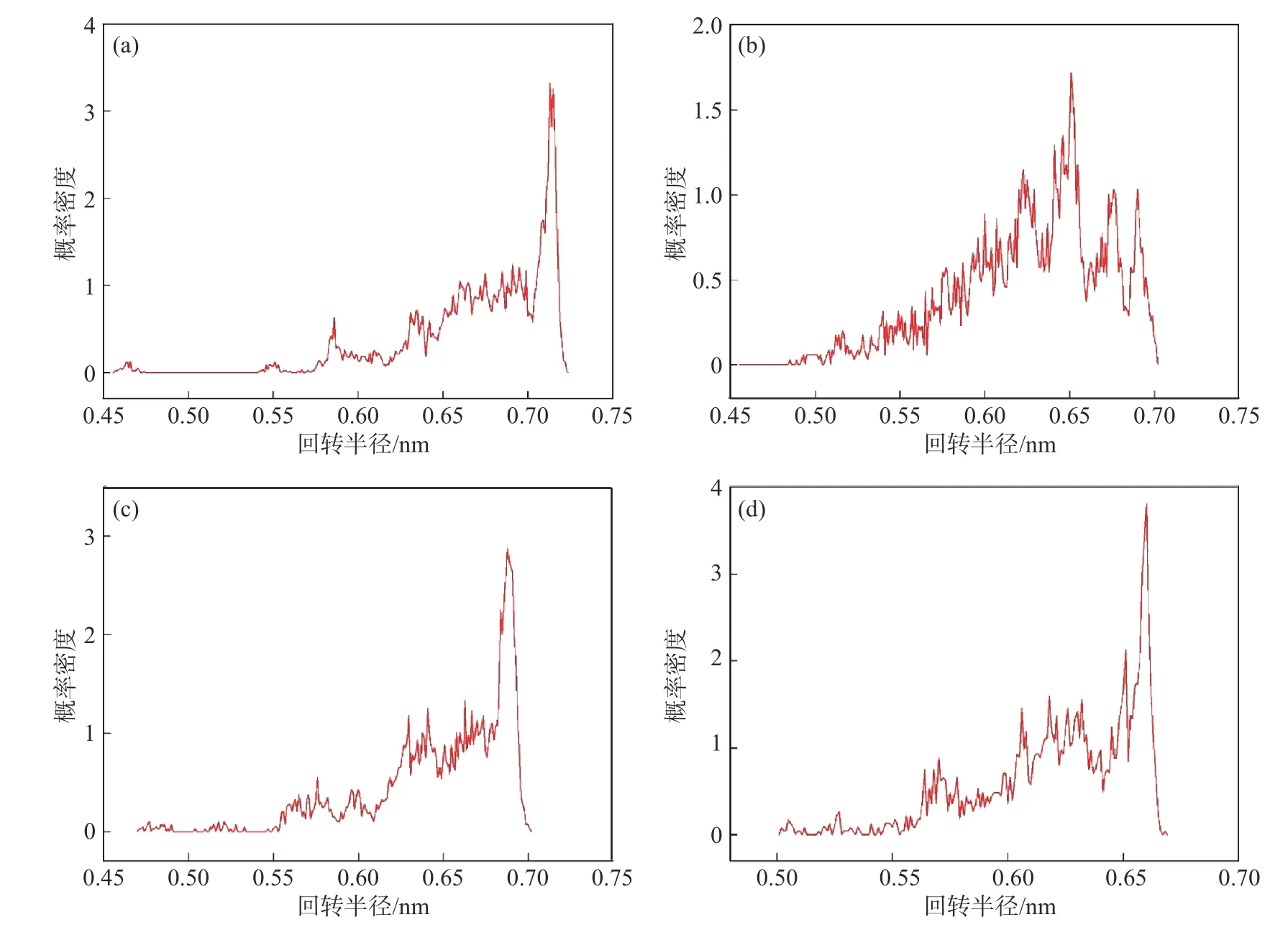
图3 不同复合相变材料回转半径的概率分布.(a) Cr-MIL-101@十八酸;(b) Cr-MIL-101@十八胺;(c) Cr-MIL-101@十八醇;(d) Cr-MIL-101@十八烷Fig.3 Probability distribution of radius of rotation: (a) Cr-MIL-101@octadecanoic acid; (b) Cr-MIL-101@octadecylamine; (c) Cr-MIL-101@octadecanol; (d) Cr-MIL-101@octodecane
2.3 芯材分子的扩散性质
均方位移分析是一种确定粒子随时间推移的位移模式的方法.特别是,可以帮助确定粒子是处于自由扩散、运输还是束缚状态.此外,均方位移分析还可以得到运动参数的估计,如自扩散系数.在分子动力学模拟中,可以直接从粒子的位置得到均方位移.如r(t)是时间t时粒子的位置,r(t+Δt)是经过时间间隔Δt之后粒子的位置,则粒子的平方位移为(r(t+Δt)-r(t))2.对平方位移取时间平均就得到了均方位移.均方位移作为时间间隔Δt的函数,通常在很短的时间间隔内以二次函数的形式增加(弹道区).如果粒子受到束缚,均方位移就会趋于稳定,是一个常数;如果粒子处于扩散状态,均方位移在时间上呈线性关系(扩散区),其斜率决定了(自)扩散系数D.根据爱因斯坦方程定义:

式中,MSD为均方根位移,Δt为时间.均方位移的模拟计算结果如图4所示.可以看出,在经历了一定长的时间后,粒子的均方位移随时间均表现出线性关系,说明粒子在孔道内处于扩散.根据爱因斯坦公式推导出的自扩散系数如表3所示.

图4 均方位移随时间的演化曲线.(a) Cr-MIL-101@十八酸;(b) Cr-MIL-101@十八胺;(c) Cr-MIL-101@十八醇;(d) Cr-MIL-101@十八烷Fig.4 Evolution curve of mean-square displacement with different times: (a) Cr-MIL-101@octadecanoic acid; (b) Cr-MIL-101@octadecylamine; (c) Cr-MIL-101@octadecanol; (d) Cr-MIL-101@octodecane

表3 不同相变芯材在金属有机骨架材料孔道中的自扩散系数Table 3 Self-diffusion coefficients of different phase change core materials in MOFs channel
从表格中可以看出,十八胺的扩散系数最高,这可能与十八胺分子与金属有机骨架基体之间存在适中的相互作用能有关,十八胺分子与金属有机骨架材料之间的相互作用与十八胺分子之间的相互作用相互抵消,使得十八胺分子处于较为自由的状态,从而使其具备较高的自扩散系数.对于十八酸和十八醇,其和金属有机骨架基体之间存在较强的相互作用,因而使得他们的扩散受到了一定的限制,因而出现扩散系数下降的现象.而十八烷分子与金属有机骨架基体之间相互作用较弱,在一定程度上会出现“表面能自发降低”带来的团聚现象,从而不利于扩散的进行,因而也使得扩散系数较低[14].以上结果表明当芯材分子与金属有机骨架基体之间有适中的相互作用能时,会使得芯材在孔道中处于较为自由的状态,从而有利于芯材的扩散;而芯材分子间的相互作用会使得芯材自发团聚,不利于扩散,并与芯材与金属有机骨架之间的相互作用产生相互抵消.当两者平衡时,就会增加扩散系数.当芯材分子与金属有机骨架之间的相互作用过强时,芯材会被金属有机骨架所束缚,从而也不利于扩散的进行.
2.4 芯材在金属有机骨架孔道内运动动能的分子动力学模拟
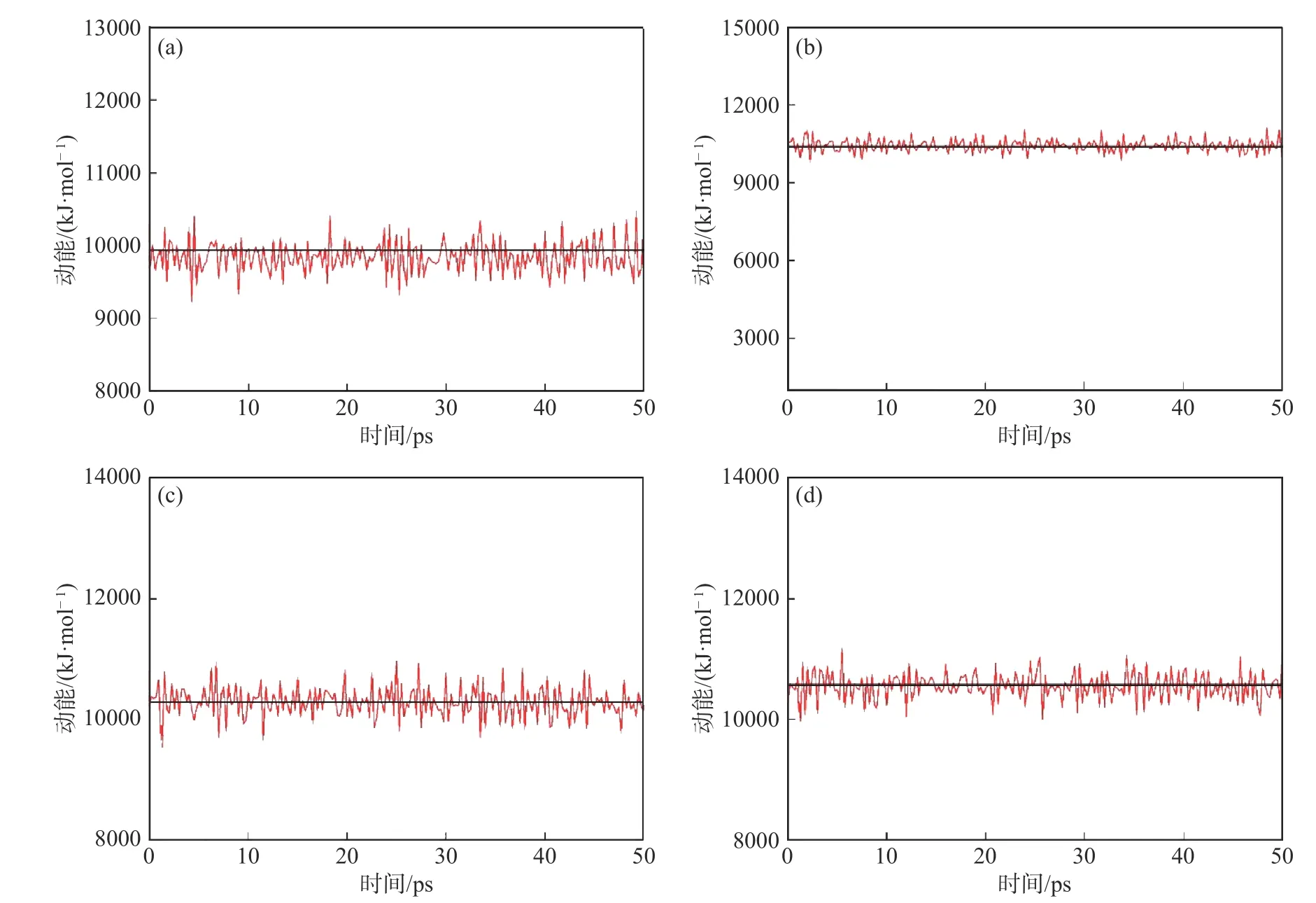
图5 芯材运动动能随时间的演化曲线.(a) Cr-MIL-101@十八酸;(b) Cr-MIL-101@十八胺;(c) Cr-MIL-101@十八醇;(d) Cr-MIL-101@十八烷Fig.5 Evolution curve of the kinetic energy of core materials with different time: (a) Cr-MIL-101@octadecanoic acid; (b) Cr-MIL-101@octadecylamine;(c) Cr-MIL-101@octadecanol; (d) Cr-MIL-101@octodecane
从图5可知,在经过一定时间后,芯材分子在金属有机骨架孔道内运动的动能逐步趋向于稳定,图中的黑色水平线给出了动能的平均值.十八酸分子和金属有机骨架基体之间有较强的相互作用,因而受到的束缚作用较强,表现为芯材分子运动的动能较低.十八胺、十八醇分子和金属有机骨架基体之间的相互作用低于十八酸分子,因此受到的束缚作用相对较弱,表现为芯材分子动能的提升.十八烷分子和金属有机骨架基体之间的相互作用最弱,但是受到“自发降低表面能”而带来的束缚作用,因而也未表现出很高的动能.芯材分子在金属有机骨架孔道内运动动能的模拟结果与上述的讨论一致,进一步证实了金属有机骨架基体与十八酸分子之间的相互作用最强,十八胺和十八醇分子次之,十八烷最弱.
2.5 金属有机骨架材料负载不同相变芯材下热容的分子动力学模拟
热容的模拟计算结果如表4所示,从表中可以看出,金属有机骨架负载十八胺和十八醇时热容较大,这与芯材在金属有机骨架孔道内受到的束缚作用较小有关.由于束缚作用较小,热运动更加剧烈,因此可以吸收更多的热量.对于十八酸和十八烷,由于芯材分子的运动较为受限,因此表现出相对较低的热容,这种趋势与上述模拟结果一致,证实了十八酸分子与金属有机骨架基体之间的相互作用较强,十八胺和十八醇次之,十八烷最弱.

表4 金属有机骨架材料负载不同相变芯材的热容Table 4 Heat capacity of MOFs loaded with different core materials
3 结论
(1)分子动力学研究表明十八酸和Cr-MIL-101之间的相互作用最强,十八醇和十八胺次之,十八烷最弱.
(2)十八酸分子和金属有机骨架基体之间的强相互作用产生一种拉伸作用,使得其回转半径最大,十八醇和十八胺次之,十八烷最小.
(3)十八酸分子和金属有机骨架材料之间相互作用较强,受到金属有机骨架的束缚作用,从而扩散系数较低,这种现象也发生在十八醇分子中;十八胺分子与金属有机骨架基体之间的相互作用较为适中,可以抵消二者间的相互作用,从而使得十八胺分子的运动较为自由,表现出较高的扩散系数;对十八烷分子而言,其与金属有机骨架之间相互作用较弱,因而分子间相互作用占据主导地位,在“表面能自发降低”的趋势下表现出团聚,不利于扩散的进行.此外,芯材分子在孔道内运动的动能与复合材料热容的模拟结果与这一结论相吻合.

