基于动态时间序列电压相关性分析的低压配电网拓扑校核

邹时容, 陆慧，洪梓铭，黄杰栋，陈琳韬，廖志伟

(1.广东电网有限责任公司广州供电局，广东 广州 510620；2.华南理工大学 电力学院，广东 广州 510641)

泛在电力物联网以电网为枢纽，将电力用户、电网企业、发电企业、供应商、电力客户、人及相关设备连接起来共享数据，为全行业和更多市场主体发展创造机遇和提供价值服务。电网正从设备管理模式向数据管理模式发生转型，电网的模型数据管理至关重要[1-3]。低压配电网结构复杂，缺乏技术手段进行网络拓扑异常检测及校验，大多依赖人工方式进行维护，导致更新不及时、数据质量较差，进而使得电力信息系统(如：营销管理系统、计量自动化系统、GIS系统、配电网生产系统等)中拓扑物理模型和信息模型及数据不匹配的问题较为突出；因而通过技术手段在运行过程对低压配电网的拓扑结构进行校核成为电力物联网的信息及数据共享必须解决的难点之一。

当前国内对低压配电网拓扑校核的研究大都集中于增加相应的智能设备。文献[4]提出利用智能分布式存储拓扑的信息进行拓扑识别；文献[5]提出利用智能终端单元借助通信网络查询局部拓扑信息，更新主站间的连接关系；文献[6]利用μPMU设备实现全网电压电流等数据的采样，从而实现拓扑识别的方式。

国外有学者提出了多种算法，利用已有的电网信息对拓扑结构进行校核，文献[7]利用电压谐波在1 d之内的变化规律，分析用户所处的拓扑位置;文献[8]基于主成分分析法的拓扑校核方法，对上送的负荷数据进行奇异值分解，达到降维的目的，从而得到电网的实际拓扑。通过算法识别网络拓扑可以很好地解决依靠物理设备带来的高费用及设备维护问题等，但对于数据的精确记录要求更高。

为确保泛在能源互联网各种配用电设备广泛互联、信息深度采集，近年来智能台区、宽带载波、5G等技术推广覆盖，使得智能电表采集大量海量数据[9](如：电量类、负荷类、事件类、电能质量及费控类等)的获取成为可能。多年积累的长时间尺度的电压、电流、功率时间序列信息为配电网拓扑分析奠定数据基础[10]。

本文以网络中电压序列具有相关性为理论基础，提出一种基于动态时间序列分割的电压相关性分析方法用于低压配电网的拓扑校核。

1 基于时间序列的电压相关性分析

1.1 电压相关性原理

电压相关性原理是指电流经过阻抗时产生电压降，系统阻抗两端相近点的电压曲线具有相似的波形序列。通过判断2个计量点之间电压变化曲线的相似性，即可判断两者在电气上的耦合程度。

图1、2为在不同的电气距离测点得出的电压分布图，横纵坐标为所分析2个计量点的电压，可明显得知：电气距离相近程度不同，其电压的数值分布和相关程度存在较大差异,其中图1耦合系数为0.916 5,而图2耦合系数为0.531 4。

常用欧式距离、动态时间规整(dynamic time warping，DTW)以及皮尔逊相关系数等作为定量衡量时间序列相关性的度量指标。欧式距离及DTW缺乏归一化的判断依据，需要进行数据的对比分析才能实现判断，而皮尔逊系数是归一化的相关判据。

1.2 皮尔逊相关系数

皮尔逊相关系数R(X,Y)是反映2个序列X、Y之间的线性相关程度的统计，其值介于-1到1之间，值的绝对值大小反映两者之间线性相关程度的强弱，绝对值越大两者的相关性越强，负号表示两者之间是负相关的关系，计算式为

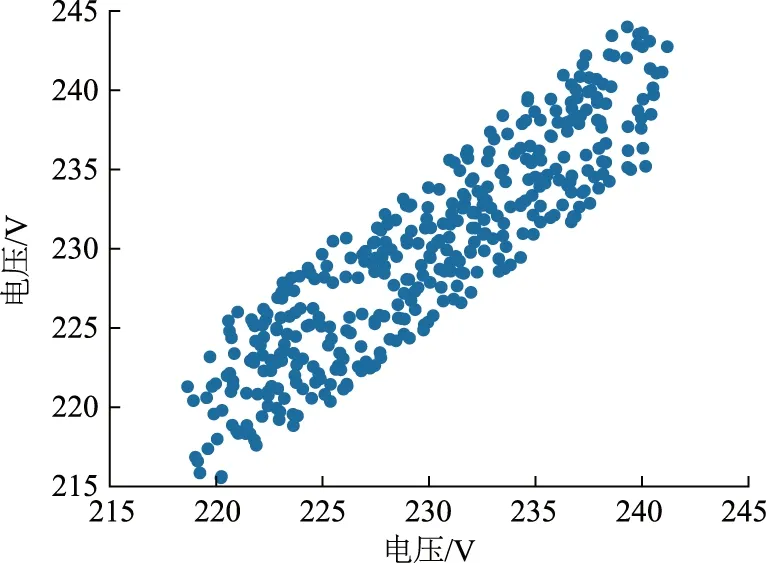
图1 高相关性

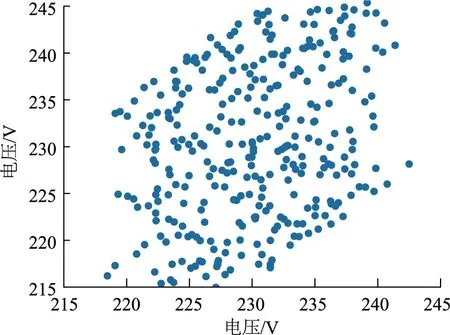
图2 低相关性

(1)

式中：cov(X,Y)为2个序列的协方差；σX、σY分别为序列X、Y的标准差。本文利用皮尔逊系数判断用户与台区之间连接正确是否。设定两者之间相关性强弱的阈值δ，若所得相关性R(X,Y)>δ，则说明两者之间在差异性较大处仍具有强的相关性，用户与台区之间具有正确的拓扑联系；若所得的R(X,Y)<δ，则说明两者之间的相关性关系较差，用户与台区之间拓扑结构连接关系存在错误，需要进行现场检验。

1.3 案例分析

本次案例分析使用的数据是某供电局中A、B、C 3个台区的电压数据，分析用户时以A的用户作为例子进行分析，判断这些用户与台区之间的电压关系。选择1月30日22：45至1月31日22：45的全部电压数据进行分析，由于采样器每15 min采样1次，共计每一相有96个数据点，包括3个台区配电变压器(简称“配变”)的电压数据，以及台区下所采集的20名用户的用电数据。皮尔逊相关系数的阈值可以根据不同用户类型进行设置，以提高分辨的正确率。

分析台区低压用户与配变电压数据的相关性，A台区用户电压曲线如图3所示。

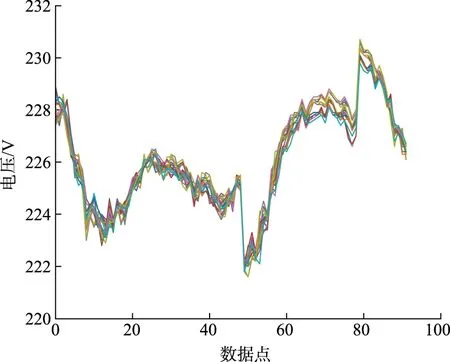
图3 A台区20个用户电压曲线

3个台区配变的三相电压曲线如图4所示。

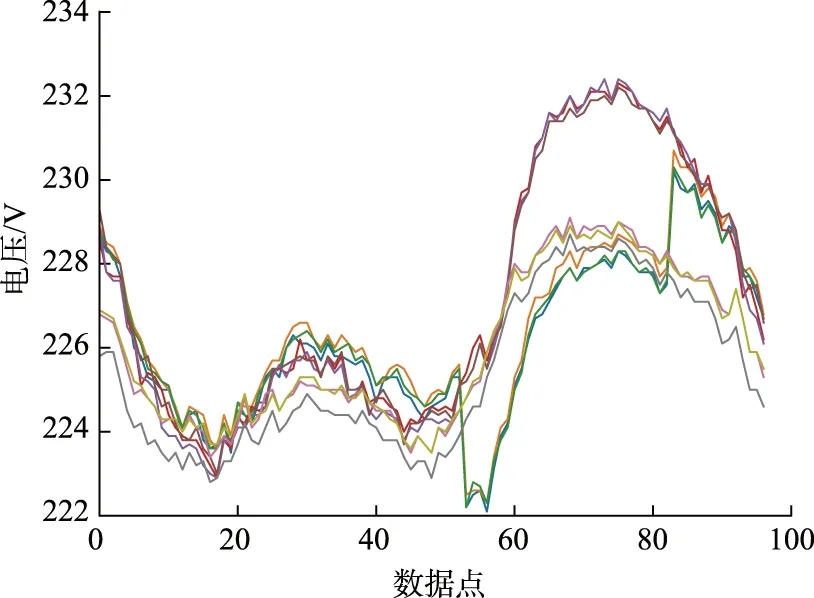
图4 3个台区变压器电压曲线

计算两者之间电压数据的相关性，结果见表1(表1中只给出部分用户)。

分析表1可知，用户与所连接的台区之间的电压相关性高于与其他台区之间的相关性，因此猜测设置相应的相关性的阈值可以作为验证用户与台区连接是否正确的依据。对此，检验由2月1日至2月27日共计60名用户与各台区之间的数据相关性系数，并对不同的相关系数阈值得出其准确率，结果见表2。

由表2可知：通过选择合理的相关系数阈值，可以判明其与所示台区的正确连接关系，提高阈值可以区分出用户与其连接不正确的台区，但是过高的阈值又可能导致将连接正确的台区误判为不正确；因此阈值的合理选择对判定结果的正确与否十分重要。

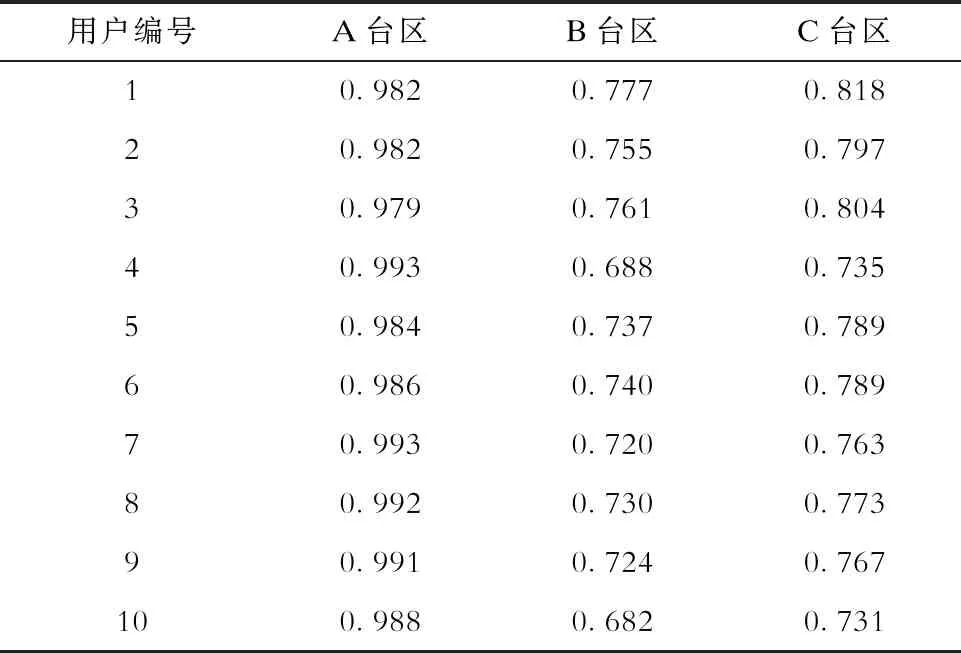
表1 用户与台区的相关性系数

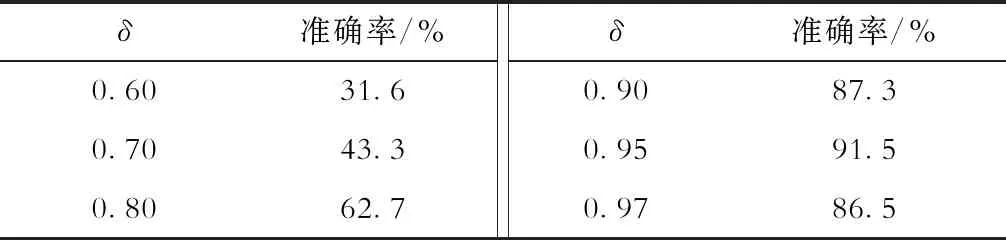
表2 阈值选择及准确率

本案例分析表明了利用相关性数据对用户与所连接台区进行识别校验的可行性，为后续的分析提供基本的理论依据。

2 时间序列分割

为提高拓扑校核准确度及快速性，有必要对用户电压时间序列进行分割，提取其中最能表征不同用户用电特征的子序列，进而研究台区与用户在该时间段内对应子序列之间的相关性。

目前常用的子序列分割方法主要有等长序列分割、滑动时间窗口分割和特定的序段分割算法等。

2.1 等长序列分割

对所取的一整段数据划分为长度为m的一系列序段。该分段方式简单，但对序列的信息分割不够完整，易造成子序列所含的信息紊乱并产生较大的误差。

2.2 滑动时间窗口分割

利用1个长度为m的时间窗口[11]在完整序列上滑动，得到n-m+1个子序列(n为完整序列长度)，该方法得到的子序列信息完整，但是数据量较大，计算过程复杂；同时在截取过程中，部分子序段所含信息不具研究价值；此外，长度m的选取，对于序段子序列的分析也具有重要的影响。

2.3 特定的序列分段算法

在时间序列当中，数据的变化趋势[12]、曲线斜率变化以及数据的极值点[13-14]等可以反映出数据的重要特征，体现数据中不同的局部特征；因此，以极值点或者曲率为序列子段划分的算法在序列划分中具有重要作用。

本文针对低压用户及台区配变之间的电压数据，利用极值点分段算法对数据进行分段并进行相关性研究，同时与滑动时间窗口的分析结果进行比较，检验所提算法对低压拓扑校核的有效性。

3 基于极值点的分段算法

在时间序列数据中，容易引起人为关注的通常为序列中的一些特征点，这些特征点往往能够表示序列的局部特征，反映出序列不同分段之间的趋势变化[15-20]。通过对时间序列的分段，可以去除无关序列的干扰，达到对时间序列的精确分析；为此，在这里提出利用极值点对序列的分段算法。

3.1 极值点的确定

假设有序列X={x1,x2,…,xc,…,xn},其长度为n，xc为X序列中的第c点序列项值。设k为c的领域，对c点进行如下判断：

a)若xc-k≤xc且xc≥xc+k，则判断为领域内的极大值点，用1表示。

b)若xc-k≥xc且xc≤xc+k，则判断为领域内的极小值点，用-1表示。

c)若不能够满足上述表达式，则判断该点在领域内不是极值点，用0表示。

3.2 序列特征点重要性标记

利用极值点判定算法对序列中的数据进行判定后，再应用重要性标记算法对序列中的每一个点判定其重要性标志等级，得到序列点的重要性标记序列TAG={t1,t2,…,tn}。设定其极值点的判断领域为K(整数)，在点i的领域范围内(i=1,2,3,…,n)，判断xi是否为极值，并更新TAG，具体流程如下：

a)初始化TAG，其中t1和tn为K，其余值为0。

b)对于k=1，判断TAG序列和原始时间序列X的每一个对应值是否满足如下判别式：①若ti=k-1且xi在其领域k内是极大值，则ti=ti+1；②若ti=-(k-1)且xi在其领域k内是极小值，则ti=ti-1；③若不满足上述的判定，则ti不变。

c)令k=k+1，返回步骤b)，直到k=K，并得到重要性标记序列TAG。

3.3 基于点重要性的序列分段

在序列TAG中，其值与原始时间序列X的值一一对应，表示在序列X中的点的重要性，其值越大相应的重要程度越高。利用点重要性的序列分段算法得到基于重要性的序列分段，分段方法如下：

a)输入TAG序列和原始时间序列X，在领域L内判断其分段，记录为CP。

b)对TAG序列中的每一个值ti,判断ti≥K或者ti≤-K;满足判定条件，则将xi记录为分段点，并得到有关序列分段点的CP序列。

4 算例分析

4.1 时间窗口分析

由图4可以发现：在大约50个数据点之后，3个台区的电压数据发生了比较大的变化；因此考虑以12 h作为1个时间段(即48个数据点)，研究在滑动时间窗口下，不同台区之间相关性系数的变化。为此提取3个台区变压器(2月1日至2月27日)由每天00:00至23:45的电压数据，利用时间窗口分析其相关性系数随时间段的变化,得到如图5所示的数个典型日的相关性变化曲线。

图5横坐标以00:00为基准，1个数据点为15 min。由图5可以看出：不同台区在夜间的电压数据其相关性系数可达到0.9以上；但随时间逐渐下降，大约在第30点(即07:00)过后各台区的相关性达到最低，然后又出现上升状态。

上述分析表明：低压用户与台区之间的连接关系可以由其电压的相关系数来阐明；同时，基于其相关性随每日时间序列的变化，对电压时间序列的分段分析是提高相关性分析过程准确率的一种有效手段。因用户电压序列与台区配变电压序列十分相似，下述将以台区配变电压序列相关性为例进行分析。

针对本案例所选的3个台区电压数据曲线(2月1日至2月27日)，将B、C台区与A台区电压数据进行相关性分析，相关性系数见表3。

图5 典型日相关性变化

由表3数据可知:根据设定的阈值，对于大部分的时间，序列分割时间法具有比较好的划分能力;但是仍有部分时间内，B、C台区与A台区电压数据的相关系数超过了阈值，这显然是不正确的；因此考虑利用序列分段的方法，提高区分的正确性。

利用时间窗口法分析2月每天的相关性变化，取出其相关性系数最低值以及其出现时间，结果见表4。

根据表4绘出其最小值出现时间的直方图如图6所示(左图表示B台区，右图为C台区)，其中以1 h作为时间的分段，可发现大部分的相关性最低点都出现在05:00往后的时间段。对每日的相关性系数进行比较得出：以05:00作为研究时段则其相关系数能保持在0.9之下，具有良好的辨识度；而对于该时段之前出现最小值的情况，进一步研究可发现其出现时间为国内节假日时期，可猜测节假日时期用户用电习惯与平时不同是导致其电压曲线出现差异的根本原因。

利用滑动时间窗口分析可有效地提高基于相关性在鉴别用户拓扑方面的能力，但是其运算时间长，对于拥有庞大用户数量的电网必然会出现计算量过大情况，而且时间长度选择的不科学，也可能致使信息的冗余。

表3 每日数据相关性系数表

表4 2月份相关性系数最小值表

图6 B、C台区最小相关系数出现时间直方图

4.2 时间序列分段算法分析

为解决利用滑动窗口分析时间过长的问题，利用极值点分段算法对时间序列进行分段分析，利用不同分段的相似性变化规律，提高相关性分析时的速度。选择A台区作为被比较台区，分析B、C台区与A台区之间的相关关系，分析结果见表5。

可见利用极值点分割算法同样能够区分序列中表现模式不同的分段，在一定程度上起到降低序列相关性，提高序列区分的能力。

与时间窗口分析法相比较，序列的分段分析同样可以取出序列中表现有差异的时间段，并且具有更快的分析速度，但在分析工程中，并未直接比较序列以提取序段；因此，在分析相关性的下降程度上不如应用滑动时间窗口分析法。

表5 相关性分段分析表

4.3 多种方式的分析速度比较

本次案例分析利用python语言编写，机器配置为3.6 GHz处理器、8 GB内存以及windows 10系统。利用均值求取分析使用不同方法27 d内计算相关性的耗时，结果见表6。

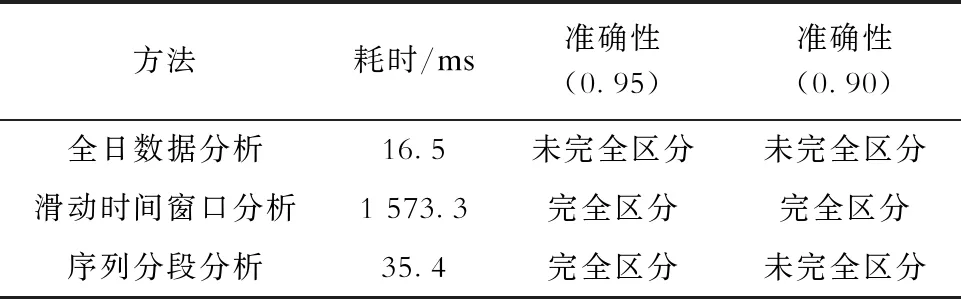
表6 不同方法计算时间

结合表3—6可知：相比较利用全日数据分析，时间序列分段分析在计算耗时上增加并不多，但能够起到有效提高区分过程准确性的作用；滑动时间窗口分析法在分析的准确性上是最高的，但其耗时是分段分析方法的50倍，对于拥有数百万用户的电网而言，其计算耗时太多，因而时间序列分段分析方法具有更好的应用前景。为了完善其阈值选择相对较高的缺陷，可设置双阈值检验，对于准确性在0.90至0.95之间可能存在误判的少数用户，利用判定阈值相对高的滑动时间窗口进行检验，则可以降低误判的可能性和减少使用计算资源。

5 结论

a)在低压配电网中，位于同一线路的配变以及低压用户的电压波形相近，利用皮尔逊系数可以判断在台区与低压用户之间的连接关系是否正确。

b)为了提高序列相似性计算过程的准确性，需要对序列进行分段；利用序列的趋势变化模式、曲率、极值点等均可以将序列分为多个子片段，其中极值点保留了用户变化信息，故其分段价值更大。

c)对比全日数据统计结果，利用滑动时间窗口和基于极值点序列分段方法均可以提高相似性识别的准确性，且具有更快的计算速度。