基于经验模态分解的彩虹法测量研究

罗道斌，秦毅盼，岳宗敏，骞来来，师 博，谢娇娇

（陕西科技大学 文理学院，陕西 西安 710021）

引言

折射率和直径是能表征微小粒子特性的重要参数，高精度测量微小粒子的折射率和直径有许多应用，如喷雾液滴蒸发、燃烧等过程的测量[1-2]。彩虹测量技术由于其非接触、高精度、快速、大信息量、可定量计算等优点，在测量微小粒子的折射率和直径中有广泛的应用[3-4]。随着彩虹技术的发展，小粒子的形状不再局限于球形，彩虹法同样适用于扁圆、椭球粒子的测量[5-7]。此外，彩虹技术也可测量液柱或液滴折射率梯度和温度梯度[8]，或测量喷雾场群粒子平均直径和平均折射率[9-10]。在提高彩虹测量精度方面，有许多研究在测量方法及计算方法的优化上。通过计算折射率或直径的微小变化量与彩虹Ripple 结构相位偏移之间的关系，可对折射率或直径的相对变化进行测量[11]；利用高阶彩虹条纹对于椭球度的敏感度非常高的特征，通过高阶彩虹可以更准确反演扁圆液滴的椭球度[12]；通过研究高斯光束入射下的彩虹分布规律，采用合适的高斯光束腰大小和光束位置可提高信号强度，提高反演精度[13]；结合最小二乘优化算法和彩虹技术反演算法，可对粒径分布及折射率实现高精度测量[14]。

经验模态分解(empirical mode decomposition,EMD)，是一种非线性、非平稳信号分解方法[15]。这种方法无须预设任何基函数，本质是通过数据的特征时间尺度或特征空间尺度，获得信号的本征波动模式，然后再分解数据，能将一个频率不规则的信号波分解为多个单一频率的波，和一个平均趋势项波的形式。广泛应用于分析非线性、非平稳信号序列[16-17]。本文结合经验模态分解方法与液滴一阶彩虹强度分布理论，研究了一种新的针对彩虹测量的反演算法，并用于液滴的折射率与直径的同时测量。本方法简化了测量过程，具有去噪声能力强、计算用时少，折射率与直径的测量精度高的特征。

1 彩虹技术原理

一阶彩虹强度分布主要包含Airy 结构和Ripple 结构，图1为折射率m=1.332 4，直径D=700 μm的一阶彩虹强度分布。理论和实验研究表明，彩虹强度分布与入射光波长、液滴折射率和液滴直径有关[18]。

图1 一阶彩虹散射强度分布Fig.1 Distribution of first-order rainbow scattering intensity

由几何光学理论，几何光学彩虹角θrg与折射率m之间的关系为

根据彩虹的Airy 理论，彩虹角附近散射光虚拟波前的波动方程为

式中z为无量纲参量，表示与彩虹角的归一化角偏差，可表示为

式中h为彩虹三次波前曲率，表示为

几何彩虹角位于z=0 处，由(2)、(3)式可求出几何彩虹角处的光强为最大光强（一级Airy 峰值）的43.93%。

根据彩虹Airy 理论，第一个Airy 峰的角位置与折射率和直径之间的关系表示为[19]

式中α为无量纲直径参量α=πD/λ。根据图2中的几何关系，彩虹Ripple 结构的频率FRipple，可通过计算对应于彩虹角时无限远处外反射光线与内反射光线的光程差获得[20]：

图2 彩虹Ripple 结构的形成原理Fig.2 The formation principle of rainbow Ripple structure

2 反演算法研究

2.1 彩虹信号的EMD 分析

EMD 是一种尺度分离算法，用I(θ)表示信号强度，首先确定I(θ)的所有极值点，再用三次样条曲线构造由极大值点组成的上包络线u(θ)和由极小值点组成的下包络线v(θ)，计算上下包络线均值序列：

求原信号序列I(θ)与均值序列p(θ)的差值序列：

通过判断q(θ)是否满足：1）极值点数量与过零点数量相等或最多只差一个；2）在任意点q(θ)的上下包络线均值为0。若满足则q(θ)为分解出的第一个高频本征模态函数(intrinsic mode function,IMF)，若不满足，对q(θ)重复取上下包络线均值序列，再计算差值序列，直至差值序列满足停止条件，满足停止条件的差值序列为分解出的第一个高频模态IMF1。用I(θ)减去IMF1，对剩余分量继续重复以上过程，直到分离出全部模态序列。信号最终可表示为

式中:IMFi(θ)表示第i个本征模态函数；R(θ)表示彩虹强度总体趋势。

图3为模拟m=1.332 4，D=700 μm 彩虹信号的EMD 分析结果，IMF1和IMF2代表彩虹的Ripple分量，IMF3代表彩虹的Airy 分量，最后一项R代表了彩虹信号的平均趋势。从EMD 分析结果中可有效分离Airy 分量和Ripple 分量，并可得到第一个Airy 峰的角位置θ1。

图3 彩虹信号经验模态分解Fig.3 EMD of rainbow signal

实测彩虹信号含有噪声，对同一液滴连续采集的2 帧彩虹信号做EMD 分析，求2 组EMD 结果对应模态间的互相关系数，由于噪声的随机性，代表噪声分量的对应模态不相关，代表彩虹有效分量的对应模态应高度相关，可由此判断彩虹信号的EMD 结果中的噪声模态，对彩虹信号进行去噪。互相关系数可表示为

式中：N为数据点个数；X和Y分别代表2帧采集数据的对应模态序列。当r＞0.8 时判定该模态高度相关，即该模态为有效信号；当r＜0.3 时，判定为不相关，即该模态为噪声分量。

为了验证上述去噪方法，理论模拟了m=1.332 4，D=700 μm 的液滴的一阶彩虹信号，并对该信号加上2 组随机噪声，得到2 组加了不同随机噪声的彩虹信号，如图4所示。

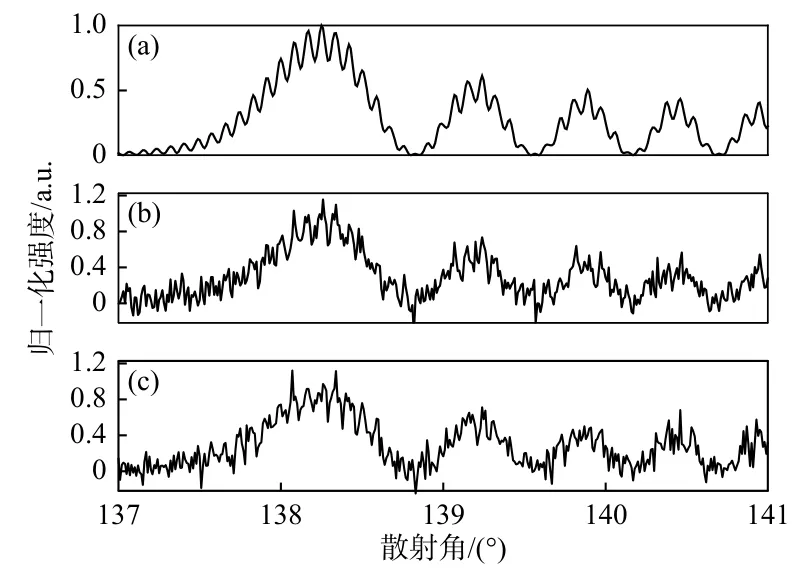
图4 彩虹信号Fig.4 Rainbow signal

图5为图4中2 组加入随机噪声后的彩虹信号的EMD 结果。2 组EMD 结果对应模态间的互相关系数计算结果如表1所示，由表1中数据分析，IMF1为噪声分量，IMF2和IMF3为Ripple 结构分量，IMF4为Airy 结构分量，R反映光强趋势。

图5 彩虹信号的经验模态分解结果Fig.5 EMD results of rainbow signal

表1 直径和折射率的修正结果Table1 The inversion results of diameter and refractive index

结合表1分析结果，对图5(a)加入随机噪声的彩虹信号减去IMF1，得到滤噪结果，滤噪结果与原信号相关系数为0.82，说明了彩虹信号EMD 去噪技术的有效性。

2.2 反演算法的设计

折射率在1.3～1.5，直径在100 μm～2 000 μm 范围内，根据彩虹分布在z=0 处强度与最大峰值强度间的关系，可通过在一级Airy 峰小角度侧搜索强度最接近最大强度的43.93%的角位置，代入(3)式，得到折射率初值m0。利用FRipple对折射率和直径的变化表现出的不同强度的变化规律将m0代入(6)式，得到直径D1。再由θ1对折射率和直径的变化表现出的不同强度的变化规律，将D1代入(5)式，得到折射率m1。通过反复将得到的折射率和直径分别代入(6)式和(5)式不断修正结果，再通过求解(11)式，得到多次修正结果的最优值。

式中：I0θ为实测彩虹信号；Ikθ为每组修正结果模拟的理论彩虹信号。

3 实验结果与分析

3.1 测量装置及测量方法

实验系统如图6所示。由注射泵（LINZ-8A，雷恩，上海）定量控制压出液体，悬挂在光纤末端形成球形液滴，由激光器（λ=632.8 nm，P=2 mW）发出的平行光束经平面镜反射后照射液滴，经液滴散射形成彩虹条纹，用CCD（SG-14-01k80-00-R，1 024像素）记录彩虹分布。显微相机（LP-530HS，倍特嘉，苏州）用来监控液滴和辅助测量。本实验在光学暗室进行，实验温度22.4 ℃。

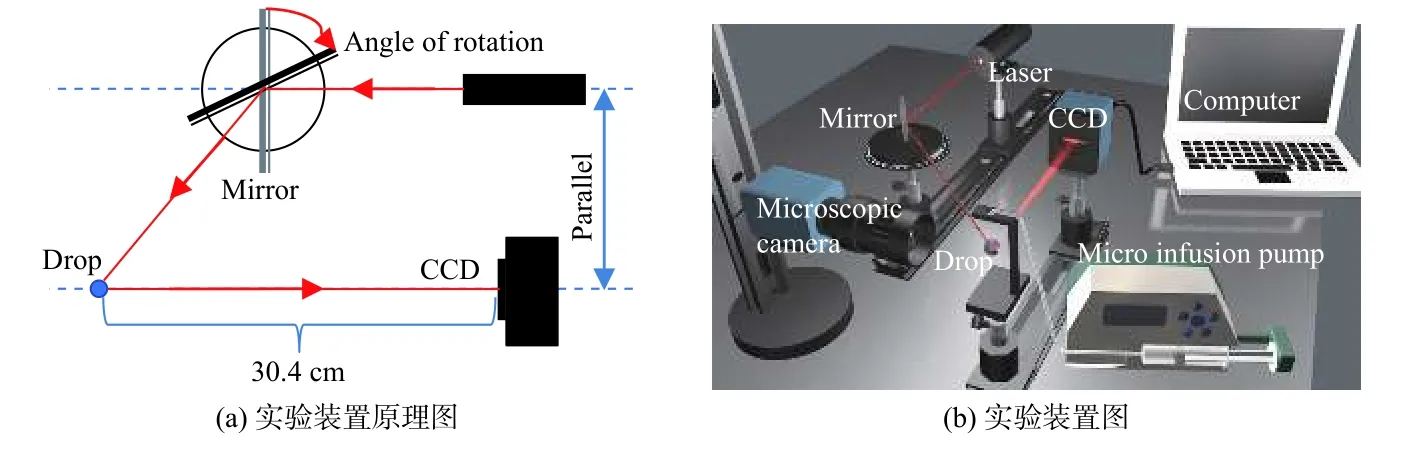
图6 实验装置图Fig.6 The experimental diagram

通过移动和旋转平面镜，角度精度为0.017°，使CCD 恰好能接收到一阶彩虹信号，旋转角度为φ，CCD 单个像素大小为14 μm，与液滴中心距离为30.4 cm，可确定CCD 测量角宽度Δθ=2.704°，由φ和Δθ可确定测量的散射角范围。CCD 每次采集512 帧数据。实验液滴样品为浓度0%～20%的乙醇溶液。

3.2 实验结果与分析

图7为实验中线阵CCD 和面阵CCD 采集的纯净水的一阶彩虹，图7(a)为线阵CCD 连续采集的512 帧彩虹分布；图7(b)为面阵CCD 采集的一阶彩虹分布。从同次采集的512 帧数据中取连续的2 帧数据，对2 帧数据进行EMD 分析，且对EMD 结果中对应模态间互相关系数进行计算，结果如表2所示，由表中数据分析，IMF1为噪声分量，IMF2、IMF3、IMF4为有用信号与噪声分量的混合信号，由于部分噪声频率接近Ripple 频率，噪声分量和信号分量会在同一个IMF上混叠，混叠信号只影响FFT 强度，不影响Ripple 频率。对原信号减去高频模态，得到Airy 分布，与原信号的对比如图8所示，从图中可以看出，滤波后的Airy 分量与原彩虹信号吻合。由Airy 分量得到θ1=138°，θrg=137.77°。对原信号去噪结果如图9所示。对去噪信号进行FFT，结果如图10 所示，得到FRipple=38.81。根据反演算法，折射率和直径的多次修正结果如表3所示。最后将修正结果代入(11)式得到最优结果为m=1.332 3，D=1 881 μm。液滴直径的参照值由显微相机确定为1 883 μm；由文献[21]可知，在该实验温度及632.8 nm 波长下，水的折射率为1.332 0，与实验反演结果吻合。

图7 一阶彩虹条纹图Fig.7 First-order rainbow distribution

表2 2 帧数据EMD 结果中对应模态间的互相关系数Table2 Correlation of two frames of measurement data

图8 EMD 滤波后的Airy 分量与原信号的对比Fig.8 Comparison between detected signal and signal filtered by EMD

图9 EMD 方法去噪后的彩虹信号图Fig.9 Rainbow signal after wave filtering by EMD

表4是不同浓度不同直径的乙醇液滴的测量结果与参照值的对比，折射率参照值由文献[22]给出，直径参照值为显微相机测量值。

图10 去噪后的彩虹信号频谱Fig.10 Frequency spectrum of rainbow signal after denoised

表3 直径和折射率的修正结果Table3 Inversion results of diameter and refractive index

表4 不同浓度乙醇液滴直径和折射率的反演结果Table4 Inversion results of diameter and refractive index

4 结论

本文基于经验模态分解法对彩虹信号分解和重构，结合一级Airy 峰的角位置和Ripple 结构与折射率、直径间的关系，设计了彩虹-经验模态分解算法对液滴的直径和折射率测量。利用相关运算，可快速分辨经验模态分解后的各个模态属性，能准确分离彩虹强度分布中Airy、Ripple 结构及噪声。实验测量了水滴和不同浓度乙醇液滴的一阶彩虹分布，并通过彩虹-经验模态分解法反演获得了液滴的直径和折射率信息。研究结果表明，折射率在1.3～1.5，直径在100 μm～2 000 μm，彩虹-经验模态分解法的折射率的测量精度达到10-4，直径的测量误差不超过1%。本研究的方法具有设计简单、计算用时少、测量结果可靠、适用范围更广、抗噪声强的特征。